常见空间距离的求解策略

■山东省嘉祥县第一中学 韩 阳

空间距离是立体几何研究的一类重要问题，也是高考的重点内容，主要包括点点距离、点线距离、点面距离、线线距离、线面距离、面面距离。其中以点到点的距离、点到线的距离、点到面的距离为基础，线面距离、面面距离都可以转化为点到面的距离。

一、定义法

根据已知条件，利用几何体的特征，结合空间距离的定义和立体几何的知识先证明某线段为所求的距离，然后再通过解三角形求出空间距离。

例1某几何体的三视图如图1所示，则该几何体的最大棱长为（ ）。

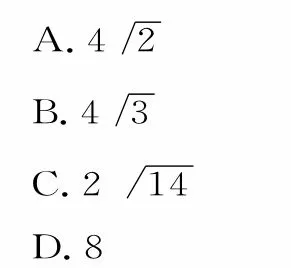
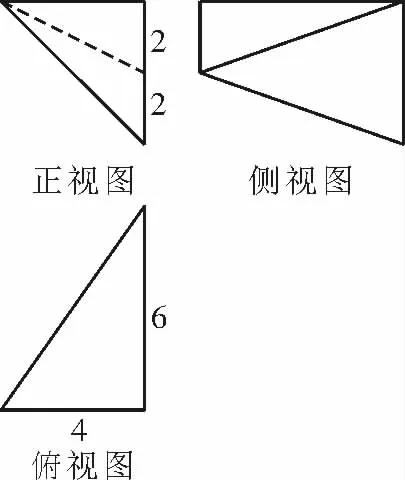
图1

解析：由题意可知该几何体的直观图是长方体的一部分，如图2 所示，所以该几何体的最大棱长为

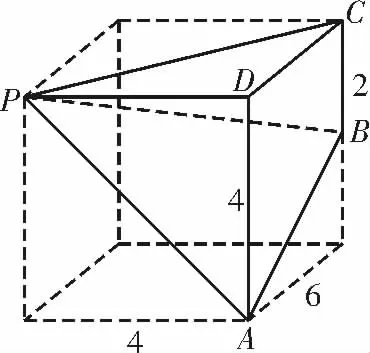
图2

点评：利用棱锥的定义，由三视图作出四棱锥的直观图，结合直观图利用匀股定理求相关几何量的数量，进而求出结果，解决此类问题的关键是由三视图还原出原来的几何体。

二、公式法

利用几何体的体积公式或表面积公式，直接计算出所求距离或线段的长度。

例2若正三棱柱的所有棱长均为a，其体积为16，则a=___。

解析：由题意得16，解得a=4。

点评：正三棱柱的底面为正三角形，侧棱垂直于底面，柱体的体积等于底面积乘以高，边长为a 的正三角形的面积为

三、等体积法

当点到平面的距离不易求时，可先构造一个三棱锥，若此三棱锥的底面积比较好求，且通过转化顶点，求出三棱锥的体积，再利用三棱锥体积的不变性，求出点到平面的距离。

例3边长为2的正方形ABCD 沿对角线AC折叠，使得△ACD 垂直于底面ABC，如图3所示，则点C 到平面ABD 的距离为（ ）。

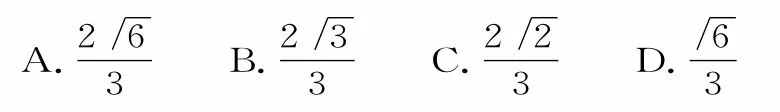
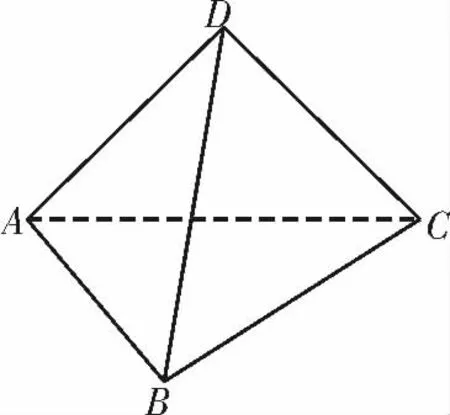
图3

解析：如图4，取AC的中点O，连接DO 和BO，则DO⊥AC，BO⊥AC。

由于四边形ABCD 是边长为2 的正方形，所以AD=CD=AB=BC=2，则

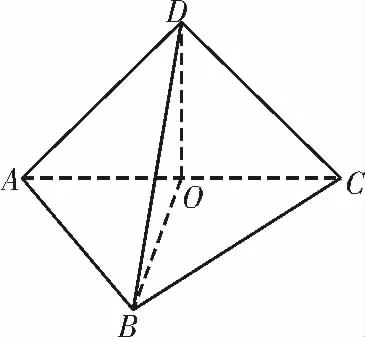
图4

由题知，平面ACD⊥平面ABC，且交线为AC，而DO ⊂平面ACD，则DO ⊥平面ABC。

又BO⊂平面ABC，所以DO⊥BO，所以在Rt△BOD 中

所以△ABD 是等边三角形，则S△ABD=

点评：本题利用等体积法求出点到平面的距离，避免了从点C 作平面ABD 的垂线，体现了转化与化归的思想，起到了化繁为简的效果。

四、向量法

如果由题意可以比较容易地建立空间直角坐标系，则可以使用向量法处理空间距离问题，关键是坐标要正确，运算的过程要准确。如果是不易直接建系，当知道长度与角度时，可以考虑使用非坐标形式下的向量运算进行求解。

例4如图5，在四棱锥P-ABCD 中，底面ABCD 是一个直角梯形，其中∠BAD=90°，AB∥DC，PA⊥平面ABCD，AB=AD=PA=2，DC=1，M 和N 分别为PA 和PC 的中点。

（1）求点P 到平面DBN的距离；

（2）设点N 在平面BDM内的射影为点H，求线段HA 的长。

解析：（1）在四棱锥P-ABCD 中，底面ABCD 是一个直角梯形，∠BAD=90°，PA⊥平面ABCD。

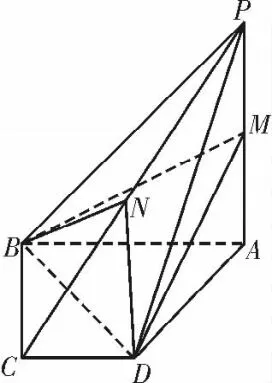
图5

所以以A 为坐标原点，AB，AD，AP 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，如图6，则D（0，2，0），M（0，0，1），P（0，0，2），B（2，0，0），

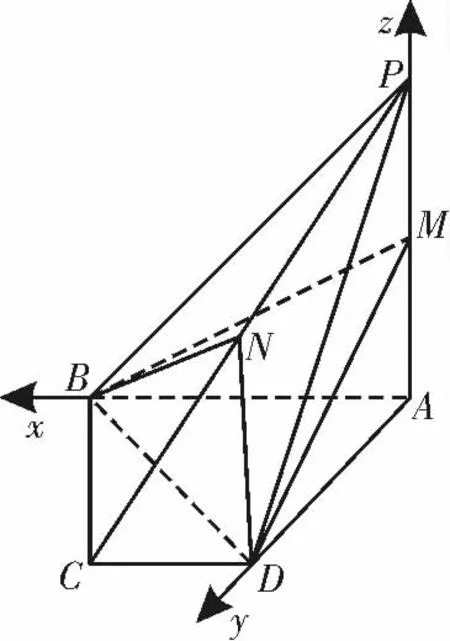
图6

设平面BDN 的法向量为m=（x1，y1，z1），则取x1=1，得

设平面BDM 的法向量为n= （x2，y2，z2），则取x2=1，得n=（1，1，2）。

（2）设点N 在平面BDM 内的射影为点H（a，b，c），则所以点N 到平面BDM 的距离为d2=

点评：利用向量法解决空间距离问题常用到下面两个结论：（1）点到直线的距离：设过点P 的直线l的方向向量为单位向量n，A为直线l外一点，点A 到直线l 的距离d=（2）点到平面的距离：设P 为平面α 内的一点，n 为平面α 的法向量，A 为平面α 外一点，点A 到平面α 的距离