立体几何易错点透视

■山东省沂南县第二中学 贺小兵

本文通过对立体几何中常见的易错题进行归纳总结，结合立体几何中几类典型问题进行分析，帮助同学们纠正错误认识，提高正确解题能力。

考向1:线线、线面、面面关系

空间中线线、线面、面面关系是立体几何的核心内容，其中又以线面的平行与面面的垂直问题为重点。

例1如图1，四边形ABCD 是平行四边形，平面AED ⊥平面ABCD，EF∥AB，AB=2，BC=EF=1，AE =，DE=3，∠BAD=60°，G 为BC 的中点。求证：平面BED⊥平面AED。

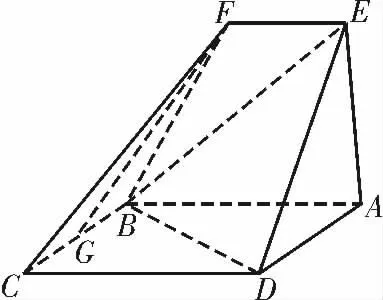
图1

证明：在△ABD 中，AD=1，AB=2，∠BAD=60°，由余弦定理得BD =，进而可得∠ADB=90°，即BD ⊥AD。又因为平面AED⊥平面ABCD，BD⊂平面AED，平面AED∩平面ABCD=AD，所以BD ⊥平面AED。又因为BD⊂平面BED，所以平面BED⊥平面AED。

易错点分析：本题易出错的原因：一是BD⊥AD 没有给出确切的证明过程，同学们在证明线线垂直时，易忽略利用余弦定理或勾股定理，求三角形边长之间的关系；二是书写格式不规范，对于线面垂直、面面垂直判定定理的使用，关键点不写出，例如，本题中的平面AED∩平面ABCD=AD 没有写，导致过程分拿不到。

小结：同学们要掌握线线垂直、线面垂直、面面垂直之间的相互转化。熟练掌握线面平行、面面垂直的判定和性质是迅速解题的关键。

考向2:空间角

从近几年高考全国Ⅰ卷理科命题趋势来看，立体几何解答题第一问通常考查线线、线面、面面关系，第二问通常考查空间角，即异面直线所成的角、直线与平面所成的角、平面与平面所成的角。

例2如图2，四边形ABCD 为菱形，∠ABC=120°，E，F 是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC。

（1）证明：平面AEC⊥平面AFC；

（2）求直线AE 与直线CF 所成角的余弦值。

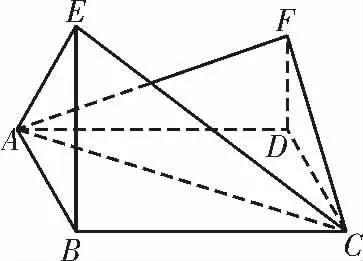
图2

解析：（1）如图3，连接BD，交AC 于G，连接GE，GF。在菱形ABCD 中，有AC⊥BD。不妨设GB=1，又∠ABC=120°，可得AG。又AE ⊥EC，所以

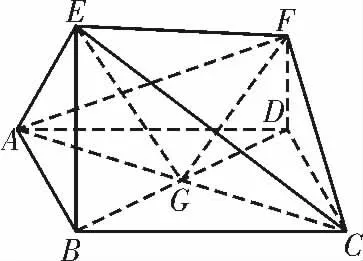
图3

因为BE⊥平面ABCD，所以BE⊥AC，因为AC⊥BG，BE∩BG=B，所以AC⊥平面BEG，所以AC ⊥GE。同理可证AC ⊥GF，所以∠EGF 是二面角E-AC-F 的平面角。在直角梯形FDBE 中，EF2=BD2+所以GE⊥GF。所以二面角E-AC-F 的平面角为90°，故平面AEC⊥平面AFC。

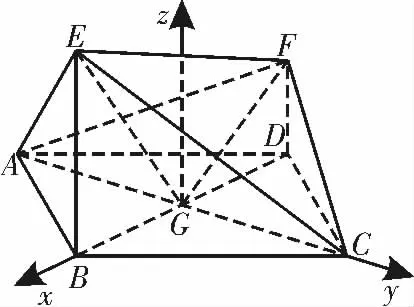
图4

易错点分析：证明面面垂直可转化为二面角E-AC-F 的平面角为直角或者是两个平面的法向量互相垂直。本题易出错的原因：一是利用传统方法，找不到二面角的平面角；二是利用向量法，不能建立合适的空间直角坐标系；三是忽略两条直线的夹角的取值范围是

小结：掌握求二面角大小传统方法的关键是作出二面角的平面角，然后构造三角形求解，即“一作二证三求”。向量法需利用空间直角坐标系，求两个平面的法向量的夹角，再判断其与二面角的平面角的关系。求空间线线角的传统方法是将相关的线进行适当的平移转化到同一个三角形中求解，关键在于平移空间的直线。向量法需利用空间直角坐标系，求两直线的方向向量的夹角，再判断其与直线夹角的关系。

考向3：空间距离的向量求法

例3如图5，四棱锥F-ABCD 的底面ABCD 是菱形，其对角线AC=2，BD =，AE，CF 都与平面ABCD 垂直，AE=1，CF=2。求点E 到平面ABF的距离。

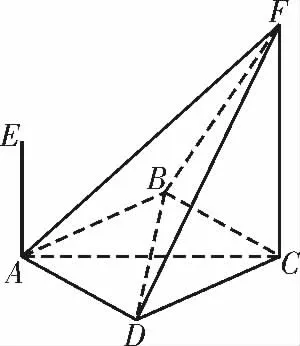
图5

解析：以A 为坐标原点，的方向分别为y 轴，z 轴的正方向，建立如图6所示的空间直角坐标系A-xyz，则F（0，2，2）。

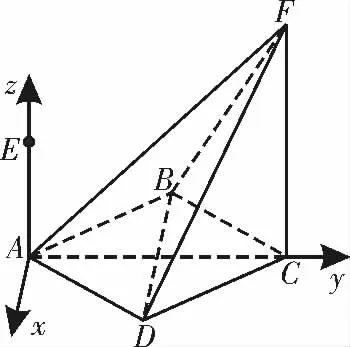
图6

小结：求点面距离的传统方法是构造直角三角形求解，其关键又是面的垂线问题。对于图形中含有垂直关系的点面距离问题，可通过建立空间直角坐标系，利用点到面的距离公式求解。还可以用“等体积法”求出点到面的距离。

考向4:平面图形折成立体图形，立体图形展开成平面图形

例4正△ABC 的边长为a，将它沿平行于BC 的线段PQ 折起（其中P 在AB边上，Q 在AC 边上），使平面APQ ⊥平面BPQC。若折叠后，A，B 两点间的距离为d，求d 的最小值。

解析：如图7，作AD ⊥PQ 于D，则D 为PQ 的中点。因为平面APQ ⊥平面BPQC，则 AD ⊥ 平面PBCQ。连接BD，则d2=AD2+BD2。设AD=x，则（E 为BC 的中点），于是因此

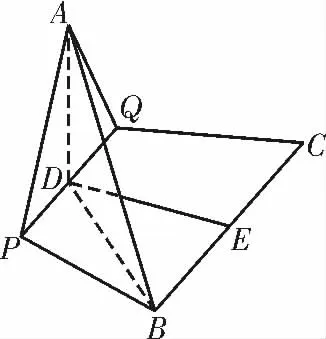
图7

易错点分析：该题考查同学们的作图能力，解题的关键是能根据折叠前后的位置关系与数量关系，列出AB 的表达式。希望同学们能在平时的学习中多加训练自己的空间想象能力和运算求解能力。

小结：解决此类折叠问题，需要明确哪些量变了，哪些量不变，然后根据题目中相关的数量关系，列出表达式，同时利用函数的性质，求出最值。所以当