立体几何中翻折问题的处理策略
2021-02-07河南省平顶山市第一高级中学
■河南省平顶山市第一高级中学 肜 彬
立体几何是高中数学的重点内容,图像的翻折是立体问题中的一类典型问题,是连接平面几何与空间几何的纽带,成为立体几何中考查分析能力与创新能力的好素材,备受命题者的青睐。立体几何翻折问题是指将平面图形沿着平面图形中的某条或几条线段将平面图形翻折,使之变成空间几何体,以此为载体,考查空间中点、线、面之间的相互关系,或角度与距离关系。现将翻折问题中的几类常见题型进行剖析,以其对同学们的复习备考能有所帮助。
一、翻折后位置关系的判定
例1如图1,在直角梯形ABCD 中,BC⊥CD,AE⊥DC,且E为CD 的中点,M,N 分别是AD,BE 的中点,现将△ADE 沿AE 所 在 的 直线折起,则下列说法正确的是___。(写出所有正确说法的序号)
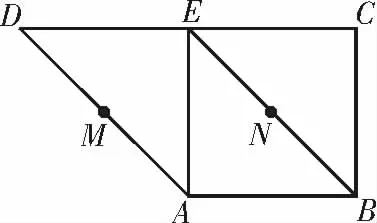
图1
①不论D 折至何位置(不在平面ABC内),都有MN∥平面DEC;
②不论D 折至何位置(不在平面ABC内),都有MN⊥AE;
③不论D 折至何位置(不在平面ABC内),都有AB∥MN;
④在折起过程中,一定存在某个位置,使EC⊥AD。
解析:由已知,在未折叠的原直角梯形中,AB∥DE,BE∥AD,所以四边形ABED 为平行四边形,所以BE=AD,折叠后如图2 所示。
①过点M 作MP∥DE,交AE 于点P,连接NP。因为M,N分别是AD,BE 的中点,所以P为AE 的中点,故NP∥EC。又MP∩NP=P,DE∩EC=E,所以平面MNP∥平面DEC,故MN∥平面DEC,①正确。
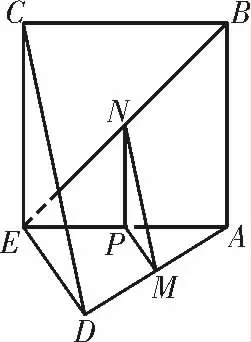
图2
②由已知,AE ⊥ED,AE ⊥EC,所以AE⊥MP,AE⊥NP。又MP∩NP=P,所以AE⊥平面MNP。又MN ⊂平面MNP,所以MN⊥AE,②正确。
③假设MN∥AB,则MN 与AB 确定平面MNBA,从而BE⊂平面MNBA,AD⊂平面MNBA,与BE 和AD 是异面直线矛盾,③错误。
④当EC⊥ED 时,EC⊥AD。因为EC⊥EA,EC⊥ED,EA∩ED=E,所以EC⊥平面AED。因为AD⊂平面ADE,所以AD⊥EC,④正确。
综上,说法正确的是①②④。
点评:解题的前提和必要步骤是分析清楚翻折前平面图形的结构特征,以及翻折前后图形中变与不变的量,特别要注意不变中的直角。
二、翻折后角度的计算
例2如图3,在四边形ABCD 中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E,F 分别在BC,AD 上,且E 为BC 的中点,现将四边形ABEF 沿EF 所在的直线折起,使二面角A-EF-D 的大小为60°,如图4,求直线AF 和平面ACD 所成角的正弦值。
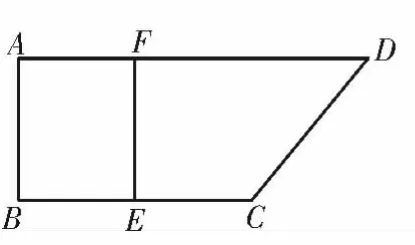
图3
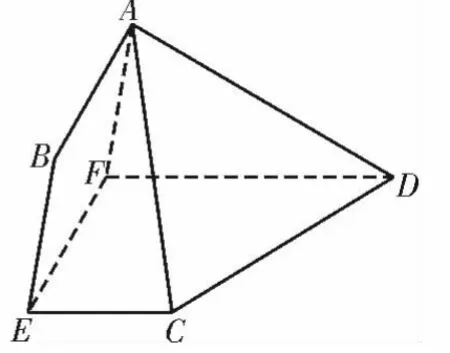
图4
解析:由已知可知,折叠后仍有EF ⊥AF,EF⊥FD,AF∩FD=F,则EF⊥平面AFD,所以∠AFD 为二面角A-EF-D 的平面角,即∠AFD=60°。
如图5,过点A 作AO⊥FD 于点O,因为AO ⊥EF,所 以AO ⊥平面CDFE。
过点O 作OM ⊥CD,垂足为M,连接AM,由三垂线定理得AM ⊥CD,所以CD⊥平面AOM,过点O 作ON ⊥AM 于点N,则ON⊥CD,所以ON ⊥平面ACD,即ON为点O 到平面ACD 的距离。
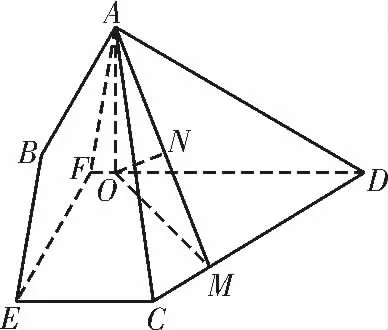
图5
点评:翻折后首先要确定线段的长度与角度中不变的量,再计算变化的量,其次确定关键点A 的位置,也就确定了点A 在底面上的投影,从而翻折后形成的空间图形的结构也就确定了,这样就可方便以后的计算与证明。
三、翻折后距离的计算
例3如图6,已知正方形ABCD 的边长为2,E,F 分别为AB,CD 的中点,将△DEA 沿DE 所在的直线折起,使得点A在平面DCBE 上的投影落在直线EF 上,如图7,求点C 到平面ADE 的距离。
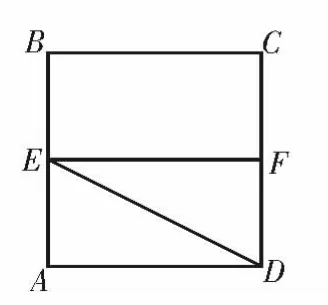
图6
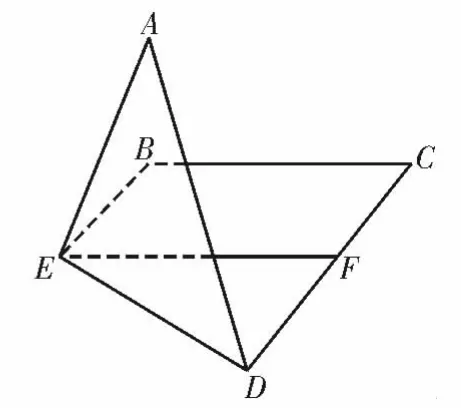
图7
解析:如图8,在正方形ABCD 中,设M为BC 的中点,连接AM 分别交EF,ED 于点N,G,由 Rt△AED ≌Rt△BMA,得∠AEG+∠EAG=∠AEG+∠ADE=90°,即AM ⊥ED。
在 图9 中,AG ⊥DE,MG ⊥DE,因 为AG∩MG=G,所以ED ⊥平面AGM,所以平面DCBE⊥平面AGM,所以点A 在平面DCBE 上的投影落在直线GM 上,由题设可知点A 在平面DCBE 上的投影落在直线EF上,所以点A 在平面DCBE 上的投影落在直线GM 与EF 的交点上,即点N。
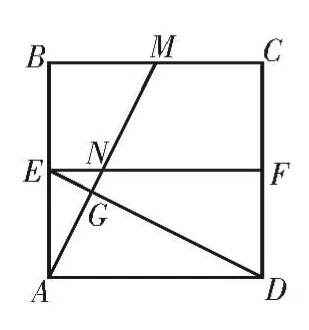
图8
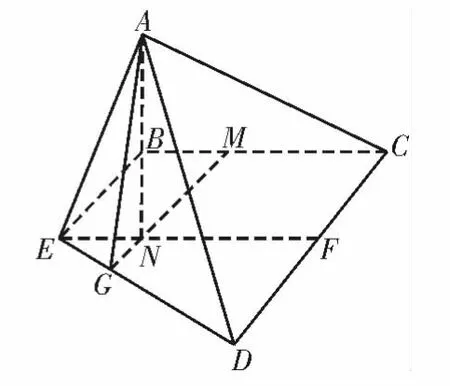
图9
点评:处理翻折问题时,一定要将翻折前后的图形相对照进行分析,找准翻折前后中的不变量,弄清哪些要在原平面图形中进行计算,哪些要在翻折后的立体图形中进行计算,这是处理翻折问题的一般性方法。
立体几何解题的根本思想是把空间问题转化为平面问题,解决翻折问题时,首先要根据题目的要求正确画出由平面图形折成的空间图形,即由平面图形转化成空间图形。在解题过程中,往往根据问题的需要再把空间图形还原成平面图形,对比平面图形和空间图形,找准翻折的起点与翻折的程度,弄清翻折过程中的变与不变的量进行求解,这是处理翻折问题的关键。
