深度卷积神经网络在滑动轴承转子轴心轨迹识别中的应用

郭明军, 李伟光, 杨期江, 赵学智

(1.华南理工大学 机械与汽车工程学院，广州 510640；2.广州航海学院 轮机工程学院，广州 510725)

转子系统是风机、汽轮机、轧机、压缩机等旋转机械中用于传递运动与动力的关键部件，其工作性能通常对旋转机械的稳定性和可靠性起决定性作用[1]。旋转机械高速重载的工作环境经常会使得转子系统产生振动，而剧烈的振动必须加以控制，否则将会使得机械零部件受损、引发机器故障，甚至造成严重的安全事故[2]。因此，研究转子系统状态监测与故障诊断方法对保持旋转机械的运行性能及使用寿命具有重要意义。

轴心轨迹是旋转机械振动信号的一种重要表现形式，包含了设备运行状态的丰富信息，它的特征提取与识别是旋转机械智能诊断的重要手段，本质上是二维图形的模式识别问题[3]。轴心轨迹的主要特征包括傅里叶描述子、几何参数特征及矩特征等，将这些特征与故障类型相对应，通过学习训练后，利用模糊聚类、灰色关联分析、支持向量机与人工神经网络等分类器实现故障的分类识别。李辉等[4]利用模糊C-均值聚类方法对轴心轨迹的多重分形谱特征进行了分类识别，取得了良好的效果。李友平等[5]以不变矩作为特征向量，采用关联度分析方法实现轴心轨迹的自动识别。万鹏等[6]提出了一种集成非线性流形学习和支持向量机相结合的故障诊断模型，应用于试验台转子系统故障识别，取得了较高的精度。郭鹏程等[7]采用边缘矩和粒子群来寻找关键故障特征，解决了轮廓的完整性和轮廓提取算法的稳定性问题，然后应用加权神经网络实现了4种典型轴心轨迹的识别。

上述传统智能识别方法虽然已在多个领域取得了成功，但它们将人工特征提取与分类识别两个紧密联系的过程分割为相互独立的两部分，步骤繁琐且无法适应复杂多变的实际环境。而近年来，Hinton等[8]科学家提出的深度学习因其具有较深的结构而具有强大的自适应特征学习能力，是解决上述问题的重要方法。在机械故障诊断领域，堆栈去噪自编码机(Stacked Denoising Auto-encoder, SDAE)、深度置信网络(Deep Belief Network, DBN)、卷积神经网络(CNN)等都取得了不错的效果。李松柏等[9]提出了一种集成多传感器信息及SDAE的齿轮故障诊断模型，具有比传统故障诊断方法更高的抗噪性及鲁棒性。李巍华等[10]利用DBN对轴承的原始振动信号进行自适应特征提取，增强了识别过程的智能性。刘星辰等[11]采用随机破坏输入和全局平均化策略对经典卷积神经网络模型LeNet-5进行改进，提出一种具有实时抗噪性能的一维卷积神经网络模型，实现了对原始轴承及齿轮箱振动信号的自适应特征学习与故障诊断。尽管深度学习已经在旋转机械故障诊断上取得成功，但在轴心轨迹的识别上的应用尚不多见。

本文针对轴心轨迹的识别问题，借鉴CNN在门牌识别、车牌识别及花卉识别等领域的成功应用,利用CNN所特有的卷积与池化结构，并结合样本数据的特点，提出一种深度卷积神经网络故障诊断模型DCNN-FDM用于轴心轨迹识别，并通过全连接层的主成分分析验证所提方法在特征学习方面的有效性。与传统方法(BP神经网络、Hu矩+BP神经网络以及Hu矩+SVM)相比，本文所提模型的识别效果更好，可实现转子故障的精确诊断。

1 CNN的工作原理

CNN是广泛应用的深度学习模型之一，具有与传统人工神经网络类似的层级结构，通常由输入层、卷积层、池化层及输出层等部分组成。其核心模块是卷积层和池化层，正是通过交替的卷积与池化操作，达到对输入数据特征的逐层剥离以期挖掘数据潜藏的更加抽象的特征。输出层通常采用softmax分类器，它是logistic回归模型在多分类问题上的推广，可用于输入数据的多分类任务当中。本节将重点介绍卷积、池化及softmax分类器的基本原理。

1.1 卷积运算

卷积层的作用是对输入数据的特征进行自适应提取，而这是通过每一个神经元固定的卷积核矩阵与上一层的输出特征矢量进行卷积运算来实现的。卷积的结果代表所提取的特征，每一个卷积核通过权值共享机制学习到输入的一类特征，即特征图(Feature Map，FM)。卷积过程可由下式描述：

(1)

式中：l为卷积核序号，Cl为CNN的第l层FM,a为卷积层输入，b为卷积核的偏置项，x、y、z分别为输入数据的不同维度。

为了能够提取到复杂的非线性特征，在卷积操作之后通常会引入激活函数来增加模型的非线性。ReLu激活函数因其特有的单边抑制特性，能够对深度学习模型进行稀疏后更好地挖掘相关特征，且收敛速度优于sigmoid和tanh函数，而被广泛应用。其原理为：

Hl=f(Cl)=max{0,Cl}，l=1,2,…,q

(2)

式中：Hl为Cl的激活值。

1.2 池化原理

卷积层之后是池化层(也称下采样层)，其作用是压缩数据及参数量，从而减小过拟合风险[12]。常用的池化策略有L2范数池化、平均池化和最大值池化，其中最大值池化应用最广，其表达式为：

Gl=downsamp(Hl)=maxHl(v1,v2)

(3)

式中：(v1,v2)为对上一层进行池化的元素尺度。

1.3 softmax分类器

通过交替的卷积层与池化层之后，需要通过全连接层将最后一个池化层的特征整合为一维的列向量xl,与输出最层的标签连接，最后由softmax完成分类任务。对于m类的多分类问题，softmax的输出可表示为[13]：

(4)

式中：θi(1≤i≤m)为模型的参数，f(θix)为模型的输出。

2 深度卷积神经网络故障诊断模型DCNN-FDM

CNN已经在手写字体识别、门牌识别等多个领域得到应用，鉴于本文研究的轴心轨迹识别与手写字体识别具有颇多相似之处，故可针对其特征来调整CNN的网络参数以实现轴心轨迹的自动识别。

2.1 DCNN-FDM的结构

本节采用的深度卷积神经网络故障诊断模型DCNN-FDM如图1所示，由图可知，该模型包括三部分：输入模块、特征提取模块和分类模块。

图1 DCNN-FDM模型

输入模块：输入图像通常为包含红黄蓝3原色的3通道图像且其尺寸大小不一致，为处理方便，需将其进行预处理为统一的尺寸大小，而这是由输入模块来完成的。图像预处理过程包括读取图像、二值化处理和最近邻插值三个步骤：首先，调用计算机视觉库(Open Source Computer Vision Library，OPENCV)中的cv2.imread()函数来读取原始图像；然后，调用cv2.threshold()函数将图像处理为灰度图；最后，调用cv2.resize()函数，采用最近邻插值算法，将图像尺寸统一缩放为32×32。

特征提取模块：该模块由两组交替的卷积层和池化层组成。卷积层通过多个卷积核可以提取到图像不同的局部特征，然后通过Relu激活函数对所得特征进行非线性映射，起到特征增强的作用。而池化层采用最大值池化，可以对输入数据进一步压缩及减少参数量，起到减少计算量和防止过拟合的作用。特征提取模块正是通过交替的卷积和池化层来实现轴心轨迹特征的自适应提取功能。

输出模块：输出模块由全连接层和softmax分类器组成。其中全连接层负责将特征提取模块中提取到的特征进行扁平化处理为一维的张量，然后再输入softmax分类器中得到各类输入的概率值。

经过反复试验，确定的网络参数如下：卷积核大小为5×5,移动步长为1；采用最大值池化，尺寸为2×2,步长为2；图1中64@28×28代表特征图大小为28×28，深度为64；全连接层神经元个数为1 024。

2.2 DCNN-FDM的训练

CNN的训练属于有监督训练，每个样本对应的输出与实际标签之间的差值定义为误差，模型训练的目的就是使得误差尽可能小。因此，模型训练最终可归结为一个优化问题。本文以交叉熵为损失函数，表达式为：

(5)

式中：x为输入特征,y为模型的实际标签，y_为模型的输出结果,即softmax的分类结果。

模型训练分为前向迭代求解和误差反向传播两个阶段。前向传播过程如下式：

(6)

反向传播过程采用梯度下降方法更新参数，输出层t的残差δt定义为

(7)

式中：∘表示逐点卷积。此时，容易得到权值W和偏置项b的梯度如下

(8)

对于最大值池化层，要从压缩过的输出层误差δt还原成池化前的大小，需要进行上采样，将第l-1层中最大值所对应的位置用第l层中的残差替代，而其余位置进行补零操作。即有：

δl-1=upsample(δl)∘f′(zl-1)

(9)

式中:upsample(.)表示上采样操作。

对于卷积层，则有：

δl-1=δl*rot 180(Wl)⊙f′(zl-1)

(10)

式中:*表示卷积，⊙表示向量内积，rot180表示对卷积核旋转180°。

通过上述方法，利用链式法则，可以求出各层的梯度，进而实现权重与偏置等网络参数的更新。

3 旋转机械实测轴心轨迹识别试验

试验装置为课题组自主研发的大型滑动轴承试验台，如图2所示，主要由大小减振平台、伺服电机、卸荷座、联轴器、转子及其左右两端的支承滑动轴承(宽径比0.75、间隙比0.002)和推力装置组成。试验中涉及的基本参数，如表1所示。

图2 滑动轴承试验台

表1 试验基本参数

本文监测的对象为图2中的转子，所用的传感器型号为KamanKD2306-1S、分辨率为0.01%FS、量程为0～2.5 mm。通过转子轴心轨迹的不同形状可以识别其对应的故障类型，两者的对应关系如表2所示。轴心轨迹的识别流程，如图3所示。

表2 轴心轨迹数据集

图3 轴心轨迹识别流程图

3.1 轴心轨迹提纯

转子的轴心轨迹可利用在转子同一轴截面两侧互相垂直的位置布置的两个位移传感器测得的信号D1和D2来合成，结果如图4所示。

图4 原始轴心轨迹

由图4可知，轴心轨迹混成一团而无法识别其本来面貌。这是由于设备结构及其运行环境的复杂性，引起实测的振动信号受到诸多干扰因素的影响，从而使得轴心轨迹杂乱无章。故在进行轴心轨迹识别试验之前，需要对测试的轴心轨迹进行降噪提纯。本文采用奇异值分解(Singular Value Decomposition, SVD)及其差分谱理论[14-15]，进行轴心轨迹提纯。图5为2 250 r/min转速工况下测得的位移信号的提纯过程。图5(a)、(b)为转子的原始振动信号，由图可知，信号受到了严重的噪声干扰。经SVD处理之后得到的奇异值曲线及其差分谱如图5(c)、(d)所示，由图可知，振动信号的奇异值差分谱的最大值都出现在序号4的位置。根据差分谱理论，选择前4个奇异分量进行信号重构，结果如图5(e)、(f)所示，据图可知，经SVD处理后的信号波形十分清晰，干扰成分几乎完全被消除。

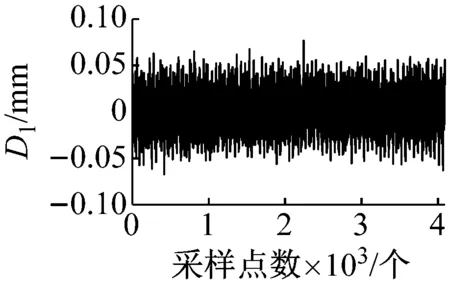
(a)D1的波形图

由图5中的提纯信号合成的轴心轨迹如图6所示。由图6可知，轴心轨迹为“花瓣形”，说明转子存在碰磨故障。

图6 提纯轴心轨迹

3.2 样本集划分

更换不同参数的试验轴承，采集不同转速工况下的振动信号，获得大量的试验数据。按照3.1节的方法获得椭圆形、香蕉型、外8字形和花瓣形4类不同轴心轨迹图各200张，按20%的比例随机选取测试集，其余为训练集。样本标签及数据集划分结果详见表2。部分提纯轴心轨迹，如图所示7所示。

3.3 模型设计

DCNN-FDM模型是基于tensorflow-gpu深度学习框架所搭建的，编程环境采用pycharm+python,处理器为intel(R)core(TM)i7-7700，显卡采用NVIDIA Geforce GTX 1050。该模型的设计包括训练和预测两个部分。模型训练时所用的网络结构如图1所示，其中输入层神经元个数等于输入轴心轨迹的样本个数，而输出层神经元个数与轴心轨迹的类别数一致。

(a)椭圆

在模型开始训练之前需要提前设置好超参数，本模型的基本参数设置如下：初始学习率lr设为0.001，以0.99的衰减率按指数衰减；训练周期150，采用小批量训练法，每次从训练集中随机输入16个样本；采用截断的标准正态分布函数进行初始化卷积层的权值参数，标准差设为0.1；卷积层后使用ReLu激活函数进行非线性映射；全连接层采用dropout技术来防止过拟。模型参数设置完成后，开始正式对网络进行训练。当模型训练次数达到预设值后保存模型参数并结束训练。然后进入测试阶段：将训练集输入到已训练好的模型当中，对比预测结果与真实标签，从而得到模型的准确率用于评价模型的性能。

3.4 轴心轨迹识别

采用训练集样本对DCNN-FDM模型进行训练，结果如图8所示。

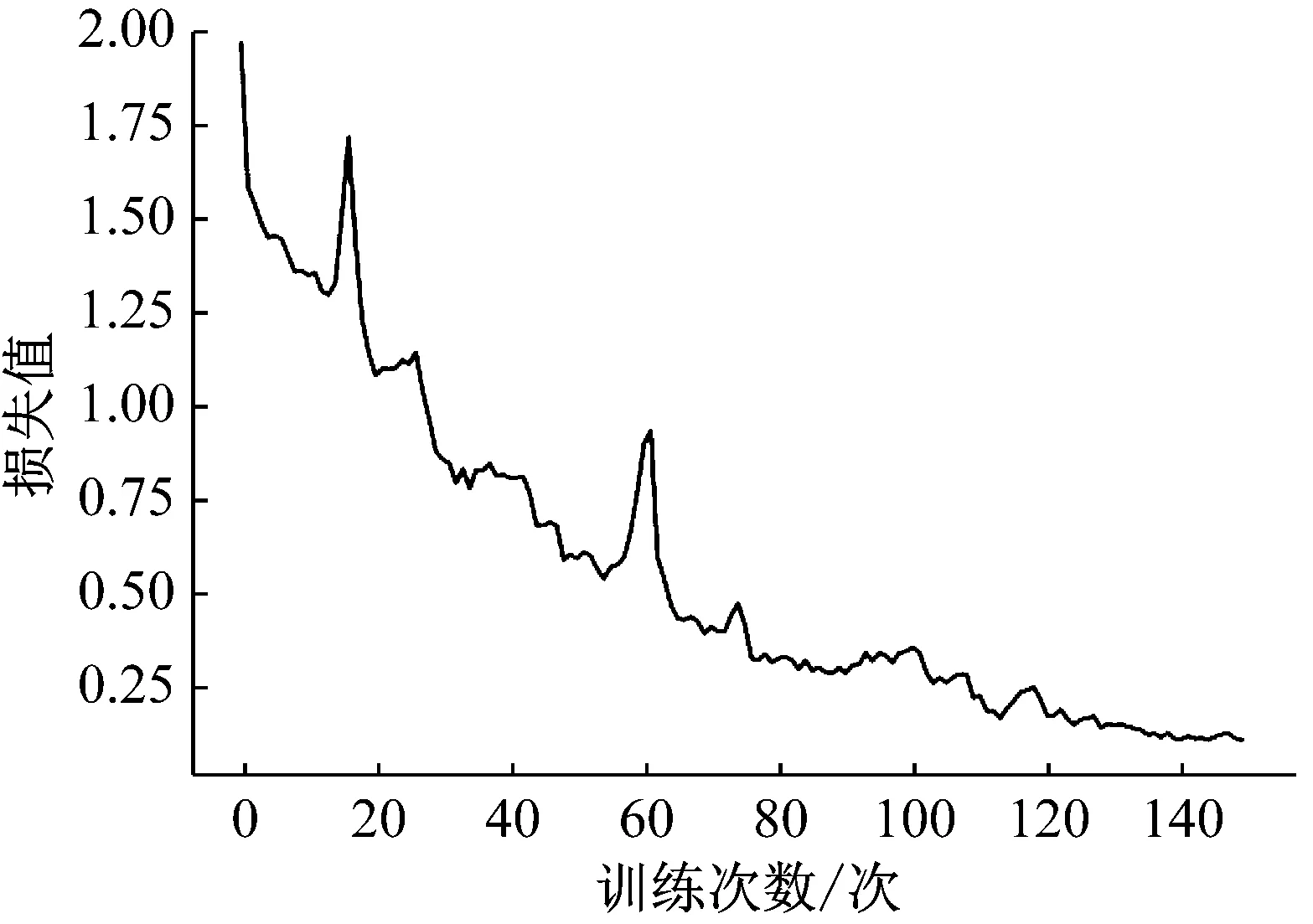
(a)损失值变化曲线

图8(a)为损失值变化曲线，由图可知，随着训练次数的增加，损失值不断降低，最终稳定在0.12左右。图8(b)为准确率变化曲线，由图可知，随着训练次数的增加，准确率不断交替上升且其波动幅度较大；当训练次数达到120次以后，准确率保持100%不变。然后，利用训练好的 DCNN-FDM模型对测试集进行预测。经过10次反复试验的结果如图9所示，由图9可知，轴心轨迹的识别率在96%～99%之间波动，平均识别率为97.09%。实验结果表明，DCNN-FDM模型对实测轴心轨迹的识别取得了良好的效果。

图9 DCNN-FDM模型的训练过程

经过分析发现，在4类轴心轨迹中，标签为“1”即香蕉形的轴心轨迹最容易被识别错误，其结果如图10所示。由图10可知，平均每次会有两张香蕉形轴心轨迹被识别错误，其原因将在后续小节给出。

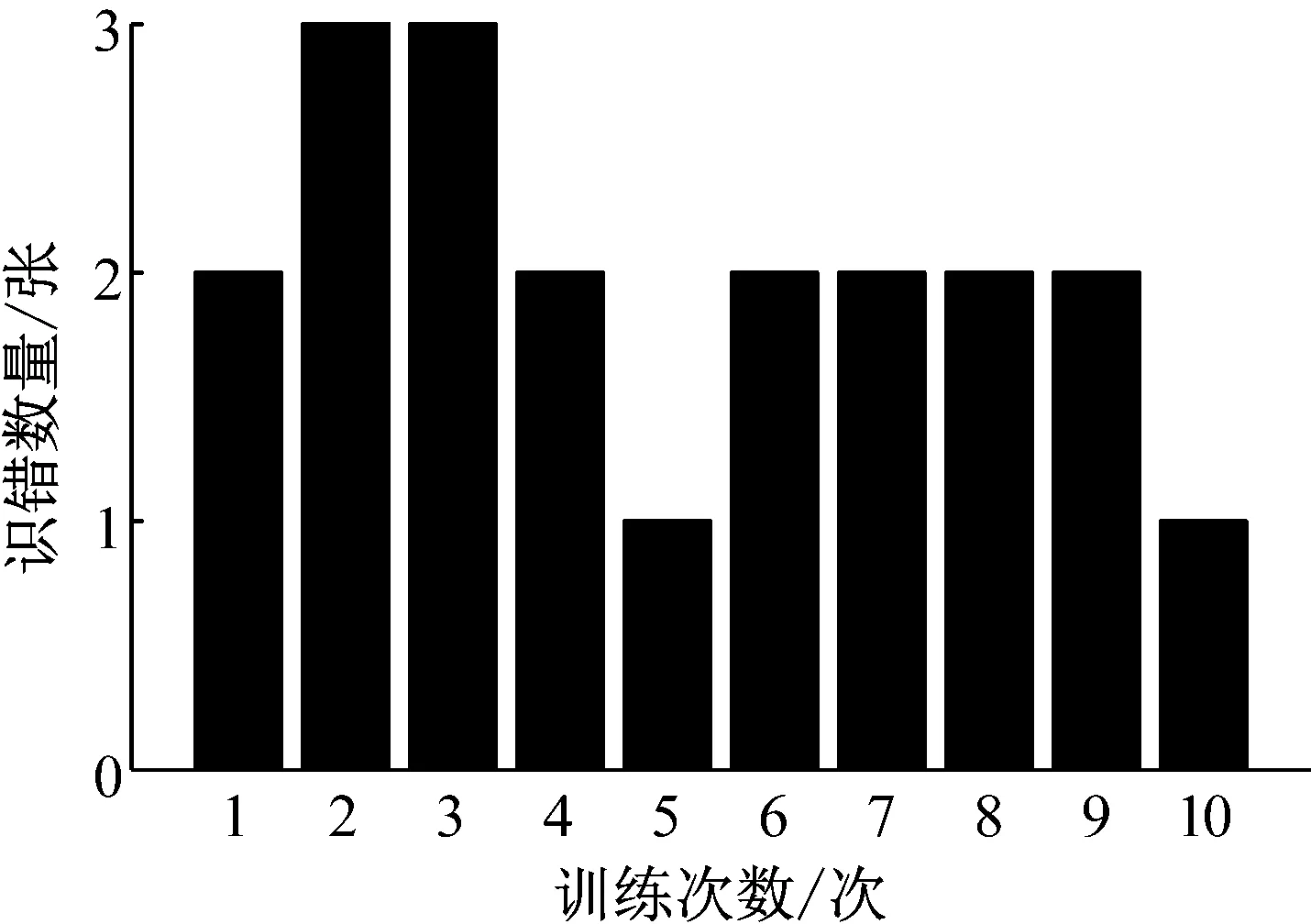
图10 椭圆形轴心轨迹识错情况

3.5 特征学习验证

为了验证所提模型对于实测轴心轨迹的自适应特征提取能力，在全连接层利用主成分分析提取这些特征中的前两个主成分，结果如图11所示，图中数字代表对应的样本标签，其具体含义见表1。图11(a)为第一轮训练的结果，由图可知，各类样本的特征混合在一起，由此推断模型的原始输入分类效果极差。图11(b)为第50轮训练的结果，由图可知，经过50次训练之后“不平衡”和“碰磨”故障已经明显可分，而“弱不对中”和“强不对中”故障仍然有部分特征混在一起。图11(c)、(d)分别为经过100次和150次训练的结果，此时各类特征已经明显分开，仅有少数几个“香蕉形”轴心轨迹对应的“弱不对中”故障特征落在了“外8形”轴心轨迹对应的“强不对中”故障特征区域内，这正是香蕉形轨迹最容易被误判的原因。由此可见，DCNN-FDM模型能够从实际数据集中学习到有效的特征并能实现转子故障的精确诊断。

(a)第1轮训练

3.6 模型对比

为了说明本文方法的优势，分别使用不同的传统方法(BP神经网络、hu矩+BP神经网络以及Hu矩+SVM)对相同的数据集进行测试，实验结果如表2及图12所示。结果表明，本文方法在各次实验中的准确率均比其他三种模型的要高，且其平均准确率为97.09%也是最高的；而Hu+BP及Hu+SVM的准确率较为接近，平均准确率分别为93.75%和94.23%；BP神经网络的识别效果最差，其准确率在75%～91%之间波动，平均准确率也仅为81.40%。产生上述结果的原因是：本文提出的DCNN-FDM模型是一种深度学习模型，具有强大的非线性拟合及特征学习能力；而其他三者皆为浅层的学习模型，学习能力有限，故诊断效果相对较差。

表2 不同模型对比结果

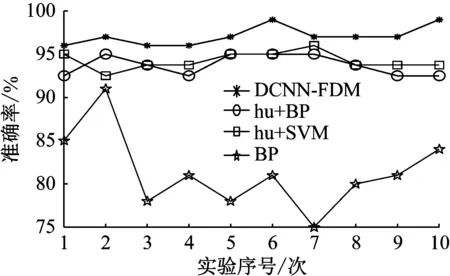
图12 不同模型诊断结果

4 结 论

本文基于深度学习的强大学习能力，借鉴卷积神经网络在门牌识别、手写字体识别等领域的成功应用，结合旋转机械不同形状轴心轨迹的特征，提出了将深度卷积神经网络用于在旋转机械的轴心轨迹识别，并通过对全连接层的前两个主成分进行可视化分析，以验证模型的自适应特征提取能力。试验结果表明，本文所用的DCNN-FDM模型较BP神经网络、hu矩+BP神经网络以及Hu矩+SVM的传统方法的识别效果好，前者可实现转子故障的精确诊断，识别率达到97.09%。DCNN-FDM模型的全连接层的主成分分析结果表明，所提模型确实具备自适应特征学习能力。