一道极坐标与参数方程高考题的教学设计*

广东省韶关市仁化县仁化中学(512300) 尹杰杰 刘雨昀

1 引言

极坐标与参数方程在历年全国卷中是选做题, 分值10分,属于中档题.设置两小问,第一问5 分,一般为极直互化或参数方程与普通方程互化,属于简单题.第二问5 分,一般考查以下几种类型: 第一,极径ρ的几何意义与应用.例如:2015年全国I卷、2015年全国Ⅱ卷、2016年全国Ⅱ卷、2017年全国Ⅲ卷;第二,参数的几何意义与应用.例如: 2018年全国Ⅱ卷、2018年全国Ⅲ卷;第三,直线与曲线的位置关系,利用点参法求最值.例如2016年全国Ⅲ卷、2017年全国I卷、2019年全国I卷;第四,利用极坐标或者参数方程求曲线的轨迹方程.例如2017年全国Ⅱ卷、2019年全国Ⅱ卷; 第五,利用分类讨论思想求解.例如: 2018年全国I卷、2019年全国Ⅲ卷.

下面笔者通过对2019年数学全国I卷第22 题“极坐标与参数方程”进行例题教学设计及例题改编与变式.

2 例题教学设计

例题(2019 全国I卷)在直角坐标系xOy中,曲线C的参数方程为(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为

(1)求C和l的直角坐标方程;

(2)求C上的点到l距离的最小值.

师: 这是一个什么问题? 第一问主要考查什么知识点?解题的基本程序是什么?

(极参问题是学生掌握较好的题型,原因是模型单一,学生熟悉,旨在引导学生将解题思路调控进入自己熟悉的区域,也想进一步巩固极坐标、参数方程、直角坐标方程的转化的解题程序.)

生1: 这是一道极坐标与参数方程的题目,第一问主要是考查坐标系转化和消参.首先通过x的等式,求出x的范围,然后通过代入消元法消去参数t,化简得到了缺了一个点的椭圆方程,然后利用公式对直线l的极坐标方程,转化为直角坐标方程即可.

生1 解法: (代入消元法)

对于曲线C, 由题意知−1＜x≤1,所以因为所以得到把代入到有化简得易知l的直角坐标方程为

师: 对于曲线C,除了代入消元法,还有其他方法吗? 曲线C的结构有什么特征? (旨在引导学生观察式子特征,并联想到平方公式.)

生2: 可以通过观察法,看出x,y式子的特征,发现分母都是1+t2,而分子是1−t2,4t,一个二次,一个一次,我们有等式(1+t2)2−(1−t2)2=4t2,故而可以想到通过平方的形式构造出与分母相关的完全平方式即可.

生2 解法: (平方消参法)

师: 此法是通过观察式子特征,构造平方,从而大大减少了计算量,但是此法对学生核心素养要求较高,大多数学生无法想到.那我们是否还有它法求解呢? (学生激烈讨论中)

师: 通过生2 的观察法,是否发现曲线C的参数方程和某一类公式很像? (小部分同学说出答案)

师: 再看看x的取值范围,和哪个函数的取值范围很像?

生3: 三角函数,曲线C的参数方程结构很像万能公式.

师: 很好,是通过万能公式进行代换,请写出你们的解答过程,生3 板演过程.

生3 解法: (万能公式法)

因为−1＜x≤1,令代入可得化简得所以

评析本问题的三种解法各有特色.代入消元法,思路清晰,容易落笔,但过程繁杂,计算量大;平方消参法,过程简短,计算量小,但素养要求过高,学生思维定势,不易想到;万能公式法,是此类题型的通法,但教学过程中,由于大纲要求不高,故而对此法讲解较少,学生掌握不熟练,易出现计算失误.

师: 下面进行第二问,主要考查什么知识点,我们应该从哪里入手?

生4: 主要考查直线与曲线的位置关系,求曲线上的点到直线的距离最小值,利用点参法与点到直线的距离公式,然后通过辅助角公式,转化正弦型函数求最值即可.

生4 解法: (点参法)

直线l的极坐标方程转化为直角坐标方程为2ρcosθ+

得:

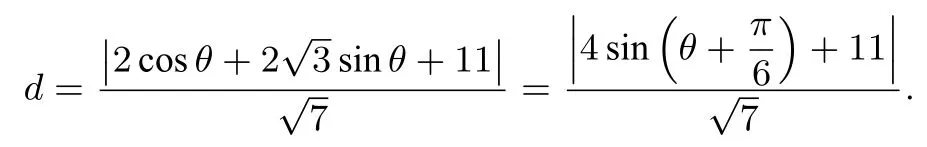
因为−π ＜θ ＜π,所以所以当且仅当,此时θ=有

师: 生4 主要通过点到直线的距离公式,进行求解.是否还有其他解法?

生5: 可通过设出与直线l平行且与曲线C相切的直线l1,然后联立曲线C与l1,利用判别式求解即可.

生5 解法: (判别式法)

设与直线l平行的直线方程为故由题可知,当且仅当直线l1与曲线相切时,切点到直线的距离是最大或者最小值.联立方程化简可得4×4×(m2−4)= 0,得m=±4.显然可知,当m=−4时, 直线l1与曲线相切的切点到直线l的距离最大, 故所以当m=4 时,直线l1与曲线相切的切点到直线l的距离最小,故

师: 本问是否还有其他解法呢?

师: 当我们对曲线的参数方程无从下手时,我们可以如何求解曲线上的点到直线的最小值呢? 我们是否可以不用化简的参数方程求解呢?

生6: 硬解.

师: 是的,很好! 本问题还有一个暴力解法,就是直接将曲线C上的点设为然后通过点到直线的距离公式,变为一个关于参数t的式子,然后转化为二次一次方程,利用判别式求出参数t的范围,进而求出最小值.

生6 解法: (暴力硬解法)

设曲线C上的点M的坐标为则点M到直线的距离为

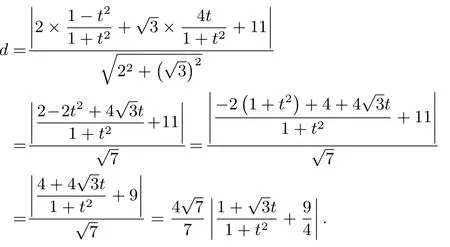
师: 通过以上解法,我们可以发现,本题主要体现了哪几个数学核心素养? (同时引导学生总结以上方法.)

生: (齐答)数学运算和直观想象.

评析本问一个是几何法,两个是代数法.几何法过程简洁,代数法,通法运算量大,但思路清晰,尤其在学习了解析几何后,部分学生更热衷于通过联立方程求解.

本题主要考查学生对极坐标、参数方程与直角坐标方程的转化,和利用椭圆的参数方程解决“距离”问题,难点在于参数方程的消参,对于分式消参,大多数学生方法掌握不熟练和运算能力不强, 以致于对难度较小的第二问没有作答,从而导致失分严重.

高考试题一般是来源于教材,又高于教材.大多是依据课本例题、课后习题、探究问题等进行加工重组改编,由浅入深,循序渐进.本题中曲线C的参数方程就是人教B 版选修4-4 第二章第二节的课本里练习原题,这也透露出我们在备考过程中,不能忽视教材中的重点例题、练习、探究问题的复习回顾.

为了让学生更好的掌握本题知识点,下面笔者对本题进行了适当改编.

改编1在其他条件不变的前提下,把第二问改为求直线上的点的坐标到曲线C 的最小值.

设计意图: 原题求点距值最小值,改编之后,求取到点距最小值时点的坐标,这样主要是让学生更直观清楚的知道点的具体位置,能更好的理解本题考查知识点,检验学生对例题的掌握程度.

解: (点参法)

直线l的极坐标方程为化为直角坐标方程为将曲线C化成参数方程形式为:(θ为参数,−π ＜θ ＜π),则曲线C上的点可以设为M(cosθ,2 sinθ),所以由点到直线的距离公式可得:

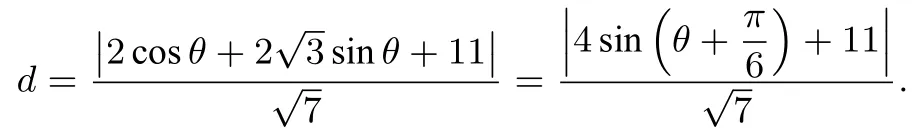
因为−π ＜θ ＜π,所以所以当且仅当此时有

改编2在其他条件不变的前提下,直线l的极坐标方程改为且C上的点到l的距离的最小值为求a.

设计意图: 本题的改编与2017年全国理科I卷第22 题极为相似,通过逆向思维设问,引入参数a,考查分类讨论思想与数形结合思想,可以很好的提升学生数学核心素养.

解: (点参法)

直线l的极坐标方程为化为直角坐标方程为将曲线C化成参数方程形式为:(θ为参数,−π ＜θ ＜π),则曲线C上的点可以设为M(cosθ,2 sinθ),所以由点到直线的距离公式可得:所以故当a≥0 时,有|−4+a|=7有, 解得a= 11, 或a=−3(舍去) .当a ＜0 时, 有|4+a|= 7 有, 解得a=−11, 或a= 3(舍去) .综上可知,当a=11,或a=−11 时,C上的点到l距离的最小值为

下面再看三个与2019年全国1 卷相似度极高的变式练习.

变式1(2017 江苏)在平面坐标系xOy中,已知直线l的参考方程为(t为参数),曲线C的参数方程为(s为参数).设P为曲线C上的动点,求点P到直线l的距离的最小值.

变式2(2017 全国I卷)在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t为参数).

(1)若a=−1,求C与l的交点坐标;

(2)若C上的点到l距离的最大值为√求a.

变式3(2016年全国III卷)在直角坐标系xOy中,曲线C1的参数方程为(α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为

(I)写出C1的普通方程和C2的直角坐标方程;

(Ⅱ)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.

评析通过历年高考题,我们不难发现在高考题中极参题目考查的知识点与题型相识度极高,由于篇幅有限仅列出以上三道高考真题,所以研究历年高考题是我们一线教师把握高考动态方向最有效的方法.改编l 主要是让学生更直观清楚的知道点的具体位置, 能更好的理解本题考查知识点,检验学生对例题的掌握程度.改编2 引入参数a,其目的是使学生掌握分类讨论思想,引导学生巧用椭圆的参数方程解决“距离问题”.增强数学能力和探究意识.提高学生数学核心素养.两个改编,三个变式层层深入,这无疑是本节课的一个亮点,给学生提供了良好的探究情境,促进学生主动学习.通过以上改编和变式,我们可以启发学生理解数学本质,掌握数学思想.因为在学生的“最近发展区”设计恰当的具有针对性、符合本节课程要求的改编题目,并给给学生提供了探究和交流的机会,让学生在自主探究、合作交流的过程中提升数学核心素养.

3 总结与反思

本节课例题第一问主要是极参与直角系转化问题,第二问主要是直线与椭圆的位置关系问题求距离.一方面考查了学生对极坐标与参数方程的基础知识掌握程度,另一方面考查了学生数学运算与逻辑推理素养,培养了学生数学问题的探究意识.例题的难点主要体现在消参与参数范围的确定.所以本例题的教学设计思路也是根据学生的最近发展区,引导学生思考,循序渐进、层层深入,强化学生的基础知识和基本技能,培养学生系统归纳知识的能力,增强探究问题的意识,符合学生的思维发生发展过程.

在教学过程中,与学生交流互动,为学生创设轻松的学习环境,通过设问的形式,对数学的思想方法进行了适当的引导,使得学生在解题的过程中,能发散思维,一题多解,帮助学生理解知识的横向联系、纵向发散.通过在多解中求简、在修正中优化,能够让学生体验解决问题的思维过程,将能力的提高落到实处,可以很好地提升学生的数学核心素养.

本节课在引导学生思考时,既从代数法,又从几何法两个方面着手,学生有章可循,这样能够激发学生的学习热情,拓展学生的思维,提高教学效率.同样,本节课也存在以下几点需要改进的地方: 第一,课堂容量较大,难以关注到全体学生的习得情况;第二,引导较多,可采用互助学习小组合作讨论的方式进行部分数学活动等.纵观整堂课,虽然存在个别不足之处,但是整体来说,亮点较多,同时能很好的培养学生的数学核心素养,所以仍是一堂非常成功的课.