基于数字图像相关法的针织物泊松比测定

杨 可，王朝晖

(1.东华大学 服装与艺术设计学院，上海 200051； 2.东华大学 现代服装设计与技术教育部重点实验室，上海 200051)

泊松效应是材料在垂直于载荷方向收缩(膨胀)的现象，泊松比是泊松效应的一种度量，为垂直方向上与载荷方向上应变之比[1]。泊松比表征材料的基本力学属性，影响材料的力学性能。在纺织材料中，泊松比是计算机模拟服装压力分布和面料悬垂性等力学性能以及图案设计的重要参数。针织物相比机织物存在明显的泊松效应，针织服装容易在一个方向发生拉伸时，另一个方向也发生较大的变形，很大程度上影响了服装穿着时的外观效果[2]，因此，泊松比是针织物不可忽略的重要参数[1]。由于针织物是非连续介质且各向异性，不满足由弹性模量与切变模量推导得出泊松比的条件，也不适用于连续介质的泊松比测量方法，并且对针织物进行单轴向拉伸时，在载荷方向上针织物会出现颈缩现象，导致试样在拉伸过程中不同位置的泊松比不同，存在泊松比的实际值与不同位置泊松比的计算值不一致的问题[3]。因此，准确可靠地测定针织物泊松比还存在一定难度。

张莉等[4]通过测定经纬向以及45°方向的拉伸模量，使用简单网格模型间接计算泊松比，但该方法误差较大且仅对平纹织物有较好的适用性。有的利用KES-G2双向拉伸仪对机织物和针织物进行测试，把弹性力学平面应力问题的理论用于描述织物的双向拉伸，提出双轴拉伸法计算泊松比的方法[2]。Zhou等[5]基于正交各向异性理论和条带双轴拉伸实验，提出了弹性针织物泊松比的测试方法。虽然双轴向拉伸可以在一定程度解决织物拉伸时颈缩不一致现象，相比间接测试降低了误差，但是以织物泊松比的定义来确定双轴向拉伸测试方法比较复杂，还需测定织物的弹性模量进行换算。

近几年光学图像法因具有不需与样本接触便可进行局部测量、捕捉非均匀变形以及不需要借助于数值或分析模型的直接测量的能力[6]而在泊松比测试中得到了广泛应用。高晓平等[7]应用CCD摄像机拍摄土工布试样拉伸变形前后的图像，在Photoshop软件中调入试样拉伸前后的图像，提取图像中的尺寸，从而计算出泊松比。有的研究利用KES-FB1对试样进行拉伸变形测试，并用视频记录测试过程，测定了最大拉伸变形1%时的泊松比[3]。图像分析使用After Effects软件裁剪图像序列，利用Adobe Illustrator的标尺功能，测量试样的横向和纵向尺寸变化，仅选择了试样的中心点作为测量部位，尺寸测量时间间隔为1 s。韩晓果等[8]通过在双向紧密织物样品织物中心位置设置9个等距点，构成4个正方形，利用单向拉伸过程中测得的织物中这些离散点之间的距离变化，从而得出泊松比的实时动态变化情况，但也仅选择了9个点进行测量，以5%应变间隔作为动态变化并没有真正达到实时测定。上述测试方法都用视频录制了拉伸过程，导出图片后再用Photoshop或AI图像处理软件中的标尺功能对局部点的位移进行测量，测量容易受主观因素干扰，并且所选取测量的2张图片的间隔较长，因此精度较低且不能整体反映织物的泊松比。

数字图像相关技术作为一种光学非接触测量解决方案，相比普通图像处理软件有着较高的精度，已应用于混凝土、岩石、橡胶等材料泊松比的测定[9-11]。Hursa等[12]用数字图像相关法也成功地测定了纺织试样的泊松比，在拉伸实验机上对织物试样进行1%应变拉伸载荷实验，同时用数码摄像机录制拉伸过程，提出了用数字图像相关法确定机织物泊松比的方法，该方法仅在小应变拉伸载荷下测量了织物泊松比。

虽然学者们对织物泊松比测定方法进行了不同的探索，但是对于织物颈缩问题，以及在较大应变下的精度问题仍然有待提高。本文结合数字图像相关法对针织物进行单轴拉伸测试，提出了一种以试样整体作为研究对象的针织物在较大形变下的泊松比测试方法，本文研究可为针织物泊松比的测定提供参考思路。

1 数字图像相关法

1.1 数字图像相关法原理

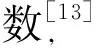
(1)

i*=i+a

(2)

j*=j+b

(3)

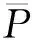
1.2 计算应变

在应用数字图像相关法时，计算机将比织物按网格划分为若干个像素点，假设将织物被网格纵向分成n份，每份横向分成m个点，织物拉伸前的长度为l，拉伸后的长度为l′，则每份的长度为0,l/n,…，nl/n，伸长后每份的长度为0,l′/n, …，nl′/n,则所有点的平均应变ε测见式(4)。

(4)

因此本文实验泊松比的计算是在整个试样中的有效范围内进行取点，所有点的平均位移代表整块试样的应变值，可以避免因织物沿拉伸方向上两夹头间出现不同程度的颈缩现象而难以确定试样的取点位置，进而导致织物不同位置所测得的泊松比值不同的问题。

2 实验设计

2.1 织物选择和假设

本文选择3种织物，每种织物试样准备3块，织物规格参数见表1。可知，3种织物中均含有一定量的氨纶成分以保证面料具有较低的弹性模量，防止在拉伸过程试样断裂。

表1 织物规格参数

试样的载荷方向为织物纵向，实际尺寸为20 cm×5 cm，在仪器中的有效尺寸为10 cm×5 cm，为避免测量过程中试样边缘卷边的影响，实验测量尺寸为10 cm×4 cm，在保证不改变试样力学性能情况下，在试样上随机点上红蓝绿色墨水以便形成计算机可识别的纹理，试样示意图见图1。

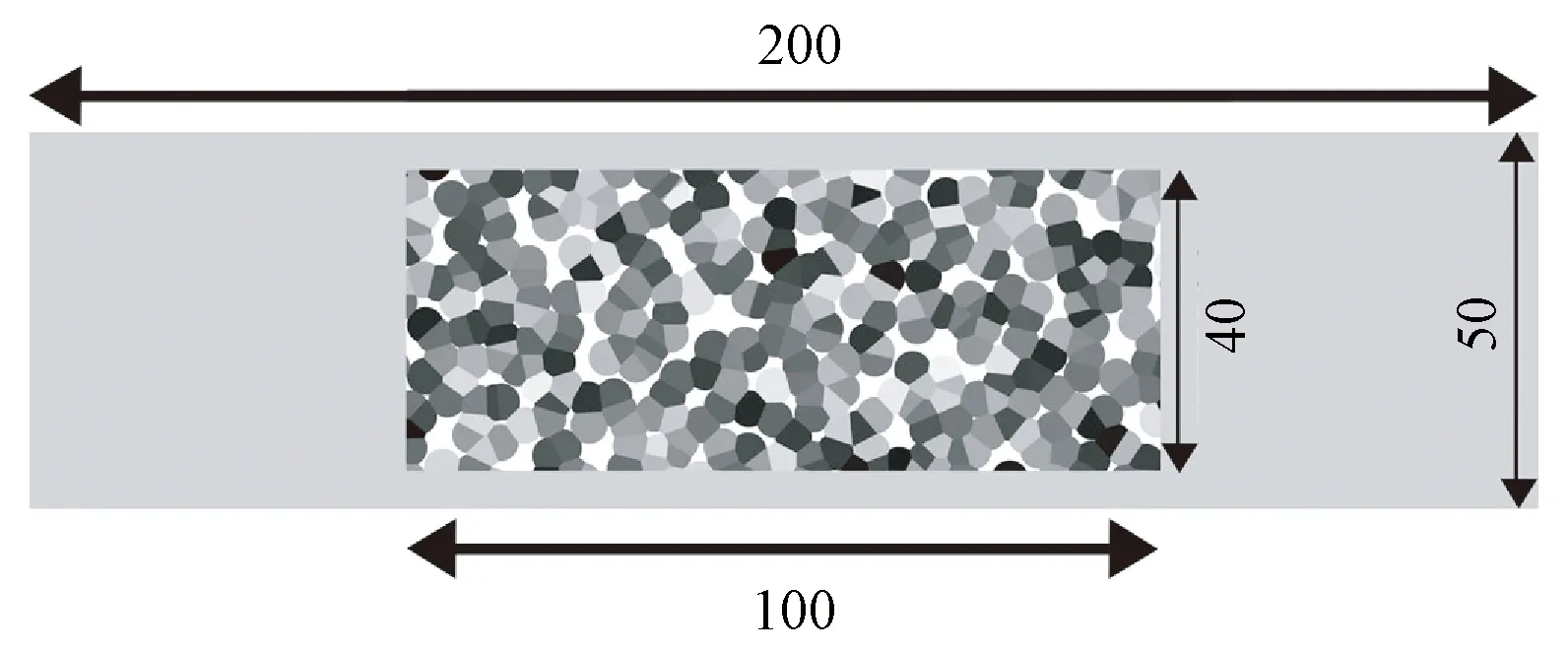
单位：mm。图1 试样示意图

为了统一管理实验和分析，本文做2个主要假设:①由于试样厚度较小，在拉伸过程中，忽略沿厚度方向的应力分量。因此，本文仅讨论针织物的二维平面泊松比。②人体穿着服装时，一般弹性服装面料拉伸率低于30%，结合针织物的力学性能，本文试样的拉伸率设计为15%。

2.2 实验部分

泊松比测试流程见图2。首先用摄像机记录试样在Instron万能测试仪中拉伸的整个过程，其中Instron万能测试仪记录了试样载荷方向的拉伸长度随时间变化的实际值，然后将录制完成的视频导出每1帧图像，灰度化处理后用数字图像相关法得到载荷方向的位移以及垂直于载荷方向的位移随时间变化值，并将载荷方向的实际值与计算值做比较。

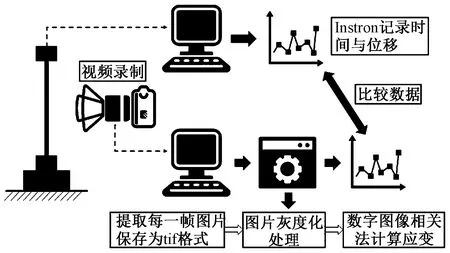
图2 泊松比测试流程

2.2.1 拉伸实验

实验在标准状态下进行，温度(20±2) ℃，相对湿度(65±2)%，实验前试样已进行24 h的调温调湿。利用Instron万能测试仪进行实验，沿试样长度方向进行拉伸，拉伸速度为100 mm/min，直至应变为15%。

2.2.2 图像采集

用摄像机记录试样拉伸过程，摄像机采用1 200万像素广角摄像头Sony IMX386和1 200万像素长焦摄像头Samsung s5k3m3，其中长焦镜头为56 mm焦距；广角镜头为27 mm焦距，所录制的视频分辨率为1080p，帧率为30帧/s，在Adobe Premiere Pro CC 2019中将每1帧图片导出为tif格式，在Adobe Photoshop CC 2019中进行批量灰度化处理。

2.2.3 数字图像相关法实验

用MatLab软件编写程序进行位移和应变计算，数字图像相关法分析流程见图3。该程序由约翰霍普金斯大学的Christoph Eberl[14]团队开发。

图3 数字图像相关法分析流程

本文实验使用MatLab R2018a (9.4.0.813654) 进行实验。分析图像的步骤如下：

①执行filelist_generator.m文件，自动创建包含每1帧灰度图像文件名的列表，将其保存为文件filenamelist.mat，并创建time_image列表，用于合并每1帧的应变。

②执行grid_ generato.m文件，在第1帧图像上创建标记，本文采用矩形网格进行标记，每1帧图像网格水平和垂直方向设定为30像素，通过标记跟踪位移，网格数据保存为文件grid_x.dat和grid_y.dat。

③不同拉伸率时试样的分析图像见图4。执行automate_image.m文件，打开filenamelist.mat文件中的第1帧图像，此图像将显示在图形窗口中，标记位置为图4中颜色较浅处，计算第1帧图像和第2帧图像之间的相关性，相关系数计算根据式(1)，然后显示第2帧图像，标记位置为图4中颜色较深处，继续计算第2帧图像和第3帧图像之间的相关性，重复上述过程，直到文件filenamelist.mat中的最后1帧图像。

图4 不同拉伸率时试样的分析图像

④执行displacement.m文件，进行位移分析，通过对每1帧图像中所有位移的位置进行分析计算出x、y轴方向的应变，并在最后1帧图片上删除一些拟合欠缺的标记，最终得到有效网格点的平均应变。

3 实验结果及分析

3.1 计算应变与实际应变检验

为了检验采用数字图像相关方法的准确性，将试样载荷方向应变的计算值与实际值做比较。以0.5 s为间隔提取数据，试样载荷方向应变计算值与实际值见表2。

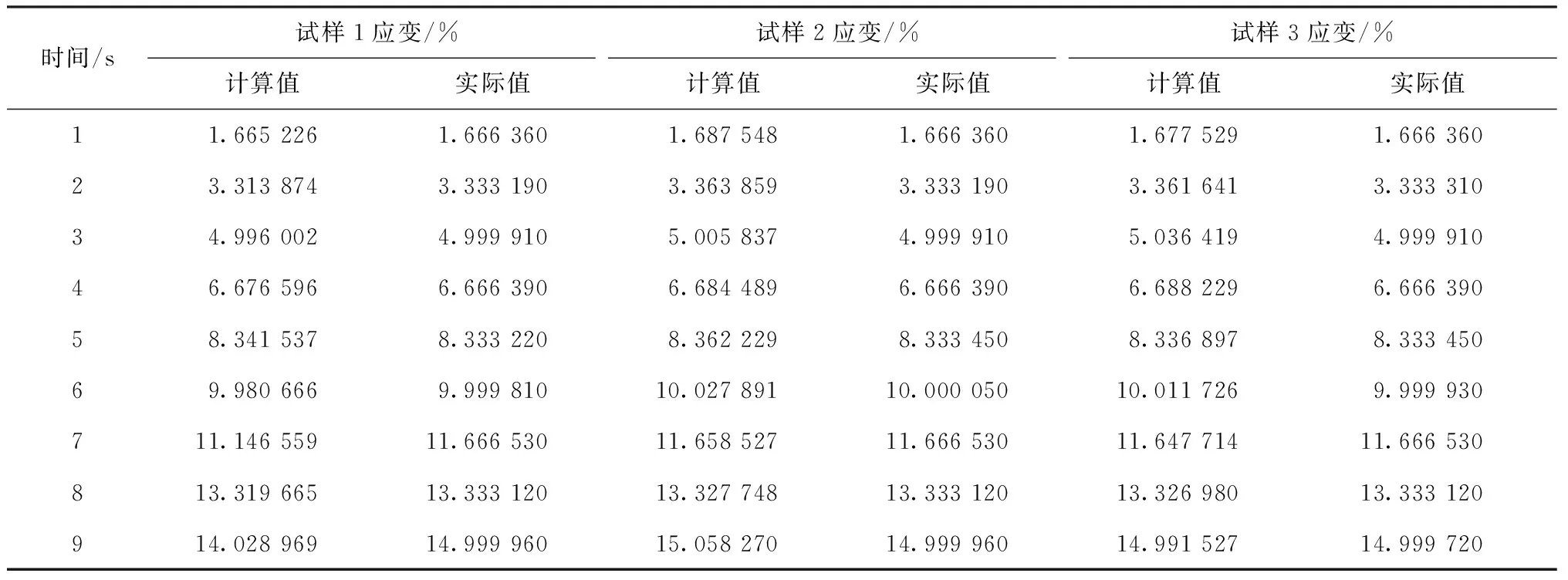
表2 试样载荷方向应变部分计算值与实际值

用IBM SPSS Statistics24对3种试样的实际应变值与计算应变值做独立样本t检验分析，在95%置信区间里，独立样本t检验结果和相对误差见表3。3组试样的显著性sig值均大于0.05，表明实际应变值与计算应变值无显著差异，数字图像相关法得到的结果与实际结果具有高度的一致性。通过数字图像相关法得到的试样载荷方向的应变与实测应变的相对误差范围为0.05%～4.90%，误差可能由机器启动时的小幅度抖动造成。

3.2 泊松比计算

泊松比ν的计算公式[4]见式(5)。

(5)

式中：Ax与By分别为垂直载荷方向和载荷方向；εAx为垂直载荷方向的应变；εBy为载荷方向上的应变。

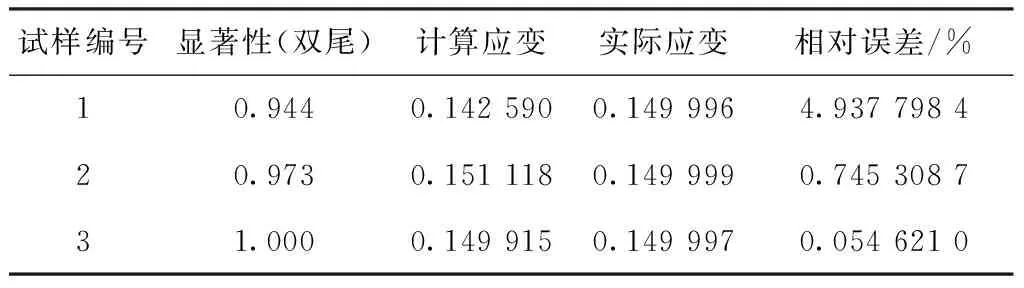
表3 独立样本t检验结果和相对误差

由数字图像相关法得到的每1帧图像载荷方向的应变与垂直于载荷方向的应变，每1帧状态时织物的应变见图5。

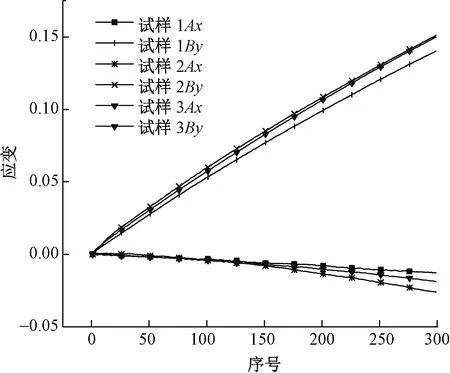
图5 每1帧状态时织物的应变

根据式(5)求得试样的泊松比，3种织物在每1帧状态时织物的泊松比见图6，即随着载荷方向拉伸率不断增加泊松比的变化。

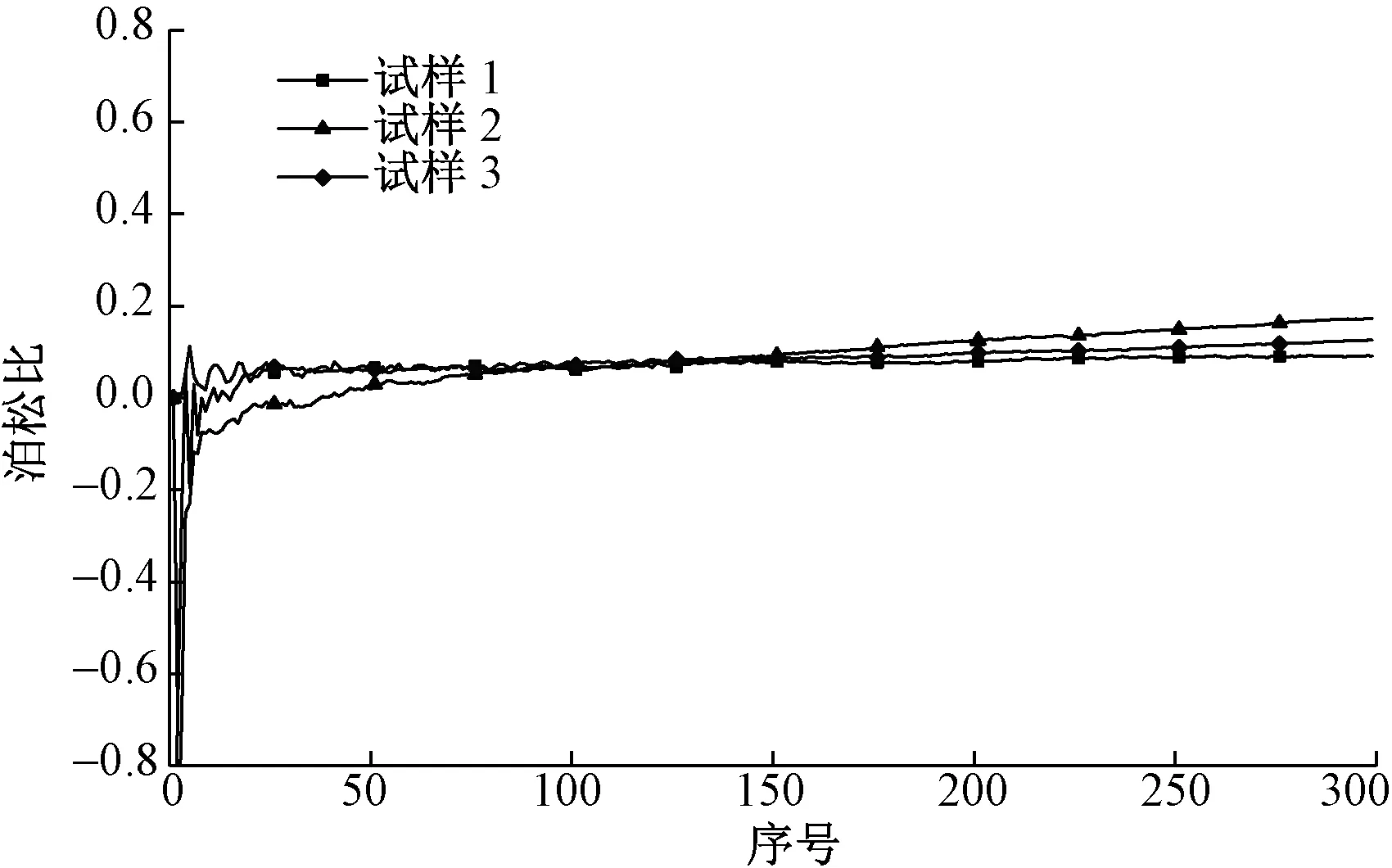
图6 每1帧状态时织物的泊松比

由于仪器在启动时存在一些晃动，在前30帧图像中，即仪器启动第1 s内试样的泊松比存在较大波动。3种织物在拉伸率为1%、5%、10%、15%时的织物泊松比见表4。可见，当试样拉伸到15%的过程中，计算所得泊松比的数值都处于正常参考范围内(0～0.5)，符合泊松比数值。对于同一块织物，其泊松比的变化趋势相似，随着织物沿载荷方向拉伸逐渐加大，泊松比整体呈上升趋势。对于不同织物，试样2、3的泊松比分别大于试样1的泊松比，由于试样2、3的横纵向密度小，与试样1相比存在较大空隙，而空气的泊松比为零，因此相对于密度小的织物垂直于载荷方向的应变较大，而载荷方向的应变相同，因此密度小的织物泊松比较大。

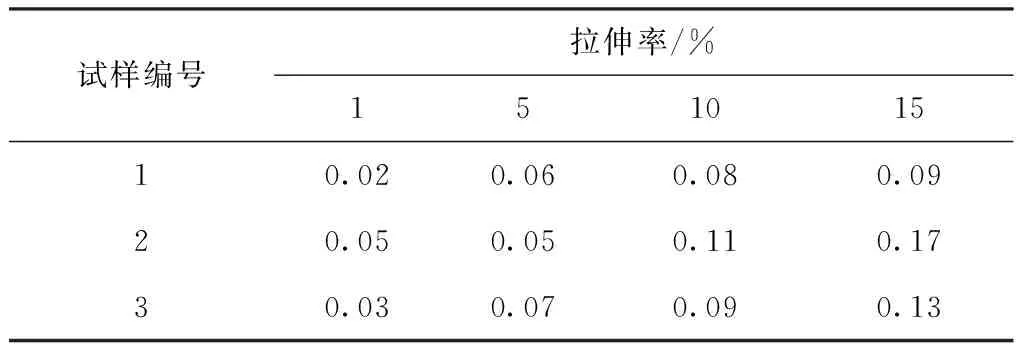
表4 织物泊松比

4 结 论

针织物在拉伸变形下具有显著的泊松效应，但是快速且准确地测量织物泊松比目前还存在一定难度，本文提出的数字图像相关法测定针织物泊松比，使用Instron万能测试仪对3种不同的织物进行单轴拉伸实验，录制视频并提取每1帧图像，在灰度化后进行相关性位移分析，并对试样载荷方向的计算应变与实际应变做t检验分析，显著性大于0.05，表明具有高度的一致性，最后计算所得泊松比处于正常范围，相对误差在5%以内。本文提出的泊松比测定方法避免了织物颈缩问题，且每秒可提取30帧图片进行位移分析，提高了精度，因此应用数字图像相关法测定针织物的方法是可行的，适用于任何针织物，有较佳的应用价值，为研究针织物的泊松比提供了新途径。