人教版四年级数学河内塔游戏推广的教学研究

广东省广州市花都区花东镇李溪小学 张升添

新人教版四年级数学上册第111 页游戏——河内塔游戏（又名汉诺塔游戏）：（如图1 所示）你能借助②号杆把①号杆上的珠子移到③号杆而不改变珠子的上下顺序吗？最少移动多少次？移动规则是：每次只能移动1 个珠子，且大珠子不能放在小珠子上面。如果①号杆上有4 颗珠子呢？

图1

这个游戏问题，①号杆上有3、4 颗珠子时，学生通过真实的游戏容易明白、理解。为了发展学生智力，提高学生的逻辑思维能力，把这个问题深化，在课堂数学教学中，把这个数学游戏问题推广到①号杆上有5、6、7、…、n颗珠子的情况。这样就将游戏变为数学问题，真正体现数学游戏问题，借此问题对学生渗透“由简单到复杂，由具体到抽象”的数学思想方法：

设①号杆上珠子颗数为n，为了下文表述方便，记游戏的最少移动次数为f（n）。四年级学生初涉的抽象知识不易理解，教师要多举例说明，本文着重研究这一游戏问题的规律的课堂数学教学方法，在课堂数学教学中，引导学生理解这个数学游戏问题的一般规律：f（n）=2×f（n-1）＋1。

首先，当①号杆上珠子颗数n=1、2 时，学生尝试操作。学生通过实际操作探索珠子移动的最少次数f（1）、f（2），容易理解f（1）=1、f（2）=3。

其次，当①号杆上珠子颗数n=3、4 时，学生探索珠子的移动最少次数f（3）、f（4）。一部分学生理解f（3）=7、f（4）=15，有一部分学生不能理解。这时教师要实际操作移动珠子，让学生明白怎样操作移动珠子，从而理解f（3）=7、f（4）=15。

（1）当n=3 时，一定要经过如图2 所示的移动操作，上一步的移动操作如图3 所示。

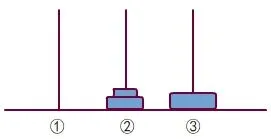
图2

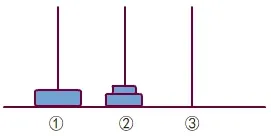
图3

而由图1 的①号杆上面的两个较小珠子经过f（2）步移动操作得到图3，再经过一步移动操作得到图2，再把图2 的②号杆的两个珠子经过f（2）步移动操作得到图4。

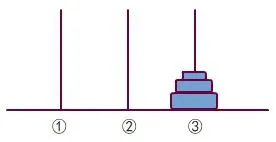
图4

由此得到当n=3 时，最少移动次数f（3）=f（2）＋1 ＋f（2） =2×f（2）＋1=2×3+1=7。

数学教学中，有些学生不明白图1 的①号杆上面的两个较小珠子经过f（2）步移动操作得到图3，教师要动画演示或实操演示：

图5

由此可见，由图1 经过f（2）=3 次移动操作得到图3，实际是把图1 的①号杆上面的两个较小珠子移动到②号杆，故移动操作次数为f（2）=3。移动过程如图5。

同理，由图2 经过f（2）=3 次移动操作得到图4，实际是把图2 的②号杆上的两个较小珠子移动到③号杆，故移动操作次数为f（2）=3。移动过程如图6。

图6

（2）当n=4 时，由图7 经过f（3）=7 次移动操作得到图8，实际是把图7 的①号杆上面的3 个较小珠子移动到②号杆，再把图8 的①号杆上的大珠子经过1 次移动操作移动到③号杆，得到图9，再由图9 经过f（3）=7 次移动操作得到图10，实际是把图9 的②号杆上的3 个珠子移动到③号杆。

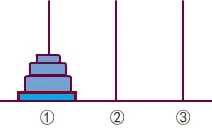
图7

图8

图9

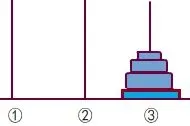
图10

由此得到当n=4 时，最少移动次数f（4）=f（3）＋1 ＋f（3） =2×f（3）＋1=2×7+1=15。

最后，一般地，①号杆上有n颗珠子，至少经过f（n－1）次操作移动，把①号杆上较小的（n－1）颗珠子移动到②号杆；再把①号杆上最大的珠子经过1 次操作移动到③号杆；再经过f（n－1）次操作移动，把②号杆上较小的（n－1）颗珠子移动到③号杆上。由此得到：f（n）=f（n－1）＋1 ＋f（n－1）=2×f（n－1）＋1。

这样，借此问题对学生渗透“由简单到复杂，由具体到抽象”的数学思想方法。