高压天然气非恒定速率泄漏扩散数值模拟研究*

程方明，张安邦，王 焘，罗振敏，王 涛，陈 言

(1.西安科技大学 安全科学与工程学院，陕西 西安 710054；2.西安市城市公共安全与消防救援重点实验室，陕西 西安 710054；3.兵器工业卫生研究所，陕西 西安 710065)

0 引言

在天然气工业中，压缩天然气(Compressed Natural Gas，CNG)生产、储存、运输、使用一般在高压容器中，且工艺涉及设备多，流程复杂。高压容器及附属设施在使用过程中常因腐蚀或操作失误导致天然气泄漏。天然气储配厂储存大量高压天然气，一旦发生泄漏，遇明火会发生火灾或爆炸，对人员安全、公共设施及周边环境造成严重威胁。因此研究储配厂高压天然气泄漏，加强此类事故的预防与控制很有必要。

国内外学者对气体泄漏与扩散做了大量研究：Li等[1]通过使用FLACS软件研究安全间距对气体扩散的影响发现，安全间距降低船型和圆柱形浮式液化天然气(FLNG)结构中的气云尺寸，增大圆柱形FLNG结构气云尺寸；董刚等[2]采用FLUNT模拟高压管道内天然气泄漏与扩散过程，研究风速对扩散过程的影响；Li等[3]使用CFX软件模拟LNG燃料船发动机室中天然气泄漏扩散，优化气体探测器布局；Birch等[4-5]首次定义虚拟喷口，通过质量和动量守恒定律，推导出虚拟喷口处各有效物性参数，进一步完善气体泄漏模型；Chenoweth等[6-7]基于理想气体模型，提出适用于Abel-Noble状态方程的泄漏模型；Chefer等[8]对理想气体模型和Abel-Noble状态方程的泄漏模型预测结果进行对比发现，2者差异较小；刘凯迪[9]通过建立2区模型对高压欠膨胀H2射流进行数值模拟研究；刘自亮等[10]修正Brich泄漏模型，并结合CFD软件模拟气体泄漏及扩散过程；李雪芳等[11]提出基于理想气体状态方程的理论模型和基于Abel-Noble状态方程的数值计算模型，并分析初始罐内压力为34.5，70 MPa时H2泄漏问题，得到罐内H2滞止参数随时间变化曲线及出口气流速度与流量随时间变化曲线。

现有研究大都基于低压和恒定泄漏速率条件，但实际气体泄漏速率会随储罐压力、温度等参数变化而变化，且大多数气体存储设备压力均高于环境压力。当储存压力与环境压力之比大于气体临界压力比(vcr)时，气体泄漏就会产生欠膨胀射流。发生欠膨胀射流的泄漏口处速度会达到当地声速，离开泄漏口的气体会以超音速继续向外膨胀，最终在射流的远场区完全膨胀，气体流动完全发展。以某天然气储配厂为例，使用泄漏过程模型和等效喷嘴模型，利用FLACS软件对储配厂存储压力1.05 MPa高压天然气非恒定速率泄漏扩散过程进行数值模拟，考察环境风速、泄漏时间对天然气泄漏扩散的影响，为研究欠膨胀射流高压天然气泄漏事故，采取相应预防措施提供理论依据。

1 数学模型及参数设置

1.1 气体泄漏扩散数值模型及有效性验证

对于气体泄漏扩散，使用标准k-ε湍流模型，采用SIMPLE压力修正法算法，并将其推广到处理含附加源项的可压缩流动。通过建立描述流体特性的质量、动量、能量以及组分守恒方程，结合边界条件求解计算区域中超压、浓度、温度等变量值，湍流和化学反应影响包含在方程当中[12]，方程如式(1)所示：

(1)

式中：Sφ为源项；φ为通用求解变量，包括质量、动量、能量等变量；ρ为气体密度，kg/m3；xj为j方向积分；μi为i方向上速度矢量；Γφ为扩散系数。

FLACS数值模型经过多次改进与验证，其结果具有可靠性和有效性。

2004年，Hanna等选用Kit Fox实验、MUST实验、Prairie Grass实验及EMU的L型建筑物风洞数据集[13-17]，通过空气质量模型性能测量方法对FLACS气体泄漏扩散模型进行有效性验证。结果表明：FLACS的CFD模型可以很好地预测气体泄漏扩散情况，其结果具有可靠性和有效性。2010年，Hansen[18]利用实验数据(China Lake,Burro,Coyote)验证CFD模型，在不同大气条件下得到较精准的测量值和预测值。

1.2 等效喷嘴及泄漏过程模型

1)学者提出使用假设的低压泄漏源代替实际高压射流源。等效喷嘴模型基础原理源自Birch等提出的虚喷嘴模型，该模型可为气体泄漏扩散规律研究提供可靠气云分布数据。等效喷嘴模型假设：①气体以质量流量m从泄漏孔流出，从高压储罐内部到实际泄漏孔出口为等熵膨胀过程；②实际泄漏孔处气体流速为当地声速；③气体由实际泄漏孔流向虚拟泄漏孔过程满足质量守恒和动量守恒方程；④气体在虚拟泄漏孔处温度与压力已恢复到环境大气压与环境温度。

根据可压缩理论，确定实际泄漏孔处条件如式(2)～(4)所示：

(2)

(3)

(4)

式中：P1为实际泄漏孔处压力，Pa；P0为高压储罐内压力，Pa；γ为比热比；T0为储罐内温度，K；T1为实际泄漏孔处温度，K；Rn为气体常数，Rn=519.625 J·kg-1·K-1；ρ1为实际泄漏孔处气体密度，kg/m3；v1为实际泄漏孔处气体速度，m/s；c1为当地声速，m/s。

气体由实际泄漏孔流向虚拟泄漏孔满足质量守恒和动量守恒方程，如式(5)～(6)所示：

ρ1v1A1=ρ2v2A2

(5)

ρ1v12A1+A1(P1-P2)=ρ2v22A2

(6)

联立式(5)和式(6)可得虚拟泄漏孔处气体速度与直径，如式(7)所示：

(7)

式中：P2为虚拟泄漏孔处压力，该压力等于大气压力，Pa；v2为虚拟泄漏孔处速度，m/s；d1为实际泄漏孔直径，mm；d2为虚拟泄漏孔直径，mm。

2)过程模型

过程模型可根据储罐内初始压力、温度、储罐体积和泄漏孔面积计算不同时刻泄漏孔压力、温度等参数。高压气体泄漏过程分2个阶段：第1阶段是超临界流动状态，该阶段储罐内气体压力与环境压力比大于该气体临界压力比；第2阶段是亚临界流动状态，该阶段开始标志是储罐内压力降为该气体临界压力[11]。在第1阶段，储罐内气体压力(Pi)随时间变化如式(8)所示：

(8)

式中：常数如式(9)所示。

(9)

储罐内温度(Ti)随时间的变化如式(10)所示：

(10)

式中：Pi,0为储罐内初始压力，Pa；Ti,0为储罐内初始温度，K；vi,0为储罐内气体初始比体积，m3/kg。

由式(2)～(4)可得，实际泄漏孔处压力、温度、密度、质量流量等参数。因为C>0,γ>1，所以储罐内压力和温度会随时间增长而下降。

在第2阶段，泄漏孔处压力与外部环境压力相等，且不再随时间变化而变化。设该时间为ttrans，如式(11)所示：

(11)

由罐内气体质量与罐内压力(pi′)变化关系及气流质量流量(qm′)得式(12)：

(12)

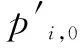
令

(13)

(14)

联立式(13)与式(14)，式(12)可简化为式(15)：

(15)

根据压力微分方程，最终可得储罐内气体压力(Pi′)和温度(Ti′)随时间的变化[19]，如式(16)所示：

(16)

泄漏孔压力为大气压力，即P1=Pa；泄漏孔处温度(T1)和质量流量(m)计算如式(17)～(18)所示[19]：

(17)

(18)

式中：Pa为大气压力，Pa；P1为泄漏孔处压力，Pa；A1为泄漏孔面积，m2；Rn=519.625 J·kg-1·K-1，为气体常数。

1.3 几何模型及参数设置

1)几何模型与网格尺寸

以某天然气储配厂为例，对罐区高压天然气泄漏进行数值模拟。该储配厂面积240 m×170 m，储配厂天然气球型罐共4台，压力1.05 MPa，各储罐最大充装系数0.8，依据现场实际情况按1∶1大小建立几何模型。总计算区域扩大为280 m×210 m×50 m，为保证计算精度，节省计算时间，对泄漏点周围网格进行加密，在核心区域(60 m×90 m×20 m)采用大小一致立方体网格，在细化网格与均一网格之间使用光滑(Smooth)命令处理，对核心区域外网格进行延伸处理，延伸比例小于1.2。根据FLACS软件网格设置指导[12]及网格独立性分析，设置气体泄漏核心区域立方体网格尺寸为1 m，细化区域网格大小为0.35 m，网格X、Y、Z方向的相邻控制体厚度递差均为20.29%，满足FLACS软件计算网格要求。最终几何模型及网格划分如图1所示，网格单元约49万个。

图1 几何及网格模型Fig.1 Geometric and mesh models

2)泄漏速率计算及参数设置

由于天然气储罐初始压力为1.05 MPa，由式(19)可得，环境压力与储罐内滞止压力之比小于甲烷的临界压力比，发生泄漏时将产生欠膨胀射流。

(19)

式中：甲烷比热比γ取1.3。

为研究较严重泄漏场景，泄漏孔径设定100 mm。由式(1)～(3)可得实际泄漏孔处初始泄漏质量流量15.54 kg/s；由式(4)～(6)可得初始虚拟泄漏孔直径345.86 mm；结合过程模型，在T=200 s时，质量流量14.83 kg/s，虚拟泄漏孔直径336.49 mm。在T=7 558 s时，气体泄漏进入亚临界流动状态，泄漏质量流量降为3.11 kg/s。质量流量随时间变化曲线如图2所示。

图2 质量流量随时间变化关系Fig.2 Change of mass flow rate with time

结合模型及现场实际情况可知，储罐上部与下部容易发生泄漏。天然气主要组分为甲烷，密度比空气小，当储罐上部发生泄漏，气体随泄漏初始动能与空气作用向下风向和更高处扩散，且高处出现点火源的可能性较小，所以本次泄漏位置选储罐底部，泄漏方向为+Y方向，泄漏工况见表1。参考厂区所在地区气象条件，设置风向45°。根据风向及FLACS软件指导手册，设置X，Y，Z正边界条件为Wind，负边界条件为Nozzle。

表1 泄漏工况Table 1 Leakage conditions

2 泄漏模拟结果分析

2.1 风速及泄漏时间对可燃气云分布的影响

不同风速条件下T=200 s时可燃气云分布3维视图如图3所示(甲烷体积分数为5%～15%)。由图3可知，气体泄漏后在近场区受初始动能主导，从高压储罐泄漏的天然气，本身具有很大动能，即使使用虚拟泄漏孔代替实际泄漏孔，在虚拟泄漏孔处初始泄漏速度也能达239.97 m/s，初始动能447.44 kJ。在初始动能主导下向泄漏方向扩散时，随扩散距离增加，需克服风力等阻力，动能逐渐减小，在距离泄漏源较远区域，气云受风力和浮力作用才开始显现。通过对比不同风速条件下气云分布可知，自然风速增大可有效减少可燃气云分布区域，减小可燃气云体积。

图3 可燃气云分布3维视图(T=200 s)Fig.3 3D view of combustible gas cloud distribution(T=200 s)

当T分别为10，100，200 s时，对应风速条件下离地面1.5 m处XY平面可燃气云分布如图4所示。为研究风速对可燃气云分布的动态作用，分析同等高度下，不同时间对应不同风速条件下可燃气云分布最长距离，统计结果见表2。

图4 不同时间对应不同风速条件下XY平面可燃气云分布Fig.4 Distribution of combustible gas cloud on XY plane at different time and different wind speeds

由表2可知，同等高度条件下，风速越大，可燃气云在Y方向扩散距离越短；在X方向，由于风向与气体泄漏方向不一致，气云随风速增大，扩散最远距离先增大后减小。从时间角度分析，可燃气云在T为10～100 s，扩散最长距离变化明显，但在100～200 s扩散过程中，可燃气云最长扩散距离变化不明显，最大变化距离1.76 m。结果表明，泄漏持续一段时间后，泄漏时间增加对可燃气云分布影响较小，因为从第2节泄漏质量流量计算结果可知，持续泄漏200 s内，泄漏质量流量仅变化0.71 kg/s，对泄漏扩散影响不明显，所以各风速条件下高压天然气变速泄漏扩散会受风力作用及浮力作用，使气体扩散在一定时间内达到动态稳定；在相同泄漏速率下，风速增大可缩短气云趋于动态稳定时间，风向对于泄漏扩散的影响越来越明显，泄漏气体会有明显往下风向扩散的趋势。

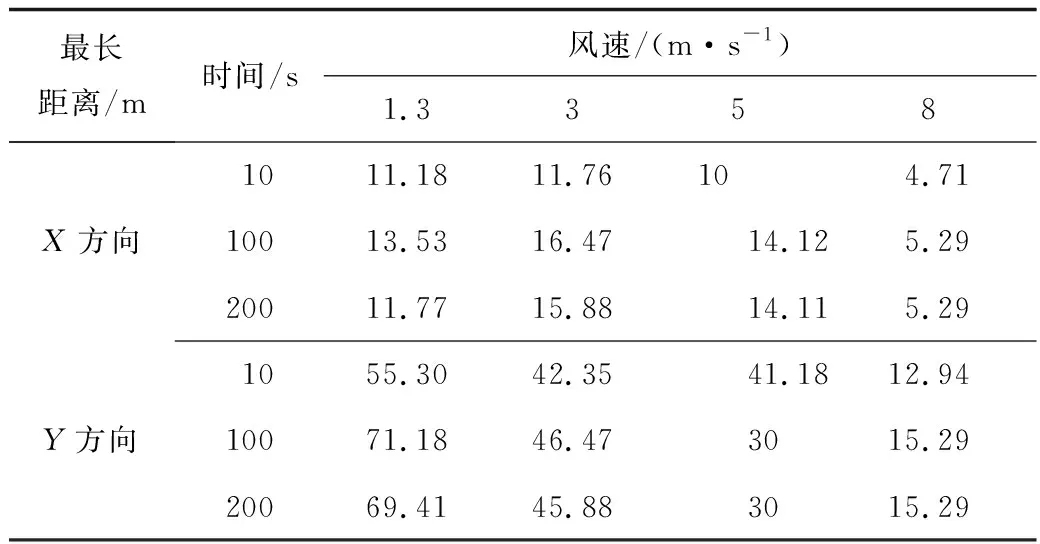
表2 不同时间对应风速条件下可燃气云分布最长距离统计Table 2 Statistics on longest distance of combustible gas cloud distribution at different time and different wind speeds

2.2 风速及泄漏时间对真实气体等效化学计量气云体积的影响

等效方法可在模拟次数最少情况下得到爆炸载荷的均匀分布。分析等效化学计量气云体积，对爆炸研究意义重大。在FLACS中用于评估爆炸后果的等效化学计量云有9种，其中Q8和Q9较为常用：Q8主要用于阻塞度较高的场景，Q9主要用于阻塞率低，通风良好的开放场景。本文模拟场景为天然气储罐区，四周空旷，所以选择Q9进行分析。Q9表达公式如式(20)所示[20]：

Q9=∑V×BV×E/(BV×E)

(20)

式中：V为可燃气体体积，m3；BV为层流燃烧速度，m/s；E为在空气中恒压燃烧所产生的体积膨胀。

图5 不同风速条件下等效化学计量云体积Fig.5 Equivalent stoichiometric cloud volume under different wind speeds

4种风速条件下等效化学计量云体积如图5所示。由图5可知，风速为1.3 m/s时，等效化学计量气云体积在60 s后不再发生明显变化，在200 s时达到575.87 m3；风速为3 m/s时，等效化学计量气云的体积在40 s之后变化不明显，基本稳定在330.68 m3；风速为5.0,8.0 m/s时，在15 s之后分别稳定在184.69，104.19 m3。结果表明，在持续泄漏的200 s内，真实气体等效化学计量气云体积在气体泄漏初始动能、稳定风场及浮力共同作用下，一定时间后趋于稳定；在持续泄漏的200 s内，达到动态稳定状态后，泄漏时间增加对等效化学计量气云体积几乎无影响。

3 结论

1)储存压力为1.05 MPa天然气储罐发生泄漏将产生欠膨胀射流，根据等效喷嘴模型，使用虚拟泄漏孔代替实际泄漏孔，泄漏初期仍具有447.44 kJ的高动能，气体泄漏扩散在近场受初始动能主导。

2)结合过程模型，在持续泄漏的200 s内，气体泄漏质量流量仅产生0.71 kg/s变化，对气体泄漏扩散影响不明显；该时间段内，不同风速条件下高压天然气变速泄漏，并在初始动能、稳定风场及浮力共同作用下，使可燃气云体积及分布在一定时间内达到动态稳定状态，等效化学计量气云体积不再发生明显变化；风速增大可缩短动态稳定时间；随泄漏时间进一步增加，质量流量会有明显变化；当T=7 558 s时，气体泄漏将进入亚临界流动状态，质量流量下降为3.11 kg/s，相比初始泄漏流量减少12.43 kg/s。

3)风速对可燃气云分布和体积影响较明显；相同泄漏速率下，可燃气云分布范围和体积随风速增大而缩小，风速变大会增大风向对气云扩散的影响。