基于混合算法的需求响应公交灵活调度模型

靳文舟 胡为洋 邓嘉怡 罗晨伟 韦兰辉

(1．华南理工大学 土木与交通学院，广东 广州 510640；2．广州市交通规划研究院，广东 广州 510230)

随着国民经济的飞速发展，人们生活水平不断提高，对交通出行提出了新的要求。然而，当前交通服务方式较为老旧单一，难以最大化利用资源满足乘客需求。同时，大城市公交运营模式无法有效兼顾运营的经济性和服务水平。因此，在城市公共交通的理论实践基础上，应当进一步开发细化不同类型的公交模式，创新出多元优质的新模式，继续深化城市和乡镇公共交通的供给侧改革，在兼顾经济性的同时全面提高公共交通的竞争力。需求响应公交(DRT)是一种预约式定制化的公交服务模式，一般应用在不适合常规公共交通服务的地区，如人口密度较低的城镇、郊区或者农村地区。目前的DRT理论还不够完善，部分理论不能直接应用于实际，并且我国的农村贫困地区有独特的地理形态，部分外国的研究并不适用。因此，有必要研究适用于我国多数城镇农村的公交调度新模式，即考虑多种车型和多种运营模式的公交灵活调度模型。

公交灵活调度是根据乘客需求量来决定车型和运营模式(直达或者接驳)，其中求解的问题可归为多车场多目的地的车辆路径问题(VRP)。在以往的研究中，多数研究将实际问题简单化处理，通常是考虑单一的车型或单一的运行模式。Daganzo[1]首次提出了可变线公交的概念。Cortes等[2]提出了一种比传统公交系统更具竞争力的公交替代方案即DRT系统，并进行了仿真分析，认为DRT系统可以以更优的成本运营。熊杰等[3]在量化研究基础上分析了基于社区公交的路径优化的需求响应型公交，以最大化路径需求潜力为目标建立目标函数，用改进的遗传算法对 DRT 社区公交调度模型进行求解。邱丰[4]提出了一种两阶段车辆调度模型,以满足实时动态调度的需要，并借助模拟退火算法及启发式插入算法处理当前及预先需求。Golden等[5]率先研究了多车型车辆路径问题，并采用改进的旅行商问题(TSP)和节约算法对多车型VRP进行求解。国内针对多车场问题提出了各种编码方式和模型。邹彤等[6]采用染色体基因组序列来求解多车场问题。叶志坚等[7]分析了5种求解多车型VRP的启发式算法的优劣势，提出了几种混合启发式算法。马建华等[8]建立了最快完成配送的多车型多车场车辆路径问题的模型，并采用变异蚁群算法来求解该问题。罗鸿斌[9]设计了用于求解多车场多车型车辆路径问题的改进粒子群算法，可以防止算法局部收敛。

从这些研究可以看出，目前国内外学者对公交接驳公交这种公交组合调度的研究较少，大多研究是在需求响应公交接驳轨道交通上深入挖掘，国内少数对需求响应公交协同调度的研究只针对单一接驳模式的运营方式[10- 12]，并且这些研究对客流量和车场位置都有严格的要求和假设，在应用于实际方面有一定的困难。因此，本文提出了考虑多种车型和多种运营模式并行的需求响应公交灵活调度模型，采用大循环小循环混合模式设计了新的混合遗传蚁群算法，并采用该算法来求解公交灵活调度的最优路径，最后通过实例分析该模型的可操作性和科学性。

1 公交灵活调度模型

1.1 多车型多调度模式调度场景

现有的DRT应用场景较多[13- 15]，本文研究中多车型和多调度模式是在不同客流量下采用的不同调度模式，其核心就是根据不同客流量采用不同的调度模式，如图1所示。其中低客流、中等客流、大客流是大致的客流范围描述，具体区分和定义需要根据整个模型的计算来划分。

(a)低客流情形下

(b)中等客流情形下

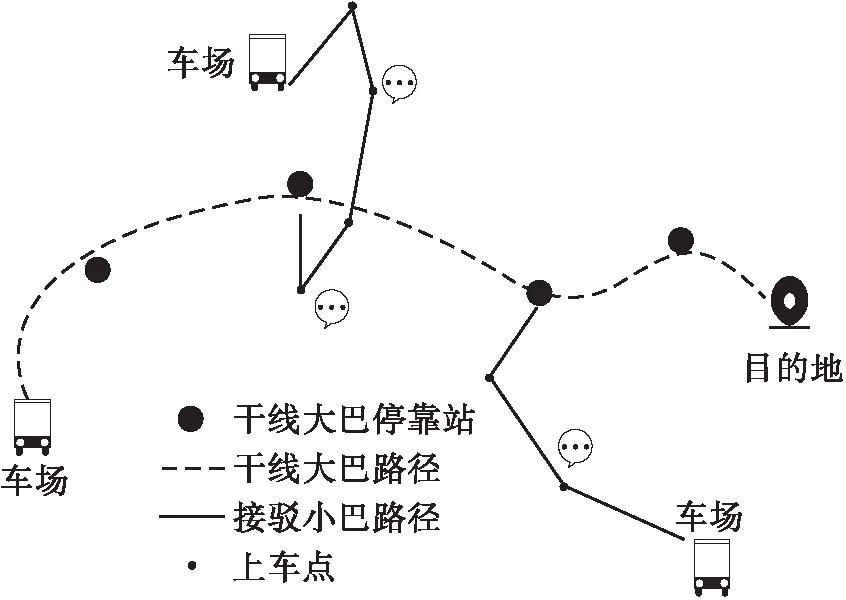
(c)较大客流且需求分散情形下

理论上公交灵活调度模型的3种典型应用场景如下：

(1)在客流较低的情况下，需求较少，调度平台采用小巴即可满足所有乘客的出行，系统采用小巴直达调度的方式。

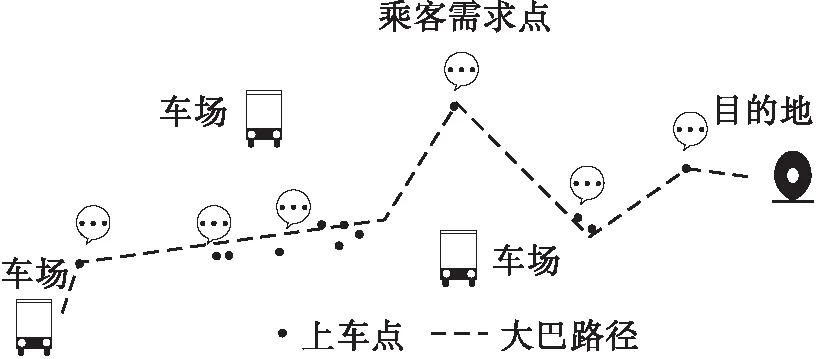
(2)在客流中等的情况下，调度平台只采用小巴无法满足运营需求且成本较高时，系统采用大巴直达调度的方式。

(3)在出行客流高峰期时，采用直达方式就会导致成本的上升，并且也无法解决大客流和需求点过度分散等问题。在此情形下，DRT联乘接驳模式就有很强的优越性，其主要思想是干线大客流采用大型巴士，支线采用接驳方式将部分乘客接驳到干线巴士的中途站点乘坐干线巴士到达目的地。

1.2 模型的构建

首先，在乘客预约的需求点的分布基础之上，通过不同车型的选择来控制调度模式的选择，在选择车型后会抉择出对应的调度模式。选择单一车型时，采用直达车的调度方式，根据运营需求，做出对应的约束条件；选择两种车型时，采用联乘调度方式，先根据需求点的分布，采用聚类方法聚类需求点，确定干线车的中途停靠站点，根据联乘模式的特殊性，给出对应的约束条件。在此基础上，做出其他必要的约束，同时以运营总成本和乘客出行时间窗的惩罚函数的最小值作为目标函数，其中运营总成本考虑了固定成本和可变成本，以确保运营的可操作性和经济性。

1.2.1 模型假设

本文的公交灵活调度模型做出以下基本假设：

(1)所有的服务车辆都从固定站点(公交站场)发车，公交的全部发车点、全部乘客需求点、公交中途停靠点、目的地的位置信息是已知的。

(2)发车点车型有大巴和小巴2种，同时假设所有属于O集合的发车点车辆配置相同，v车型的车辆有Z′v辆车。

(3)车辆速度采用平均速度，车速恒定，不考虑外界、驾驶员和车辆本身等因素对车速的影响。

(4)车辆各停靠点均被服务且仅被服务一次，发车点、乘客需求点、干线大巴中途停靠点、目的地之间的距离均只考虑其空间直线距离。

(5)乘客的需求时间窗已知，乘客都准时到达等待，且上车、启动等损失时间相同。

(6)乘客会响应服务，不会拒绝乘车。

(7)车辆路径均是从发车点出发，到中途停靠点或者目的地后结束。

1.2.2 模型参数

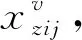
(1)

(2)

1.2.3 最优路径模型

以接驳巴士车辆固定成本C固、运输成本C变和时间窗惩罚函数f(T)的和最小作为目标函数，建立DRT接驳巴士车辆最优路径模型：

minC=C固+C变+f(T)

(3)

(4)

(5)

(6)

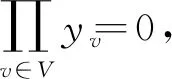
灵活调度模型的约束条件有:

(7)

(8)

(9)

(∀v∈V,∀z∈Zv)

(10)

(∀i,j∈O∪M∪T;∀v∈V;∀z∈Zv)

(11)

(∀i∈O∪P,∀v∈V,∀z∈Zv)

(12)

(∀i∈O∪P,∀v∈V,∀z∈Zv)

(13)

(∀j∈P)

(14)

(∀j∈P-Pm)

(15)

(∀j∈P∪M∪T)

ta(j)+ts(j)≤tb(j), ∀j∈P∪M∪T

(16)

(17)

(∀v∈V;∀z∈Zv;∀i,j∈O∪P∪M∪T)

(18)

(19)

(∀v∈V,∀z∈Zv)

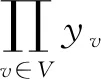
2 混合遗传蚁群算法

本文提出的混合遗传蚁群算法HGACO是将混合遗传算法HGA和蚁群算法ACO并用的一种混合遗传算法。蚁群算法是一种仿生算法，算法的灵感来源是蚂蚁群体寻找食物的行为，蚂蚁算法具有健壮性、搜索能力强、正反馈性、分布式计算等优点，已广泛应用于公交路径的求解[16]。将HGA和ACO算法融合，可以克服两个算法的缺陷，使HGA和ACO的优势互相补充，形成一种性能更好的混合算法[17- 20]。其中HGA是混合了近邻搜索算法、2- opt、目的地降维算子(多目的地选择时使用)的一种混合遗传算法。HGACO算法流程图如图2所示。

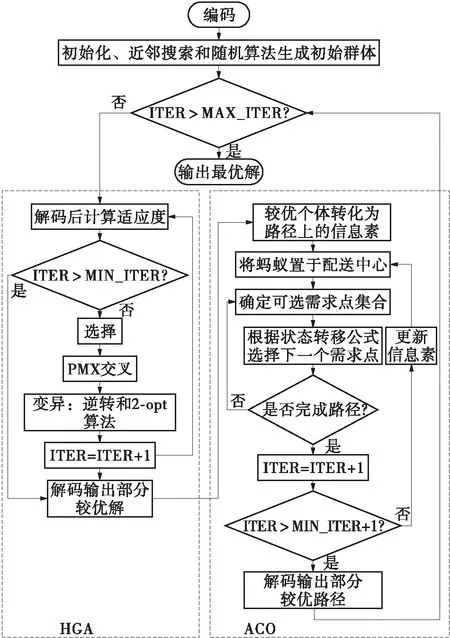
图2 HGACO算法流程图

本文提出的HGACO算法流程中有几个关键问题：①用近邻搜索算法构建部分初始种群，使相近的需求点排列在一起，生成最优解的可能性大大提高；另一部分种群中的个体随机生成，维持种群的多样化。②在变异时采用多次2- opt法和逆转变异进行局部路径优化。③采用不易收敛的最大最小蚁群算法(MMACO)。④两种算法的有机结合，本文根据大循环嵌套小循环的思路，在两种算法之间迭代，如令大循环次数为MAX_ITER，小循环次数为MIN_ITER，则表示先循环HGA至MIN_ITER，输出部分较优解给ACO，ACO循环迭代次数达到MIN_ITER后，再传递部分最优解来替换HGA的种群较差解，循环往复直至迭代次数到MAX_ITER。⑤在解码中内嵌了目的地降维算子，可以降维处理多目的地的VRP问题。这些关键算子和算法的融合提高了HGA的搜索能力和速度。

2.1 种群初始化

初始种群通过近邻搜索算法和随机生成两种方式得到。近邻搜索主要通过k-最近邻算法生成几个组团，其中可以将车场作为训练的样本中心，训练需求点生成以车场为中心的组团，寻优更加有针对性和准确。

调试发现，先采用近邻搜索产生40%的初步优化种群，再用随机算法生成60%的种群，这样的比例是较优的，因为该比例可以提高初始解的优秀程度，同时保证了种群的多样性和全局搜索性。该种群生成的方法既能保证获得多样化的初始种群，又能充分根据多车场问题做出对应的初始优化，有效加快算法的收敛速度。

2.2 变异操作

变异操作是维持种群多样化和防止算法过早收敛的关键操作，一般变异算子有逆序式、插入式等。本文采用2-opt启发式互换法作为第一变异策略，随机产生两个基因位置，将两个位置的数值互换；然后采用逆转算子作为第二变异策略。两个策略是依次进行的，每接受一次变异操作，都将个体解码并计算适应度的值，将变异后个体与父代比对，选择较优的进入下一步操作，变异示例如图3所示。

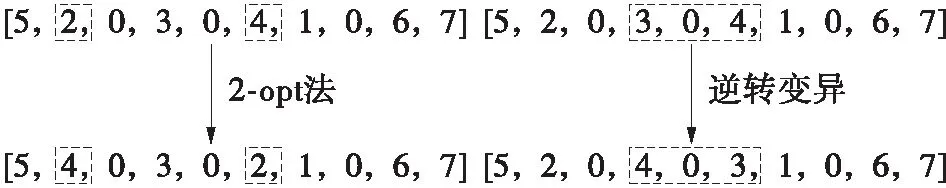
图3 变异示意图

2.3 改进的蚁群算法MMACO

经典的蚁群算法虽然有很多优点，但也有不少缺陷，如因参数设置不当或者数据较大时，算法很难求得最优解，非常容易陷入局部最优解和早熟。本文的改进蚁群算法采用了改进的MMACO算法，该算法是综合性能最优的仿生改进算法之一[21]，收敛性弱，搜索性强，刚好与遗传算法模块互相补充。

(20)

(21)

式中，n为蚂蚁的代数，fitness(n)为第n代蚂蚁的最优目标函数，ρ为信息素挥发系数。这种控制信息素的方法可以有效避免信息素过度集中在某些路径，并远远大于其他路径，从而导致算法不再继续搜索，陷入局部最优。

2.4 算法的衔接和信息互相传递

在将混合算法中遗传模块的数据传递给蚁群模块时，本文选取遗传算法倒数1-20代(根据MIN_ITER的值来取)群体中每代的最优个体转化为路径上的信息素，用于传递优秀个体的信息。具体方法如下：

信息素初始化在HGACO开始时设置，同时选择GA中部分代的优秀个体视为蚁群产生的最优蚂蚁，用来更新路径信息素。更新式为

(22)

另一方面，在将混合算法中蚁群模块的数据传递回给遗传模块时，遗传算法的精英策略可以有效保护并发挥最优个体的优势，因此本文选取蚁群算法所有个体中最优的那个个体作为精英个体,替换遗传算法群体中适应度最差的个体。

2.5 目的地降维算子

目的地降维算子是在原来的解码过程后添加的算子，用于选择一个合适的目的地。接驳小巴的目的地是干线大巴的中途站点，设中途站点的集合为M，那么这些中途站点的编号为cardO+cardP+m，∀m∈{1，2,…,cardM}，cardO为O集合中元素的个数，在解码后，用这些站点依次替换解码完成后的目的地。再求解路径的目标函数(成本值)，选择最小成本值的m站点替换当前目的地(当两个m代表的成本值相同时，选择标号大的，标号越大，越靠近终点)。例如，个体[8，5，2，11，8，3，11，10，4，1，11，9，6，7，11]代表的4条路径分别为8→5→2→11，8→3→11，10→4→1→11，9→6→7→11。假设M=3，这3个站点的编号依次为11、12、13，用这些站点替换原来的目的地，结果如图4所示。

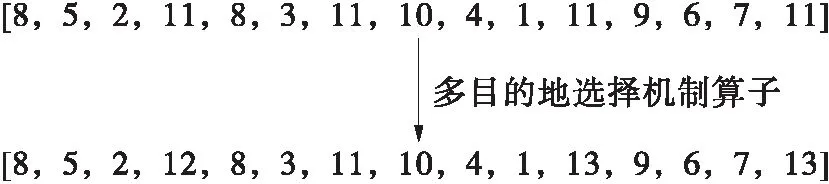
图4 目的地降维算子示意图

3 实例分析

3.1 数据获取和预处理

本次实验为验证公交灵活调度模型的可操作性和科学性，用早高峰、正午平峰、下午高峰3个时段的乘客数据作为研究对象，选取3个时段的数据比单一时段数据更具有一般性和代表性。实验通过互联网媒介、实地调研以及电话访谈等方式从揭西南部地区获得原始乘客数据，并使用AutoCAD按1：300 的比例尺将坐标转换为300 m/单位坐标距离。得到3个时段乘客位置数据如表1-表3所示。

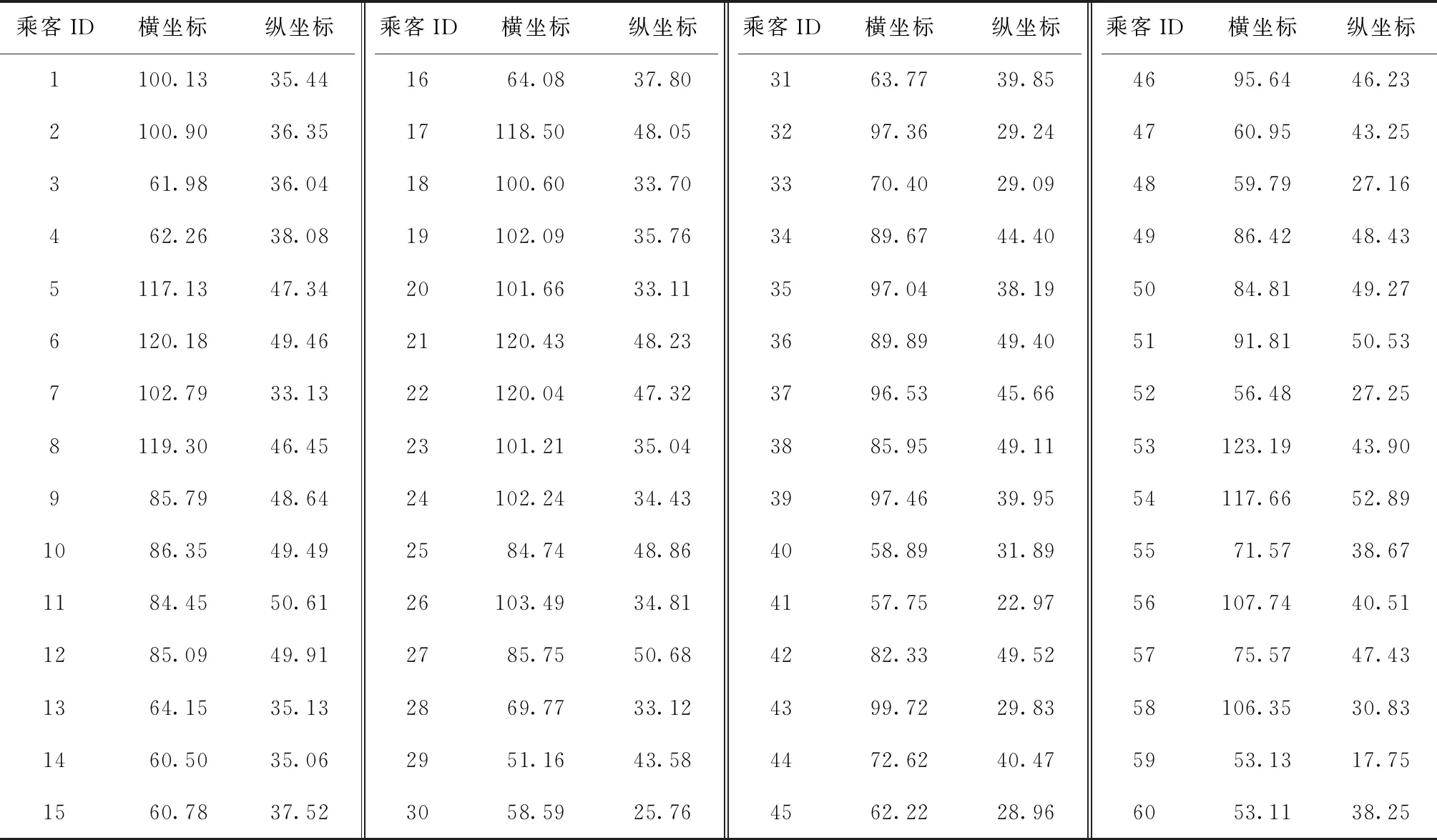
表1 早高峰乘客需求点位置

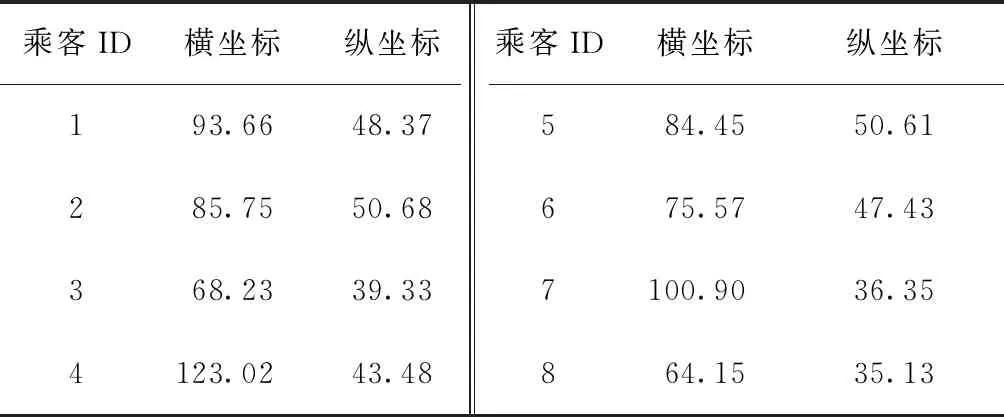
表2 正午平峰乘客需求点位置

建立虚拟车场一个，实际车场有4个(O1、O2、O3、O4)，目的地有一个，通过数据进行聚类，结合实际公交停靠站，得出中途停靠站有4个(M1、M2、M3、M4)，如表4所示。

原始数据不能直接用于模型的求解，若选择直达模型，可以将数据直接用于求解路径；若选择联乘模型，则需要将数据进行预处理：需求点Pi与中途站点M的距离为di(Pi,M)，需求点Pi与车场O的距离记为di(Pi,O)，乘客需求点筛选机制为

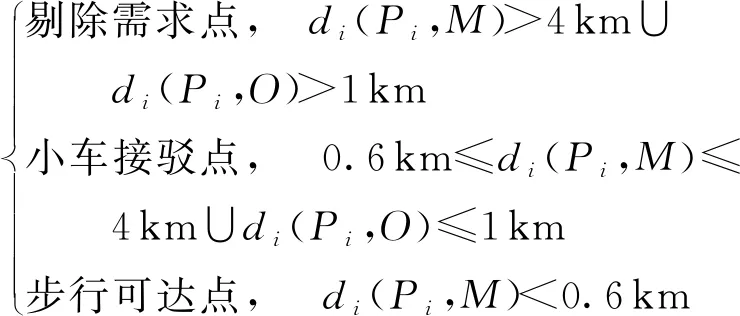
(23)

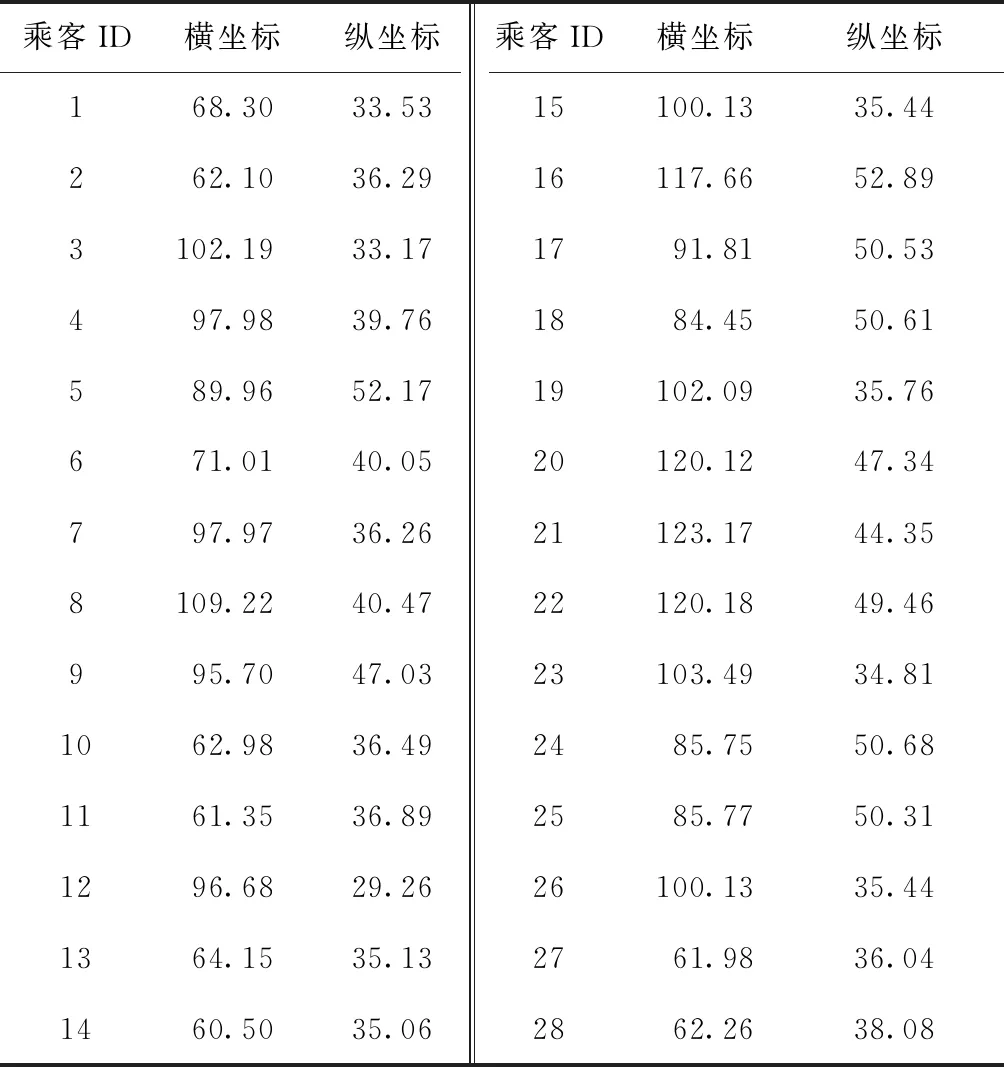
表3 下午小高峰乘客需求点位置

表4 车场和停靠站位置

筛选乘客需求点并归类，结果如图5所示。

图5 联乘调度下乘客筛选示意图

3.2 模型求解

模型求解中3个时段的数据集求解方式相同，本文以最大的数据集早高峰求解为例给出详细说明。

已知车场共有15辆车(13辆小巴，2辆大巴)，大巴起步固定成本定为15元，实际运营中的变动成本设定为1.2元/km，转换坐标为0.36元/单位距离，最大载客人数定为35；小巴起步固定成本定为5元，实际运营中的变动成本设定为1元/km，转换坐标为0.3元/单位距离，最大载客人数为6。

3.2.1 联乘调度模式的求解

根据乘客需求点的筛选规则，将不满足响应的需求点剔除后，再将可步行到达中途站点和需要接驳的乘客归类整理。

(1)长线大巴路径求解

由于长线大巴路径较为简单，故直接采用HGA算法求解，参数如下：种群规模NIND=30，精英策略GGAP=0.9，交叉概率PC=0.9，变异概率PM=0.1，MAX_ITER=60。设置好参数后，将中途站点、车场和目的地数据输入，运行后结果如图6所示，路径编码是6→1→3→2→4→9，最优成本为50.40×2=100.80元(早高峰乘客较多，超过大巴最大核载量，需要两辆车齐发，因此是求解结果的两倍)。

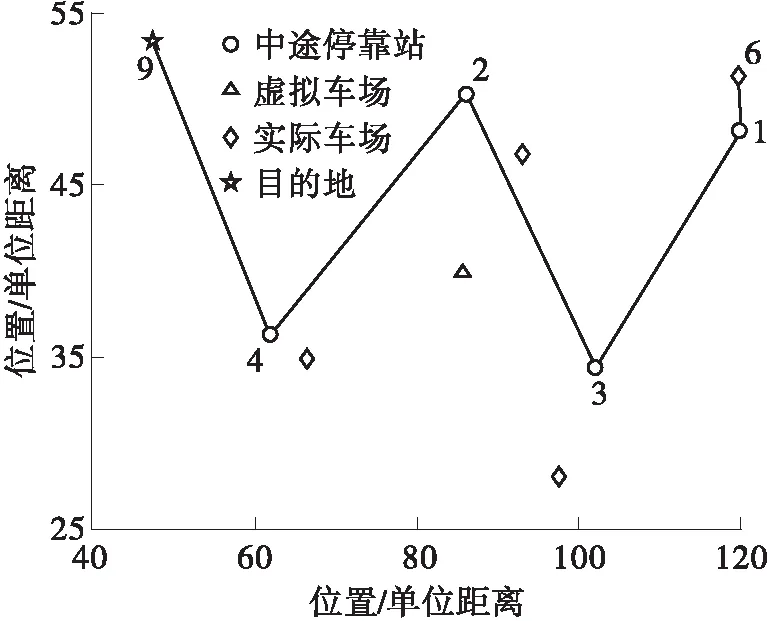
图6 早高峰时联乘模式下大巴路径示意图

(2)接驳小巴路径求解

输入需要接驳的乘客需求点(剔除可步行的乘客需求点)、车场、虚拟车场和目的地位置。设定HGACO算法的参数如下：种群规模NIND=200，精英策略GGAP=0.9，交叉概率PC=0.9，变异概率PM=0.1，信息素重要因子 Alpha=1，启发重要因子Beta=2，蒸发保留系数Rho=0.9，信息素增加强度系数Q=1，蚂蚁个数为50，车辆最大载人数CarQMAX=6，MIN_ITER=50，MAX_ITER=300。

多次运行后得到的最优结果如图7所示，路径编码是38→11→16→27→4→7→32→44，39→35→15→26→24→34→10→42，37→5→13→6→40，38→30→31→2→25→23→14→41，36→29→20→1→12→18→42，38→3→21→22→8→17→19→43，38→33→28→9→43；最优成本为100.47元。

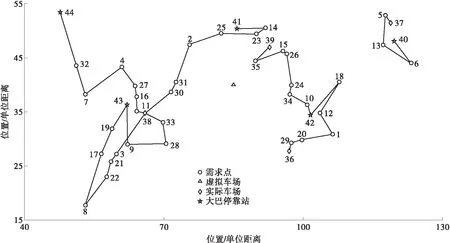
图7 早高峰时联乘模式下小巴路径示意图

3.2.2 直达调度模式的求解

由于乘客较多且较为分散，采用直达大巴“门到门”接送时延误较大，且路径的非直线系数过高，因此这里只采用小巴作为直达调度的交通工具。

由于乘客需求点较多，遗传算法的个体过长，无效染色体过多，求解效率较低，故本文采用最大最小蚁群算法求解。设定的MMACO算法参数如下：信息素重要因子Alpha=1，启发重要因子Beta=2，蒸发保留系数Rho=0.9，信息素增加强度系数Q=1，蚂蚁个数为50，车辆最大载人数CarQMAX=6，MAX_ITER=200。

多次运行后得到的最优路径编码是63→33→28→55→44→65，64→34→49→9→38→10→27→65，64→25→50→12→11→42→57→65，63→13→3→14→40→60→29→65，64→35→39→37→46→51→36→65，61→32→43→18→20→7→58→65，61→23→24→26→19→2→1→65，63→45→48→30→52→41→59→65，63→15→4→16→31→47→65，62→17→8→22→21→6→54→65，62→53→5→56→65；最优成本为253.64元。

3.2.3 结果分析

在早高峰的数据集下，采用联乘调度模式时，最优成本为大巴成本+小巴成本=100.80+ 100.47=201.27元；采用直达调度模式时，小巴直达的最优成本为253.64元。因此，在此数据集下，公交灵活调度系统选择联乘调度模式，车型选择为大巴+小巴，调度形式为采用小巴或步行让乘客到达大巴的中途停靠站，再由大巴将乘客接送到目的地。

同理，采用同样的思路求解数据集正午平峰和下午小高峰，结果如表5所示。从表中可知：本文模型的公交灵活调度场景得到充分的应用；在早高峰数据集下，乘客较多，公交灵活调度模型会选择小巴+大巴的联乘调度模式；在下午小高峰数据集下，乘客数量适中，公交灵活调度模型会选择大巴直达的调度模式；在正午平峰数据集下，乘客较少，灵活调度模型会选择小巴直达的调度模式。求解的结果表明，调度模式和车型的选择是由目标函数即最小成本决定的。本文的公交灵活调度模型具有科学性和可实践性。

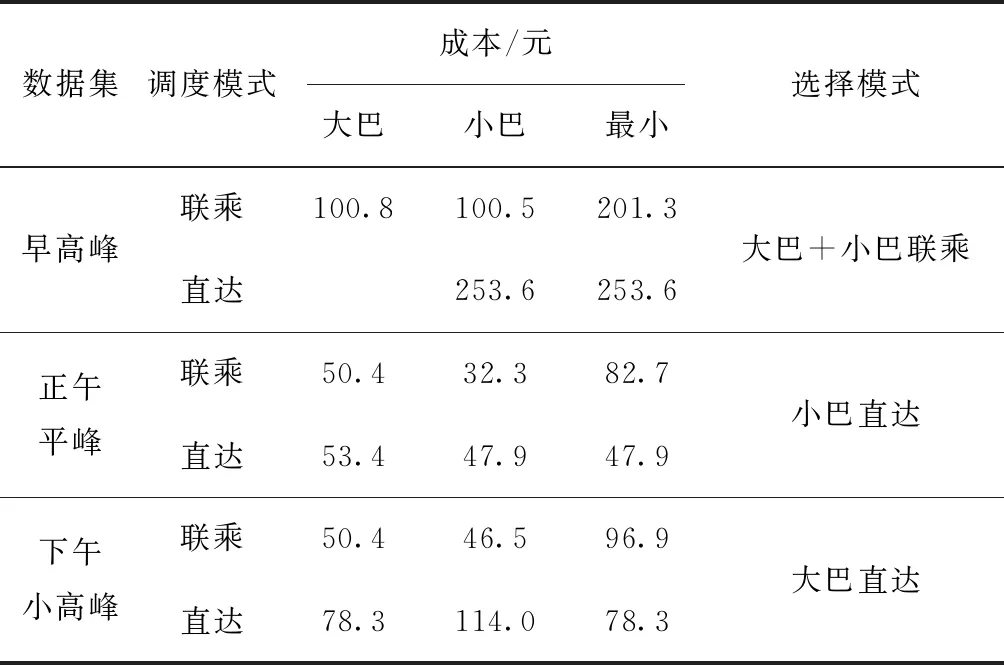
表5 不同数据集下的模型求解结果

3.3 算法性能分析

采用早高峰数据集接驳小巴路径的调度模式来分析混合遗传-蚁群算法HGACO与HGA(将HGACO算法的ACO模块去掉，其他混合算子不变)、MMACO的求解精度、求解效率、求解稳定性、求解速度。3种算法的参数设置相同：种群规模NIND=200，精英策略GGAP=0.9，交叉概率PC=0.9，变异概率PM=0.1，信息素重要因子 Alpha=1，启发重要因子Beta=2，蒸发保留系数Rho=0.9，信息素增加强度系数Q=1，蚂蚁个数m=50，车辆最大载人数CarQMAX=6 ，MIN_ITER、MAX_ITER分别为30、300。设置好参数，输入小规模算例数据，运行10次取平均，结果如表6所示。3种算法的迭代收敛曲线如图8所示。

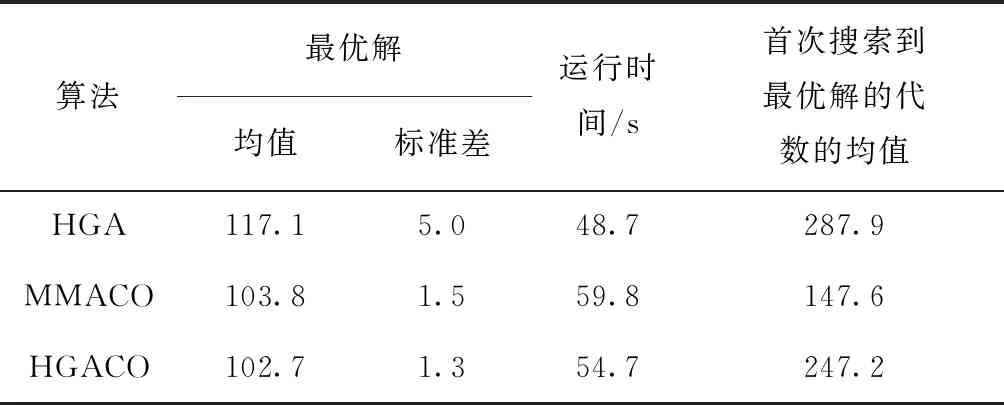
表6 3种算法的优化结果对比

从表6可知，HGACO算法的综合性能更优。HGACO 的最优解均值最低，说明HGACO算法的优化能力最强；HGACO算法的标准差最低，说明HGACO算法的求解优化结果更加稳定；运行时间方面HGACO算法较弱，处于中等水平，HGA算法的计算速度最快；在最优解的首次出现方面，MMACO算法最优。

从图8可知，HGACO算法在中后期的优化程度超过HGA和ACO算法，说明HGACO算法的求解能力较强，求解精度较高，优化结果稳定，具有一定的实操性和科学性。

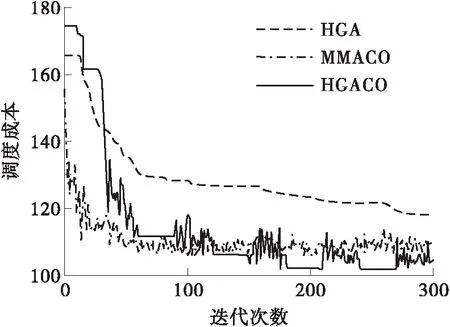
图8 3种算法的迭代收敛曲线

4 结语

本文针对DRT的灵活调度问题，提出了一种基于低密度人口稀疏地区的需求响应公交灵活调度方式，设立了车型和路径的双决策变量，并以此构建了考虑多种车型和多种运营模式的公交灵活调度模型；采用大循环小循环混合模式设计了混合遗传蚁群算法HGACO，在算法中通过加入目的地降维算子来解决起终点相异的多车场多目的地的车辆路径问题。实例分析结果表明：考虑多种车型和多种运营模式的公交灵活调度模型具有实用性和可操作性，该模型可以使低密度地区的需求响应调度更加科学和经济；改进的混合遗传算法HGACO的求解能力、精度和稳定性均优于原始算法，可以稳定地求得DRT灵活调度问题的较优解。