串并混联四足机器人腿机构的设计及运动学分析

马广英 王光明 刘润晨 姚云龙

(1.山东大学 机电与信息工程学院，山东 威海 264209；2.山东大学 力学与机电装备联合工程技术研究中心，山东 威海264209)

足式步行机器人拥有稳定性高、地形适应能力强等优点，具有广阔的应用发展空间[1]。腿机构是足式机器人的重要运动部件，其自由度、运动学和动力学以及空间位置变化等对四足机器人的运动具有决定作用。

现有的四足机器人腿机构大部分由串联机构组成，如BigDog[2]、Little Dog[3]、液压驱动四足仿生机器人[4- 5]和HyQ[6- 7]等。上述串联腿机器人控制简单，运动灵活，但承载力低[8- 9]。并联腿机构的优势在于刚度大、精度高、承载力大，工作空间范围小但稳定性优于串联腿机构[10]。如四足/两足可重组步行机器人[11]、3-RPC并联机构的新型步行机器人[12]、基于(U+UPR)P+UPS机构的并联机械腿[13- 14]和基于冗余驱动的并联机构机器人等[15]。

为了综合利用串、并联机构的优点，克服各自的不足，国内外学者对串并混联腿进行了研究。Ye等[16]提出了一种新型的串并混联机器人；周玉林等[17]将混联机构引入仿人机器人的研究；田兴华[18]等提出了3种混联腿部构型，并证实了混联腿的优越性。

随着四足机器人应用范围的推广，对机器人的运动灵活性和承载能力的要求越来越高。为了更好地发挥串并混联结构的优势，本文提出了一种新型的串并混联四足机器人腿部机构设计方法。首先利用螺旋理论分析了腿部机构的自由度，通过分析该机构位置得到运动学反解和正解方程，求解出该机构的驱动速度和加速度；然后通过机器人的腿部机构仿真，得到单腿运动的位移和速度变化情况，并通过ADAMS软件仿真结果与Matlab理论计算结果的对比来验证正反解模型的准确性；最后对腿部机构的工作空间进行分析，得到其足端的可达工作范围及运动特点，以验证该串并混联机器人的运动可行性及适应性。

1 R+{2-UPR+RPR}腿机构的结构

如图1所示，本文设计了一种具有R+{2-UPR+RPR}腿机构的串并混联四足机器人。整个基体与并联部分由R副联接，如图2所示。R副的轴线与上平台平行。并联部分由3条支链构成，其中两条支链各由一个U副(虎克铰)、一个P副(移动副)和一个R副(转动副)组成，另一条支链由两个R副和一个P副组成。由于其并联部分是主要研究对象，故简称其为2-UPR+RPR腿机构。相较于并联机构，该混联腿部机构的摆动幅度更大，工作空间更广。机器人进行步行运动时，串联部分带动整个并联部分进行转动；机器人进行避障工作时，并联部分各支链伸长或收缩，可以在保证机动性的同时提高承载力。

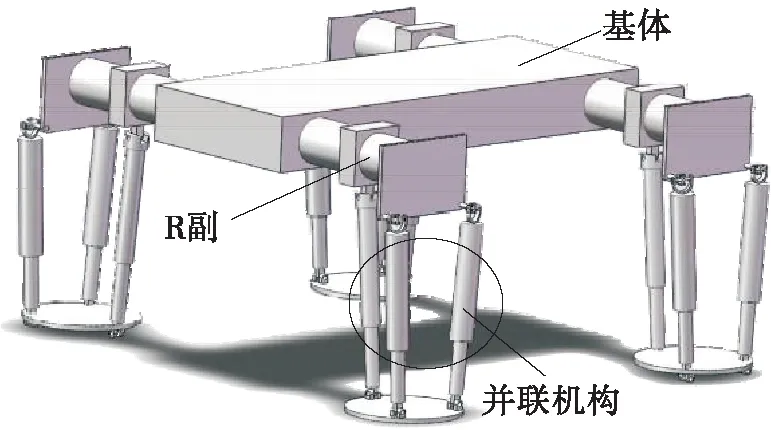
图1 R+{2-UPR+RPR}腿机构四足机器人

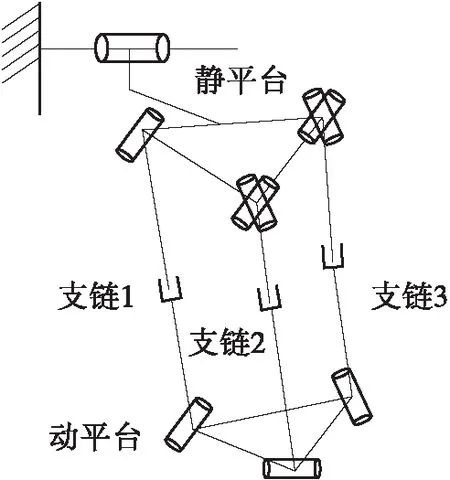
图2 腿部结构简图

2 四足机器人运动学分析

2.1 R+{2-UPR+RPR}腿机构的自由度计算

计算机构自由度常采用修正的Kutzbach- Grübler公式[19]：

(1)

式中，D为机构的自由度数，d为机构的阶数，n为机构包括机架在内的所有构件数，g为机构运动副数目，fi为第i个运动副的自由度数，ν为并联冗余约束数，ξ为局部自由度数。由于串联部分较简单，仅有一个转动副，自由度为1，因此，先使用式(1)计算并联部分自由度，再加上串联部分自由度，即可得到整个机构的自由度。

为了计算方便，取坐标系O-XYZ的位置如图3所示，点O是静平台三角形A1A2A3中A2A3的中点。基于螺旋理论，分别求得支链1、支链2和支链3的螺旋系与反螺旋系，并对反螺旋系再求其反螺旋系(二次螺旋系)，结果如表1所示。

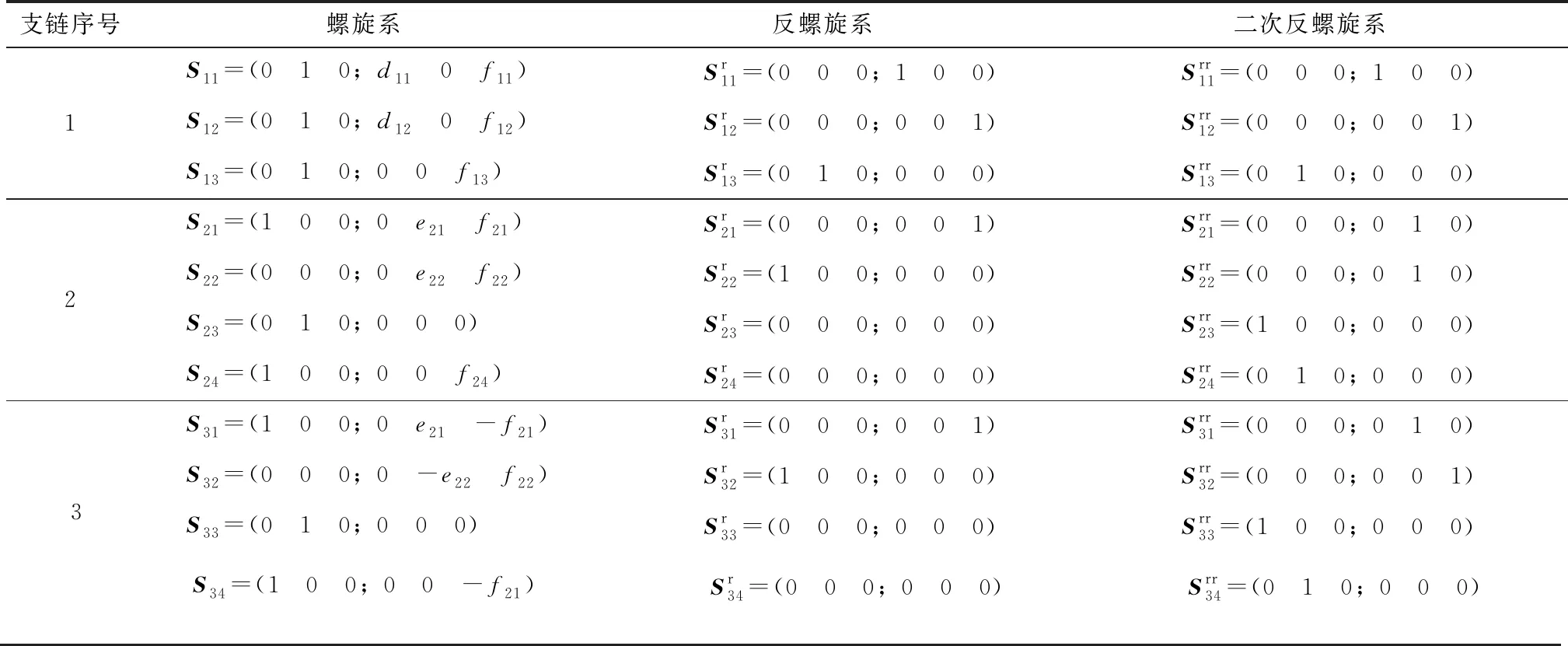
表1 并联机构螺旋系计算

图3 并联构型简图

将表1数据代入修正的Kutzbach-Grübler公式，可得M=2，故该并联机构具有2个自由度。由二次反螺旋系可以看出，并联机构能够实现的运动为绕Y轴的转动和沿Z轴的移动。再考虑串联部分，整个R+{2-UPR+RPR}腿机构具有3个自由度，包括绕X轴的转动、绕Y轴的转动和沿Z轴的移动。

2.2 R+{2-UPR+RPR}运动学分析

2.2.1 R+{2-UPR+RPR}运动学反解

由于该腿机构是混联的，运动学反解需要先求出足端所在的并联部分的运动学反解，并将此结果作为串联部分运动学反解的已知量，从而完成整个腿部机构的运动学分析。

为了简化计算，对腿机构的串联和并联部分分别建立如图4所示的坐标系。静平台A1A2A3和动平台B1B2B3均为等腰三角形，A1和B1为顶点，M、N分别为A2A3、B2B3的中点。在并联机构中，坐标系O-XYZ建立在静平台A1A2A3上，其中点O取在静平台的几何中心，即OA1=OA2=OA3；坐标系P-xyz建立在动平台上，P点取在动平台B1B2B3的质心。在串联机构中，坐标系R-XYZ建立在基体上，R点取在基体的几何中心。坐标系Q-XYZ建立在轴线垂直于基体的转动轴上，Q点取在串联部分转动轴线和OZ的交点处。4个坐标系对应的轴线方向互相平行，满足右手定则。

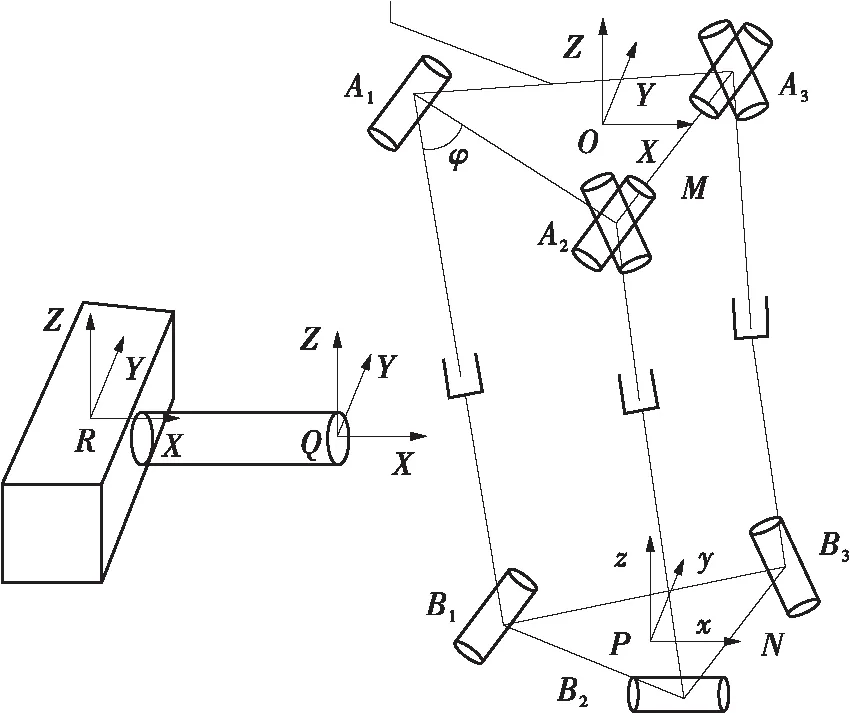
(a)串联机构 (b)并联机构

假设用Z-Y-X型欧拉角表示空间位姿，那么坐标系之间的变换矩阵可表示为

T=rot(z,α)rot(y,β)rot(x,γ)=

(2)

式中，XP、YP、ZP分别为P点在O-XYZ坐标系下X、Y、Z方向上的坐标。则在定坐标系O-XYZ下，Bi点的坐标可以表示为

(3)

(4)

(5)

利用该约束条件即可求解运动学反解。在本例中，运动学反解即为给定动平台位置ZP和动平台的姿态β，求腿支链A1B1的位移以及如图4(b)所示的腿支链A1B1与静平台的夹角φ。

(6)

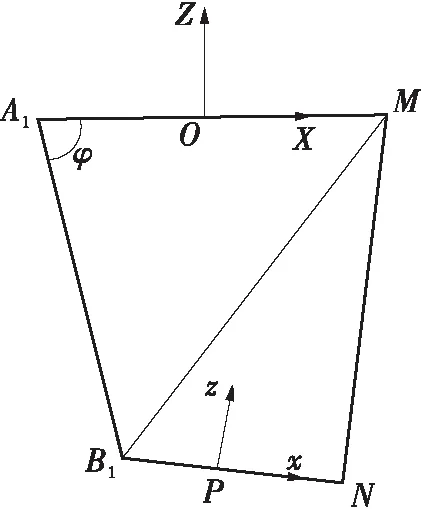
图5 平面A1B1NM

在如图5所示的三角形A1B1M中，由余弦定理得

(7)

进一步整理可得

φ=arccos{(a+b+ZPtanβ-dcosβ-esecβ)·

[(a+b+ZPtanβ-dcosβ-esecβ)2+

(8)

同理，使用欧拉角可描述串联部分坐标系Q-XYZ和坐标系R-XYZ之间的变化。为进行区分，这里使用α1、β1、γ1来代替欧拉角α、β、γ。由于此串联结构仅涉及一个旋转副，因此，坐标系Q-XYZ只能相对于坐标系R-XYZ的X方向发生旋转，即α1=β1=0。设转动轴相对于基体的转动角度为θ，则有

θ=γ1

(9)

综上，式(6)-(9)即为R+{2-UPR+RPR}腿机构的运动学反解。

2.2.2 R+{2-UPR+RPR}运动学正解

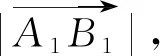
(10)

根据三角函数相关知识，可以得到并联部分的运动学正解方程组为

(11)

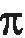
(12)

通过Matlab解方程组式(12)，可得到ZP和β的理论表达式，此即为R+{2-UPR+RPR}腿机构的运动学正解方程。

2.2.3 2-UPR+RPR并联机构运动学速度和加速度的求解

用雅可比矩阵来表示动平台的速度和驱动关节速度之间的映射关系，通过对反解表达式(6)-(9)的两边进行全微分求导，得到机构的雅可比矩阵。构造2-UPR+RPR并联机构驱动关节q1、φ、θ的速度方程式：

(13)

即

(14)

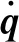
由式(14)可得

(15)

从而得到

(16)

式(13)对时间求导，得到加速度模型：

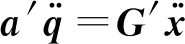
(17)

(18)

(19)

(20)

式(20)反映出并联机构驱动关节加速度间的输入输出关系，a称为并联机构的加速度矩阵，用Matlab软件对公式进行求解，得到相关参数。

3 仿真结果

3.1 运动学反解模型仿真

设动平台和静平台的参数分别为a=10.00 mm，b=11.70 mm，c=10.85 mm，d=10.47 mm，e=6.97 mm，f=8.00 mm。为求运动学反解和正解，对混联腿部机构规划一个周期为4 s、持续时间为8 s 的前摆动作，其足端的运动轨迹为

(21)

考虑到腿机构运动的实际情况，分别在串联部分转动轴、静平台转动副A1、杆A1B1施加主动驱动。根据式(5)-(9)和式(21)，得到电机转角θ、φ和杆长A1B1随时间的变化规律。将在Soildworks中设计的模型导入ADAMS软件，进行运动仿真。利用Matlab软件，代入运动学反解数学模型，数值计算得到该腿机构的驱动随时间的变化规律。运动学反解模型的仿真结果和理论计算结果如图6所示。从图中可知，理论计算结果与软件仿真结果的变化趋势相同，且误差很小，从而验证了运动学反解模型的正确性。

图6 运动学反解仿真结果与理论计算结果对比

3.2 运动学正解模型仿真

为了进行运动学正解仿真，规划一个周期为4 s、持续时间为8 s的前摆动作，其腿部的驱动运动轨迹为

(22)

将式(22)代入式(12)，得到腿机构并联部分的动平台绕X轴的转动角度γ1、绕Y轴的转动角度β、沿Z方向距离动平台的距离ZP随时间的变化规律，数值计算得到的结果同仿真结果如图7所示。从图中可知，理论计算结果与仿真结果的变化趋势相同，且误差很小，从而验证了运动学正解模型的正确性。

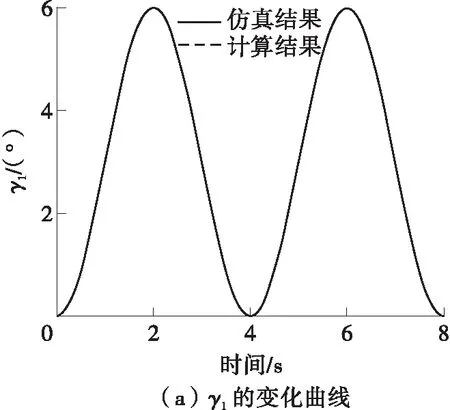
图7 运动学正解的仿真结果与理论计算结果对比

3.3 运动学速度、加速度模型仿真

根据建立的速度模型，将足端运动轨迹(21)代入驱动的速度模型和加速度模型，计算结果同仿真结果的对比如图8、9所示。从图8、9可知，速度和加速度变化量的理论计算结果与仿真结果的变化趋势相同，且误差很小，从而验证了运动学速度和加速度模型的正确性。

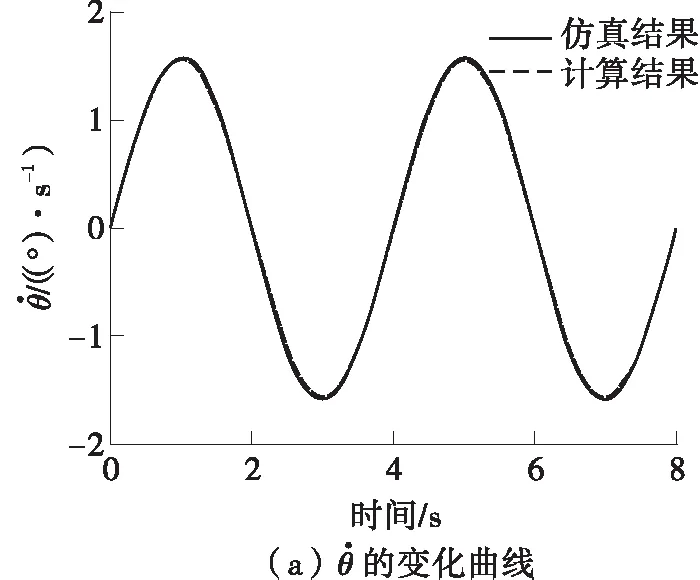
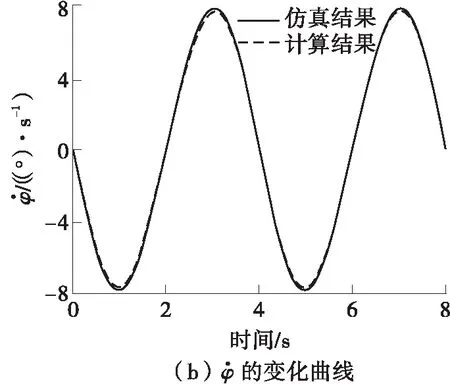
图8 运动学反解的速度变化的仿真结果与理论计算结果对比

3.4 单腿仿真运动

将运动学反解得到的驱动添加到腿部机构。单腿在8 s内实现两个周期的仿真运动。在初始状态时，单腿的足端处于着地状态。在0～2 s内，腿部按照既定运动轨迹抬起；在2～4 s内，腿部按照既定运动轨迹落下，单腿的足端着地，完成第一个周期内的运动；在4～6 s内，腿部按照既定运动轨迹抬起；在6～8 s内，腿部按照既定运动轨迹落下，单腿的足端着地，完成第二个周期内的运动。机器人的单腿仿真运动情况见图10。

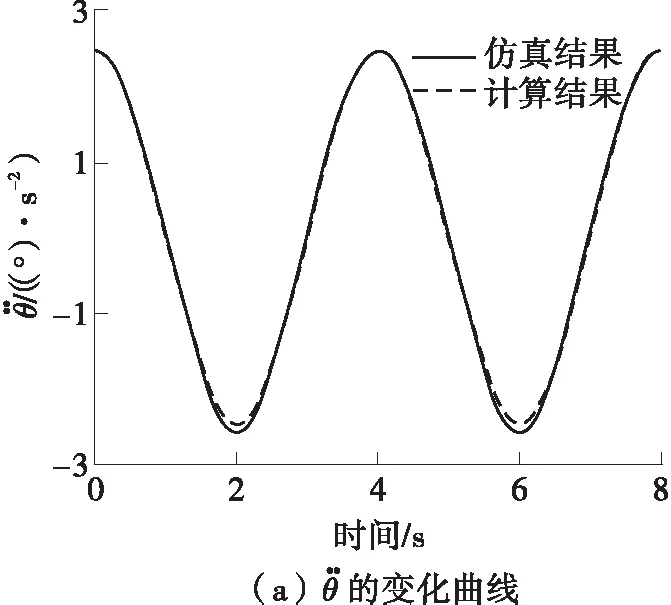
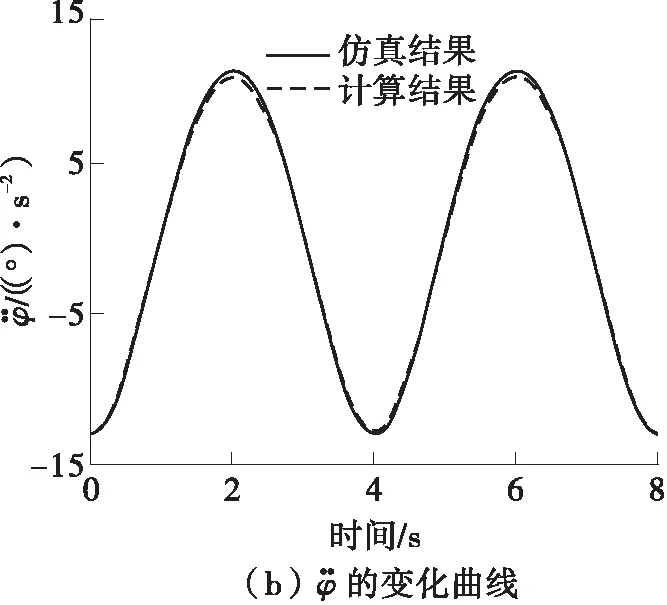
图9 运动学反解的加速度变化的仿真结果与理论计算对比

在施加驱动的基础上，得到足端机构在空间中的位移、速度变化曲线，如图11所示。从图像整体来看，足部机构的位移曲线平滑流畅，速度曲线无突变，运动稳定性高。当运动到2 s附近时，足部到达摆动极值点，此时出现短暂的匀速运动，保证了该腿机构进行往复运动，不会对机构构型造成破坏。在4 s附近，速度曲线过渡平稳，表明该机构可以进行稳定的循环运动。

图10 机器人单腿的仿真运动

图11 足端的位移、速度变化曲线

4 R+{2-UPR+RPR}腿机构工作空间

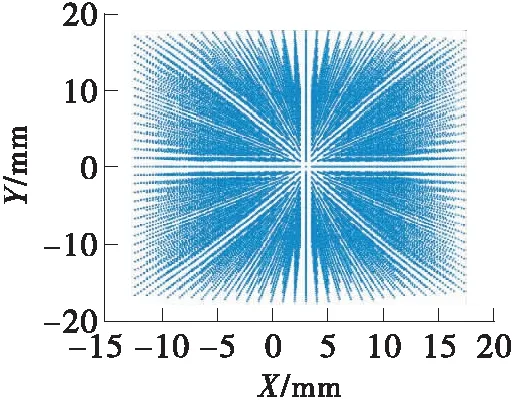
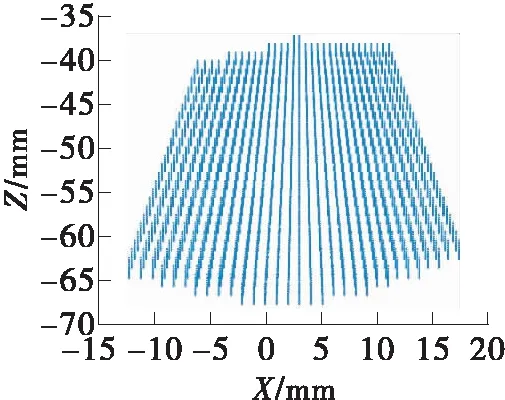
并联机构的工作空间主要包括可达工作空间、灵活工作空间和定姿态工作空间[19]。这里是利用搜索法找到R+{2-UPR+RPR}腿机构的可达工作空间。由于结构限制，R+{2-UPR+RPR}腿机构前后摆动幅度不会超过90°。利用Matlab软件，在-60 mm

(a)三维空间图

(b)X-Y方向投影图

(c)X-Z方向投影图

(d)Y-Z方向投影图

5 结论

本文提出了一种新型R+{2-UPR+RPR}腿机构，通过螺旋理论分析得到该机构的自由度情况。根据位置约束方程，对机构进行运动学反解和正解计算。根据运动学反解，求得驱动关节的位移、速度、加速度变化规律，并通过对腿机构运动的ADAMS仿真结果和Matlab软件理论计算结果的对比来验证运动学模型的正确性。对机构单腿的仿真结果表明，该机构运动平滑，无冲击特性。腿部机构工作空间的分析结果表明，该机构的运动空间连续、形状规则、摆动幅度较大，有较好的运动灵活性和工作平稳性，为进一步的动力学研究和步态规划提供运动学基础。R+{2-UPR+RPR}腿机构作为一种新型混联机构，兼具串联和并联机构的优势，可作为步行机器人腿部机构来实现资源探测、采样、危险环境救援等工作，具有较好的应用前景。