修形人字齿轮的润滑及摩擦特性分析

王延忠 徐梓淳 马涛 张亚萍 宋贯华 郝慧慧

(1.北京航空航天大学 机械工程及自动化学院，北京 100191；2.特种车辆及其传动系统智能制造国家重点实验室，内蒙古 包头 014030)

航空发动机是飞机的心脏，是决定飞机性能的重要因素。随着航空领域的发展，人字齿轮凭借其承载能力大、传动稳定性高、轴向力小等优点被广泛地应用在齿轮传动风扇发动机(GTF)中，其润滑性能的优劣对其抗胶合、抗磨损能力有直接的影响[1]。经过调查研究发现，从弹流润滑的角度对齿轮润滑特性展开分析是一种切实可行的方法。王延忠等[2]针对航空弧齿锥齿轮，在加载接触分析和点接触弹流润滑理论的基础上分析了齿轮啮合过程中的润滑特性变化规律。杨萍等[3]应用多重网格法求解斜齿轮的准稳态热弹流问题并将斜齿轮等效为两反向圆锥滚子。Pu等[4]基于表面粗糙度和卷吸速度夹角对混合弹流润滑模型进行改进，分析了弧齿锥齿轮的齿轮几何特征、运动学、混合润滑性能等。近年来，部分学者开始对人字齿轮的弹流润滑问题展开研究。Zhou等[5]基于流体非牛顿特性，分析了修形人字齿轮结构参数和工况条件对油膜轮廓曲线形状和位置的影响。Xiao等[6]针对修形人字齿轮瞬态非牛顿流体热弹流点接触问题，建立了法向和切向的油膜刚度和阻尼模型。

受齿轮结构等因素的影响，齿面接触压力、滚滑速度和滑滚比等参数在齿轮啮合过程中呈周期性变化，这种周期性变化的接触状态会造成齿面摩擦系数的时变性。目前，国内外学者分别从双盘、销盘、球盘实验[7- 10]和基于弹流理论数值计算两个角度出发，间接地测量和推导齿面摩擦系数。高创宽[11]建立了混合弹流润滑摩擦系数的计算模型，借助回归理论处理了大量计算结果并得出粗糙齿面的摩擦系数经验公式。Castro等[12]比较了双盘实验、全膜弹流润滑模型和混合弹流润滑模型对齿面摩擦系数的预测结果，得出混合弹流润滑模型评估结果准确的结论。Arana等[13]利用粗糙流体负载分配的方法对局部弹流润滑摩擦系数进行建模，实现了齿轮啮合过程中摩擦系数和功率损失的预测。上述研究证明了理论推导计算齿面摩擦系数的可行性。

本文在文献[5]分析鼓形修形对齿面曲率半径影响的基础上，逐步完成齿面的接触分析、齿面啮合点热弹流数值计算分析和齿面摩擦系数的时变特性分析，旨在通过这一计算过程直观地观察接触参数、油膜特征分布和摩擦系数在齿面上的变化规律；通过改变输入扭矩、主动轮输入转速和修形量，分析了工况条件和几何参数的变化对油膜轮廓曲线的影响。

1 人字齿轮齿面接触分析

齿轮的传动伴随着噪声、变形，啮入啮出时的冲击会引起速度及载荷的较大波动，这些因素均在一定程度上降低齿轮的动力学性能。齿轮修形是解决这类问题的一种直观、有效的方法，可根据实际工况和需求，在标准齿轮轮廓的基础上有目的地去除部分齿面材料。从优化齿面受载角度出发，确定鼓形修形作为本文人字齿轮的修形方法。鼓形修形可有效地降低不对中引起的传动误差，减小齿轮啮合时的噪声及振动[14]。以图1中人字齿轮单齿为例，将原有渐开线齿形修整为鼓形，定义修形量为20 μm。人字齿轮基本结构参数如下：主动轮齿数Z1=44，从动轮齿数Z2=41，法向模数mn=3.5 mm，法向压力角αn=22.5°，齿轮齿宽B=60 mm，螺旋角β=28.019°。基本计算工况为：输入扭矩M1=80 N·m，主动轮转速n1=300 r/min。

图1 鼓形齿面

本文从几何角度对齿轮每一啮合状态的受力情况展开分析。齿面接触线的长短在齿轮啮合过程中是时变的，其长度及位置变化决定了齿面受力、曲率半径等相关参数的变化。因此，对时变接触线变化规律的研究是人字齿轮接触分析的基础。由于人字齿轮的特殊结构，可在等效工况下分析单侧人字齿轮(斜齿轮)的齿面啮合状态，进而得到齿面接触参数的变化规律。

(1)时变接触线

从图2所示的啮合区端面可以看出，接触线主要分布在实际啮合区中，单条接触线在啮合区B2B1的长度不是定值，而是随时间变化的变长度线段，即单侧人字齿轮(斜齿轮)在啮合过程中每条接触线是时变的。受齿轮重合度的影响，实际啮合区中存在多条时变接触线，接触线总数与啮合齿数呈相似的数量变化规律。接触线在端面之间的距离满足如下关系：

pbt=L0/εα

(1)

式中，pbt为端面基节，L0为实际啮合区的长度，εα为端面重合度。

图2 啮合区端面

端面重合度εα和轴向重合度εβ的大小关系导致单侧人字齿轮(斜齿轮)的啮合过程和几何特征有所不同，从而使实际啮合区内接触线呈现出不同的变化特征。当εα>εβ时，第i对轮齿啮合产生的时变接触线的变化情况如图3(a)所示，计算式为

(2)

当εα<εβ时，时变接触线的变化情况如图3(b)所示，计算式为

(3)

式中，βb为齿轮基圆螺旋角。

图3 不同重合度关系下的时变接触线变化

通过计算发现本文的人字齿轮的εα<εβ，表明接触线在实际啮合区的变化为第二种情况。以一条接触线为研究对象，将其完全进入-离开实际啮合区视为一个计算周期。在一个计算周期内，对实际啮合区内的所有时变接触线长度求和，即可得到接触线总长：

(4)

式中，n为啮合区内时变接触线数量。

由式(3)计算可得一个计算周期内单条时变接触线的变化规律，如图4所示，在此区间内取3个有代表性的啮合点作为分析对象。Si(i=1,2,3)为计算周期内对应时刻所选取的啮合点，也代表啮合点所对应的主动轮旋转角度位置，分别为啮入侧啮合点S1、节点S2和啮出侧啮合点S3；主动轮旋转角度用θ表示。

图4 一个计算周期内单条时变接触线的变化

(2)曲率半径

基于本文时变接触线的变化规律,在啮合区内建立图3所示动态坐标系，y轴与时变接触线重合，x轴垂直于时变接触线，z轴垂直于啮合区平面。当接触线处于图4中的J1J2和J2J3阶段时，x′方向的曲率半径可表示为

(5)

当接触线处于J3J4阶段时，x′方向的曲率半径可表示为

(6)

推导得到x方向不同齿面的曲率半径：

(7)

则x方向的当量曲率半径为

(8)

y方向的当量曲率半径取决于齿宽、鼓形修形量Cα和螺旋基角的大小[5]，计算式为

(9)

(3)卷吸速度

将啮合齿面展开，可形象地表示卷吸速度方向，图5中Ue即为卷吸速度，其计算公式为

Ue=(U1+U2)/2

(10)

(11)

式中，ωi和Ui(i=1,2)分别为主、从动轮的角速度和主、从动轮啮合点的切向速度。

图5 齿面卷吸速度方向

(4)法向接触力

对单侧人字齿轮(斜齿轮)齿面点受力进行分解，如图6所示，其中Fa为轴向力，Fr为径向力。基于输入参数和齿轮几何参数，可推导得到啮合点所受法向力Fni与斜齿轮对所受法向力总和Fn满足如下关系：

(12)

(13)

式中：rb1为主动轮基圆半径；M为输入扭矩，Pw为输入功率。

图6 单侧人字齿轮(斜齿轮)齿面点受力分解

由于重合度的影响，人字齿轮的实际啮合状态为多齿对交替啮合，故应根据接触线分布情况确定载荷分配比γ，进而求得单齿所受法向力。单齿所受法向力Fni与单侧人字齿轮(斜齿轮)所受总法向力Fn的关系如下：

Fni=γFn

(14)

载荷分配比即为某一时刻下某一齿对所受法向力与该时刻单侧人字齿轮(斜齿轮)所受总法向力的比值，其大小等于该齿对啮合产生的时变接触线长度与此时接触线总长的比值，即

γ=li/L

(15)

(5)滑滚比

在热弹流的数值计算过程中，齿面滑滚比起到重要的作用，其大小决定齿面滑动是否明显。基于式(11)对啮合点切向速度的计算，可推导得到滑滚比为

s=|>U1-U2|/Ue

(16)

(6)齿面接触参数变化规律

按照上述人字齿轮基本结构参数、基本工况及公式推导，通过计算可得到齿面接触参数变化规律，如图7所示，图中圆圈标注位置为对应啮合点处的接触参数具体数值。

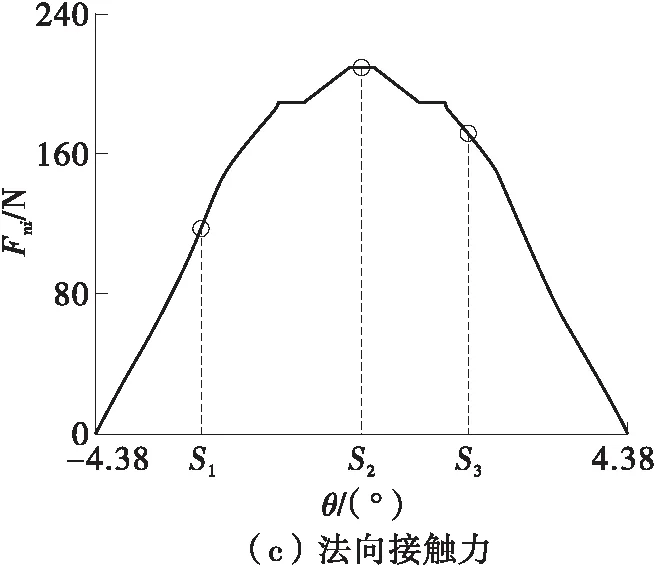
图7 接触参数的变化

2 热弹流润滑理论及数值求解

人字齿轮热弹流润滑分析的本质是基于齿面啮合点接触分析的计算结果，按照一定的计算方法和流程对Reynolds方程等润滑所需偏微分方程联立求解，最终得到啮合点处油膜特征分布的分析计算过程。

2.1 理论方程

(1)膜厚方程

包含表面弹性变形的点接触膜厚方程为

(17)

式中，h0为中心膜厚，E*为当量弹性模量。

(2)Reynolds方程

基于Reynolds方程在热弹流计算时的基本假设，选用的广义二维Reynolds方程为[15]

(18)

式中，p、h分别为油膜的压力和厚度，ρ、η分别为润滑剂的密度和黏度。

Reynolds方程求解时的边界条件为

(19)

(3)能量方程及热界面方程

基于能量方程和热界面方程可求得油膜温度场。能量方程如下：

(20)

式中，cp为定压比热容，k为润滑剂热导率，T为油膜温度，u和v分别为油膜在x、y方向的速度。

能量方程需在已知润滑剂与固体接触界面条件下进行求解，热界面方程可表述为

(21)

式中，T0为初始环境温度，ρ1和ρ2、c1和c2、k1和k2、u1和u2分别为上、下表面齿轮材料的密度、比热容、热导率和切向速度。

(4)载荷平衡方程

点接触热弹流问题需在给定载荷条件下进行求解，并且所求油膜压力分布应与外载荷w相平衡。对于点接触问题，其载荷平衡方程为

(22)

(5)润滑剂特性方程

润滑剂受温度和压力的影响而呈现出的粘压温特性会对热弹流数值计算结果产生影响，本文采用Roelands方程[16]来表征润滑剂的粘压温特性：

(23)

式中：η0为标准大气压下温度为T0时的润滑剂黏度；z可由粘压系数确定，本文取0.68；s0=β(T0-138)/(lnη0+9.67)，β为粘温系数，本文取s0=1.1。

则润滑油密度在温度和压力影响下所呈现的数值变化规律为

(24)

式中，ρ0为标准大气压下温度为T0的润滑油密度，A=0.6×10-9m2/N，B=1.7×10-9m2/N，D=-0.000 65 K-1。

(6)运动方程

能量方程求解的前提是在已知压力分布和油膜厚度的条件下求得油膜速度场的分布。对运动方程积分即可求得油膜在x、y方向的流速，即

(25)

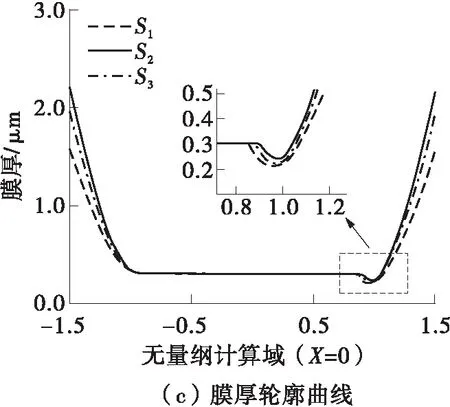
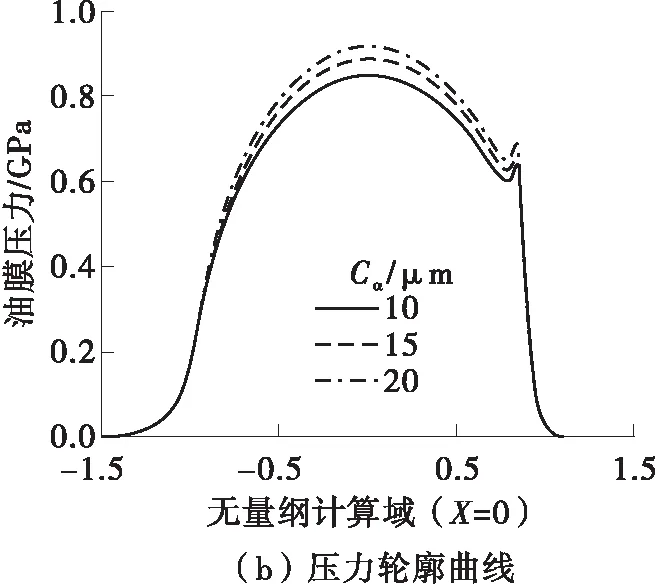
在计算前需对求解所需的理论方程进行必要的无量纲化和离散化处理。本文所用到无量纲变量如下：X=x/a，Y=y/a，-1.5

2.2 程序验证结果

在计算啮合点处热弹流数值之前，需根据已发表文献中的实验数据对本文TEHL程序计算结果的准确性进行验证。为了尽可能贴近喷油工况下的真实齿轮润滑状态，本文引用文献[17]中油滴大小对润滑状态影响这组实验。该组实验对比了不同初始油滴大小对油膜厚度的影响，当液体直径增大到一定值时，油膜厚度的变化不明显，球盘整体处于充分的全膜润滑状态，与本文理想的齿轮实际润滑状态相符。根据文献[17]中实验情况设定相应的润滑剂参数、钢球物性参数和工况参数，计算结果如图8所示。从图8(b)所示的x=0.25、y=0.25刻度线交接处提取中心油膜厚度数值为1.532 7 μm。根据误差计算方法确定计算结果相对误差，即(理论计算中心膜厚-标注点处中心膜厚)/理论计算中心膜厚。文献[17]研究结果表明，当油滴初始直径为100 μm以上时，球盘处于充分全膜润滑状态，油滴通过接触区中心时的中心油膜厚度大约为1 400 nm。相较于TEHL程序计算结果的1 532.7 nm，相对误差为8.66%。在两者结果的对比中需考虑到一些实际因素，基于光干涉法的测量仪器受测量精度(即分辨率)的影响，在膜厚的垂直或水平方向上会产生测量误差。此外，利用不同的方法对Reynolds求解会导致最终油膜分布在数值上有略微的差异。综合上述因素，可认为本文程序的计算结果是可靠的。

图8 理论计算结果

2.3 数值计算结果

在润滑剂的黏度、密度、比热容、热导率分别为0.03 Pa·s、956 kg/m3、2 kJ/(kg·K)、0.14 W/(m·K)，齿轮的密度、比热容、热导率分别为7 860 kg/m3、470 J/(kg·K)、46 W/(m·K)，环境温度为303 K的情况下，对啮合点S1、S2、S3进行热弹流数值求解。从计算结果中提取油膜特征分布二维轮廓曲线和特征参数进行比较，结果如图9、表1所示。在单齿啮入啮出过程中，最大油膜压力受到法向接触力的影响先增后减，最小油膜厚度变化趋势则与之相反。最高油膜温升受法向接触力和滑滚比的影响呈现出与最小油膜厚度相同的变化趋势，齿面节点附近温升较低，啮入、啮出侧温升较高。

图9 啮合点处油膜的二维轮廓曲线

表1 啮合点处油膜的特征参数

2.4 输入转矩和主动轮转速的影响

以啮合点S1为例，设定两组实例对比分析不同输入扭矩和主动轮转速对油膜特征分布的影响，不同实例条件的工况条件设定参数如表2所示，计算结果如图10、11所示。从图中可以看出：随着主动轮转速的上升，油膜厚度增大，主、从动轮齿面间剪切作用的增强导致油膜温升轮廓曲线峰值的上升；油膜压力在数值上变化不大，仅在二次压力峰的位置出现一定程度的偏移；随着输入扭矩的增大，齿面间法向接触力增大，油膜受到的挤压作用增强，油膜压力和温升轮廓曲线峰值都有所上升。从图11(c)的局部放大图可以看出，油膜颈缩位置的峰谷随着输入扭矩的增加而下降。

表2 两组实例的工况参数

图10 实例1中啮合点S1处油膜的二维轮廓曲线

图11 实例2中啮合点S1处油膜的二维轮廓曲线

2.5 鼓形修形量的影响

以啮合点S1为例，在人字齿轮和润滑剂参数同前的基础上，分析鼓形修形量Cα分别为10、15、20 μm时对油膜特征分布的影响，计算结果如图12所示。从图中可知：随着修形量的增加，y方向的当量曲率半径减小，即齿面接触区的接触椭圆面积减小，导致油膜压力上升，但油膜厚度(无量纲计算域X=0处)的变化趋势微弱。在滑滚比和卷吸速度数值变化微弱的前提下，油膜压力的上升势必引起油膜温升曲线的升高[5,18]。因此在实际工程应用中，应根据实际适当地控制修形量，避免啮合点处局部压力、温升的升高并保证良好的润滑状态。

图12 不同修形量对油膜分布的影响

3 齿面摩擦特性分析

弹流润滑中的摩擦力是指润滑油膜于轮齿齿面啮合点运动切向方向产生的切应力，该力由滑动摩擦及滚动摩擦组成。通常情况下，忽略滚动摩擦的微观影响并以滑动摩擦代指油膜所受切应力。滑动摩擦在数值上应等于润滑油膜本体所受的切应力之和。然而，油膜在极短的啮合接触时间内承受较大的剪应变率而导致几百摄氏度的局部温升。在油膜所受的高压力、高剪应变率和局部高温升等条件影响下，润滑油流体往往失去黏性流体特征，表现出非牛顿流体的特性[17]。相较于牛顿模型，Ree-Eyring模型计算非牛顿特性流体所受剪应力的结果更加准确，故本文采用该模型来计算油膜所受到的切应力。

啮合点接触区内油膜所受总摩擦力为[19]

(26)

(27)

(28)

(29)

基于前面对啮合点S1、S2、S3在工况1下的热弹流数值计算结果和式(26)，计算得到啮合点S1、S2、S3处的摩擦系数分别为0.030 9、0.001 0和0.015 2，整体变化趋势与图7(d)滑滚比分布相对应，节点处几近处于纯滚动状态，故摩擦系数接近于0。

4 结论

(1)齿面接触参数的变化规律和啮合点S1、S2、S3处的热弹流数值计算结果表明，油膜压力曲线峰值(最大油膜压力)主要受啮合点法向接触力的影响，先增大后减小，最小油膜厚度变化趋势与其相反。由于齿面啮入、啮出侧滑滚比较大，故油膜温升曲线峰值(最高油膜温升)在齿面两侧数值较大。齿面节点处几近处于纯滚动状态，齿面剪切作用微弱，故温升峰值较低。

(2)随着主动轮输入转速的升高，油膜温升和厚度均有所增大，但油膜压力受转速的影响微弱，变化趋势不明显。当输入扭矩增大时，油膜压力、温升轮廓曲线的峰值明显上升，油膜厚度轮廓曲线(无量纲计算域X=0处)的变化趋势不明显，但颈缩位置的峰谷有所下降。

(3)虽然鼓形修形可以优化齿面受载状态，但修形量会对油膜的特征分布造成一定程度的影响。计算结果表明，随着修形量的增加，油膜压力和温升各自呈现出一定程度的上升趋势，故应在确保润滑不失效的前提下选择合适的修形量。

(4)齿面时变摩擦系数的计算结果表明，从齿面啮入侧至啮出侧，摩擦系数先降后升，即齿面节点附近摩擦系数接近于0，齿轮啮合时几近处于纯滚动状态。啮入、啮出侧齿面点的摩擦系数较大，故齿面、油膜温升较高，与热弹流数值计算结果所表征的变化规律相吻合。在齿面润滑冷却时，应着重关注啮入、啮出侧啮合点，避免齿面胶合等失效现象的发生。