基于计算机视觉的相机标定方法

景国峰

(山东正元数字城市建设有限公司, 山东 烟台 264670)

0 引言

由于相机在制造中受工艺、安装水平等内部因素影响,以及在使用过程中受温度、湿度、压强等外在因素影响,使得相机在成像过程中并不是理想的针孔成像模型。这使得相机传感器的畸变参数,随着设备不断使用及数据采集环境的不断变化,其数值也在随之变化,从而降低了影像空中三角测量的稳定性[1]。因此,在一定的周期内,对传感器畸变参数校正成为实际所需。目前,相机标定原理较为完善成熟,且相机标定是完成影像测量、重建过程中必不可少的一步。针对本文的研究内容,为了提高影像空三的精度与可靠性,对采集影像数据的相机进行标定。

1 相机标定

由于受内在和外在因素影响,相机中不可避免存在一定的内部误差和畸变影响,其中内部误差在摄影测量中又称为内方位元素,为了确定这些误差参数,需要对相机标定[2]。

相机在采集现实世界的信息成像时,以针孔模型作为数学模型,将现实空间中的三维实体映射到相机中的二维平面中。针孔模型以透视变换原理为基础,以局部摄影坐标系作为过渡坐标系,首先将现实世界中的三维实体转换到摄影坐标系中,然后再转换到相机的图像坐标系中,通过两次坐标系的旋转变换,按照中心投影原理将三维空间中的点一一对应到二维图像中[3]。

把现实世界中点参考的坐标系称为世界坐标系,则该坐标系与摄影坐标系之间的转换关系如下所示:

(1)

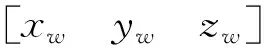
通过式(1)得到局部摄影坐标系下的三维点,根据摄影测量学中的共线方程,建立三维点与二维图像之间的关系如下所示:

(2)

(3)

以上是考虑到相机严格遵照针孔模型原理成像,但是在实际使用中相机受各种因素的综合影响,使得在成像时并不是理想的针孔模型。

在摄影测量学中，从摄影中心往图像做垂线,与图像的交点称为像主点,理论上认为像主点在图像中心点o处。但是,由于相机内部误差的原因,实际的交点位置o1与图像中心存在一定误差。如式(4)、式(5)所示,把这种误差作为相机的内方位元素(x0,y0)。

x0=x01-x0

(4)

y0=y01-y0

(5)

其中,(x0,y0)与(x01,y01)是以图像左上角为原点的像素坐标系中的点坐标;(x0,y0)为图像中心点坐标,(x01,y01)为实际相机标定出的像主点坐标。

相机在实际成像与理想成像在图像坐标系上存在一定畸变。空间点P(x,y,z)在理想情况下成像在图像的pu(xu,yu)位置处,但是由于畸变原因使得实际成像位置却在pd(xd,yd)处[4]。相机的畸变可分为径向畸变与切向畸变,其切向畸变比径向畸变小得多,在实际中一般只考虑径向畸变对影像成像的影响。径向畸变差通常用如下公式表示[5]：

Δr=k0r+k1r3+k2r5+k3r7+k4r9+…

(6)

式中,Δr为径向畸变差;r为像片的像点到像主点距离;k0,k1,k2,…为畸变系数。

畸变差在x,y方向上的改正数ΔxΔy表示为：

(7)

(8)

2 基于计算机视觉的相机标定法

综上分析,相机标定的目的是获得相机的内参元素与畸变参数,是三维重建不可缺少的一步。

在相机标定中参照针孔模型通常把像主点在图像中的位置以及相机焦距组成的矩阵称为内参矩阵,图像像素坐标与标定板坐标之间的关系如下[6]:

q=MQ

(9)

其中

(10)

式中q是以图像左上角为坐标原点的像素坐标;矩阵M中fx、fy为相机x轴与y轴方向的焦距;s表示成像平面x轴与y轴方向的不正交性,一般s为0;

对于棋盘格不同位置处的点到相机的成像过程可用下式表示:

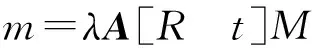
(11)

(12)

在相机标定中假定标定板在世界坐标系Z=0的平面上,则式(12)可进一步简化为[7]:

(13)

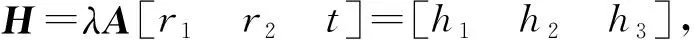
(14)

式中旋转向量在构造中是相互正交的,将缩放因子提到外面,则r1与r2相互正交，如下所示：

(15)

根据两向量正交的含义,则有以下两个基本的约束条件如下:

(16)

(17)

(18)

实际上矩阵B有通用形式的封闭解如下所示：

(19)

(20)

(21)

如果有K个棋盘图像,累积列出这些方程,如下所示：

Vb=0

(22)

式中V是一个2×K×6的矩阵,在矩阵B通用形式的封闭解中得到[8]:

(23)

对于旋转与平移通过下式得到:

(24)

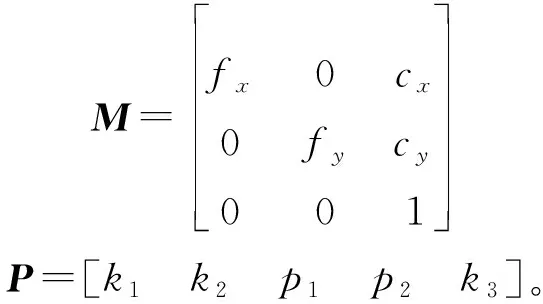
结合针孔模型,利用畸变参数对(xd,yd)畸变点进行纠正得到正确点(xp,yp),如下所示[9]:

(25)

3 试验过程及方法

根据相机标定原理,以计算机视觉中的标定方法为基础,对相机传感器设备进行参数标定计算。按照如下算法过程进行标定:

(1)从不同角度拍摄获取标定图片;

(2)对每一张标定图片,提取角点信息,并进一步提取亚像素角点信息;

(3)初始化参数求解,获得相机内插的初始值,将畸变参数设置为0,最小二乘总体迭代求解,获得相机标定结果。

(4)对最后的标定结果精度分析,利用畸变参数进行矫正。

3.1 标定结果

利用自制标定板,在相机相对于标定板的不同角度、不同距离处拍摄系列图像,如图1所示。

图1 采集标定图像

在标定程序中计算相机的畸变参数P与内参元素M,并对空间三维点反算投影点,计算标定投影误差v。

P=(0.987 627-40.872 50.004 510.011 72816.122 5)

其中投影误差V为0.170 8个像素。

利用畸变参数P进行标定图像的畸变纠正,如图2、图4所示,为原始未畸变影像,利用本文算出的畸变参数进行畸变纠正处理,结果如图3、图5所示。

图2 原始标定图像 图3 畸变纠正后图像

图4 原始标定图像 图5 原始标定图像

相机标定的内参元素,在影像的定向中提供像主点的精确位置,可提高影像定向精度。

3.2 精度对比分析

为了验证本文计算畸变参数的可靠性,以相机传感器获取的初始影像为原始数据,同时不加入畸变参数,以PhotoScan软件进行空三计算[10],其计算结果如图6所示,可看出影像前方交会出的稀疏点云存在错乱,说明其计算的影像外方位元素存在问题。

将上述3.1中计算的畸变参数应用到其采集的影像空三中,同时加入畸变参数,同样以PhotoScan软件进行空三计算,其计算结果如图7所示,可看出影像前方交会出的稀疏点云稳定一致,说明加入畸变参数后极大提高了空三的精度。

图6 未加入畸变参数结果 图7 加入畸变参数结果

4 结束语

本文以解决传感器畸变参数的准确性为出发点,介绍相机成像原理及相机标定的方法,对相机标定进行实验分析,以达到准确标定相机参数的目的,并将计算的畸变参数应用于数据处理。通过对比分析,其计算的畸变参数可提高空三精度。