t-分布扰动策略和变异策略的花授粉算法
2021-02-05宁杰琼
宁杰琼,何 庆
(贵州大学 大数据与信息工程学院,贵阳 550025) (贵州大学 贵州省公共大数据重点实验室,贵阳 550025)
1 引 言
近年来许多学者越来越重视元启发式群智能算法,通过不断地研究提出了一系列的群智能优化算法,常用的包括粒子群优化算法(PSO)[1]、萤火虫算法(FA)[2]、蝙蝠算法(BA)[3]、布谷鸟算法(CS)[4]等.花授粉算法(Flower pollination algorithm,FPA)是英国剑桥大学学者Yang于2012年提出的一种新型元启发式群智能优化算法[5].该算法模拟了显花植物的异花授粉和自花授粉这两个过程,与算法中的全局搜索机制和局部搜索机制相对应.由于该算法超参数少,结构简单,易于实现,从而受到学者的广泛关注.目前花授粉算法已经成功应用于多目标优化、函数优化等问题中.但是,与其他群智能算法类似,FPA算法存在易陷入局部最优、迭代后期收敛速度慢、寻优精度差等缺点.
为了解决这些问题,使FPA算法的性能进一步提高,近年来国内外出现了很多对此算法的改进.邵良杉等[6]提出了一种基于天牛须搜索的花授粉算法,将天牛须搜索引入到全局搜索阶段,在局部搜索阶段加入变异策略使算法能够跳出局部最优,结果表明算法在低维和高维下收敛速度和精度都得到了提高.陈西成等[7]将小生境策略和混沌优化策略应用到花授粉算法中,结果表明在两种策略的结合下,避免了算法早熟收敛,提升了全局寻优能力,同时算法的搜索精度也得到了显著提高.肖辉辉等[8]在迭代前期只将高斯变异引入到花授粉算法的全局寻优部分,迭代后期在引入高斯变异的同时,将Powell搜索法引入到局部搜索过程中,结果表明GMPFPA算法相比于FPA算法,收敛精度有了明显提高.刘景森等人[9]将模拟退火机制融入花授粉算法中,并且将全局步长和局部繁衍概率结合迭代次数来进行改进,结果表明算法的寻优精度和收敛速度均有较大提升.Shambour[10]等人在全局寻优部分利用进化过程中随机选取的两个解信息,将算法的探测部分调整到特定的搜索区域,结果表明所提出的mgFPA算法与FPA算法相比,解的质量得到进一步地提高.Nabil[11]将基本花授粉算法与克隆选择算法(CSA)融合,实验结果表明该算法的寻优精度和收敛速度有了一定程度的提高.
以上文献对基本花授粉算法都有一定程度的改进,大部分算法相较于FPA算法,收敛速度明显加快,解的质量得到一定程度的提高,但在寻优精度、收敛性能等方面还有很大的提升空间,而且Shambour[10]等人和Nabil[11]只是在低维情况下对改进花授粉算法的性能进行了测试,没有在高维情况下对算法的性能进行测试.由于大部分的群智能算法存在容易陷入局部最优这一缺点,有学者加入了变异因子进行扰动,例如,贺智明等人将柯西变异引入到传统花授粉算法中[12],沈鑫等人在差分进化算法的变异操作中加入柯西扰动[13],王越等人将变异算子加入二进制粒子群优化算法[14],而t-分布扰动算子很少被使用到.因此,本文提出t-分布扰动策略和变异策略的花授粉算法(tMFPA).该算法将t-分布扰动策略和差分变异策略分别引入到全局授粉过程和局部授粉过程,最终选取7个基本测试函数进行实验,验证了tMFPA算法在收敛能力和搜索能力上的有效性和优越性.
2 相关工作
2.1 花授粉算法
花授粉算法模拟了自然界中显花植物的花朵授粉过程.为了简化问题,使算法更加高效,同时考虑到优化问题仅有一个解,Yang假设每株显花植物都只能孕育出一朵花,并且每朵花只能产生一个花粉配子.根据文献[5]的描述,花朵授粉过程可以总结为以下4条规律:
a)生物异花授粉被视为全局授粉过程,花粉载体携带花粉执行Levy飞行.
b)非生物自花授粉被视为局部授粉过程.
c)繁衍概率即为花的恒常性,繁衍概率的取值大小与两朵花的相似性成正比.
d)利用转换概率p∈[0,1]来控制局部授粉和全局授粉的转换.
通过以上规则,建立如下的数学模型:
定义1.在全局授粉过程中,花粉的位置更新公式为:
(1)

(2)
其中,Γ(λ)是标准伽马函数;λ=1.5.
定义2.局部授粉阶段的位置更新公式如下:
(3)
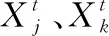
定义3.通过转换概率p∈[0,1]取值来控制全局授粉和局部授粉之间的转换,经过大量仿真实验表明,当p=0.8时,算法可以得到最好的寻优性能.
2.2 差分变异
差分进化算法(Differential evolution algorithm,DE)是由Storn等人提出的一种启发式算法[15],该算法包括3种算子:差分变异算子、交叉算子和选择算子.在这3种算子中,差分变异算子有着核心地位,起着至关重要的作用.差分进化变异策略最基本的变异策略如下:
(4)
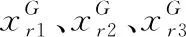
差分进化变异策略还有其他变种[16],如:
(5)
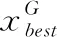
Zheng等[17]在研究了差分进化算法后,提出了一种新的差分进化策略:
(6)
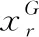
3 t-分布扰动策略和变异策略的花授粉算法
3.1 混沌映射初始化花朵个体位置
由于传统花授粉算法采用随机方式对花朵个体的位置进行初始化,这就可能导致花朵个体的初始位置分布不均匀.混沌具有随机性、对初值敏感等特点,可以在一定范围内按照自己的规律遍历所有状态而不重复[18],因此本文利用混沌映射来初始化花朵个体的位置,使花朵个体的初始位置分布地更加均匀.针对n个花朵个体(d维空间),本文采用混沌映射初始化种群的步骤如下:
a)首先随机产生一个在[0,1]区间内的d维向量c1(第一个花粉个体).
b)利用logistic映射[19]迭代产生其余的n-1个向量,logistic映射公式如下:
ci+1=μci(1-ci)
(7)
其中,μ为控制参数,当μ=4时,logistic映射分布最均匀,ci为花朵个体经过混沌映射后的位置,i=1,2,3,…,n-1.
c)将混沌映射后的值再映射到解的搜索空间中,公式如下:
xi=L+ci(U-L)
(8)
其中,L和U分别是搜索空间的上下限,xi是花朵个体在搜索空间中的初始位置.
3.2 基于t-分布扰动策略的全局搜索
在基本花授粉算法中,全局搜索是在当前最优的花朵个体的基础上,使用莱维飞行函数来反映昆虫等授粉者的飞行轨迹,更新当前花朵个体的位置生成新解.由于莱维飞行具有步长长短相间和跳跃方向多变的特点,算法可以在相应范围对花朵进行全局搜索,但也可能会因跳跃太大导致最优花朵个体信息的丢失.而且每一代花朵位置的更新都是通过当前一代的位置和最优位置利用莱维飞行机制更新,不能有效地拓展搜索空间.因此,tMFPA在保留莱维飞行特征的同时,将种群中其他个体的信息引入到全局搜索更新机制中,通过在个体之间交换信息来调整位置更新机制,增强了搜索空间的多样性.为了使其他花朵个体能够尽可能地被遍历到,引入t-分布扰动算子对随机花朵个体进行扰动.改进后的全局搜索位置更新公式为:
(9)
其中,m∈[0,1],步长γ的表达式如下:
γ=0.01+0.49(t/N_iter)
(10)
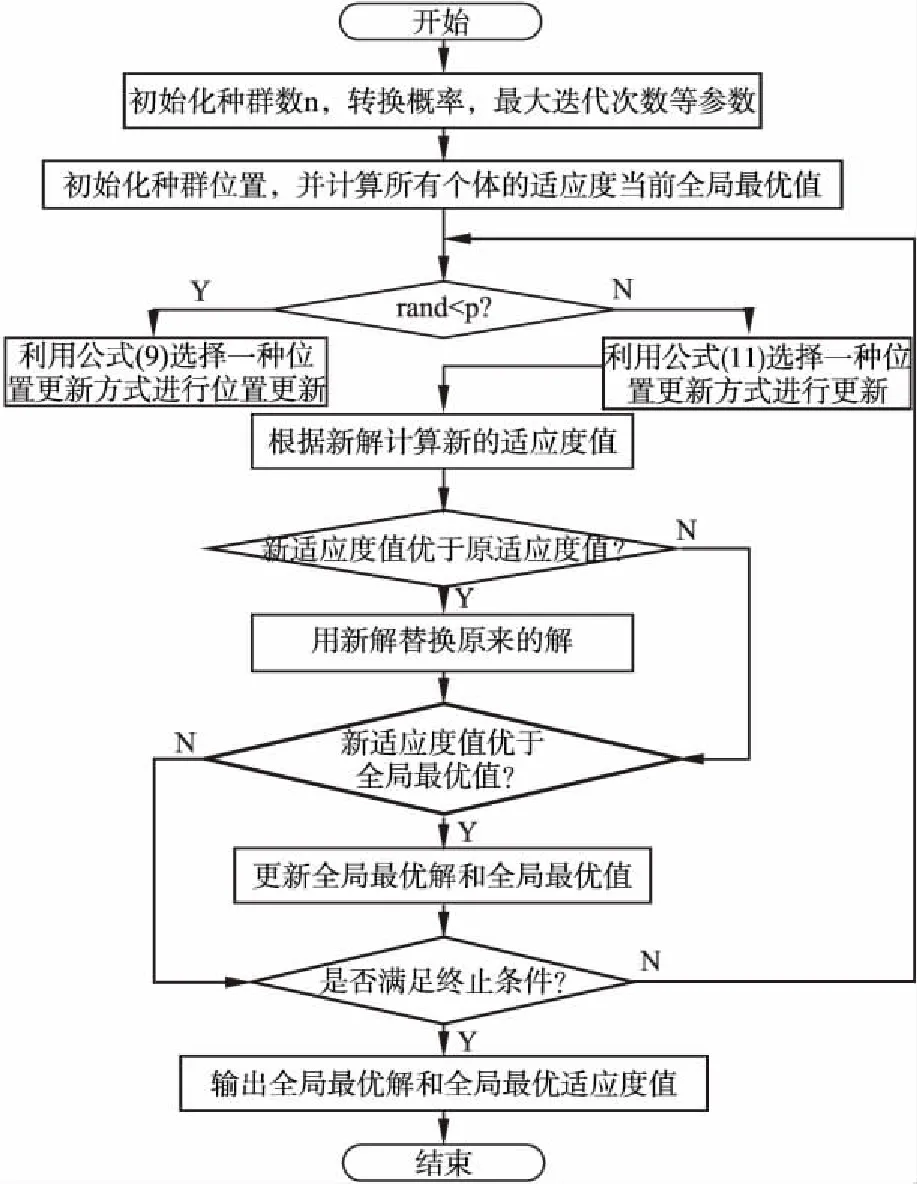
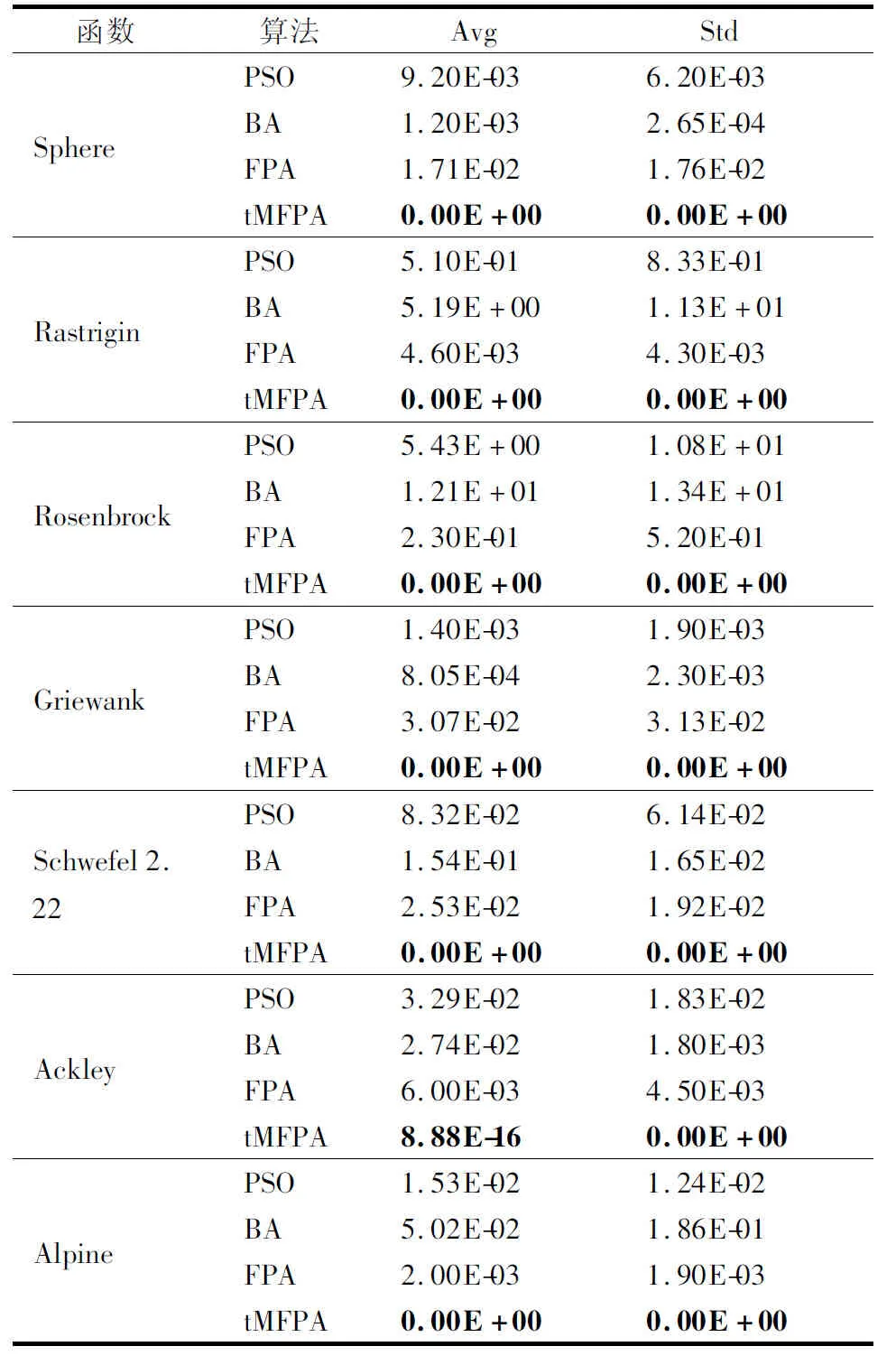
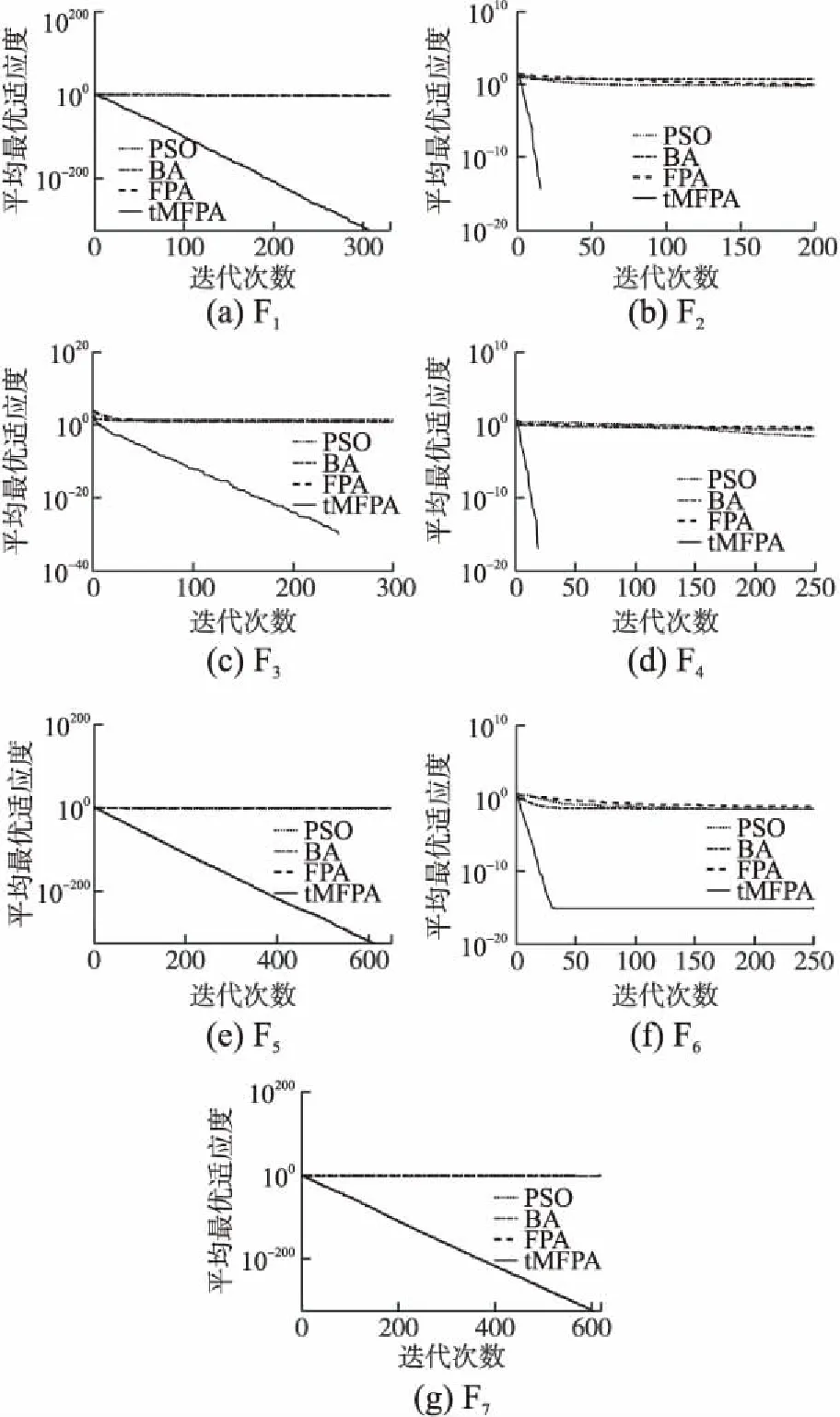
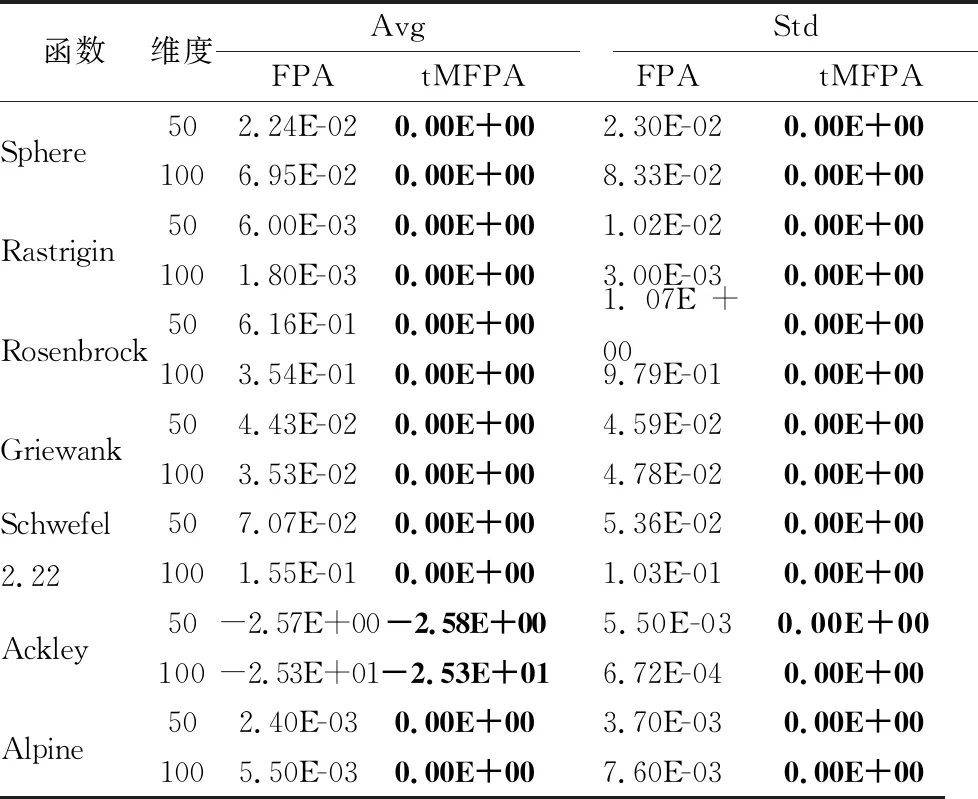
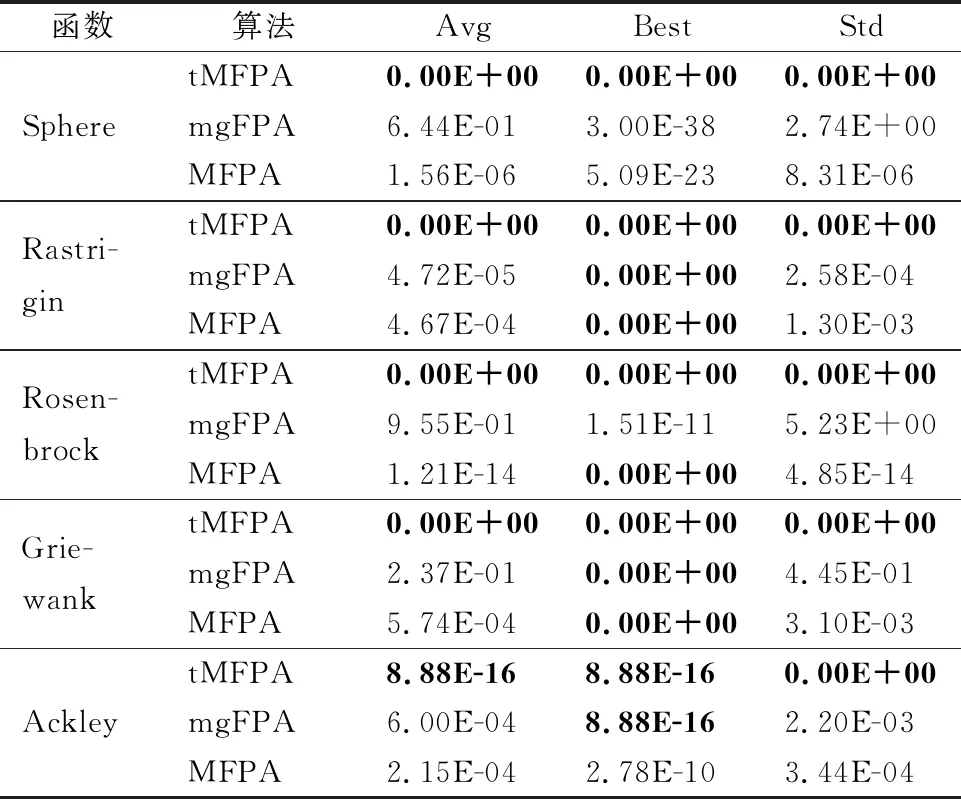
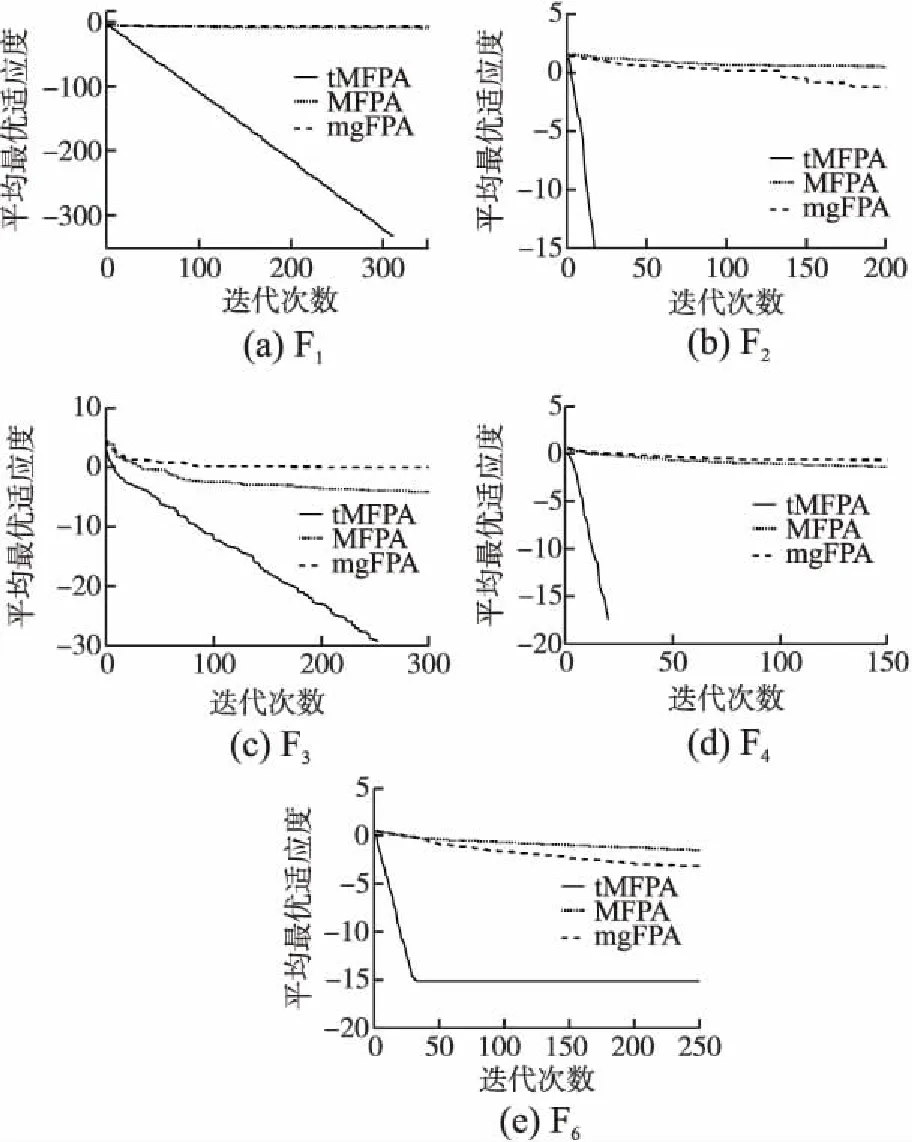
公式(9)对随机花朵个体进行t-分布扰动,t-分布的自由度随着迭代次数的变化而变化.随着自由度参数t值的增长,数值分布状态逐渐由Cauchy分布趋近于Gaussian分布.算法迭代前期,t-分布表现出的特征与Cauchy分布特征一致,帮助开采新的搜索空间,提高算法的全局搜索能力;在中后期时,t-分布表现出的特征与Gaussian分布特征一致,有助于算法在当前解邻域范围内进行搜索.在改进的位置更新公式中,将全局搜索策略分为两部分,在每次迭代时评估rand和m的关系以确定使用哪种方法.当rand 相对于单个差分向量的策略,具有两个差分向量的变异策略可以提高种群的多样性,并且仅使用单个差分向量策略仍有可能使算法陷入局部最优,而算法可以得到全局最优的关键是算法能否跳出局部最优.因此将原始差分变异策略根据式(5)和式(6)进行改进,将改进后的差分变异策略引入到局部搜索,在全局最优解的基础上,保持了差分向量确定性与随机性的平衡,提高了种群的多样性,在此基础上,将小概率变异策略引入局部搜索,通过判断rand和q之间的关系来决定使用哪种更新方式,最终通过两种策略的结合提高算法跳出局部最优的能力.改进后的局部搜索位置更新公式为: (11) 针对花授粉算法的局限性,本文提出了t-分布扰动策略和变异策略的花授粉算法(tMFPA),将t-分布扰动策略和差分变异策略分别引入到全局授粉过程和局部授粉过程中,tMFPA算法的具体实施步骤如下: a)初始化. 初始化算法的参数:种群数n,转换概率p,最大迭代次数N_iter等参数.利用混沌映射初始化种群的位置,计算每个花朵个体的适应度值,并求解出当前的全局最优值. b)个体位置更新、全局最优值更新. 若rand c)判断算法是否结束. 如果算法满足结束条件就输出最优花朵个体位置和全局最优目标函数值;如果不满足,转到步骤b),直到满足结束条件. tMFPA算法的具体流程图见图1. 图1 tMFPA算法流程Fig.1 Schematic diagram of tMFPA 假设优化的目标函数为f(x),解空间的维数为d,根据FPA算法的步骤,FPA的时间复杂度为O(d+f(d)).根据tMFPA算法步骤,假设种群规模为n,利用混沌映射产生花朵个体初始位置的时间复杂度为O(nd),根据初始位置生成适应度值的时间为f(d),基于t-分布扰动策略的全局搜索:Levy飞行生成步长的时间为ξ2,产生t-分布随机数的时间为ξ3,根据当前位置产生下一代的时间为ξ4;基于变异策略的局部搜索:产生随机数的时间为ξ5,计算随机变异算子的时间为ξ6,根据当前位置产生下一代的时间为ξ7.由新位置生成新适应度值的时间为f(d). 全局寻优过程的时间复杂度为: (12) 局部寻优过程的时间复杂度为: (13) 假设所得到的新适应度值与当前适应度值进行比较的时间为μ2,经过比较,如果新适应度值更好,需要替换当前适应度所需时间为μ3,所得到的新适应度值与当前最优值进行比较的时间为μ4,如果需要替换当前最优值所需时间为μ5,则算法总的时间复杂度为: (14) 为了验证本文所提出的tMFPA算法的有效性,以求最小值为例,用7个经典性能测试函数对基本花授粉算法、粒子群算法、蝙蝠算法和本文改进的算法进行MATLAB实验仿真对比.表1列出了7个函数的空间维度、搜索范围、最优解.为了降低算法随机性对实验性能的影响,以30次独立实验的平均值作为评估算法寻优性能和收敛性能的最终结果.实验时各种算法的参数为:FPA算法参数:转换概率p=0.8,λ=1.5;PSO算法参数:c1=c2=2,w=0.9,vmax=1;BA参数:A=0.25,r=0.5,alf=0.95;本文改进tMFPA算法参数:转换概率p=0.8,λ=1.5. 表1 测试函数Table 1 Test functions 为了验证本文提出的tMFPA算法的性能,分析算法在低维、高维情况下的寻优能力和收敛速度,同时排除实验结果的偶然性,仿真实验的每种算法独立运行30次,最大迭代次数设为2000次. 4.2.1 低维下的性能测试 通过在7种测试函数上进行仿真实验,比较4种算法的收敛能力和寻优能力.仿真测试中,种群数量统一设置为40,维度设为30.表2给出了4种算法在不同测试函数下的平均值和标准差.同时,为了更直观地了解算法的有效性,对比4种算法的寻优性能,图2给出了它们在不同函数上的收敛曲线对比图,同时为了便于观察,横坐标为普通坐标轴,纵坐标为对数坐标轴. 表2 4种算法的迭代寻优结果Table 2 Iterative optimization results of 4 algorithms 根据表2中的实验数据和图2的迭代曲线,分析如下: 由表2数据可以看出,在规定迭代次数下,tMFPA算法能找到Sphere、Rastrigin、Rosenbrock、Griewank、Schwefel 2.22和Alpine函数的理论最优值,找到的平均值为全局最优值,而FPA、PSO和BA对这些函数寻优的效果都不明显.Ackley函数较复杂,很难找到其理论最优值,从表2的实验数据看出,tMFPA最终收敛到10-16的精度,与其他3种算法相比,提升了14个左右的数量级.从图2(a)-图2(e)和图2(g)可以看出其他3种算法会较早的陷入局部最优,例如,在对Griewank函数寻优时,由图2(d)可以看出,PSO和BA与FPA相比具有一定的优越性,能够逐渐跳出局部最优,但是出现了寻优停滞的现象;在对Alpine函数进行寻优时,其他3种算法在200代左右陷入局部最优之后,一直无法跳出.而从图2(a)-图2(e)和图2(g)可以看出tMFPA算法能够以更快的速度收敛找到全局最优值,其中,对Sphere函数寻优时在300代左右找到了理论最优值;对Rastrigin函数进行寻优时,tMFPA表现出了良好的竞争优势,收敛速度明显加快,并能在30代以内找到理论最优值;对Rosenbrock函数寻优时,tMFPA能够朝向正确的方向以很快的速度收敛到全局最优值,并且在250代左右找到理论最优值;对Griewank函数寻优时,在20代左右找到理论最优值;对Schwefel 2.22函数和Alpine函数寻优时,tMFPA算法即使陷入局部最优值,也能迅速跳出,并在600代左右找到了全局最优值.但是在对Ackley函数寻优时,从图2(f)可以看出,FPA、PSO和BA较早的陷入局部最优,而tMFPA在迭代初期能够迅速跳出局部最优,但是还是在50代左右陷入局部最优值. 图2 4种算法的寻优迭代曲线Fig.2 Optimal iteration curves of four algorithms 从上述分析可以看出,在两种策略的共同作用下,tMFPA算法的寻优精度明显高于FPA、PSO和BA这3种对比算法,而且收敛速度和稳定性更好. 4.2.2 高维下的性能测试 通过在7种测试函数上进行仿真实验,比较tMFPA算法和FPA算法的收敛能力和寻优能力.仿真测试中,维度分别设为50和100.表3给出了2 种算法在不同维度、不同测试函数下的平均值及标准差.根据表3可知,除Ackley函数外,其他函数在高维下仍可以寻优成功,证明tMFPA算法在对高维测试函数进行优化时同样具有良好的效果. 由表3的高维实验数据可以看出,维度从50维变化到100维时,除Ackley函数外,对于其他函数的寻优,tMFPA算法总能找到理论最优值,而且找到的平均值是理论最优值,但是FPA在这7个测试函数中都无法求解到理论最优值,表现出改进算法tMFPA在高维条件下优越的寻优性能. 表3 不同维度下的寻优精度结果Table 3 Optimization accuracy values in different dimensions 从分析中可知,tMFPA算法在高维条件下的寻优精度和收敛速度明显优于FPA算法,这主要是因为在全局搜索过程中加入了t-分布扰动策略,扩大了搜索空间,帮助算法跳出局部最优,加快收敛速度,同时在局部搜索过程中加入了差分变异策略,并引入小概率策略,增强了种群的多样性,使得解的多样性得到提高. 综上,tMFPA算法在30、50和100维条件下,整体上都表现出较好的寻优性能,而且随着维度的增加,tMFPA不受其影响,在高维条件下,也能表现出较好的收敛性能和寻优性能. 4.2.3 本文改进算法与其他文献中改进算法进行比较 为了进一步体现tMFPA算法的优越性,本文利用tMFPA算法和文献[10]的mgFPA算法、文献[11]的MFPA算法对5个测试函数寻优,并对寻优结果进行对比,结果见表4.表4列出了3种算法在5个测试函数下的平均值、最优值和标准差.其中,维度统一设为30,种群规模n=40,最大迭代次数为1000次,转换概率p=0.8,其他改进算法的参数设置与参考文献相同,每种算法独立运行30次,实验数据取小数点后2位.图3为tMFPA算法与其他改进FPA算法的寻优迭代曲线,其中纵坐标为适应度值取以10为底的对数. 表4 3种改进算法的迭代寻优结果对比Table 4 Comparison of iterative optimization results of three improved FPA algorithms 图3 tMFPA与其他改进算法的寻优迭代曲线Fig.3 Optimal iteration curves of tMFPA and other improved FPA 由表4可知,在对选取的5个测试函数寻优时,tMFPA算法与mgFPA、MFPA相比,都有更好的寻优精度.对比mgFPA和MFPA,除函数Ackley外,tMFPA算法在其他函数上找到的平均值、最优值都为理论最优值.mgFPA在函数Rastrigin和Griewank上找到的最优值为理论最优值,但是其找到的平均值与tMFPA相差较大,没有找到理论最优;在函数Ackley上找到的最优值与tMFPA相同,但是找到的平均值比tMFPA算法低12个数量级.MFPA在函数Rastrigin、Rosenbrock和Griewank上找到的最优值为理论最优值,但是找到的平均值都不是理论最优值.由此可证明,改进后的tMFPA算法具有更好的寻优精度. 通过图3(a)-图3(e)可以直观地看出,纵向观察,在100次迭代内,tMFPA算法的收敛曲线始终位于mgFPA算法和MFPA算法收敛曲线的下方,说明在相同的迭代次数下,tMFPA算法具有更高的收敛精度;横向观察,在收敛精度相同的情况下,tMFPA算法具有更快的收敛速度.由图3(a)-图3(d)可以看出,tMFPA算法从迭代开始一直到结束都能快速跳出局部最优,并最终找到了理论最优值,而mgFPA算法和MFPA算法寻优速度缓慢,最终陷入局部最优.由图3(e)可以看出,tMFPA算法在迭代初期能够迅速跳出局部最优,但是还是在50代左右陷入局部最优值,而且从表4可以得到,tMFPA最终收敛到10-16的精度,与其他两种改进算法相比,提升了12个数量级. 针对FPA算法的缺点,本文在传统花授粉算法的基础上进行改进,将t-分布扰动策略、差分变异策略分别引入到全局寻优机制和局部寻优机制中,提出了t-分布扰动策略和变异策略的花授粉算法.全局寻优过程中,在保留莱维飞行特征的同时,将种群中其他个体的信息引入到全局搜索更新机制中;局部寻优过程中,引入具有两个差分向量的变异策略和小概率策略.通过进行tMFPA算法低维情况下性能测试、高维情况下性能测试、3种改进算法对比3项实验,结果证明,本文tMFPA算法相比于其他算法具有更强的竞争优势.3.3 基于变异策略的局部搜索
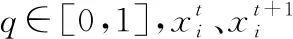
3.4 算法实现
3.5 tMFPA算法复杂度分析
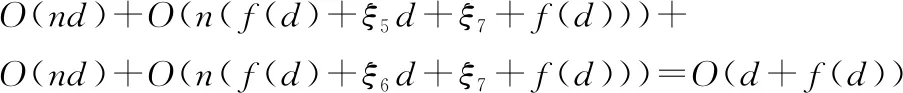
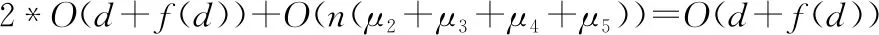
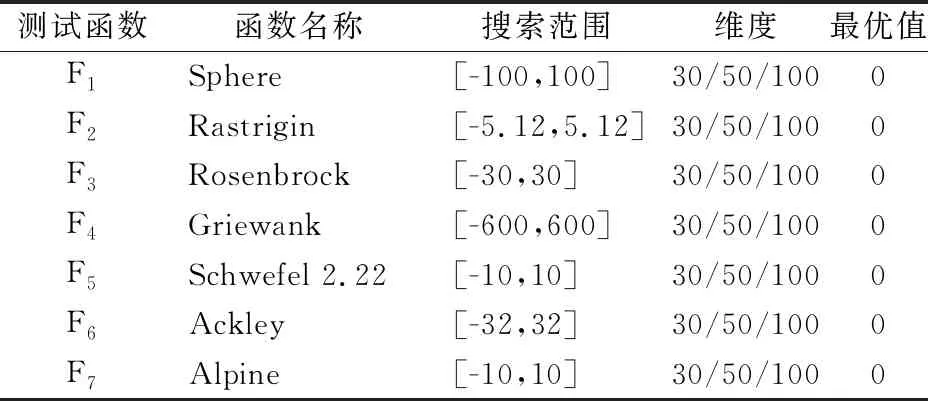
4 实验仿真与结果分析
4.1 实验设计
4.2 实验结果与分析
5 结束语
