引入IVHFS的数学表达式检索结果排序方法

韩 苹，田学东

(河北大学 网络空间安全与计算机学院，河北 保定 071002)

1 引 言

传统面向一维文本的检索方法很难对数学表达式这种特殊的信息表现形式进行检索和处理，且数学表达式检索的查询式和检索结果会因为数学表达式丰富的语法语义变换特性而存在需求偏离的情况，导致检索性能降低.因此，有必要针对以数学表达式为查询关键词的数学表达式检索结果排序.

国内外针对数学表达式检索的研究取得了一定的进展.在公式检索结果排序方面，Mansouri等人[1]为使排序更为准确、有效，引入了一种新的外观符号布局树(Symbol Layout Trees，SLTs)、运算符树(Operator Trees，OPTs)两个分层的公式嵌入模型，提高公式间相似性的精确度.Math-aware[2]是一种能够结合数学公式布局和语义特征的三层公式搜索模型，结合并行索引和相似度评价方法，在公式的检索结果排名中能够提高检索的排序效果和质量.Dallas等人[3]融合数学表达式符号布局树的特征作为关键搜索词，并使用BM25文本排序方法，实现基于数学和文本之间的搜索.DLMF(Digital Library of Mathematical Functions)Search[4]主要是针对数学图书馆而建立的数学表达式检索系统在检索结果排序方面先后改进了TF-IDF[5]算法，从而实现对数学检索内容的检索.

宰新宇等人[6]在对科技文档检索时融入了一种词嵌入语言模型，弥补了单一的公式对文档检索造成绝对性的影响，结合上下文语义特征构建了一种融合公式和语义特征的科技文档检索模型，从而实现检索结果更为有效、合理的排序.孟祥福等人[7]提出一种空间关键字个性化语义查询方法，该方法能够完整显示原有信息的个性化查询，提高个性化查询程度和准确率.黄莺等人[8]利用用户的个性化信息，融合扩展检索技术，优化了检索结果排序，减少用户获取资源的时间.崔晓娟等人[9]在提取数学表达式的检索特征上构建了分层结构索引表，采用TF-IDF对文档向量赋予权值，利用余弦相似度来计算检索向量和文档之间的相似度，最终实现有关数学表达式的科技文档检索结果的有序输出.

由于数学表达式属于多种符号构成的复杂二维模式，如何将其在符号、语法、语义等方面的属性合理融合，获取符合用户需求的数学表达式检索结果，成为一项关键问题.本文将数学表达式检索结果排序问题转化成模糊信息决策问题，利用IVHFS理论在多属性决策上的优势，求得数学表达式间的相似性距离，从而得到排序结果.其中，该理论的优势主要概括为3个方面：

1)保留信息的犹豫性和模糊性，贴合人类描述信息形式，确保了数学表达式属性信息的有效性和完整性；

2)将属性信息映射为多个区间值的评价指标，扩展了决策信息的不定性描述，从而削弱数学表达式属性评价指标的不确定因素，提高描述信息的灵活性，使得检索结果更加合理化；

3)区间的左右端点，分别代表属性指标的最小和最大值，避免评估信息的主观性，很好地解决了不完全信息中的决策问题.

2 相关工作

区间值犹豫模糊集

在多属性决策问题中，为了描述信息中的不确定性，表达人们对事物的刻画，1965年Zadeh[10]提出了模糊集的概念，来描述人们对于事物的评判.2010年Torra[11]提出了犹豫模糊集，拓展了描述隶属度函数方面的局限.2013年陈树伟等人[12]提出了区间值犹豫模糊集理论，进一步完善了隶属度函数的取值范围.因此，引入区间值来增强决策信息的犹豫偏好程度，可以使决策结果更加合理并贴合实际.

定义 1[12，13].设非空集合为X={x1，x2，…，xn}，则关于X的区间值犹豫模糊集为：

(1)

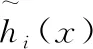
(2)

偏差函数为：

(3)

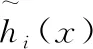
根据得分函数和偏差函数可以比较两个区间值犹豫模糊元素的大小，它们之间的比较法则[12，14]为：

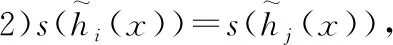
3 数学表达式相似度评价方法

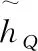
(4)

4 基于IVHFS的数学表达式检索结果排序方法

在对数学表达式属性特征信息描述中，一般的描述方法是将属性评价信息用某一精确的数值来描述.但是，当某一对象的属性评价值有多个时，精确值则无法完全概括，导致部分信息丢失，影响排序效果.因此，采用IVHFS理论对数学表达式进行综合评价，将某一对象属性以多个可能的区间值集合的形式表示出来，可以更好描述评估属性信息，解决数学表达式评价中的不确定性问题，从而判断数学表达式之间的相似度，实现以数学表达式为查询关键字的数学表达式检索结果排序.故将其引入数学表达式检索结果排序问题.本文主要对包含式查询，且主要分为两个部分：确定数学表达式区间值属性以及对IVHFS集合进行相似度评价.

4.1 数学表达式的多属性评价指标

IVHFS对数学表达式进行多属性描述，其优势主要体现在两个方面：1)利用IVHFS的模糊性和犹豫特性，贴近人类语言表述形式，诸如“好”，“坏”等态度词汇，能更加灵活地描述属性信息；2)利用区间值可以减少重复出现的子式以及符号属性的描述，从而形成基于数学表达式的综合评价属性的IVHFS集合.数学表达式属性评价指标如图1所示.

图1中评价指标的设计主要围绕查询式、运算符和运算数3方面属性.其中，属性提取规则是根据FDS(Formula Description Structure)[15-17]做了改进，可简单描述为：提取查询子式、运算符和运算数中的FDS属性特征.

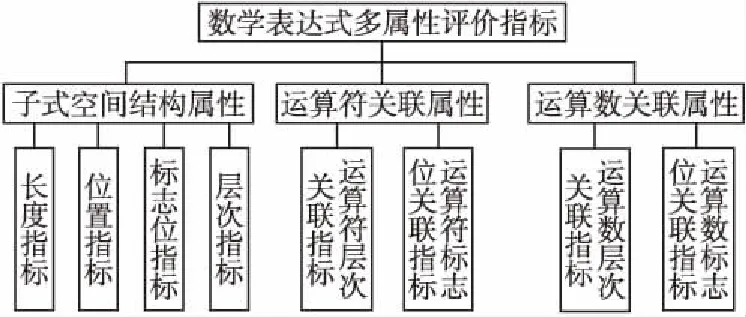
图1 数学表达式属性评价指标结构图Fig.1 Structure diagram of formula attribute evaluation index

4.1.1 子式空间结构属性

将Q作为一个整体，将其看成单独的“运算符”或“运算数”，利用改进的FDS方法提取子式属性特征.

1)长度指标

定义 4.子式长度指标隶属函数为：

(5)

lenQ、lenRQt分别为Q和RQt的符号总数；Q在RQt中所占比例越大，相似度越高，两个公式越相似.

2)位置指标

Q在RQt中的位置越靠前，Q对于RQt越重要，公式的相似度越高.当RQt中有多个Q时，pos的指标函数可以用区间值的形式来表示，取位于RQt中靠前的Q所在位置函数值为区间值的左端点，RQt中最后一个Q的位置函数值为区间的右端点.

定义 5.位置指标隶属函数可以表示为：

(6)

其中，e-β(pos-1)是位置属性权重函数，pos(1，2，3，…)表示解析公式Q在RQt中的位置，β是位置属性权重系数，该区间越接近[1，1]，RQt和Q的相似度越高.

所以，相似度大小为：sim(Q1，RQ1)>sim(Q1，RQ2)

3)标志位指标

数学表达式特殊的二维结构关系可以用标志位表示其所

图2 公式标志位示意图Fig.2 Schematic diagram of formula flag

在空间位置关系情况，图2为标志位示意图，0-8数字依次代表8种位置状态关系.其中，每个标志位所在的重要程度不同，标志位权重越高，说明公式在该标志位的可能性越大，公式间相似度越高.

定义 6.标志位隶属函数为：

(7)

4)层次指标

RQt中Q层次越接近主基线位置，相似度越高，排序越靠前.

定义 7.层次隶属函数为：

(8)

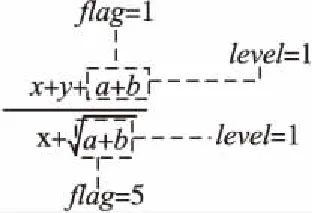
图3 RQ3改进的FDS示意图Fig.3 Improved FDS diagram of RQ3

表1 RQ3的子式空间结构属性区间值Table 1 Interval values of subspace structure attribute of RQ3

4.1.2 符号关联评价指标

符号关联度评价指标反映了符号在数据集中出现的频度以及符号所在层次和标志位特征分布权重的关联属性信息.该指标利用TF-IDF-ICD[18]特征提取算法，构造了属性隶属函数.

定义 8.符号关联指标隶属函数为：

(9)

μsk是符号s的关联度隶属函数；TFs为s的频度公式，描述Q中s个数nQs和RQt中s个数nRQts之比；IDFs是公式逆频率，N为数据库中公式总数，NsRQt为Q中出现任意符号的公式总数；ICDsk是符号频度和符号类别分布公式，当符号处于不同层次或标志位时，其权重不同；α是IDF与ICD之间的调和因子，α越大符号属性权重分布越高，ICD值越大，说明IDF对该函数影响越小.

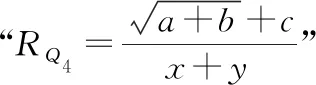
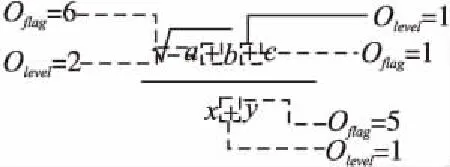
图4 RQ4的运算符关联属性示意图Fig.4 Schematic diagram of operator association properties for RQ4

4.2 数学表达式检索结果排序方法

对数学表达式检索结果进行排序的算法如算法1所示.

算法1.IVHFS的数学表达式检索结果排序算法

输入：LaTeX数学表达式Q

输出：结果表达式的排序集合rank

1.doublef[j][3]

//存放待查询式的关键字j的属性指标特征flag(f[j][0])、level(f[j][1])、len(f[j][2])、pos(f[j][3])

2.IVHFSR

//待查询式的区间值犹豫模糊集合

3.ifQ⊆RQtthen//RQt中存在子式Q

4. 按FDS解析公式

5.whilelength(Q)≠0do

6.key(i)//将Q、Q中所包含符号填入到关键词字典

7.forj=1∶4

8.f[j][i]//关键字i的属性特征矩阵

9.ifi=keythen

/*key为Q中关键字子式Q、运算符o和运算数n*/

//关键字隶属度区间值

/*子式空间结构属性隶属度区间值集合，将特征带入式(5)-式(8)所得*/

/*运算符属性隶属度区间值集合，将特征带入式(9)所得*/

/*运算数属性隶属度区间值集合，将特征带入式(9)所得*/

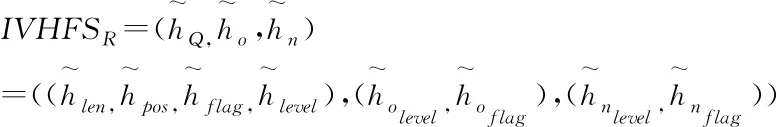
15.dis(Q，RQ)=dis(IVHFSQ，IVHFSRQ)

//Q和RQ之间的距离测度值

16.sim(Q，RQ)=1-dis(Q，RQ)

//Q和RQ的相似度，根据公式(4)所得

17.endif

18.endfor

19.endwhile

20.endif

21.RQ={RQ1，RQ2，RQ3，…}

//按相似度对结果式进行排序

22.if(sim(Q，RQt)=sim(Q，RQg))

23.e(RQ)、h(RQ)

/*待查询式的得分函数值和偏差函数值，

将IVHFSR代入公式(2)和公式(3)所得*/

24. 确定RQt、RQg的排序顺序

//按照得分和偏差值的比较法则排序

//结果表达式排序集合

26.endif

27.returnrank

在算法1中，子式属性关键字只有一个，当待查询式中存在多个Q时，仅取属性指标的最大值和最小值构成子式属性集合；但是，对于某些公式运算符和运算数的关键字不止一个，选取公式中运算符或运算数属性评价指标的最大值和最小值作为属性隶属度区间值集合即可.

5 实验分析

5.1 实验环境

在visual studio 2017和SQL2012环境下，采用C#编程语言实现数学表达式检索模型.以公共数据集NTCIR-12_MathIR_Wikipedia_Corpus[19]的31742个LaTeX格式的HTML科技文献集合中获取的528188个数学表达式作为实验数据集.

5.2 实验参数设定

1)黄骏等人[18]通过实验表明，当调和因子α=2时，可以有效增加分类属性的准确率；

2)通过对数据库中的数学表达式分析、统计、归纳属性信息，确定了位置权重系数β=0.66；数学表达式标志位和层次指标值分别如表2、表3所示，其中，x可以代表查询公式Q、运算符o以及运算数n；

表2 数学表达式标志位指标Table 2 Mathematical expressions of flag indicators

表3 数学表达式层次指标Table 3 Mathematical expressions of level indicators

所以，对μslevel和μsflag分别除以7.3、7.7方便排序.

5.3 实验结果分析

本实验主要对528188个数学公式进行分析和检索实验，以查询公式“Q2=x+y”为例，得到一个有序的有限结果表达式集合RQ2={RQ21，RQ22，RQ23，…}.其中，RQ21是集合RQ2中与Q2相似度最高的公式，且集合内相似度依次降低.表4为检索Q2时部分表达式的区间值犹豫模糊集合以及相似度.

表4 部分表达式的区间值犹豫模糊集以及相似度Table 4 Partial interval valued hesitation fuzzy sets and similarity of expression

ID是公式序号，其中，查询式的ID=1；根据公式(4)，选择不同的相似测度对表4中数据处理，当λ=1、2、3时，对应的排序结果序列分别为：

E1=(1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18)

E2=(1，2，3，4，5，6，7，8，9，10，11，12，13，15，14，16，17，18)

E3=(1，2，3，4，5，6，7，8，9，10，11，13，12，15，14，16，17，18)

专家的排序结果序列为：

EV=(1，3，2，4，5，6，7，9，8，10，11，12，14，13，15，16，17，18)

采用皮尔逊相关系数计算专家评价和本方法的排序结果序列间的相关度，两个排序结果序列之间的相关度越高，说明该评判方法越接近专家的判断.其中，皮尔逊相关系数计算公式为：

(10)

其中，ρ的取值范围为[-1，1]；

NV代表实验算法排序结果序列；

EV代表专家排序结果序列.

当λ取不同值时，部分数学表达式相似度取值如图5所示，皮尔逊相关系数分别为：

ρE1，EV=0.9938、ρE2，EV=0.9897、ρE3，EV=0.9856

通过皮尔逊相关系数和图5折线图中决策结果进行对比分析观察可以得出，当λ取不同的值时，相似度的相对大小趋势不变，因此该方法在一定程度上具有较高的普适性和可靠性.

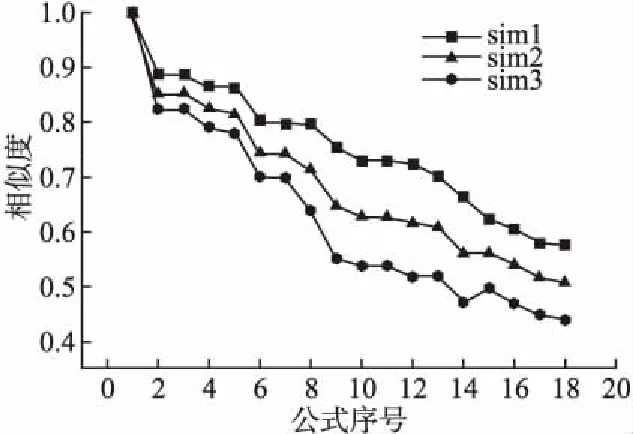
图5 部分表达式的相似度Fig.5 Partial similarity of expression

5.4 对比实验

表5 Top-5检索结果Table 5 Top-5 search results

于查询式中的符号时，两个公式相似度相同，无法确定两个公式的先后关系.比如，本文系统中第3个和第4个检索结果为并列关系，这是本实验未考虑到的地方，未来会增加包含查询公式以外符号属性的指标函数，不断完善排序效果.

5.5 检索分析

选取表4中ID值为前10的公式作为查询关键字检索，利用公式(11)得到如图6所示的查全率(Recall)和查准率(Precision).

查全率=(检索出的相关公式个数/ 系统中相关公式总数)*100%

查准率=(检索出的相关公式个数/ 检索出的公式总数)*100%

(11)

本文的平均查全率为75.8%，平均查准率为66.4%.当查询公式越简单时，系统中相关公式的数量就越多，公式的查全率就越高；而当查询公式越复杂，其系统中的相关公式数量

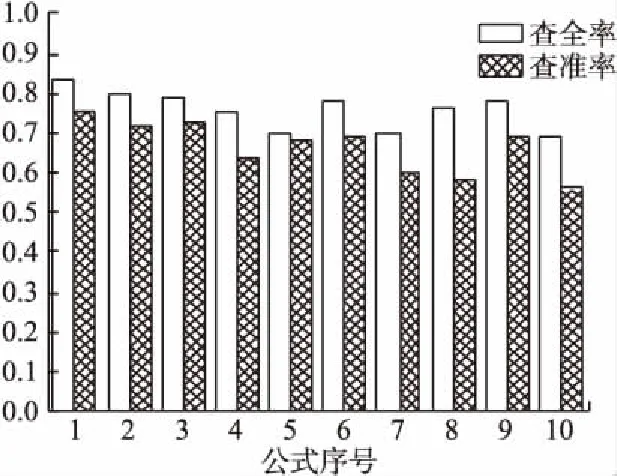
图6 系统检索查全率和查准率Fig.6 Retrieval recall and precision

就越少，所以，公式查询结果越容易产生错误，其查准率越低.

6 结论与展望

本文利用数学表达式的符号、语法和语义特征信息，引入一种IVHFS的数学表达式检索结果排序方法.该方法融合决策分析领域技术，对表达式进行多属性描述.提取表达式的子式空间结构属性、运算符关联属性以及运算数关联属性作为表达式的属性特征，并且在每个属性下都又各自增添了不同指标，从而增强属性描述的多面性和灵活性.最终为满足使用需求，获取了全面和详细的数学表达式评估信息.

本实验方法也存在一些不足:1)该实验主要针对包含式查询，所以，导致系统无法对其它比如在结构、语义等方面相似的公式进行查询，因此，具有一定的局限性;2)为了灵活满足用户查询公式的需求，在实验中可以增设其它文字信息的关键字进行以文字和公式相互融合的查询，当用户对公式认识不清时，增加文字信息来引导公式的查询，增强公式描述的准确性，使得排序结果更加合理有效.除此之外，还有其它的缺陷，在以后会不断完善实验，提高实验的排序效果.