多重调谐质量阻尼器对简支箱型梁结构低频振动控制的仿真研究*
2021-02-04张新亚雷晓燕
张新亚 雷晓燕 罗 锟
(1.广州地铁设计研究院股份有限公司,510010,广州;2.华东交通大学铁路环境振动与噪声教育部工程研究中心,330013,南昌∥第一作者,硕士研究生)
高架桥具有工后沉降低、节约土地、建设周期短等诸多优点,近年来在城市轨道交通中得到了广泛的应用[1]。然而,列车通过桥梁引起的桥梁振动问题日益突出,并且轮轨作用激起的桥梁振动还会向四周辐射低频噪声。研究表明桥梁低频结构噪声向四周传播时,衰减慢、穿透力强,更容易给人的身心健康带来长期性的危害[2-3]。因此寻求有效的振动噪声控制技术,对于保护城市环境以及促进城市轨道交通的发展都具有重要意义。
调谐质量阻尼器(TMD)是一种有效的结构振动控制设备,由附加质量块、弹簧以及阻尼等组成,属于被动式吸振器,常用于地震、风致振动的控制中。近些年在铁路简支桥梁的车致振动控制中,TMD 逐渐得到人们的关注。文献[4]以Timoshenko梁为研究对象,分析了在移动荷载下附加TMD 后的振动控制效果;文献[5]研究了TMD 对移动荷载作用下桥梁振动的控制规律;文献[6]以南京长江大桥为研究对象,研究了TMD 在该桥减振控制中的参数敏感性和控制效果。但是TMD 的鲁棒性较差,当本身的阻尼比或者主振动系统的固有频率发生改变时,使其偏离最优设计时减振性能会随之减退。文献[7]首次提出多重调谐质量阻尼器(MTMD),使得TMD 的控制效果更加稳定;文献[8]分析了MTMD 抑制铁路钢桁梁桥横向振动的振动效果,也发现相对于TMD,MTMD 可扩大减振范围、改善减振系统的鲁棒性。
目前,有关TMD 在高架桥梁中的应用研究已有较多文献报道,但是MTMD 抑制高架混凝土箱梁振动研究鲜为少见。本文利用有限元数值仿真技术,研究了MTMD 的减振效果,并探讨了MTMD的参数敏感度。研究结论可为高架桥梁的减振设计提供参考。
1 MTMD 设计理论
对于TMD 采用经典扩展定点理论[9]进行最优化参数设计。该理论认为TMD存在最优频率比α 和最优阻尼比β,计算表达式如下:
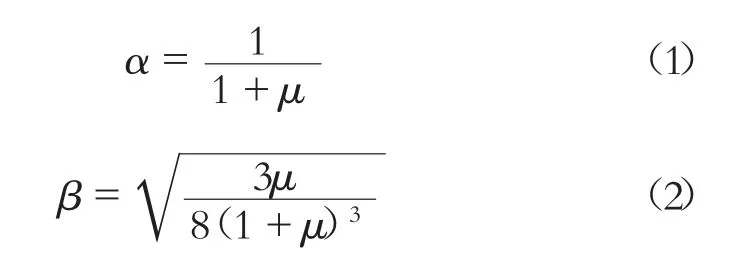
式中:
μ——TMD 的质量m 与主质量M(即箱梁的模态质量)的比值。
MTMD 的设计是利用位移振幅最小化的评价函数进行最优化设计,即考察并列设置多个调谐质量阻尼器的主振动系统位移振幅曲线的极大值,把这些极大值放在一起构成一个评价函数,利用登山法[9]进行数值解析,求解最优设计参数。
登山法是一种常用的优化算法,其原理是首先在搜索空间随机选取一点作为迭代初始点;然后在其邻域内随机产生一点,计算其函数值;若该点函数值优于当前点,则用当前点替换初始点作为新的初始点继续在邻域内搜索,否则继续在邻域随机产生另一个点与初始点进行比较,直到找到比其优秀一点或连续几次都找不到比其优秀的点则终止搜索过程。
其中求解二重调谐质量阻尼器(其μ 为μ2)的最优调谐条件如下:
1)最优频率比:
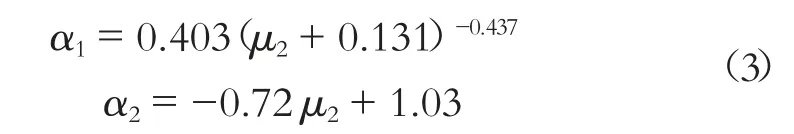
2)最优阻尼比:
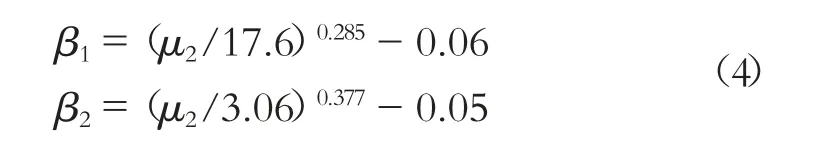
四重调谐质量阻尼器(其μ 为μ4)的最优调谐条件如下:
1)最优频率比:

六重调谐质量阻尼器(其μ 为μ6)的最优调谐条件如下:
1)最优频率比:

所以在选定μ 之后,可计算出相应的α 和β,并根据相应的α 和β 值,可计算MTMD 中阻尼器相应的阻尼C 和弹簧刚度K:

式中,f 为主结构的受控模态频率。
2 箱梁MTMD 最优参数的确定
2.1 有限元模型的建立与精度校验
基于有限元分析软件ANSYS 建立箱梁结构有限元模型如图1 所示。模型中梁体采用solid45 单元模拟,结构参数见表1 所示,其单元数为26 800,节点35 904 个。简支箱型梁长32 m,为双线行车梁型。

图1 箱梁三维有限元模型

表1 有限元模型结构参数
计算箱梁模型自由模态频率,并与文献[10]中缩尺试验模型的实测结果进行对比,基于相似比尺进行误差分析如表2 所示,发现试验结果与模态分析结果吻合良好,验证了有限元模型的精度及适用性。
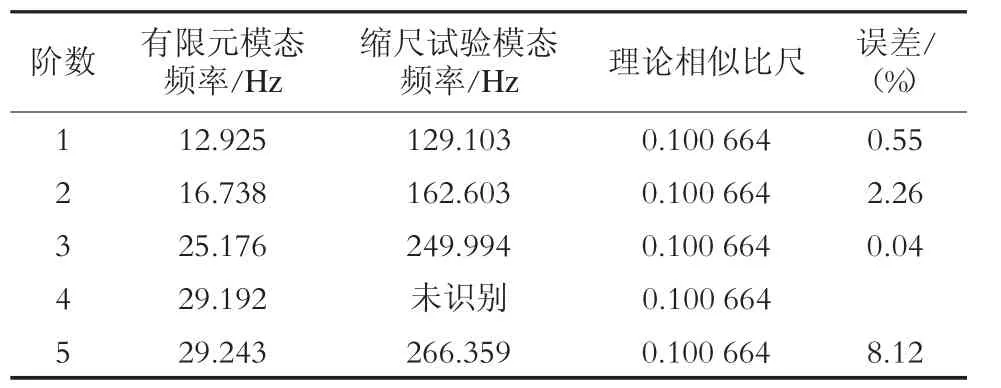
表2 箱梁结构仿真与试验模态频率对比
2.2 受控模态分析
本文通过对箱梁结构进行模态分析,采用振型贡献率确定箱梁减振受控模态[11]。振型贡献率定义为:

在箱梁底板的4 个角点建立4 个弹簧-阻尼单元Combine14 模拟桥梁弹簧支座,支座的竖向刚度为3.38×106kN/mm,阻尼为105N·s/m。对上述箱梁有限元模型进行模态分析计算,得到箱梁的前10阶固有频率及振型贡献率如表3 所示。
由表3 分析可以看出,箱梁x、y、z 方向的前10阶振型总贡献率均大于95%,即说明前10 阶的振型已经满足确定箱梁受控模态分析的需要。这里主要关注箱梁竖向的动力学响应,故只研究箱梁在竖向(y 方向)上的模态。可以发现y 方向上第2阶模态,也即一阶竖弯模态贡献率达85%,模态振型如图2 所示。故确定第2 阶为受控模态,频率为5.960 Hz。
2.3 MTMD 最优参数的确定
现阶段研究认为TMD 减振效果随质量比μ 的增加而增强,但经综合考虑控制效果、经济与结构安全等多种因素,MTMD 的μ 取值不宜过大,一般取2%~5%[12]。本文选定μ 为0.02,将μ 代入设计理论公式,计算MTMD 最优调谐参数见表4 所示。
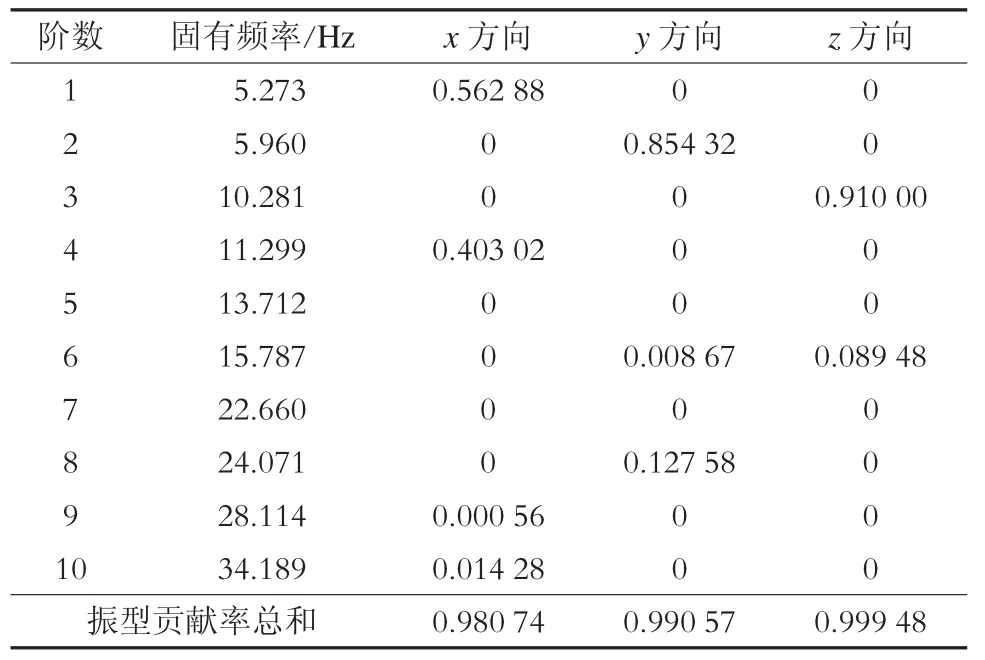
表3 箱梁自振频率及振型贡献率
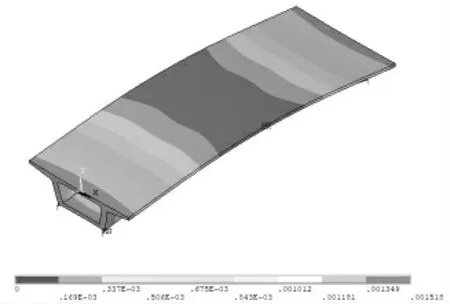
图2 受控模态振型图
3 MTMD 减振效果分析
在箱梁有限元模型中添加MTMD 减振设备,质量块选用MASS21 单元进行模拟,弹簧阻尼元件选用COMBIN14 单元模拟。将MTMD 设备悬挂于箱梁跨中截面腔内的顶板上,设计平面布置见图3所示,对应最优设计参数取值见表4 所示。选取跨中顶板421 节点为振动响应监测点,如图4 所示。
在图4 所示加载点,施加频率为6 Hz、幅值为4 600 N 的简谐荷载,通过瞬态分析计算在不同的TMD 附加个数下,振动监测点的加速度时域响应,其时程曲线如图5 所示。可以发现设置TMD对于抑制桥梁结构的共振有很好的效果,而MTMD制振效果更佳,并且随设置个数的增加,效果也增强。
图6 为设有MTMD 前后箱梁振动监测点的幅频响应。由分析可知,在一阶竖弯固有频率5.960 Hz处,谐响应幅值出现极大值。并且设置MTMD 后,固有频率附近的加速度响应明显降低,相对于未安装TMD 时,单个TMD 可使幅频响应极值减少32.7%,二重TMD 可减少33.9%,四重TMD 可减少36.4%,六重TMD 可减少36.5%。可以发现随着设置TMD 个数的增加,减振效果逐渐增强,但是四重之后制振性能增加不再明显。
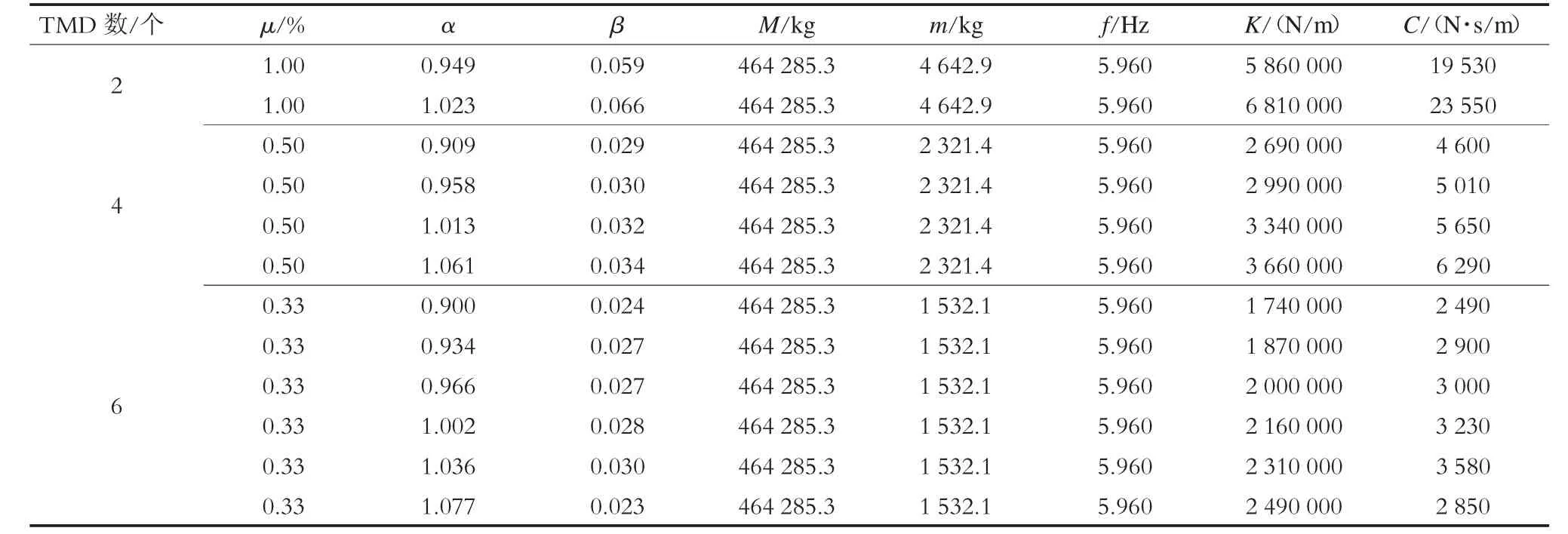
表4 MTMD 最优调谐参数
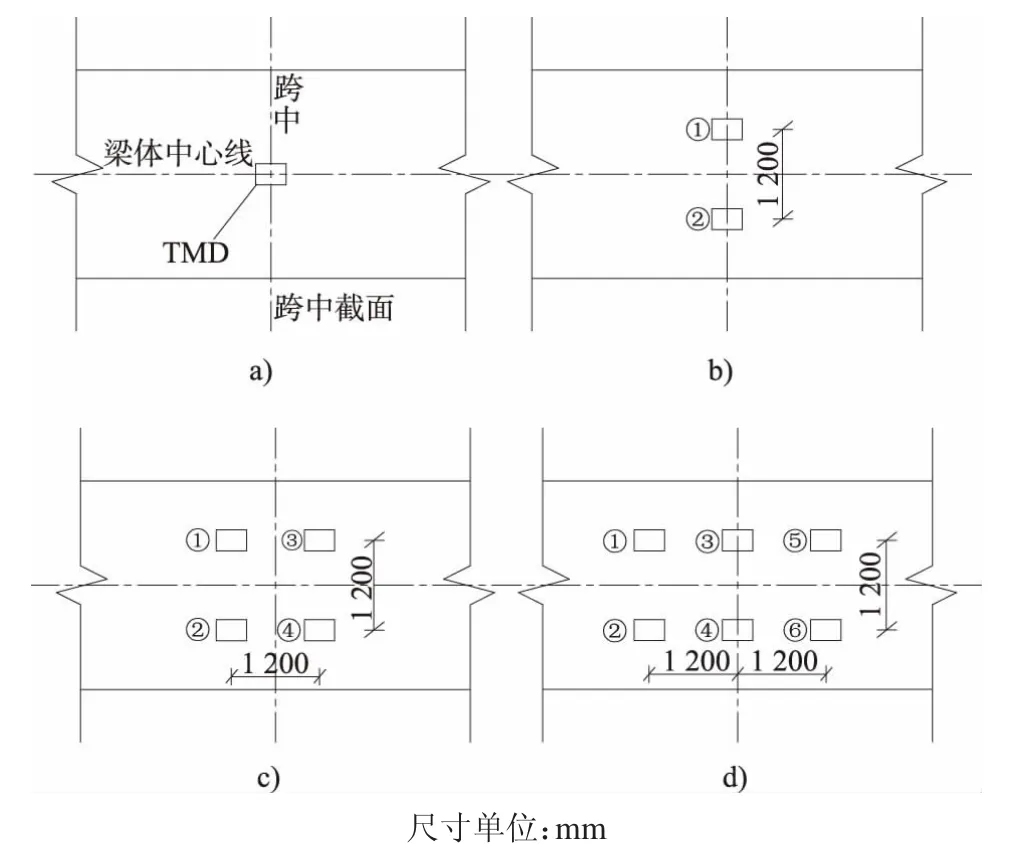
图3 MTMD 平面布置图
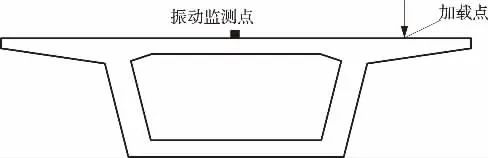
图4 跨中截面特征点
4 MTMD 参数敏感性分析
TMD 的鲁棒性体现在参数最优化设计后其控制效果在种种变化因素作用下仍能维持稳定。按照最优设计参数进行TMD 的制作,能使TMD 达到最优的吸振效果。但实际上TMD 对结构进行振动控制时,被控结构及TMD 的加工与制作过程中,不可避免地会出现参数的制作误差,故有必要去研究这些误差对减振效率的影响。即需对MTMD 设备的质量参数、刚度参数和阻尼参数进行敏感性的分析。4.1 MTMD 质量敏感性分析
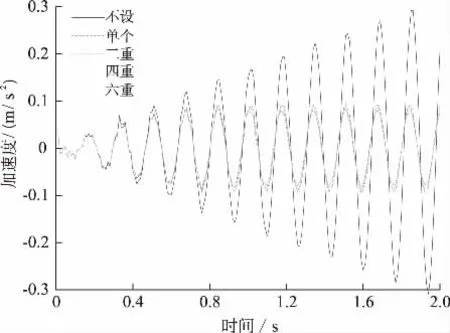
图5 设有MTMD 前后的箱梁加速度时程曲线
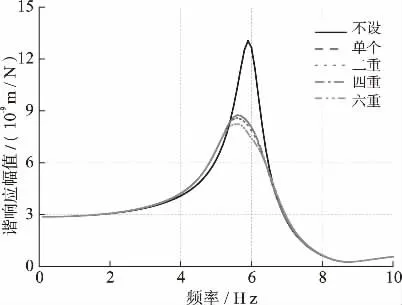
图6 设有MTMD 前后的箱梁幅频响应
现对简支箱梁桥一阶竖向振动控制问题进行质量参数偏离的敏感性分析。其中,MTMD 的质量分别按照设计质量的50%、60%、70%、80%、90%、100%、110%、120%、130%、140%、150%进行取值,设计质量即按表4 取值。进行质量参数分析时,刚度及阻尼系数均按照设计参数进行取值。计算各工况下跨中截面振动监测点的谐响应幅值,如图7 所示。
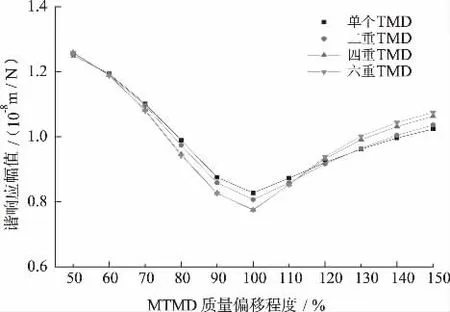
图7 MTMD 质量敏感性对比
根据图7 可以发现,随着质量向着正、负方向的偏移,谐响应幅值上升,阻尼器的减振效果均发生明显的下降。在质量发生较小程度的偏移(70% ~110%)时,调谐质量阻尼器制振性能仍然随着设置个数的增加呈升高的趋势。但是在质量偏移较大时,特别在质量取值大于120%时,可以明显发现随着设置个数增加,敏感性也相应提高。MTMD 整体制振稳定性随设置个数的增加而减弱,负向偏移稳定性较正向差。
4.2 MTMD 刚度敏感性分析
现对简支箱梁桥一阶竖向振动控制问题进行刚度参数偏离的鲁棒性分析。其中,MTMD 的刚度分别按照设计刚度的60%、70%、80%、90%、100%、110%、120%、130%、140%进行取值。进行刚度参数分析时,MTMD 的质量以及阻尼系数均按照设计参数进行取值。计算各工况下跨中截面振动监测点的谐响应幅值,进行设置不同TMD 个数下,刚度敏感性的对比(见图8)。
由图8 可以发现,随着刚度向着正、负方向的偏移,谐响应幅值上升,阻尼器的减振效果均发生明显的下降。在系统质量发生较小程度的偏移(75%~140%)时,调谐质量阻尼器制振性能仍然随着附加个数的增加呈升高的趋势。但是在质量取值小于设计质量75%时,可以明显发现随着个数增加,敏感性也相应提高,制振效果变差。MTMD 整体制振稳定性随个数的增加而减弱。
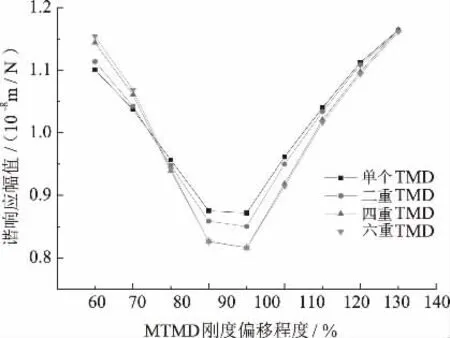
图8 MTMD 刚度敏感性对比
4.3 MTMD 阻尼系数敏感性分析
现对简支箱梁桥一阶竖向振动控制问题进行阻尼系数偏离的鲁棒性分析。其中,MTMD 的阻尼系数设置分别按照设计阻尼系数的20%、40%、60%、80%、100%、120%、140%、160%、180%、200%进行取值。进行阻尼系数偏离分析时,质量参数及刚度均按照设计参数进行取值。
计算各工况下跨中截面振动监测点的谐响应幅值(见图9)。从图9 可以看出:
1)同等μ 的情况下,MTMD 的减振效果要优于单个TMD。
2)与单个TMD 相比,MTMD 在阻尼系数发生变动的情况下,随设置的TMD 个数的增加,谐响应幅值的变动较小,意味着受环境因素的影响较小。
3)相对于单个TMD,如果将MTMD 阻尼系数设定得比最优值大一些的话,则即使阻尼值发生变化,谐响应幅值的增加也可得到抑制。
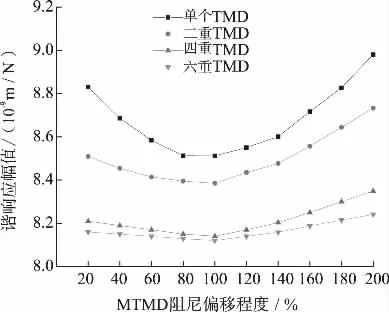
图9 MTMD 阻尼系数敏感性对比
5 结论
1)通过模态分析可确定简支箱梁的一阶竖弯模态为设置的MTMD 的受控模态,受控频率为5.960 Hz。
2)在设置TMD 质量相同的情况下,MTMD 的制振效果优于单个TMD。但发现设置4 个与6 个TMD 的制振性能差异不明显,可以认为4 个TMD效果最优。
3)质量、刚度参数灵敏度分析结果显示,MTMD 制振稳定性较单个TMD 差,设置个数越多则越明显。
4)阻尼参数灵敏度分析结果显示,MTMD 在阻尼系数发生变动的情况下,谐响应幅值较单个TMD 变动要小,随设置TMD 个数的增加,制振稳定性增强。
