基于时间序列和GRU的滑坡位移预测
2021-02-04鄢好,陈骄锐,李绍红,吴礼舟
鄢 好,陈 骄 锐,李 绍 红,吴 礼 舟
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)
1 研究背景
滑坡是一种危害极大的地质灾害,滑坡的发生往往造成公路阻断、供电供水设施毁坏、生态破坏,给人民群众生命财产安全造成极大威胁。滑坡位移预测是滑坡灾害防治的基础性工作之一[1]。
数学模型预测是当前滑坡位移预测采用的主要方法。通常来说,滑坡预测方法可分为单因素和多因素预测法。例如Verhulst模型[2-5]、GM(n,1)[6-8]等单因素法运用于滑坡预测都取得了较好效果。随着信息技术和监测技术的更新,目前更倾向于使用多因素法。杜鹃[9]等基于诱发因素的响应分析,搭建BP神经网络对滑坡位移周期项进行预测;张俊[10]等基于时间序列与PSO-SVR耦合模型,建立了周期性位移与外在因素的响应关系;周超等[11]基于小波变换和ELM模型,提出了混沌时间序列WA-ELM 滑坡位移预测模型。一般认为,当信息足够时,考虑多因素的“学习型”方法比考虑单因素的方法显得更合理。但目前这类方法多属于静态模型[12],限于隐含层网络单向传递结构特点,往往无法顾及滑坡自身演化的趋势,从而制约了模型的预测效果。随着深度学习的兴起,杨背背等[12]将长短时记忆网络应用于滑坡预测,建立了滑坡位移变化过程的动态预测模型。GRU( Gated Recurrent Unit )作为长短时记忆网络的一种优化模型,在自动化识别与分类方面取得了良好的效果[13-14],但目前在滑坡位移预测中的应用研究还相对较少。
综上所述,本文以三峡库区八字门滑坡ZG111监测点为例,依据季节性降雨与库水位变化导致滑坡的“阶跃性”特征,建立时间序列模型,将位移分解为趋势项和周期项。用灰色Verhulst模型预测趋势项,基于诱发因素建立GRU模型预测周期项,并且与传统的神经网络GRNN(Generalized Regression Neural Network)模型进行对比分析,以均方根误差RMSE和拟合优度R2评价各模型的预测精度,叠加趋势项与周期项得到累计位移预测。
2 位移分解与预测方法介绍
2.1 基于时间序列的位移分解
山体滑坡位移的产生多是由内在因素(边坡土体的性质、岩体结构、地质构造、地应力等)和外部因素(降雨、地表水和地下水的作用、地震以及工程荷载等)共同引起的[15-17]。对于八字门滑坡,内在因素是其固有变化特性,而外在因素为季节性降雨和库水位周期性变化。据此,可将滑坡总位移进行如下分解:
x(t)=p(t)+q(t)
(1)
式中:x(t)表示总位移时间序列,p(t)表示位移的趋势性部分;q(t)表示位移的周期性部分,该项位移是多种外部因素耦合的结果。
2.2 灰色Verhulst模型预测趋势项
灰色Verhulst模型建立的过程与GM(1,1)类似,根据原始数据序列x(0)得到一阶累加(1-AGO)新数据序列x(1)以及紧邻均值生成序列z(1),然后建立灰色Verhulst模型的白化微分方程:
(2)
式中:a,b为参数,由最小二乘法计算为
(3)

(4)
求解微分方程(2)可得模型的时间响应式:
(5)
对式(5)作累减还原,得到原始序列的灰色Verhulst预测模型为
(6)
2.3 基于深度学习方法预测周期项
传统人工神经网络ANN属前向神经网络,一个节点输出值只能传递给下一层网络的节点,同层之间的节点相互独立。而在递归神经网络RNN中,一个节点的输出值理论上可传递给任意节点,作为该节点的输入,在任一时刻的计算中,网络不仅受该时刻输入数据的影响,还受网络历史值的影响。基于对历史信息的记忆特性,RNN与传统ANN神经网络相比(见图1),在处理时间序列问题上凸显一定的优势。
尽管RNN能够有效处理非线性时间序列问题,但实际应用中,对于距离较远的历史信息,RNN学习能力会大大减弱[18-19]。基于以上问题,Hochreiter等提出了LSTM,结构如图2(a)所示,在RNN的基础上增加了输入门(input gate)、遗忘门(forget gate)及输出门(output gate)等记忆单元,大大提升了RNN的长时序处理能力。但LSTM模型结构过于复杂,故Cho在2014年对LSTM模型进行了优化,提出了GRU模型,包括将输入门,遗忘门、输出门变为更新门(update gate)和重置门(reset gate)以及将单元状态ct和ht并为一个状态ht。

图1 ANN与RNN对比示意Fig.1 Difference between ANN and RNN

图2 LSTM与GRU对比示意Fig.2 Difference between LSTM and GRU

rt=σ(wr[ht-1,xt])
(7)
zt=σ(wz[ht-1,xt])
(8)
(9)
(10)
yt=σ(woht)
(11)
式中:wr为重置门的权重;wz为更新门的权重;tanh表示双曲正切函数;σ为sigmoid函数。其中wz,wr,wh和w0为需要训练的参数,其中前3个需要学习的参数是拼接而来:
wr=wrx+wrh
(12)
wz=wzx+wzh
(13)
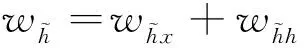
(14)
2.4 模型精度评价
预测模型的精度代表着预测值的可信度,拟合优度R2与均方根误差RMSE用来评价模型的预测效果。此外,应用相对误差和绝对误差评价具体月份的预测效果,其中拟合优度和均方根误差的计算式如下:
(15)
(16)
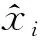
3 八字门滑坡变形概况
如图3所示,八字门滑坡位于长江北岸支流香溪河右岸,距三峡大坝38 km。地势西高东低,山前斜坡坡度约5°~30°,斜坡后部山体较陡,坡度约为42°~60°,滑体体积约为200万m3,滑体高程分布为100~250 m,其中最大横向宽度介于100~350 m。该滑体主要由破碎角砾岩和松散沉积物组成,现已存在两个滑面:下部的主滑带位于10~35 m的沉积物与基岩交界处;上部的次级滑带是沿着早期滑面滑动形成,位于滑体中上部6~8 m和底部27~33 m处[20-22]。
八字门滑坡共设置ZG110、ZG111、GSC1、GSC2等10个GPS监测点,其中ZG110,ZG111于2003年开始监测,其余的从2013年9月开始监测。本文收集到的2004年1月到2012年9月的八字门滑坡监测资料如图4所示[23]。

图3 八字门滑坡地形Fig.3 Topographic map of Bazimen landslide

图4 滑坡位移值和月降雨量Fig.4 Landslide displacement and monthly rainfall
每年的6~8月份,八字门滑坡的位移曲线呈阶梯状递增,在地表形成大量的裂隙,如图5所示,这些地表裂缝给当地居民生活带来了严重的困扰[24-25]。这一时间段,三峡库水位下降,雨量增加,位移出现明显的“阶跃性”增加,而在其他时间段,滑坡变形缓慢。根据库水位和降雨的变化规律,滑坡累计位移时程曲线可分为3个阶段。
(1) 第一阶段。2004年1月至2006年8月,库水位在135~139 m波动,此时间段水位升降具有规律性,监测点位移主要受降雨量影响,位移增长速率趋于平稳。
(2) 第二阶段。2006年9月至2008年9月,此阶段后水位上升到一个新的高度,水位的上升对坡体的渗流场和应力场以及岩土体的结构都产生较大的影响。这种影响在第一次库水位从155 m下降到145 m时较为明显。
(3) 第三阶段。2008年10月至2012年9月,库水位在145~175 m范围内波动,滑体适应了降雨与库水位的规律性变化,监测点最大位移增加速率出现在库水位下降及夏季降雨集中时段,滑坡进行了长期的应力调整,位移增长逐渐变得规律。

图5 地表裂缝Fig.5 Ground surface crack
4 位移预测
4.1 趋势项位移的提取与预测
趋势项位移反映了滑坡位移的长期变化规律,采用移动平均法分解趋势项和周期项,设原始时间序列为Si={s1,s2,…,st},趋势项的计算方法为
(17)
式中:φ(i)为趋势项位移提取值;n为周期值,鉴于三峡地区降雨量与库水位随季节呈周期性变化,这里取周期为12,提取的趋势性位移和周期性位移如图6所示。采用灰色Verhulst模型预测八字门滑坡趋势项,模型选择2009年1月至2012年1月数据作为模型训练,预测2012年2月至2012年9月的趋势项位移,每预测一月,将这组数据加入训练组,用于预测下一月位移,以保证模型输入数据的不断更新。预测结果如图7所示,监测点ZG111预测值平均相对误差为0.44,可见灰色Verhulst模型预测位移趋势项具有较好的效果。

图6 趋势项位移和周期项位移提取值Fig.6 Extracted values of trend displacement and periodic displacement

图7 趋势项位移预测结果Fig.7 Predicted values of trend displacement
4.2 周期项的预测
4.2.1影响因子的选取
影响因子的选取对滑坡位移预测的效果至关重要,八字门滑坡周期性位移的影响因素除了降雨量、库水位外,坡体的状态也会对环境变化有着不同的响应[10]。
(1) 降雨量。季节性降雨是诱导位移呈周期性变化的重要因素。一方面,降雨产生的地表水对坡面土壤有冲刷和搬运作用;另一方面,降雨入渗后改变了坡体的容重、动静水压力和岩土体强度。如图8(a)所示,由于降雨入渗是一个缓慢的过程[10],周期性位移与当月降雨量和两月降雨量变化相关性都较大,故可以选取位移时间点当月和两月的降雨量作为影响因子。
(2) 库水位。八字门滑坡土质主要为含砾黏性土,渗透性能较差。当三峡水库蓄水时,地下水向坡体内渗透,水位与滑坡体内地下水位形成负落差,对坡脚有着反压作用,有利于边坡稳定;在库水位下降时,效果相反,使滑块的变形速度加快[12]。如图8(b)所示,库水位对滑块的变形影响还有一定的滞后性,因此选择库水位高程、当月库水位变化和双月库水位变化作为影响因子。
(3) 边坡状态。坡体不同的状态也会对外界变化响应不同。当边坡处于稳定状态时,强烈的外界变化对边坡影响也较小;当滑坡处于临界状态时,轻微的外界变化也能产生巨大的影响,选取上月周期项位移量用于表征坡体状态。
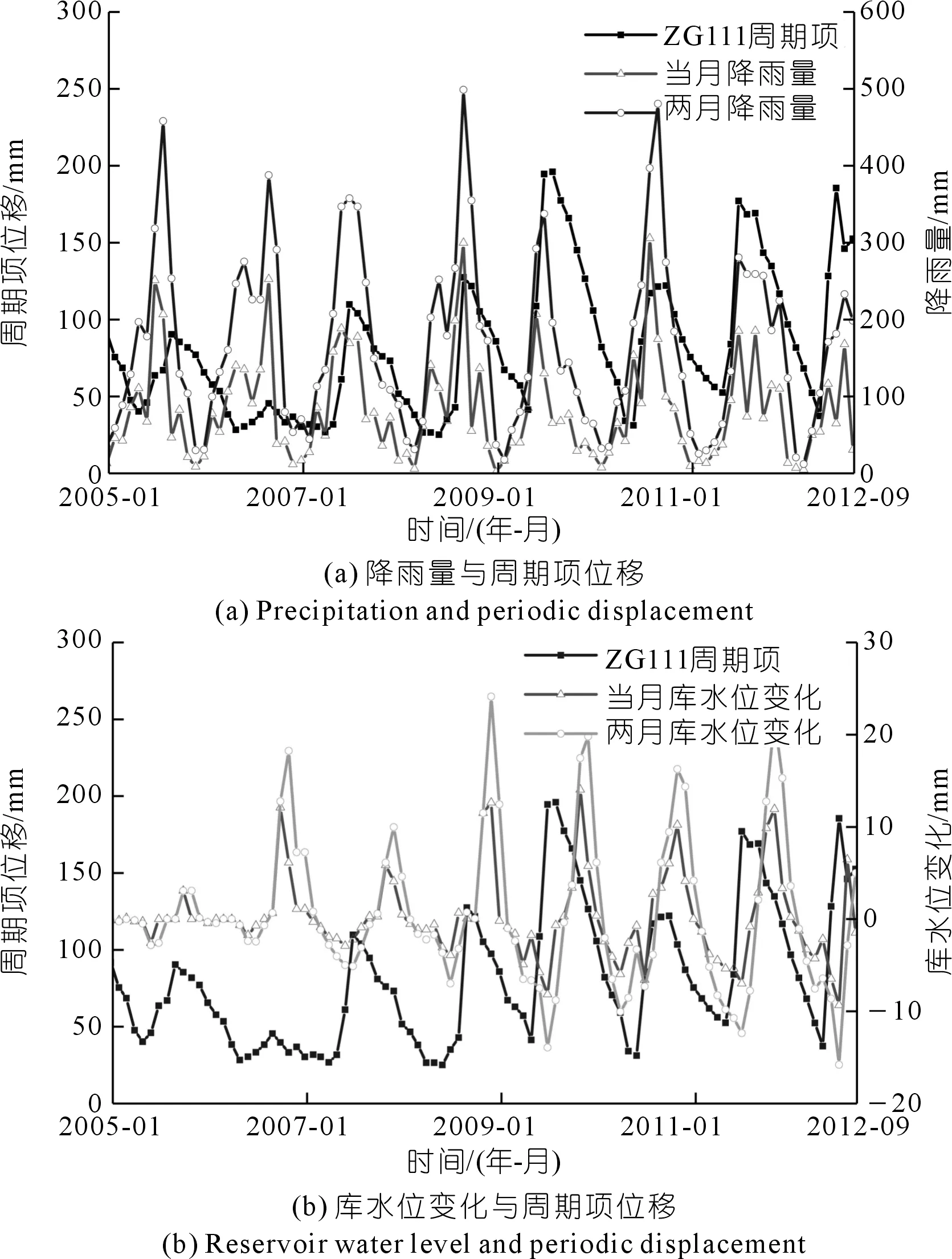
图8 周期项位移与影响因子关系Fig.8 Relationships between periodic displacement and influence factors
为验证影响因子的合理性,用灰色关联度法分析各影响因子的关联度,结果发现月降雨量、双月降雨量,库水位高程、月库水位与周期项位移关联度均超过0.6,表明所选影响因子与周期项是密切相关的。
4.2.2GRU模型的建立及参数的选取
将八字门滑坡位移数据样本划分为训练集和预测集,数据从2005年1月至2012年9月,一共93组样本数据,训练集取前85组,后8组用于检测模型的预测能力。
将选取影响因子作为输入,周期性位移作为输出。为消除量纲对预测性能的影响,将样本数据归一化到[0.1,0.9]。使用Keras框架搭建GRU模型,利用python进行程序编写。该模型包含4层神经网络,前3层为GRU层,第4层为Dense层。输入序列长度对模型的精度有重要的影响[26],控制着滑坡位移使用的历史数据的个数,通过对不同输入序列长度的试算,选择输入序列长度为3。
4.2.3周期性位移预测结果对比
为验证新模型的预测效果,采用已在滑坡预测方面取得较好效果的GRNN模型进行对比预测分析[27]。数据处理方式与GRU模型相同,GRNN模型使用MATLAB2012a进行程序编写。
周期项的位移预测结果如图9所示,各模型的预测精度见图10。

图9 周期项位移预测结果Fig.9 Predicted values of periodic displacement
GRU模型预测结果的拟合优度和均方根误差分别0.858和21.9 mm,最大误差点出现在2012年6月,此时降雨量增多,库水位下降,影响因素变化过大。尽管GRU模型仍有少数月份效果不佳,但对于三峡水库滑坡“阶跃性”特征的预测效果较好。而GRNN模型预测结果的拟合优度和均方根误差分别为0.768和25.0 mm,精度均低于GRU模型的精度。具体原因分析如下:① 由于GRNN模型的本质为静态回归模型,而GRU模型独特的门循环结构,使得当前预测值受当前输入信息和历史信息的影响,这是传统神经网络结构不具有的;② GRNN模型的训练过程是根据输入影响因素与位移的对应关系训练调整,当影响因子有较大变化时,模型的预测效果难以保证,如图10所示,在位移“阶跃”阶段,GRU模型的效果较GRNN更好。

图10 两种模型的相对误差Fig.10 Absolute error of the two models
4.3 滑坡累计位移的预测
根据时间序列的分解原理,位移趋势项与周期项之和是滑坡位移值。如图11所示,预测位移与实际位移变化接近一致,ZG111监测点预测位移的拟合优度为0.987。从预测效果来看,累计位移预测值误差最大的点与周期项误差最大的点均出现在6~7月,表明周期项的预测精度对累计位移的预测效果至关重要。
滑坡位移值由趋势项和周期项叠加得到的,趋势项变化是边坡自身发展的外在表现,灰色Verhulst属生物演化模型[3-5],对于趋势项变化过程具有较好的拟合效果。周期性位移反映了外界因素变化,而GRU模型独特的门循环结构对处理时序问题具有独特的优势。2003三峡水库首次蓄水后,位移小幅增长;2008年蓄水水位升高后,位移开始快速增长,在多年规律性的库水位调度下,逐渐形成新的平衡,位移再一次进入规律性增长[25]。由图11可知,目前累计位移的变化仍受周期项变化主导,而库水位高程为人为控制因素,故降雨量为现阶段需要密切关注的影响因子。
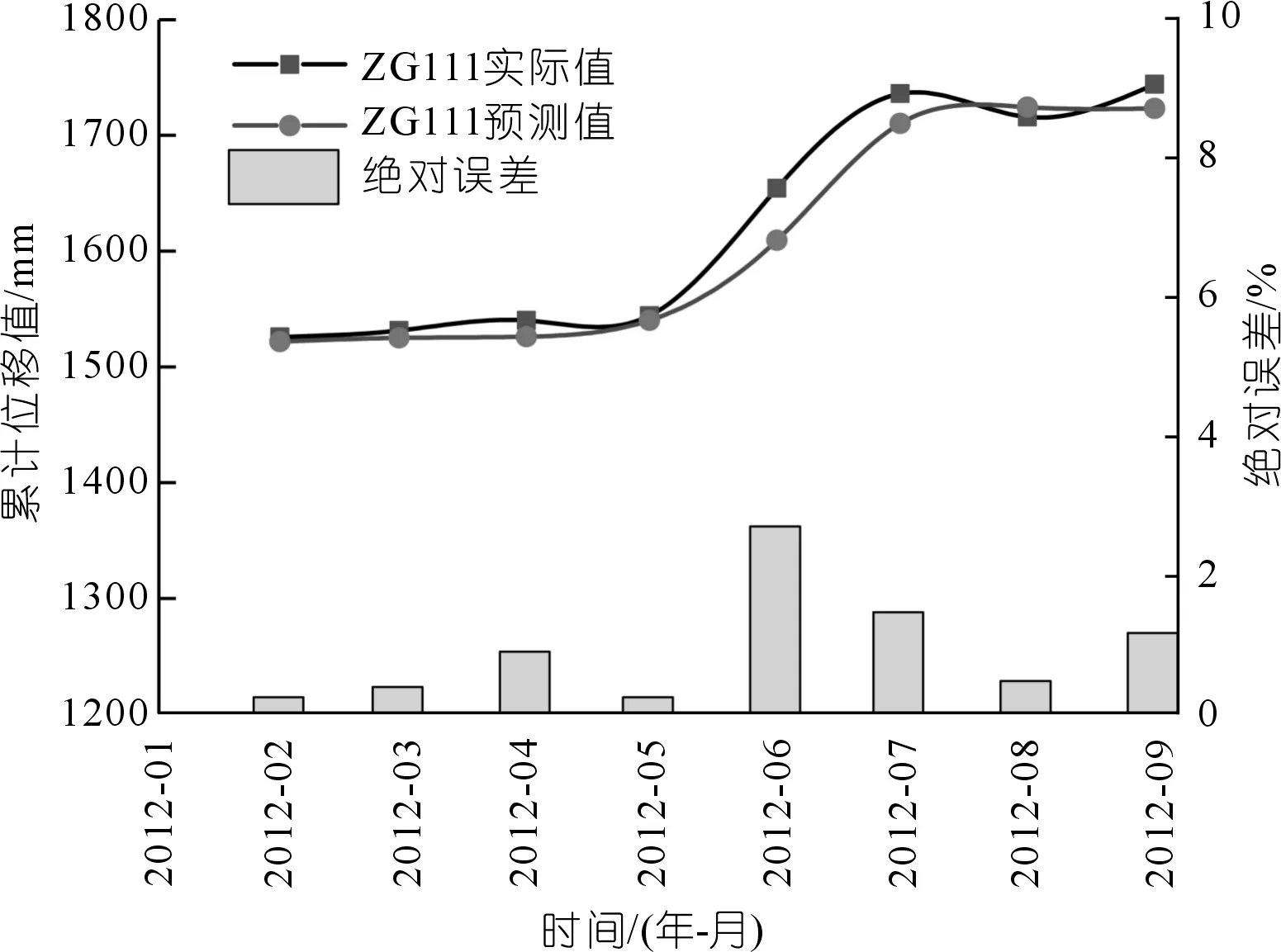
图11 滑坡累计位移实际值与预测值Fig.11 Measured values and predicted values of accumulative displacement of landslide
5 结 论
针对滑坡位移这一非线性变化时间序列,提出了一种基于时间序列和GRU网络的滑坡位移预测模型,将模型用于预测三峡库区八字门滑坡,获得以下结论。
(1) 基于时间序列分离了滑坡位移中的趋势项和周期项,灰色Verhulst模型能够较好地描述趋势项演化特征,而GRU模型能够储存和利用历史信息,在考虑影响因子的滞后性方面,不仅充分考虑了前两月的输入数据,还可以利用之前月份的输入信息,相较于传统的ANN网络,从理论上提高了有限数据的利用率。
(2) GRU模型与静态的GRNN模型相比,GRNN模型仅能考虑当前输入信息,所以在影响因子变化剧烈时,对于突变点的预测效果不佳,处理时间序列问题的能力弱于GRU模型。
(3) 三峡库区八字门滑坡位移预测工程实例表明,独特的记忆结构能够在训练过程中自动适应监测点的历史信息,实现了模型的状态反馈,适用于三峡库区“阶跃性”滑坡,可为此类滑坡位移预测提供重要的参考。
