双加权Lp 范数RPCA 模型及其在椒盐去噪中的应用

董惠雯，禹 晶，郭乐宁，肖创柏

（北京工业大学信息学部，北京100124）

引 言

主成分分析（Principle component analysis，PCA）模型可以分离观测数据中低秩的数据结构，但是对数据中大噪声异常敏感。文献［1-2］提出了鲁棒主成分分析（Robust principal component analysis，RPCA）模型，旨在分离观测数据中潜在的低秩结构与稀疏结构，对严重噪声干扰的观测数据具有鲁棒性。RPCA 模型可以应用于图像中椒盐噪声的去除［3］、监控视频背景中的前景运动目标分离［4-6］或者人物面部图像阴影与遮挡物的去除［7］等。

RPCA 模型包含两个子问题——L0范数最小化问题（稀疏恢复）与秩函数最小化问题（低秩恢复）。RPCA 模型的求解是非确定性多项式（Nondeterministic polynominal，NP）难问题，主成分追踪（Principal component pursuit，PCP）模型［5］是RPCA 模型最紧的凸近似，当秩或者稀疏程度超过阈值限制时，凸近似模型将无法准确估计低秩解与稀疏解。为此，Candes 等［8］提出了加权L1范数方法，为较大的矩阵元素分配较小的权值，抑制L1范数的过收缩问题，提升稀疏解的准确性。Gu 等提出了加权核范数最小化模型（Weighted nuclear norm minimization，WNNM）［9］，以及基于WNNM 的RPCA 模型（WNNM-RPCA）［10］，该模型利用加权核范数对秩函数进行松弛，考虑了不同秩成分的重要性，根据奇异值大小分配权值，控制对不同秩成分的惩罚，以保留更重要的秩成分，提升了低秩解的准确性。Peng 等［11］提出了一种双加权模型，同时对RPCA 模型中的稀疏项与低秩项进行加权，并结合重加权方法在迭代算法中分配权值。该模型能够同时提升稀疏解与低秩解的准确性。

L1范数是L0范数最紧的凸近似，非凸的Lp范数更接近L0范数的几何形态，p 为区间(0，1)上的任意实数。Sp范数是矩阵奇异值的Lp范数，0 ＜p ＜1，与核范数相比，非凸的Sp范数更接近秩函数的几何形态。由于这种广义的范数模型并不严格符合范数的数学定义，因此也称为伪范数或拟范数。Zhang等［12］通过实验证明，与核范数相比，非凸的Sp范数能够更准确地对数据的低秩性进行建模。Xie 等提出了加权Sp范数最小化模型（Weighted Schatten p-norm，WSNM）［13］，利用加权Sp范数对秩函数进行松弛，更准确地抑制对较大奇异值的过度收缩。WSNM 模型使用L2范数建模数据保真项，能够较好地抑制图像中的高斯噪声，但是对较大的稀疏噪声较为敏感。为此，基于WSNM 的RPCA 模型（WSNM-RPCA）［14］利用L1范数约束稀疏成分；Chen 等［15］提出了基于L1范数的WSNM 模型（WSNM based L1-norm，WSNM-L1），采用L1范数建模数据保真项。

本文提出一种双加权Lp范数模型（Dual-weighted Lp-norm，DWLP），同时提升了矩阵秩估计和稀疏估计的准确性。该算法结合加权算法与Lp范数，利用加权Sp范数低秩项和加权Lp范数稀疏项分别对RPCA 框架中的低秩恢复问题和稀疏恢复问题进行建模，使其更接近秩函数最小化问题和L0范数最小化问题的解，有效抑制凸近似模型的过度收缩。结合图像的非局部自相似性，通过构建相似图像块组，将双加权Lp范数模型应用于椒盐噪声的去除中，估计低秩的图像结构与稀疏的椒盐噪声，从稀疏噪声中分离低秩的图像结构，从而恢复或重建原始的无噪图像。

1 RPCA 模型

RPCA 模型旨在利用数据矩阵的低秩性和误差矩阵的稀疏性，从稀疏的误差中恢复出本质上低秩的数据矩阵。假设观测数据矩阵为X ∈Rm×n，低秩矩阵为L ∈Rm×n，稀疏矩阵为S ∈Rm×n，RPCA 模型定义为

式中：rank(L)为矩阵的秩函数，定义为矩阵中非0 奇异值的个数，约束矩阵的低秩性约束误差数据的稀疏程度，这里借用L0范数描述矩阵的稀疏性；λ＞0 为正则化参数。

由于秩函数rank(L)与L0范数的求解是NP 难问题，通常用核范数对rank(L)进行凸松弛，用L1范数对L0范数进行凸松弛，将RPCA 模型转换为求解如下的凸优化问题，通过最小化L1范数与核范数的组合分解矩阵［1，2，5，16］，即

PCP 模型通过L1范数约束稀疏成分S 的稀疏性与低秩成分L 的低秩性，通常使用软阈值算子近似求解L1范数最小化问题［17］，使用奇异值软阈值算子近似求解核范数最小化问题［18］。凸近似模型容易导致过收缩问题，影响解的准确性。软阈值算子以λ 为阈值，对每一个满足|xi，j|＞λ 的元素惩罚相同的λ，当|xi，j|小于阈值时，输出的最优解si，j=0。绝对值较大的矩阵元素在L1范数最小化问题中会受到比L0范数更大的惩罚，导致过收缩问题，影响稀疏解的准确性。矩阵的秩函数等价于奇异值的L0范数，矩阵的核范数等价于奇异值的L1范数。核范数最小化问题利用奇异值软阈值算子求解，也会造成对矩阵中较大奇异值的过度收缩。矩阵的奇异值隐含着重要的成分信息，且重要性和奇异值大小正相关。奇异值的过度收缩会影响低秩矩阵的重建，降低低秩解的准确性。

Gu 等［10］提出了基于WNNM 的RPCA 模型WNNM-RPCA，即

Xie 等［14］利用Sp范数代替核范数对秩函数进行松弛，并结合加权方法，提出了基于WSNM 的RPCA 模型WSNM-RPCA，即

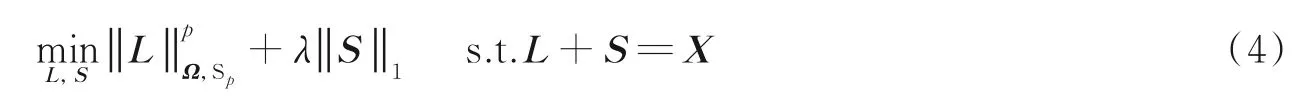
Peng 等［11］同时对RPCA 模型中的稀疏项与低秩项进行加权，提出了双加权模型，即

2 双加权Lp 范数RPCA 模型

为了解决凸近似模型对稀疏解与低秩解的过度收缩，现有的方法提出了多种改进的RPCA 模型，对L0范数和秩函数rank(·)进行松弛。本文提出了一个广义的RPCA 框架——双加权Lp范数RPCA模型DWLP，利用加权Lp范数和加权Sp范数［13］分别对RPCA 模型中的稀疏项和低秩项进行建模。

2.1 模型的建立

在RPCA 框架下，DWLP 模型利用加权Lp范数最小化模型估计稀疏恢复问题，利用WSNM 模型估计低秩恢复问题。DWLP 模型定义如下

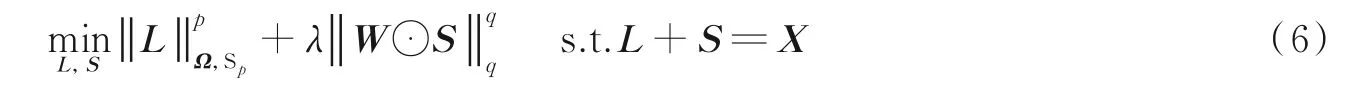
加权Lp范数通过为较大的矩阵元素分配较小的权值，控制对较大元素的惩罚力度，削弱元素值对矩阵稀疏性的影响，并采用非凸的Lp范数近似L0范数的几何形态，能够有效抑制过收缩问题，更准确地估计稀疏解。加权Sp范数根据奇异值大小分配权值，削弱对较大奇异值的惩罚，保护更重要的秩成分，并利用非凸的Sp范数近似秩函数的几何形态，提高了低秩解的准确性。因此，DWLP 模型利用加权方法与Lp范数约束目标函数中的低秩成分与稀疏成分，有效抑制过收缩问题，增强了稀疏矩阵S 的稀疏性与低秩矩阵L 的低秩性。

DWLP 模型可以看作是一种广义的低秩-稀疏分解模型，目前用于近似RPCA 模型的PCP 模型［5］、WNNM-RPCA 模型［10］、WSNM-RPCA［14］模型和Peng 等提出的双加权模型［11］均是DWLP 模型的特殊情况：

（1）当式（6）中Ω 和S 权值ωi=wi=1 并且p=q=1 时，DWLP 模型退化为PCP 模型；

（2）当式（6）中S 的权值wi=1 并且p=q=1 时，DWLP 模型退化为WNNM-RPCA 模型；

（3）当式（6）中S 的权值wi=1 并且q=1 时，DWLP 模型退化为WSNM-RPCA 模型；

（4）Peng 等［11］提出的模型是DWLP 模型在p=q=1 时的特殊情况，本文将其简写为DWLP（p=q=1）。

与仅处理低秩解过收缩的WNNM-RPCA 模型和WSNM-RPCA 模型，以及基于L1范数的双加权模型相比，本文模型能够更有效地抑制凸近似模型的过收缩问题。

2.2 模型的求解

DWLP 是非凸问题，无法直接求解。将式（6）写为增广拉格朗日形式为

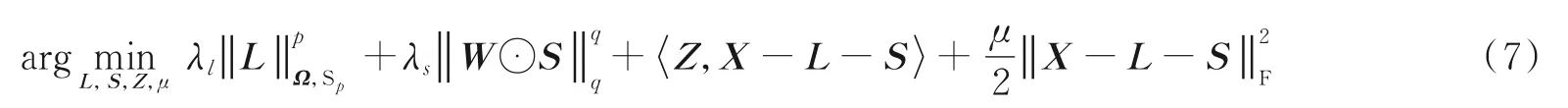
本文利用交替方向乘子法（Alternating direction method of multipliers，ADMM）求解式（7）［21］，通过交替迭代的方式更新L、S、Z 和μ 为

式中k 为迭代次数。稀疏矩阵S 和低秩矩阵L 估计是两个独立子问题，以下是具体求解过程。

（1）固定L 和Z，估计稀疏矩阵S 为

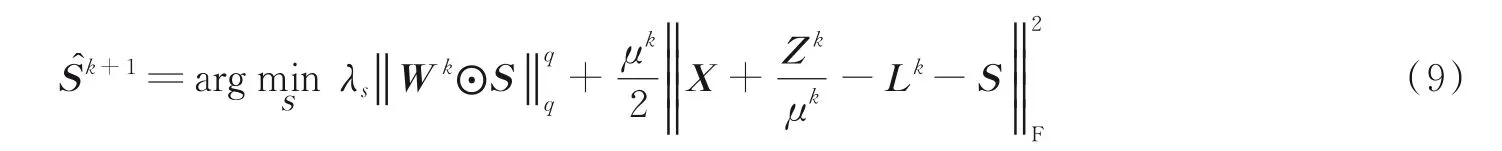
令Fk=X +Zk/μk-Lk，Φk=λsWk/μk，将式（9）写为

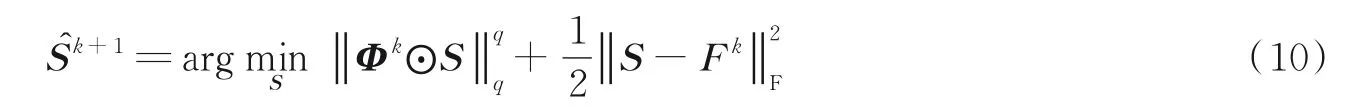
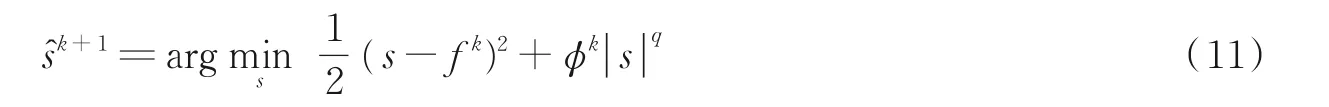
式（11）是Lp范数最小化问题，本文利用Chartrand 等提出的p-shrinkage 算子近似计算Lp范数最小化问题的闭合解［22-23］为

（2）固定S 和Z，估计低秩矩阵L 为

令Tk=X +Zk/μk-Sk+1，Ψk=λlΩk/μk，将式（13）写为

Tk的奇异值分解为Tk=UΣkVT，奇异值对角矩阵其中为的第 i 个奇异值。 低秩矩 阵的奇异值分解 为的第i 个奇异值为

本文仍利用p-shrinkage 算子近似计算式（15）中Lp范数最小化问题，其闭合解为

3 实验结果与分析

本文利用图像的非局部自相似性构建相似图像块组，将DWLP 模型应用于椒盐噪声的去除，通过在不同椒盐噪声水平下的去噪实验验证本文DWLP 模型的有效性。

3.1 DWLP 模型在椒盐去噪中的应用

椒盐噪声是一种常见的稀疏噪声，主要源于电荷耦合器件的坏点或远距离传输的脉冲干扰。脉冲干扰通常比图像信号的强度大，在图像中脉冲噪声总是数字化为最小值或最大值。基于双加权Lp范数的椒盐去噪算法主要包括以下3 个步骤：（1）利用预处理图像匹配相似图像块，生成相似图像块组；（2）利用DWLP 模型对相似图像块组进行低秩-稀疏分解；（3）聚合图像块，输出去噪重建图像。

首先，为减少椒盐噪声对相似块匹配的干扰，采用中值滤波处理观测图像I ∈Rm×n，生成预处理图像I′。在观测图像与预处理图像中以c×c 为图像块尺寸，s 为步长（即每相隔s 个像素抽取一个图像块），进行图像块划分。在预处理图像中计算第i 个图像块与其他图像块间的欧氏距离，并在观测图像中取出欧氏距离最小的K 个图像块，经过向量化表示，构成相似图像块组Xi=表示第i 个图像块的第j 个相似图像块，其中j=1，2，…，K。

其次，将相似图像块组Xi作为DWLP 模型的输入，利用2.2 节中的求解方法估计Xi中的低秩图像成分与稀疏噪声成分

3.2 定量与定性比较

本文实验在Set12、Kadak24 以及BSD200 等数据集中随机选取10 幅分辨率为256像素×256像素的灰度图像作为测试图像（图1），并通过加入不同水平的椒盐噪声，生成有噪的观测图像。

图1 测试图像Fig.1 Test images

将本文模型与PCP 模型［5］、WNNM-RPCA 模型［10］、WSNM-RPCA 模型［14］、DWLP（p=q=1）模型［11］，以及WSNM-L1模型［15］进行比较。同时采用峰值信噪比（Peak signal to noise ratio，PSNR）［24］和结构相似度（Structural similarity index metric，SSIM）［25］作为客观质量评价指标。PSNR 值和SSIM 值越大，表示图像失真度越小，去噪图像质量越好。

表1 定量比较了不同椒盐噪声概率P 情况下各种方法的去噪结果。在10%椒盐噪声概率的情况下，DWLP 模型的PSNR 值分别高出PCP、WNNM-RPCA、WSNM-RPCA、WSNM-L1和DWLP（p=q=1）约7.880、7.300、7.029、8.817 和0.269 dB；而在30%椒盐噪声概率的情况下，DWLP 模型的PSNR值 分 别高出PCP、WNNM-RPCA、WSNM-RPCA、WSNM-L1和DWLP（p=q=1）约3.833、3.847、3.667、4.869 和0.456 dB。通过实验可得出结论：首先，强度较大的椒盐噪声破坏了稀疏先验与图像低秩性，PCP 模型的复原性能较差；其次，DWLP 模型的PSNR 和SSIM 均高于其他模型的平均水平，表明使用加权Lp范数同时处理低秩成分与稀疏成分能够更准确地重建图像的低秩结构；最后，随着噪声水平的增加，当椒盐噪声概率达到50%时，噪声的稀疏性降低，DWLP 模型中p 和q 的取值接近于1，DWLP（p=q=1）与DWLP 的客观评价指标相当。

表1 不同椒盐噪声概率情况下各种去噪方法的PSNR/SSIM 比较Table 1 Comparison of different denoising methods under different salt-and-pepper probabilities in terms of PSNR/SSIM

续表

图2～4 为10%、30%与50%的椒盐噪声强度下各种方法在图像Plants、House 和Monarch 上的去噪结果。图2～4 中的（a）为真实无噪图像，（b）为不同噪声水平下的观测图像，（c～h）分别为PCP［5］、WNNM-RPCA［10］、WSNM-RPCA［14］、WSNM-L1［15］、DWLP（p=q=1）［11］和DWLP 模型的去噪图像。图中红色框部分为绿色框部分的放大视图。通过观察图2 中红色框部分对植物枝叶的放大视图，可以发现图2（g）中的DWLP（p=q=1）和图2（h）中的DWLP 能够清晰地重建图像中植物的枝叶部分，而其他算法均造成了一定程度的失真与模糊。DWLP 和DWLP（p=q=1）能够同时提升对模型低秩项与稀疏项的估计，有助于更准确地重构图像的低秩结构。与DWLP（p=q=1）相比，DWLP 的去噪图像不仅具有更高的PSNR 和SSIM 值，而且保留了更多的细节，对植物枝叶区域的复原情况更接近真值图像。通过观察图3 中红色框部分对窗口墙体的放大视图，发现仅有DWLP 的去噪图像能够较为清晰地重建图像中的窗棂结构和砖墙纹理，而其他方法均产生了不同程度的模糊或者噪声残留。通过观察图4 中红色框部分对翅膀纹理区域的放大视图，可以发现高密度噪声对观测图像中的纹理细节损毁严重，与其他去噪方法相比，本文算法能够更好地保持蝴蝶翅纹的细节。

图2 Plants 图像去噪结果（10%椒盐噪声）Fig.2 Denoised results on image Plants (10% salt-and-pepper noise)

图3 House 图像去噪结果（30%椒盐噪声）Fig.3 Denoised results on image House (30% salt-and-pepper noise)

图4 Monarch 图像去噪结果（50%椒盐噪声）Fig.4 Denoised results on image Monarch (50% salt-and-pepper noise)

上述实验结果表明，本文算法不仅具有较高的PSNR 和SSIM 值，而且具有更清晰的视觉效果，能够有效地保持图像细节，与PCP、WNNM-RPCA、WSNM-RPCA、WSNM-L1和DWLP（p=q=1）算法相比具有更好的去噪性能。

同时，本文模型也具有相对较低的时间复杂度。本文采用了具有闭合解的p-shrinkage 算子估计Lp范数最小化问题的闭合解，与采用迭代方式估计数值解的WSNM-RPCA 与包含重加权运算的DWLP（p=q=1）相比，减少了大量的迭代计算。DWLP 模型的时间复杂度为O(min{c4K，K2c2} +3c2K+1)，与WNNM-RPCA 模型和PCP 模型的时间复杂度相同。

3.3 奇异值过收缩分析

采用凸近似方法求解RPCA 模型容易导致过收缩问题，影响对相似图像块组奇异值的估计。矩阵奇异值越接近真实值，对低秩图像成分的估计越准确，去噪重建图像的质量越高。本节将通过两组矩阵奇异值分解实验分析RPCA 框架下的去噪模型对图像低秩结构的估计情况。

图5（a）和（c）为10%椒盐噪声下的Goldhill 图像和30%椒盐噪声下的Barbara 图像，利用红色框标记的图像块以及绿色框标记的相似图像块可以组成一个相似图像块组，在两幅观测图像中随机选择10个相似图像块组作为观测数据，每个观测矩阵中包含64 个8像素×8像素的相似图像块，分别使用PCP模型［5］、WNNM-RPCA 模型［10］、WSNM-RPCA［14］模型、双加权模型（DWLP（p=q=1））［11］与DWLP模型估计观测矩阵的奇异值。图5（b）和（d）为不同模型复原结果的奇异值分布情况。其中，PCP 模型（绿色线）的结果明显小于矩阵秩的真实情况（红色线），说明PCP 模型会过度收缩矩阵的奇异值。WNNM-RPCA 模型（蓝色线）一定程度上抑制了对较大奇异值的过度收缩，对秩成分的估计较为准确。而结合Sp范数的WSNM-RPCA 模型（青色线）的结果则更贴近矩阵秩的真实情况，说明Sp范数方法具有更好的近似效果。DWLP（p=q=1）模型（黄色线）与DWLP 模型（品红色线）可以同时处理对低秩成分与稀疏成分的过收缩问题，复原结果明显优于WNNM-RPCA 模型。与DWLP（p=q=1）模型相比，DWLP 模型对较小奇异值的估计更接近真实情况，获得了更准确的估计结果。实验结果表明，本文模型与其他模型相比，能够更有效地抑制过收缩问题，准确地估计观测矩阵的奇异值。

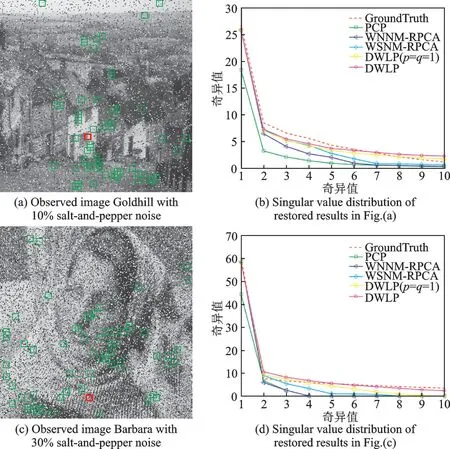
图5 低秩矩阵的奇异值分析Fig.5 Singular value analysis of low rank matrices

3.4 参数影响的分析

本文算法经验地设置图像块的尺寸为8像素×8像素，抽取步长为4 像素，相似图像块的数量K 为64；而稀疏约束Lp范数中的q、低秩约束Sp范数中的p、正则化参数λs和λl，以及ADMM 算法中的最大迭代次数Kmax等参数通过参数实验确定。

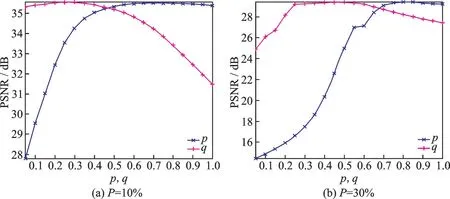
图6 不同椒盐噪声概率下p 和q 的取值对复原结果的影响Fig.6 Influence of different values of p and q on the recovery results under different salt-and-pepper probabilities

在稀疏约束Lp范数中的q 与低秩约束Sp范数中的p 的参数实验中，p 和q 的取值范围均为0.1～1，采样间隔为0.1。图6（a，b）分别为椒盐噪声概率P=10%和P=30%的情况下，p 和q 的取值对复原结果的影响。此外，分析了稀疏和低秩正则化参数λs和λl的参数实验，将低秩项的正则化参数λl设置为0.1，图7（a，b）所示为椒盐噪声概率P=10%和P=30%的情况下λs的取值对复原结果的影响。表2给出了椒盐噪声概率分别为10%、20%、30%、40%和50%的情况下稀疏约束Lp范数中的q、低秩约束Sp范数中的p 以及正则化参数λs的取值。

最大迭代次数Kmax是与算法收敛性相关的参数。由于DWLP 是非凸模型，难以从理论上证明算法的全局收敛性。因此，本文通过实验分析迭代次数对复原结果的影响。如图8 所示，当迭代次数分别达到5、10、15、20、25、30、35 和40 时，算法的平均PSNR 值为20.84、27.87、31.35、32.67、33.33、33.39、33.40和33.39 dB。通过观察发现，当迭代次数大于30 时，PSNR 值的增量变得很小，算法趋于收敛。因此，本文取Kmax=30 以避免不必要的迭代计算。

图7 不同椒盐噪声概率下λs 的取值对复原结果的影响Fig.7 Influence of different values of λs on the recovery results under different salt-and-pepper probabilities

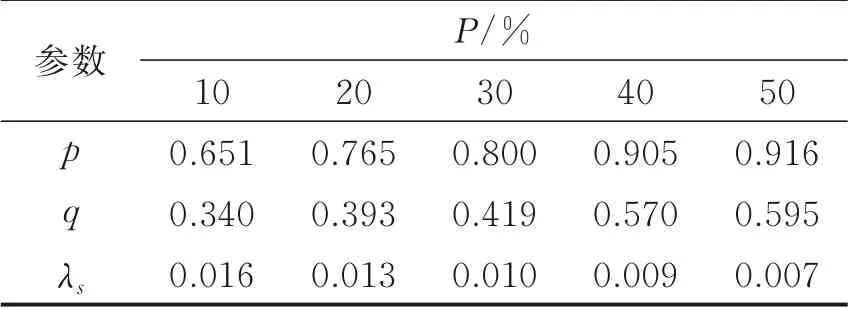
表2 不同椒盐噪声概率情况下的参数设置Table 2 Parameter setting with different saltand-pepper probabilities

图8 最大迭代次数对复原结果的影响Fig.8 Influence of the maximum number of iterations

4 结束语

为了抑制L1范数的过收缩问题，结合加权算法与非凸的Lp范数，本文提出了双加权Lp范数RPCA模型DWLP，在RPCA 框架下利用加权Lp范数和加权Sp范数建模稀疏恢复问题和低秩恢复问题，并采用ADMM 算法结合p-shrinkage 算子进行求解。将该模型应用于椒盐噪声的去除实验，结果验证了本文模型的有效性，并通过奇异值过收缩分析说明了该模型的解更接近秩函数最小化问题的解和L0范数最小化问题的解，有效抑制凸近似模型的过收缩问题。