一种基于张量分解的医学数据缺失模态的补全算法

刘 琚，杜若画，吴 强，何泽鲲，于璐跃

（山东大学信息科学与工程学院，青岛266237）

引 言

随着医学技术的发展，磁共振（Magnetic resonance imaging，MRI）技术已广泛应用于临床的疾病诊断，MRI 影像也成为辅助医生进行肿瘤分级的重要参考依据。由于不同模态的MRI 影像能够突出肿瘤不同的信息与特点，医生在肿瘤分级时会结合多个模态的MRI 影像进行诊断。然而，在实际的MRI 影像采集过程中，例如病人头部抖动或缺少某项检查，会导致数据的部分缺失。这些缺失数据在训练模型时被舍弃，造成了数据的浪费，不利于分类结果。为了有效利用这些缺失的数据，减少小样本问题的影响，研究人员提出了许多方法，其中对缺失数据进行补全是有效方法之一［1-3］。传统的缺失补全算法包括：期望最大化算法［4］、奇异值分解算法、邻近算法［5］和矩阵补全［6-7］。但是，这些方法无法有效恢复块状缺失数据，并且对于整个模态的缺失，估算大量缺失值会导致算法性能不稳定。为了应对上述情况，文献［8］提出了基于多向延迟嵌入的Tucker 分解算法，考虑张量嵌入空间的低秩模型，但该方法并未考虑到提取特征和补全张量过程中可能出现的噪声。

本文提出了一种基于多向延迟嵌入的平滑张量补全算法（Multi-way delay-embedding transform smooth PAPAFAC tensor completion，MDT-SPC）。通过对输入的不完整张量使用多向延迟嵌入转换，得到不完整的Hankel 张量，然后利用平滑CP 分解［9］来恢复不完整张量的缺失部分，最后使用多向延迟嵌入的逆过程，得到最终的补全后的张量。该方法能够有效针对数据呈条状或块缺失的情况，并且当提取特征和补全张量的过程中出现噪声时，平滑约束有助于消除计算过程中产生的非平滑项。实验部分采用BraTS2017 作为训练和测试数据集，并与多种传统方法和基于多向延迟嵌入的Tucker 分解算法进行比较。实验结果表明本文提出的脑胶质瘤分类方法可以获得更高的识别准确率。

1 基于多向延迟嵌入的Tucker 分解算法

基于多向延迟嵌入的Tucker 分解算法由3 步组成：（1）使用多向延迟嵌入转换［8］，输入待补全的张量，输出不完整的Hankel 张量；（2）通过Tucker 低秩分解［10］来恢复不完整张量的缺失部分；（3）使用多向延迟嵌入的逆过程［8］，得到最终的补全后的张量。

1.1 多向延迟嵌入及其逆变换

假设向量为v=(v1，v2，…，vL)T∈RL，则v 对应的标准延迟嵌入变换为

式中τ 为延迟嵌入变换的重复次数。标准延迟嵌入变换Hτ(v)=fold(L，τ)(Sv)，正向变换的过程是复制和折叠，而逆变换可以分解为矢量化运算和Moore-Penrose 伪逆S†：=(STS)-1ST。因此，Hankel 矩阵VH的逆延迟嵌入变换为

多向延迟嵌入变换可以表示为Hτ(T )=fold(I，τ)T ×1S1×2S2…×NSN，符号“×1”“×2”，“×N”分别代表张量与矩阵在第N 阶上的乘法操作，最后，张量的逆多向延迟嵌入变换为其中

1.2 增秩Tucker 分解

T ∈RI1×…×IN和Q ∈{0，1}I1×…×IN分别为不完整张量和掩模张量，经过多向延迟嵌入转换之后得到TH=H(T )∈RJ1×…×JM和QH=H(Q)∈{0，1}J1×…×JM，其中M ≥N。基于Tucker 分解模型得到TH的低秩近似，采用交替最小二乘求解，并引入辅助变量来简化优化过程。

基于Tucker 的张量补全方法的一个难点在于如何确定适当的秩(R1，…，RM)，算法采用一种“秩递增”的方法来确定最佳秩，主要思想是张量应通过比其目标秩更低的秩近似来初始化。步骤如下：首先对于所有的m 初始化Rm=1，然后使用(R1，…，RM)计算获得和X =G×{U}，最后检查噪声条件其中表示张量的Hadamard 乘积。若满足则终止算法，否则选择增加的模式m′和增加的Rm′，重新计算和X =G×{U}。

2 基于多向延迟嵌入的平滑张量补全算法

增秩Tucker 分解采用了较为新颖的秩逼近策略，但是并未考虑提取特征和补全张量过程中出现的噪声，而平滑特性在图像处理中具有很好的可用性。当计算过程产生噪声时，平滑约束有助于消除计算过程中产生的非平滑项，因此在进行多向延迟嵌入操作后，对折叠数据采用平滑CP 分解模型［9］进行张量补全。

2.1 平滑CP 分解模型

平滑CP 分解的优化问题［9］可表示为

式中：X 为恢复的完整张量，其中的缺失元素由CP 分解估计值Z 来填充；Ω 表示T 的可用元素索引，即未缺失数据的坐标，表示T 缺失元素的索引；ρ=[ρ(1)，ρ(2)，…，ρ(N)]T表示平滑参数；p ∈{1，2}代表用来选择平滑约束类型的参数；矩阵L(n)∈R(In-1)×In代表平滑约束矩阵。

2.2 算法求解

对目标函数使用分层交替最小二乘法求解，以因子矩阵为单元逐一更新，分别处理每个因子矩阵的规范约束为

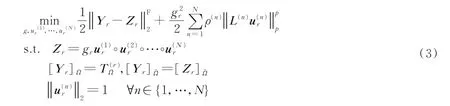
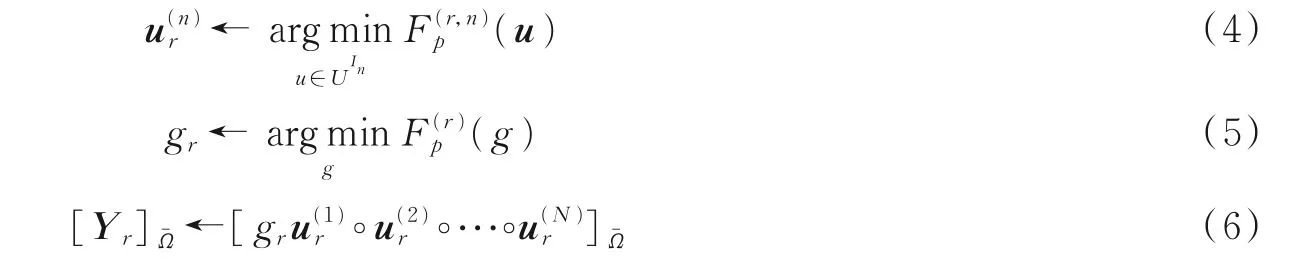
式中

使用uk和vk分别代表第k 次更新的为目标函数的梯度，因此得到uk+1的更新公式

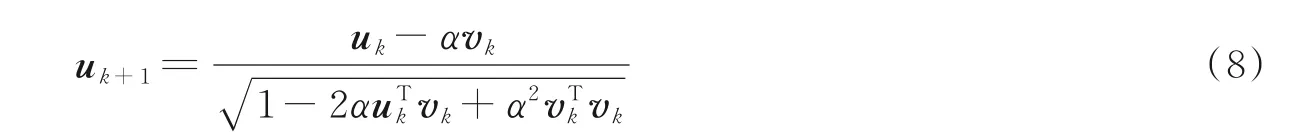
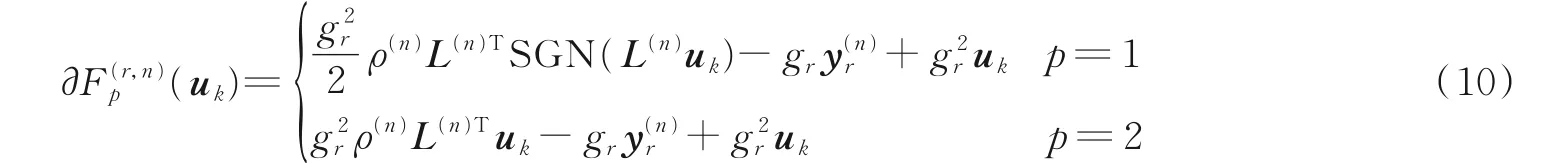
式中SGN(x) =[sgn(x1)，sgn(x2)，…，sgn(xJ)]T，其中

本文算法过程示意图如图1 所示，计算步骤如下：

(1）Hτ(T )=fold(I，τ)T ×1S1×2S2…×NSN，Hτ(W )=fold(I，τ)W ×1S1×2S2…×NSN，得到折叠后的张量T，坐标张量W，ρ，p，信号失真率SDR 和停止阈值υ；

（7）t 从0 到max iter 重复执行步骤①～④。

①r 从1 到R 执行步骤a）～e）

图1 基于多向延迟嵌入的平滑CP 分解算法过程示意图Fig.1 Process diagram of smooth CP decomposition algorithm based on multi-direction delay embedding

步骤。

a）R=R+1；

③t=t+1；

④如果μt≤ε，或者t=max iter，跳出本层循环。

3 实验与分析

脑胶质瘤是一种恶性肿瘤，具有易复发、存活率低的特点［11］。世界卫生组织根据肿瘤病理的恶性程度，将胶质瘤划分成四级，其中Ⅰ～Ⅱ级为低级别胶质瘤（LGG），Ⅲ～Ⅳ级为高级别胶质瘤（HGG）［12］。中国脑胶质瘤5 年病死率在全身肿瘤中仅次于胰腺癌和肺癌［13］，本实验采用的是2017 年MICCAI BraTS 数据集［14-17］，共285 个病人的磁共振图像，包括75 例低级别胶质瘤和210 例高级别胶质瘤。每个病人的MRI 影像数据包括4 种模态：T1，T1ce，T2 和Flair，如图2 所示。

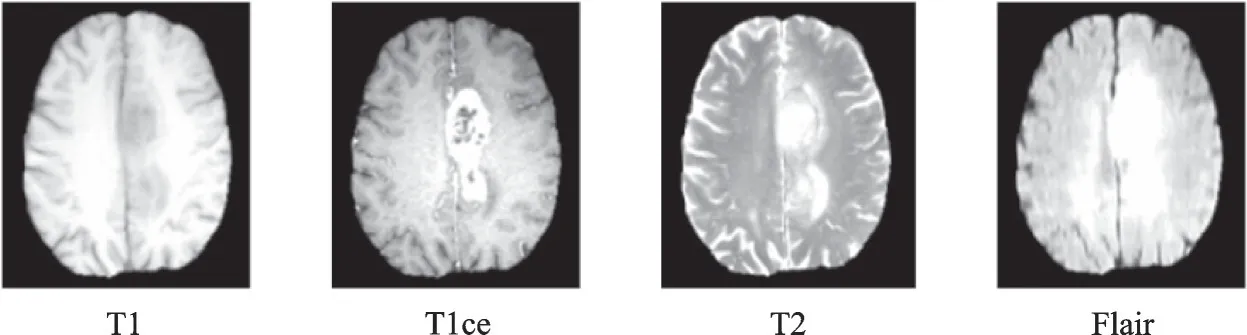
图2 BraTS2017 数据集Fig.2 BraTS2017 dataset

分别对每一种模态提取一阶统计特征和二阶纹理特征。一阶统计特征包括体积、坚固性和偏心度；二阶纹理特征包括3 种全局纹理特征以及从灰度共生矩阵（Gray-level co-occurrence matrix，GLCM）、灰度游程矩阵（Gray-level run-length matrix，GLRLM）、灰度区域大小矩阵（Gray level size zone matrix，GLSZM）和邻域灰度差分矩阵（Neighborhood gray-tone difference matrix，NGTDM）中分别提取的9、13、13、5 个特征，即每个模态提取46 个特征，最后4 个模态一共得到184 个特征。

每个模态随机挑选出20%的样本，将挑选出的样本的对应模态特征做缺失处理，得到不完整的矩阵T。矩阵T 的数据形式如图3 所示，阴影部分为缺失的数据。行数据是每个病人的特征数据，每列是对应的特征，A1～A46 是由模态T1 提取的46 个特征，B1～B46 是模态T1ce 提取的特征，以此类推。

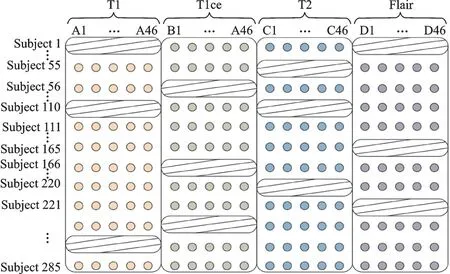
图3 特征矩阵示意图Fig.3 Schematic diagram of characteristic matrix

首先使用数据补全算法将不完整的特征数据补全，之后使用线性核的支持向量机进行高级别胶质瘤和低级别胶质瘤的二分类任务，最后使用平均分类准确率评估各算法性能，实验流程如图4 所示。基准方法包括：补零法、邻近算法、奇异值分解算法［18］、期望最大化算法、低秩矩阵补全［19］、低秩张量补全［20］和基于多向延迟嵌入的Tucker 分解算法。实验采取留出法，每次都按照4∶1 随机选取训练集和测试集的病人，重复进行高级别胶质瘤和低级别胶质瘤的分类实验，共重复1 000 次，计算平均分类准确率，结果如表1 所示。

图4 实验流程图Fig.4 Experimental flow chart

表1 实验结果Table 1 Experimental results

由表1 可知：经过本文提出的基于多向延迟嵌入的平滑张量补全算法补全的矩阵，其分类效果相比传统算法要好，准确率达到91.31%；相比于原算法——基于多向延迟嵌入的Tucker 分解算法也有一定程度上的提升，分类精度提升了1.44%。实验结果表明，改进算法减轻了由于缺失模态问题造成的特征丢失，使得分类准确率有了进一步提升。

4 结束语

本文在多向延迟嵌入Tucker 分解算法的基础上，提出了一种基于多向延迟嵌入的平滑张量补全算法，主要是将数据经过多向延迟嵌入操作后进行平滑张量CP 分解，最后进行多向延迟嵌入的逆向过程，得到补全的数据。实验结果表明，改进后的算法弥补了原算法Tucker 分解的不足，增强了算法的降噪能力，具有更好的补齐效果和鲁棒性。算法也依然存在计算复杂度较高等不足之处，将在接下来的研究中进一步改善。