进口探针支杆诱发压气机转子叶片振动的流固耦合研究
2021-02-03刘氦旭杨荣菲向宏辉高杰
刘氦旭,杨荣菲,向宏辉,高杰
(1. 南京航空航天大学 能源与动力学院,江苏 南京 210016;2. 中国航发四川燃气涡轮研究院,四川 绵阳 621000)
0 引言
浸入式探针的存在会在原本干净的流场中产生扰动源,造成堵塞影响流场结构,进而影响叶轮机械气动性能,或因进口探针与压气机之间相互作用剧烈而导致压气机转子进口气流角大幅值变化[1]使压气机的失速裕度大幅降低。为了弱化探针对压气机性能的影响,叶型探针技术被提出。将探头安装在叶片前缘以扣除探针支杆堵塞影响,但探头的存在改变了叶片前缘几何形状,并严重改变了当前叶片通道流场结构[2]。采用更细的探针支杆,如尺寸较长的长条型探针支杆[3]、尺寸略微减小的尾缘修型支杆[4]被提出,以削弱探针支杆尾迹,进而减少支杆与压气机相互作用。TERUNA C等[5]数值研究发现探针脱落涡冲击叶片会造成非常大的压力波动,但并没深入研究对叶片振动的影响。由此可见国内外研究者基本集中于研究探针对压气机气动性能或对叶片通道噪声的影响,而忽略了探针对叶片振动的影响。在某次压气机远离失速边界的试验过程中发现,某探针支杆的引入导致压气机第一级转子叶片动应力超限。这个现象的发现意味着探针支杆引起下游压气机转子振动问题并不能被完全忽略。
理论上来讲,探针诱导叶片应力超限是流固耦合问题,越来愈多的研究者开始通过流固耦合[6]数值计算方法对振动问题进行研究,并结合文献[7]指出相位延迟技术能够大大提高计算叶片振动的速度,并能够有效预测叶片气动阻尼等振动特性。因此本文将采用相位延迟流固耦合数值计算方法研究有/无探针支杆影响下压气机转子叶片振动特征。
1 研究对象及数值方法
1.1 研究对象
压气机流道示意图见图1,共有36个IGV进口导叶, 62个S0静子叶片,87个R1转子叶片。一支直径为10mm圆柱型探针安装在截面1a-1a上,其距离R1叶中前缘3.5倍轴向弦长、与展向夹角6.217°。此时支杆叶中截面相较S0周向位置、轴向位置以及进气角度如图2所示。
下文针对探针支杆诱发压气机振动失效工况开展流固耦合数值计算研究,并与无探针方案进行对比,探讨转子叶片动应力超限机理。

图1 压气机的子午流面及相关数据

图2 叶中截面测试探针相对S0的周向位置
1.2 模型简化及网格划分
1)模型简化
由于全周数值模拟的总网格量将上亿,由于当前计算资源限制,对图1中的真实模型进行简化。由文献[8]可知,当叶片振动位移呈收敛趋势,采用单通道计算方法可预测叶片振动特性,故在下文无探针模型中采用单通道。
针对带探针支杆的压气机模型,探针支杆和S0可以合并为一个静子域,与压气机转子非定常作用问题仍可以采用相位延迟方法预测叶片振动。因此,调整探针和S0的数目为10和60,约化为6/1模型见图3。由文献[9]结果可知本文均布的10支探针合理,能够避免相邻探针之间产生干扰。此外S0叶片数降低仅使负荷增加3%,对压气机流场结构不会产生太大影响。由于探针支杆尾迹影响3~4个转子通道,故转子计算域选择4个转子通道。最终带支杆的压气机计算模型见图3,图中沿转子旋转方向对转子叶片标号为r1、r2、r3、r4。

图3 流体计算域
2)网格划分
流体域网格由Autogrid5自动生成,壁面第一层网格高度为0.003mm,y+为1.01。各叶排网格量及端壁间隙量见表1,图4给出了叶中截面网格及支杆、转子间隙内网格。

表1 各叶排网格量及间隙特征

图4 叶中截面网格示意图及局部示意图
流固耦合计算时仅考虑转子振动,使用ABAQUS软件对转子固体域划分Tet型有限元网格,沿展向、流向分别布置30、50个节点,并加密前尾缘附近节点以保证前缘尾缘的几何不失真,总网格量为68480,如图5所示。

图5 转子Tet型有限元网格
1.3 网格无关性验证
1)流体网格
计算得到表2中不同网格量下S0、R1叶片50%叶高截面静压见图6,可以发现,三种网格计算得到的叶片静压曲线完全重合,故从缩短计算时间考虑,本文流体计算网格选择mesh1。

表2 不同网格量

图6 S0/R1叶片表面压力延流向分布
2)固体网格
转子叶片材料为通用铝合金,密度2770kg/m3,弹性模量7.1×1010Pa,泊松比0.33。使用ABAQUS对4种不同网格量的有限元模型在转速4600r/min载荷下进行瞬态动力学计算,时间步长0.01s,计算时长1s。对比图5中蓝点位置的应力见表3(因本刊为黑白印刷,有疑问之处可咨询作者)。从表3可以看出,当固体网格节点超过6.8万后,应力预估值收敛,考虑采用FE_4网格进行振动计算所需时间是FE_3模型的十几倍,最终选择FE_3网格作为固体域计算网格。

表3 不同网格量下转子叶片表面振动应力
1.4 流固耦合数值方法
利用MPCCI软件平台将Numeca软件计算的流动结果与ABAQUS软件计算的固体振动结果进行流固耦合面的信息交互,以实现压气机的流固耦合计算,计算流程见图7。
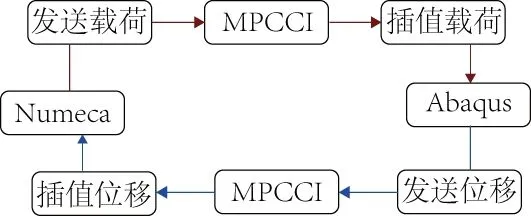
图7 耦合平台流程图
Numeca采用SA湍流模型,并采用双精度求解,进出口边界条件按照试验给定,进口给定总温、总压、进气角,出口给定反压,固壁绝热无滑移,侧向周期性边界及转静交界面使用相位延迟边界,同时选择IDW(inverse distance weighting)多层动网格技术模拟转子叶片运动。流体域计算时间步长定义为一个转子叶片通道计算20步,对应的时间步长为tCFD=7.496 251 87×10-6s。
由于Abaqus指定的时间精度最多为5位,Numeca双精度计算方法时间精度大于5位,在时间尺度上两个软件难以完全一致,因此设定ABAQUS计算时间步长为7.5×10-6s,流固耦合计算过程中采用非匹配时间步长耦合方法。
ABAQUS计算时叶片底部自由度均设置为0,施加4600r/min预应力载荷,并在每个转子叶片的吸力面90%叶高、距前缘20%轴向弦长处监控叶片位移以及动应力,监测点位置见图5中的灰点标识。
2 流固耦合计算结果分析
2.1 固体域振动特性分析
图8给出了探针支杆影响下计算域中4个转子叶片监测点周向位移以及动应力随时间变化情况,可以看出,r1、r2叶尖位移逐渐增加,r3、r4叶尖位移逐渐衰减,表明r1、r2叶片可能会出现振动失效问题,r3、r4叶片处于振动安全状态,其中r2叶片振动位移增加最大,对应的r2叶片是探针支杆尾迹影响下最容易出现振动失效的叶片。除此之外,图8(b)中r1、r2、r3叶片的动应力时变曲线呈发散趋势,r4叶片的动应力时变曲线呈衰减趋势,且r2的动应力增加幅值最大,与振动位移曲线获得的结果一致。
图9给出了无探针时转子叶片监测点振动特征,可以看出,叶片的位移以及动应力随时间均逐渐衰减,说明叶片不会发生振动失效。
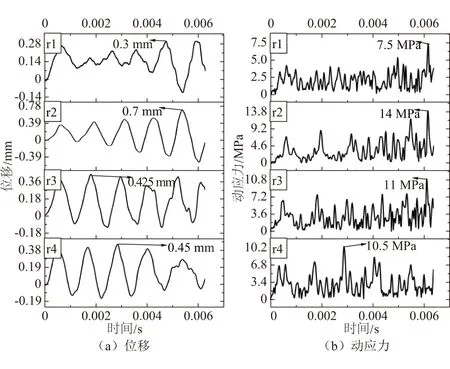
图8 有探针时叶片沿y方向的位移、动应力
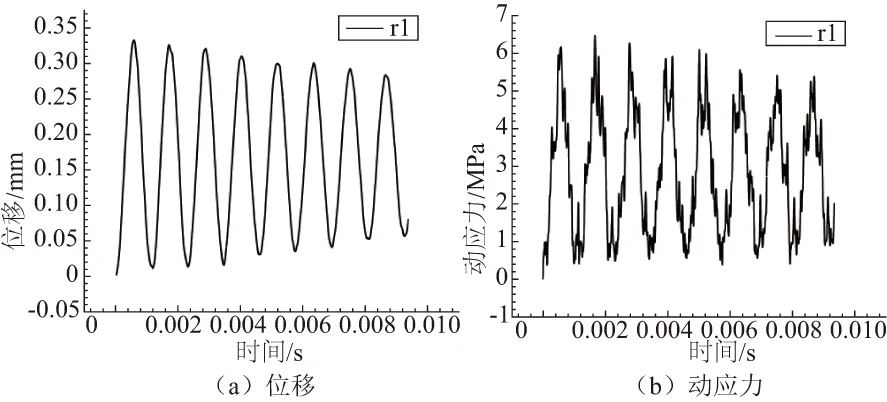
图9 无探针时叶片沿y方向的位移、动应力
图10、图11给出了转子振动位移最大时刻的吸力面瞬时动应力和位移分布云图,其中图10为探针支杆影响下r2叶片振动时刻t=0.005 6s, 图11为无探针支杆影响工况。对比可以发现,有/无探针支杆时叶片吸力面的应力、位移分布基本相同,仅幅值不同,在探针支杆影响下,转子吸力面应变、位移都近似无探针情况的2倍,说明探针支杆的存在影响整个叶片的振动特征。
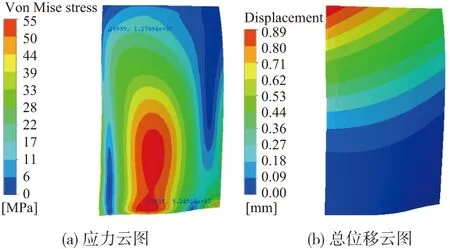
图10 带探针时r2应力和总位移云图(t=0.005 6 s)

图11 无探针时叶片应力和总位移云图(t=0.008 7s)
2.2 流体域特性分析
为了获得探针支杆引起转子叶片振动失效的流动机理,图12、图13分别给出了有/无探针支杆影响下转子叶片表面瞬时静压分布云图。可以看出,有探针支杆时,r2叶片的前缘叶尖的静压大于其他叶片,并远大于无探针时叶片相同位置点的静压,表明支杆尾迹改变了转子叶片表面静压分布。
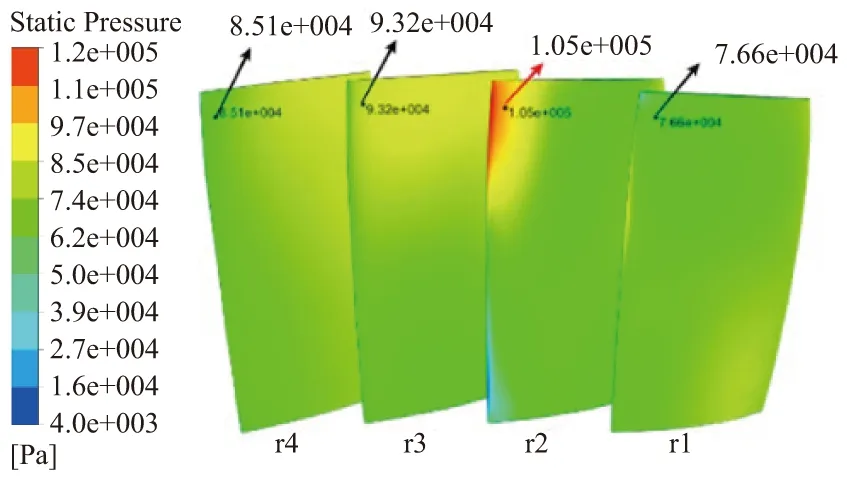
图12 有探针时叶片表面瞬时静压云图(t=0.0056s)

图13 无探针时叶片表面瞬时静压云图(t=0.0087s)
图14进一步给出了有探针时转子叶片90%叶高处的瞬时静压分布,发现不同叶片前缘负荷不同,r1、r2叶片前缘附近都是吸力面静压大于压力面静压,对应于叶片处于负攻角状态,同时叶片后半部分都是压力面静压大于吸力面静压,这类压力分布最终造成叶片扭转;而r3、r4叶片整个弦长都是压力面静压大于吸力面,对应于叶片处于正攻角状态,叶片出现弯曲变形。由此可以推断,支杆尾迹引起叶片表面静压大幅变化,使得转子叶片振动形式由弯曲到扭转的周期性变化,是造成转子振动应力失效的原因。
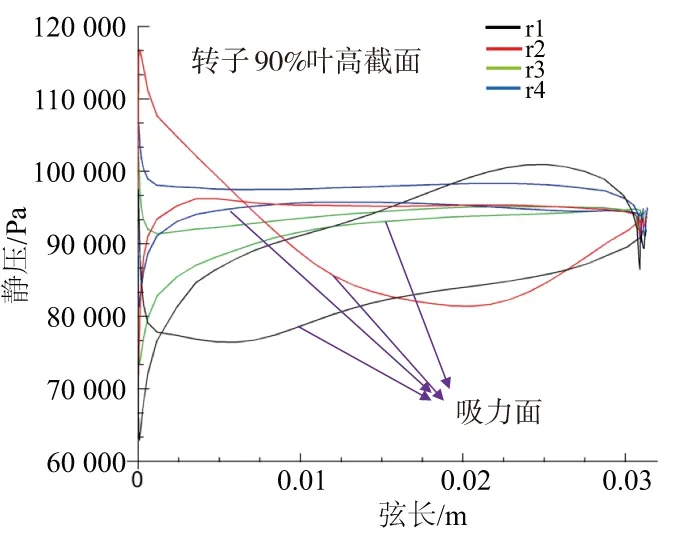
图14 转子90%叶高处叶片表面的瞬时静压分布(t=0.005 6 s)
3 结语
对比上述有探针和无探针的计算结果,发现如下结论:
1)无探针时叶片振动呈收敛状态,有探针时各叶片的振动形式各不相同,其中r2叶片振动位移及应变时间曲线发散,造成探针支杆影响下叶片高周疲劳失效。
2)探针支杆尾迹引起压气机转子叶片前缘负荷大幅变化,转子叶片振动形式从弯曲变为扭转,是叶片失效的主要原因。
