复合材料层合板疲劳载荷下固有频率衰减预测模型

张善之，温卫东，张宏建

(南京航空航天大学 航空发动机热环境与热结构工业和信息化部重点实验室，江苏 南京 210016)

0 引言

复合材料与传统的金属材料相比，因其质量轻、比强度高、比刚度大及可设计性强等优势，已被军事及民用等行业广泛采用[1]。随着应用范围的扩大，复合材料构件的疲劳问题日益受到重视，如何监测复合材料剩余疲劳寿命变得尤为重要。

目前国内外对树脂基复合材料的剩余寿命模型进行了很多研究。徐颖[2]基于等效损伤原理，将无损单层板理论引入层合结构的材料性能渐降模型中，建立了包含基体开裂、基纤剪切、分层、纤维断裂等复合材料层合板主要失效模式的疲劳寿命预测方法。王丹勇[3]基于Hashin失效准则，提出了以纤维断裂损伤形式控制复合材料结构的最终失效准则，且考虑了4种损伤基本类型相互关联作用的材料性能突降。上述研究均能有效预测层合板的剩余疲劳寿命，但在实际工程问题中，在不损伤材料结构的情况下，测量材料当前所处的寿命是比较困难的。

目前发展较为成熟的损伤检测技术是基于加速度测量的振动分析理论，且可以分为以下3类：固有频率法、振型法、其他模态参数法。早在1978年，ADAMS R D等[4]就提出可通过对结构两个不同时段的固有频率进行对比，从而检测损伤。但目前基于模态分析的疲劳剩余寿命预测研究却鲜有报道。本文基于对称层合板模型与Hashin失效准则，应用逐渐损伤模型，编写APDL参数化程序，针对T300/970复合材料层合板拉-拉疲劳载荷下的寿命循环比与固有频率的关系展开有限元数值模拟，验证了二者之间存在一定的数值关系。

1 复合材料层合板逐渐损伤模型

1.1 层合板损伤判据

复合材料层合板在疲劳过程中伴随以下几种破坏损伤：纤维拉伸断裂、纤维压缩断裂、基纤剪切、基体开裂、基体挤压及分层损伤。本文基于Hashin静态准则，结合徐颖[2]所提出的疲劳失效准则，提出以上6种损伤的失效判据如下：

纤维拉伸断裂判据：

(1)

纤维压缩断裂判据：

(2)

基纤剪切判据：

(3)

基体开裂判据：

(4)

基体挤压判据：

(5)

分层判据：

(6)

其中σxx、σyy、σzz、σxy、σyz、σxz分别为层合板主轴方向应力及面内切应力；X(n,k,σ)、Y(n,k,σ)、Z(n,k,σ)代表各方向在疲劳载荷作用下的剩余强度，其下标T为拉伸，C为压缩；同理Sxy(n,k,σ)、Syz(n,k,σ)、Sxz(n,k,σ)表示层合板面内的剪切剩余强度，n、k、σ分别代表循环数、载荷比、应力水平。

1.2 层合板性能退化方式

复合材料层合板性能退化的方式一般有两种：由于结构损伤导致性能突降和随疲劳循环次数增加而产生的性能渐降。前者只在满足上述6种失效判据时出现，后者满足渐降准则存在于全疲劳循环中。

本文假定满足失效判据时性能按以下方式退化：

1) 纤维拉伸及纤维压缩损伤：Exx、Eyy、Ezz、Gxy、Gyz、Gxz、υxy、υyz、υxz全性能退化为初始值的0.07；

2) 基纤剪切损伤：Gxy、υxy退化为0；

3) 基体开裂及基体挤压损伤：Eyy、Gxy、Gyz、υxy、υyz退化为初始值的0.2；

4) 分层损伤：Ezz、Gxz、Gyz、υxy、υyz退化为0。

渐降准则参考SHOKRIEH M M等[5- 6]人提出的幂函数渐降模型，如下所示：

S(n,k,σ)=

(7)

E(n,k,σ)=

(8)

式中：S0、E0分别为复合材料单向板的初始强度与初始刚度；εf为材料破坏时应变；Nf为疲劳总寿命；α、β、λ、γ为拟合参数，参考文献[2]中拟合数据，如表1所示。

本文参考BEHESHTY M H[7]提出的等寿命模型求得Nf，如下所示：

(9)

式中：a、m、c可由拉伸与压缩强度、载荷幅值、平均疲劳载荷求得；f根据经验取1.06；A、B为拟合参数，参考文献[2]中拟合数据，如表2所示。

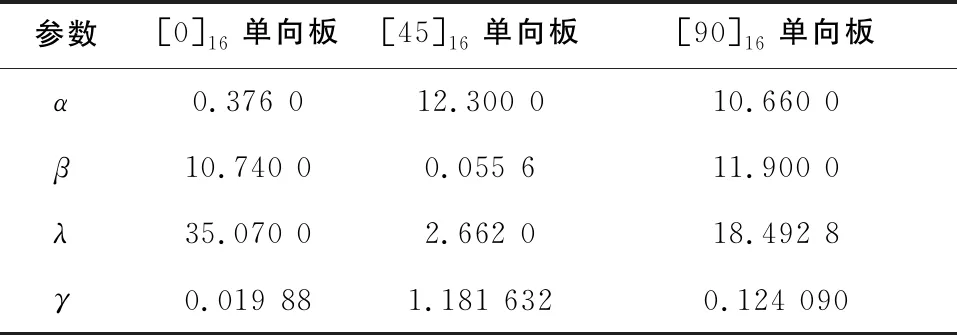
表1 单向板剩余刚度/强度模型参数

表2 单向板等寿命模型参数

2 损伤对层合板固有频率的影响

复合材料构件在其使用过程中常伴随着疲劳损伤，而损伤带来的则是其结构刚度的衰减，从而导致固有频率降低。本节结合层合板本构模型及摄动理论，将固有频率降低率量化。

对称铺层层合板模型如下：

(10)

式中：εx、εy、εxy为各方向应变分量；kx、ky、kxy为层合板中性面的曲率分量；Aij为拉伸刚度系数；Bij为耦合刚度系数，对于堆成铺层层合板为0；Dij为弯曲刚度系数。上述刚度系数与各方向弹性模量、泊松比之间具有一定的数量关系。

层合板合内力矩及动平衡方程公式如下：

(12)

(13)

将合内力矩公式代入动平衡方程可得到复合材料层合板的自由振动平衡方程：

(14)

边界条件选取自由-自由边界条件，结合层合板振动理论可得出自由振动的精确解如下式：

(15)

由上式可见，固有频率精确解与弯曲刚度系数相关密切，而疲劳损伤的发生会对刚度产生影响，进而改变弯曲刚度系数，导致固有频率发生变化。

3 固有频率衰减模型拟合及验证

本文采用商用有限元软件ANSYS进行有限元分析，通过其内嵌APDL语言进行建模仿真编程，流程图如图1所示。

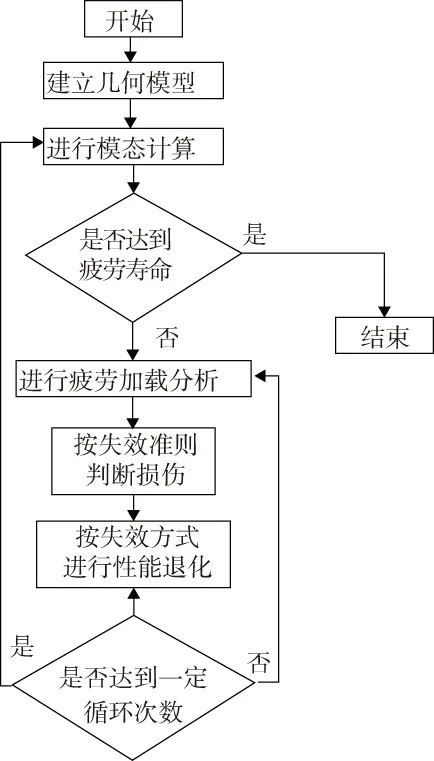
图1 APDL流程图

本文选用T300/970树脂基复合材料为仿真材料，层合板模型图如图2所示，各层铺层方向为[45/0/-45/0/45/0/-45/90]s对称铺层，共计16层，单层厚度0.155mm，总厚度约2.5mm，形状为工字梁，总长度130mm，总宽度30mm，中间段长46mm，宽10mm，连接处为圆弧，半径为30mm。材料性能参数参考文献[8]，如表3所示。

图2 材料模型示意图

表3 T300/970复合材料性能结构参数

3.1 固有频率模拟分析

按文中表1参数在ANSYS仿真软件中建立试件的几何模型，并利用有限元法对其进行固有频率预测，边界条件为自由-自由，预测结果与文献[8]中的试验数据对比如图3所示。

图3 固有频率预测值与试验值对比

对比发现，预测的固有频率值与实际试验结果十分相近，且略大于试验值。原因是试验中的振动时响应信号由加速度传感器接收，而加速度传感器的附加质量会影响实际试验的频率值，使之减小。由图3所示与试验数据的对比，证明了模态预测的可靠性。

3.2 固有频率衰减模型拟合

疲劳循环模拟中仍使用上述几何模型，对其在长度方向上施加循环载荷边界条件。参考文献[8]给出该种尺寸材料平均拉伸静强度为723MPa。取载荷比为0.1，应力水平为75%，最大加载应力为542.25MPa。实际加载过程采用正弦波形如图4所示。

对每次循环后的各个单元读取各方向应力并按失效判据进行损伤判断，如果出现损伤则单元性能按照退化准则进行退化，对于未出现损伤的单元性能按照幂函数渐降模型随循环次数进行渐降。取疲劳循环过程中各寿命阶段的几何模型进行模态预测，并选取自由状态进行预测其对应的循环比下固有频率值。

图4 疲劳循环载荷谱

图5为5种不同循环比时数值模拟求得的固有频率下降率与所对应疲劳循环比之间关系。由图中可以看出固有频率下降率和疲劳循环载荷比之间明显存在一定的函数关系。本文选用对数函数模型，选取第二阶模态通过遗传算法对其进行最优化拟合。函数模型为：

g=pln(qr+1)

(16)

式中：g为固有频率下降率；r为疲劳循环比。g、r表达式如下：

(17)

(18)

式中p、q分别为拟合参数，由材料、类型、尺寸、应力水平和选取的模态阶数等参数所决定。按上述模型拟合得出的第二阶模态预测模型如下式所示：

g=0.10478ln(37.92976r+1)

(19)

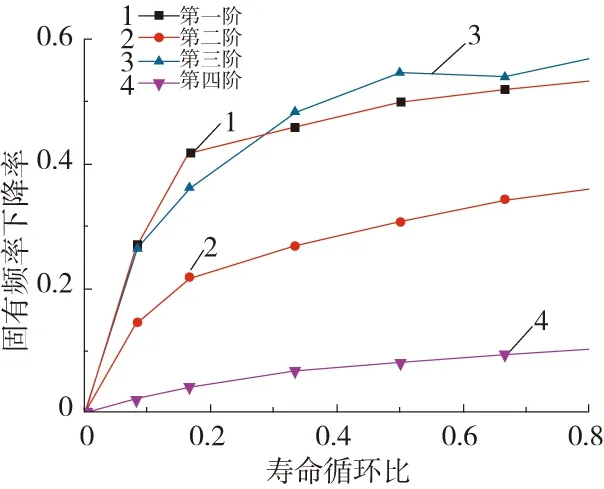
图5 前4阶固有频率下降率变化图

3.3 衰减模型验证

将上述拟合模型与文献[8]中的试验数据进行对比，结果如图6所示。由图可见拟合模型曲线与试验数据曲线吻合度非常高。但是在疲劳循环比0.4～0.8的过程中存在一定的误差，其主要原因为层合板疲劳进行过程中总伴随着边界效应[9]，导致复合材料的自由端容易较早发生分层损伤，从而对复合材料的边界刚度有加强作用，导致固有频率下降率减小，使数值模拟结果与试验结果产生一定的误差。因此本文所参考的损伤后刚度突降模型有待进一步改进，应考虑更多的边界效应影响因子，有助于更好地反映实际试验中的固有频率下降率。

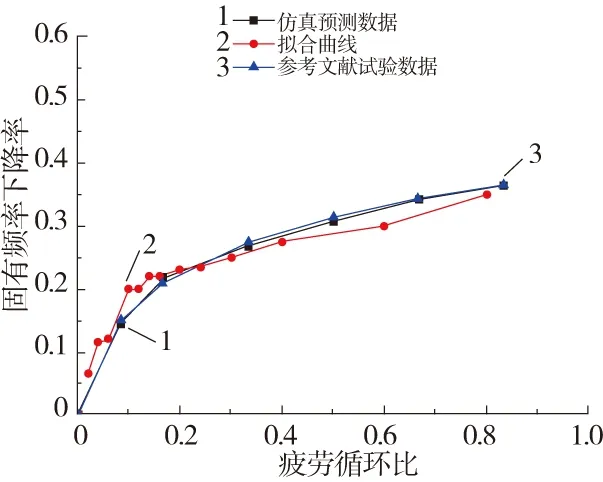
图6 T300纤维复合材料层合板数值模拟结果

4 结语

本文基于层合板逐渐损伤模型，采用率相关的硬化方程，编制了本构模型的APDL参数化程序，利用ANSYS软件开展了T300/970树脂基复合材料层合板在0.1载荷比、75%应力水平下的固有频率下降率数值模拟研究，并建立了符合疲劳循环比与固有频率下降率关系的对数函数模型。结果表明：该模型具有一定的可靠性，有效利用拟合模型，对实际工程中通过固有频率下降率预测剩余疲劳寿命有很大的实际意义。