基于非线性模型预测的可变截面涡轮增压器控制

张卫波，梁昆，朱清

(福州大学 机械工程及自动化学院，福建 福州 350116)

0 引言

增压柴油机在客车、货车、轿车等车型上的应用越来越广泛。在稳态工况下，相比于普通柴油机，涡轮增压器可以提高发动机的动力性、排放性及经济性等。而实际运行工况总是多变的，发动机性能需要实时改变，常规涡轮增压柴油机在多变的运行工况下，存在严重涡轮迟滞现象，变化的供油量与进气量无法同步变化，影响柴油机的输出性能[1-2]。可变截面涡轮增压器(VGT)是解决以上问题的有效手段，可根据实际工况改变VGT开度，从而改变柴油机运行工况。

对于VGT的控制，国内外学者主要采用PID控制。昆明理工大学提出前馈控制与自适应PIDGT开度[3]。北京理工大学通过PID算法的闭环目标升压反馈，提高了发动机的容积效率[4]。HONG S等研究人员提出了一种以SIMC为基础的乘用车柴油机升压控制器增益调度策略，用于满足VGT的非线性特性[5]。而单独使用PID控制，并不能对增压柴油机参数之间的非线性关系进行处理，所以本文对非线性关系采用非线性模型预测，同时利用量子粒子群算法对VGT开度寻优。

1 基于BPNN的预测模型

对于预测模型，常见的预测方法可以分为热力学建模和数据统计两种方式[6]。热力学建模方法是对发动机物理和化学过程的简化和假设，同时考虑发动机运行工况，模型需要调整和校准，因此这不可避免地导致其在校准区域外的预测误差。数据统计方法主要针对输入变量和输出之间的线性关系，但在处理非线性问题时，存在预测不灵活且缺乏准确性。这两种方法都不适合于解决非线性关系，而BP神经网络具有并行计算和以任意精度逼近非线性系统的能力[7-8]。为此本文采用BPNN建立预测模型。

1.1 预测模型的建立

预测模型是根据增压柴油机数据，准确预测下一时刻发动机的进气量与排气压力。在发动机中，空气通过进气管进入气缸，并且随着发动机转速的变化，单位时间内进入的空气量随之改变。因此，进气流量与发动机的转速息息相关，同时，下一时刻的进气流量与之前的进气流量也有关系。对此，本文选用前面时刻的发动机转速、VGT开度、排气压力和进气流量来预测下一时刻的进气流量。即模型输入量表示为：

x(k)=[Pex(k),VGT(k),Neg(k),ma(k)]T

(1)

式中：Pex(k)、VGT(k)、Neg(k)、ma(k)分别为k时刻下的排气压力、VGT开度、发动机转速和进气流量。同时下一时刻的进气流量和排气压力作为输出量表示为：

(2)

根据式(1)和式(2)的输入量和输出量，选用3层神经网络结构构造预测模型，结构如图1所示。神经网络的输入层、隐含层和输出层神经元个数分别设为I、H和Q，隐含层输入表示为：

Iinput=w1x(k)+b1

(3)

Iinput=[Iinput1,…,Iinputa,…,IinputH]T,a=1,2,…,H

(4)

其中：w1∈RH×I是输入层和隐含层之间的权值矩阵；b1∈RH×I是隐含层的阈值矩阵；Iinput∈RH×1是隐含层的输入量矩阵，隐含层的输入量传递至激活函数Sigmoid，得到隐含层的输出量，输出量表示为：

(5)

Ooutput=[Ooutput1,…,Ooutputa,…,OoutputH]T

a=1,2,…,H

(6)

其中：Ooutputa和Iinputa分别是隐含层第a个神经元的输出量和输入量；Ooutput∈RH×1是隐含层输出量矩阵。而预测模型的输出量表示为：

(7)

其中：w2∈RO×H是隐含层和输出层之间的权值矩阵；b2∈RO×1是输出层的阈值矩阵。

本文通过AMESim商业软件建立的六缸增压柴油机，再调整发动机转速、喷油脉宽和VGT开度，运行模型从而得到训练样本，见图2和图3。另外，BP神经网络需要在训练之前对权值和阈值进行初始化，而不同的初始权值和阈值会导致训练出来的网络的预测效果不同[9]。因此为了寻找最优初始值从而提高网络的预测精度，本文采用遗传算法(GA)对神经网络初始值进行寻优，再利用BP神经网络对预测模型进行权值优化，最终得到进气量预测模型。同时，神经网络中的隐含层个数对预测模型产生影响，本文通过多次试验，对比不同隐含层神经元个数对模型的误差影响，将隐含层神经元个数设置为40。

图1 BP预测模型结构

图2 训练输入数据

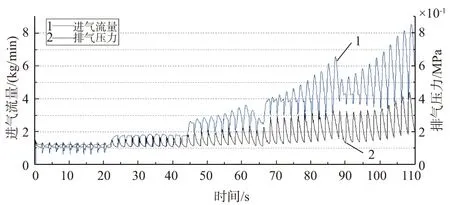
图3 训练输出数据

1.2 进气量预测模型验证

为了验证进气量预测模型的预测能力，本文在相同输入量下，对比进气流量的预测值与实际值。对于输入量使用Gaussian信号，设置VGT均值为0.5，方差为0.04，周期为0.5s，转速设置为均值2500r/min，方差为1000，周期为0.5s，喷油脉宽设置为均值1.3ms，方差为0.06，周期为0.5s。预测模型的预测值和实际值对比结果见图4和图5。本文对于预测模型结果的误差采用3种评价标准，见表1。从表1可以看出，进气流量和排气压力的均方误差低于0.2，平均绝对误差在0.1左右，而进气流量的平均绝对百分比误差在2%左右，排气压力的平均绝对百分比误差为4%左右。从这些数据可以看出，该预测模型可以准确地预测出增压柴油机下一时刻的进气流量和排气压力。

图4 排气压力真实值与预测值对比图

图5 进气流量真实值与预测值对比图

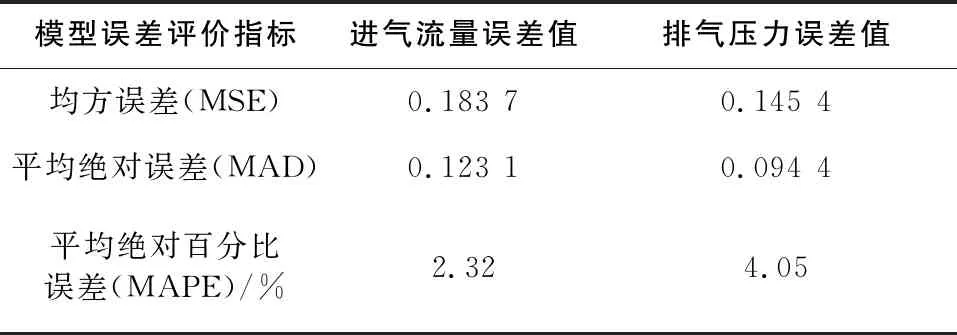
表1 模型误差评价指标

2 量子粒子群算法寻优

2.1 量子粒子群算法寻优

普通PSO算法出现粒子快速汇聚在局部最优解处，同时导致粒子的过早收敛和种群数量过快减少。另外，普通PSO算法需要设置惯性因子和加速因子参数，需修改的参数数量较多，而量子粒子群算法(QPSO)可以有效解决这两个问题[10]。在QPSO算法[11-12]中，其舍弃了粒子的运动方向属性，粒子位置的更新与之前的位置无关，增强了粒子的随机性。

同时，由于考虑到VGT的开度不仅仅影响下一时刻的进气流量，同时对未来时刻的进气流量皆有影响。另外，在控制VGT时，不宜将VGT开度大幅度变化，大幅度变化会导致柴油机进气流量的波动，从而出现柴油机输出转矩波动。因此，本文将进气流量变化和VGT开度变化都考虑在内，算法的适应度函数表现如下：

(8)

n=1,…,Np

(9)

Q=diag(qk+1,qk+2,…,qk+n,…,qk+Np),n=1,2,…,Np

(10)

对于其中VGT粒子变化，本文采用QPSO算法，其粒子位置变化如下：

P(t)=θ(t)pbesti(t)+[1-θ(t)]gbest(t)

(11)

(12)

其中：θ是0～1的随机数；t为迭代次数；为0～1的随机数；α为创新参数，该参数是QPSO唯一需要修改的参数。另外，公式(12)中，该式取加号与减号的概率一样，均为50%。

对于进气流量的参考值，本文根据实时的燃油消耗量和转速，计算得出实际需要的进气流量作为期望进气流量。增压柴油机工作时，过量空气系数一般在1.5～2.4之间。通过多次试验，本款柴油机过量空气系数在1.7左右时，其输出转矩大于其他过量空气系数下的输出转矩。因此，本文选取1.7为本款柴油机的最优过量空气系数。

为了对比QPSO和SPSO的优化能力，本文随机选取一个增压柴油机工况，采用公式(8)作为适应度函数，比较SPSO和QPSO优化过程。同时，试验分别在预测时域为5和10进行。在预测时域为5的试验中，粒子种群设置为10，迭代次数设置为10；在预测时域为10的试验中，粒子种群取15，迭代次数取15，试验结果见图6和图7。

图6 预测时域为5的迭代结果

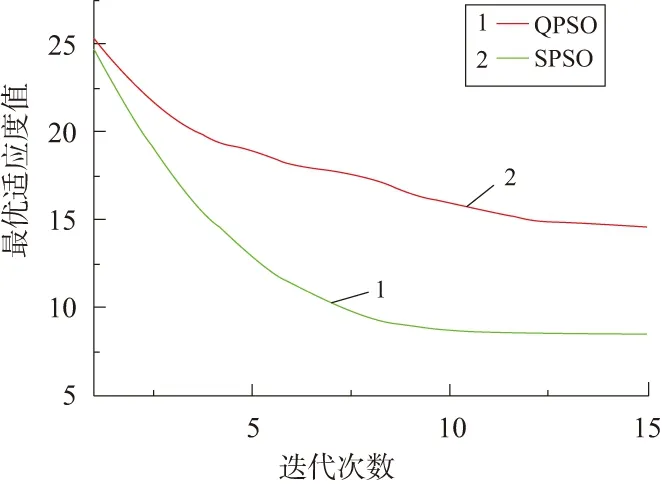
图7 预测时域为10的迭代结果

2.2 非线性模型预测控制算法

本文利用BP神经网络构建预测模型，预测出未来时刻增压柴油机的进气流量和排气压力。通过比较各个粒子VGT开度下的适应度值，寻找出最优VGT开度。再利用最优的VGT开度控制增压柴油机，使其达到过量空气系数期望值和转矩期望值。整体控制流程图如图8所示。首先，利用BP预测模型预测出预测时域Np下的进气流量，再与期望进气流量比较，获得两者之间的误差以及VGT开度的差值构成目标函数。然后，求解各个粒子的目标函数值，利用QPSO算法迭代对VGT开度寻优，得到最优的VGT开度，使增压柴油机平稳达到转矩期望值。

图8 非线性模型预测控制流程图

3 VGT仿真实验

本文使用AMESim和MATLAB/Simulink进行联合仿真，通过AMESim软件生成S函数，添加至Simulink模块中，实现AMESim进行柴油机仿真，Simulink进行控制输出[13]。本文每0.1s对柴油机数据进行采集，并对VGT开度进行控制，同时鉴于预测模型对预测进气流量存在误差，本文在VGT开度寻优前，先对下一时刻进气流量预测，若其与期望流量相差在5%以内，将不调节VGT开度，保持原有VGT开度，避免VGT的过度调控。接下来的仿真试验中，本文将预测时域取为5，迭代次数和种群数量取10，权值p取为1，权值Q取值如下：

Q=diag(10,10,10,10,10)

(13)

3.1 瞬态响应仿真

本次仿真主要是模拟在柴油机工作时，负载瞬间变化，对比PID算法和BP-QPSO算法的适应能力。本文使柴油机转速调至1500r/min，在5s末，燃油消耗量由0.106kg/min阶跃为0.169kg/min，之后燃油消耗量维持在0.169kg/min。在5s后分别使用PID算法和BP-QPSO算法控制VGT开度，运行结果见图9和图10。从图中可以看出，两种算法控制VGT开度都将增压柴油机的过量空气系数提高至1.7，使用BP-QPSO算法对VGT控制，使柴油机运行更加平稳，而PID需要经过一段时间才能使转矩平稳。由于PID算法使VGT开度出现大幅度减少，导致涡轮迟滞加重，柴油机运行不平稳。因此，BP-QPSO算法在瞬态响应工况下，相比于PID算法可以使增压柴油机运行更加平稳。

图9 转矩阶跃响应变化

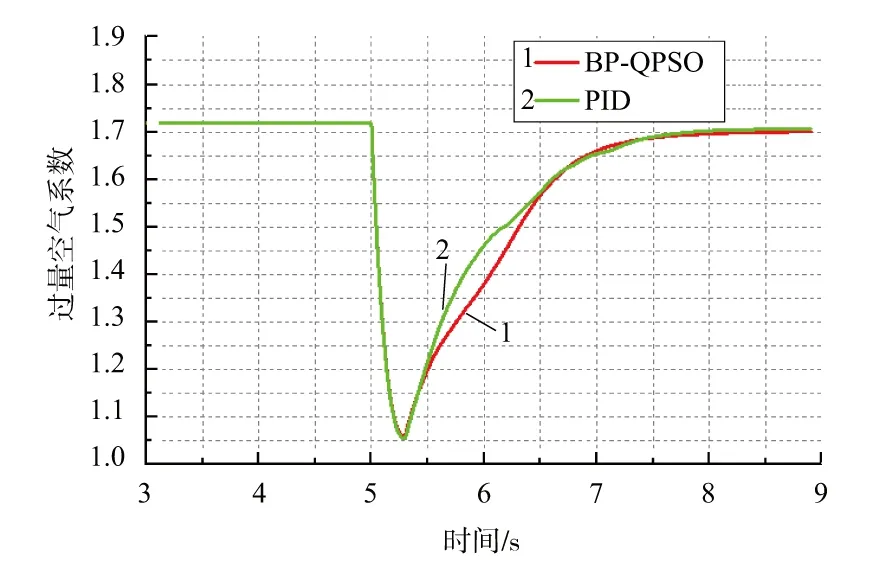
图10 增压柴油机过量空气系数变化

3.2 转矩跟随响应仿真

在本次仿真中，保持转速和燃油消耗量在一段时间内不变，之后使增压柴油机在某时刻转速和燃油消耗量阶跃，通过BP-QPSO算法控制VGT开度，使增压柴油机具备转矩和过量空气系数跟随能力。增压柴油机转速和燃油消耗量变化见图11，增压柴油机运行结果见图12和图13。从图中可以看出，增压柴油机的转矩和过量空气系数可以在较短时间内达到期望值，并且转矩变化相对比较平稳，同时每个阶段的过量空气系数都可以稳定在1.7左右，使增压柴油机输出期望转矩。

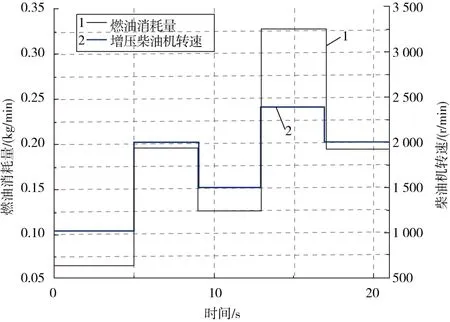
图11 柴油机转速以及燃油消耗量变化

图12 增压柴油机转矩变化

4 结语

1) 鉴于增压柴油机参数之间呈现出非线性，本文采用BP神经网络建立预测模型，对未来时刻进气流量和排气压力进行准确预测，为VGT的控制提供了依据。

图13 增压柴油机过量空气系数变化

2) 通过对普通PSO算法和量子PSO算法做对比，发现量子PSO算法调节参数少，同时适应度下降更快，结果相比于普通PSO表现更优。

3) 本文在两种响应仿真中，利用QPSO算法对VGT进行寻优，从仿真结果可以看出，该算法通过控制VGT开度，使增压柴油机转矩平稳运转至期望值，具备良好的转矩跟随能力。