气泡破裂及其诱发射流液滴释放过程的实验研究

李文强，杨宜昂，焦守华，柴 翔

(上海交通大学 核科学与工程学院，上海 200240)

核工程领域存在着广泛的气溶胶二次夹带现象，如反应堆熔堆事故后期，由衰变余热引发堆坑水沸腾产生大量气泡，气泡炸裂后产生的夹带液滴会导致大量的放射性物质持续释放到安全壳内。通常来讲，液面下上升的气泡接触液面后不会立刻破裂，而是经过一段时间的液膜排液效应后破裂，这段时间称为气泡表面寿命[1-2]。气泡破裂后会生成膜状液滴和射流液滴[3]，射流液滴是放射性气溶胶夹带的重要组成部分；随气泡直径的增加，射流液滴直径越来越大，而每次破裂产生的平均射流液滴个数逐渐降低直至不产生射流液滴[4]。目前，国际上大量学者多从物性角度考量其对破裂过程的影响，广泛探究了不同直径气泡表面的塌缩情况对射流液滴直径与射流液滴速度的影响规律[4-9]，也有大量学者总结了液体物性对射流液滴的影响[4，8-10]。然而，目前研究中对气泡表面寿命影响射流液滴释放过程的分析相对较少，仍有待进一步探索。

本文采用实验方法，通过高速摄像的方法捕捉不同直径下的气泡破裂过程及射流液滴的释放过程，获得气泡破裂后气泡空腔的演变过程，捕捉射流液滴的直径和速度，探究气泡直径和气泡表面寿命对射流液滴释放过程的影响规律。

1 实验装置

实验装置如图1所示，实验平台由侧视实验装置和俯视实验装置构成，两装置由注射泵、水箱、光源、气泡发生器、高速相机、电脑、高速相机PhantomV710L等组成。其中实验段水箱尺寸为200 mm×200 mm×600 mm的亚克力方箱，厚度为20 mm，气泡发生器上固定有内径为0.15～5 mm的不同毛细管，用于产生不同直径的气泡。在探究气泡表面寿命与射流液滴关系时采用侧视实验装置。实验时调整注射泵到较低注射速率，保证前一气泡破裂前下一气泡未出现，调整拍摄帧率为7 500帧/s，将高速相机中心置于气液交界面，气泡接触到液面瞬间时开始拍摄直到气泡破裂后产生射流液滴拍摄结束，用于获取气泡表面寿命和气泡破裂产生的射流液滴。在探究气泡表面寿命分布规律时采用俯视实验装置。当气泡上升到液面后，围板外的平行光源会照亮气泡区域，此时用相机开始捕捉直到气泡破裂，通过图像处理的方法获得气泡在视频出现的帧数获取表面寿命，采用500组表面寿命用以获取气泡表面寿命分布规律。实验工质采用去离子水，温度为室温18 ℃，气压为1×105Pa，相机的拍摄频率为120帧/s。根据Cosandey[11]和Gunther等[7]的研究，在堆芯融毁的严重事故中，产生的气泡平均直径为3 mm，本文中气泡直径的范围为2.5～7.11 mm。实验开始前，采用16×15的方格边长为10 mm的宫格板进行标定，标定结果显示放大倍数为0.07 mm/pixel。

a——侧视实验装置；b——俯视实验装置图1 实验装置示意图Fig.1 Schematic diagram of experimental facility

2 图像处理技术和不确定度

图2示出射流液滴速度处理流程图。为获取射流液滴速度，采用背景减除、对比度增强、边缘识别、膨胀腐蚀填充图像处理技术获取清晰的二值图像，并以此为基础得到射流液滴质心，通过两帧间质心运动距离最终获取射流液滴速度。

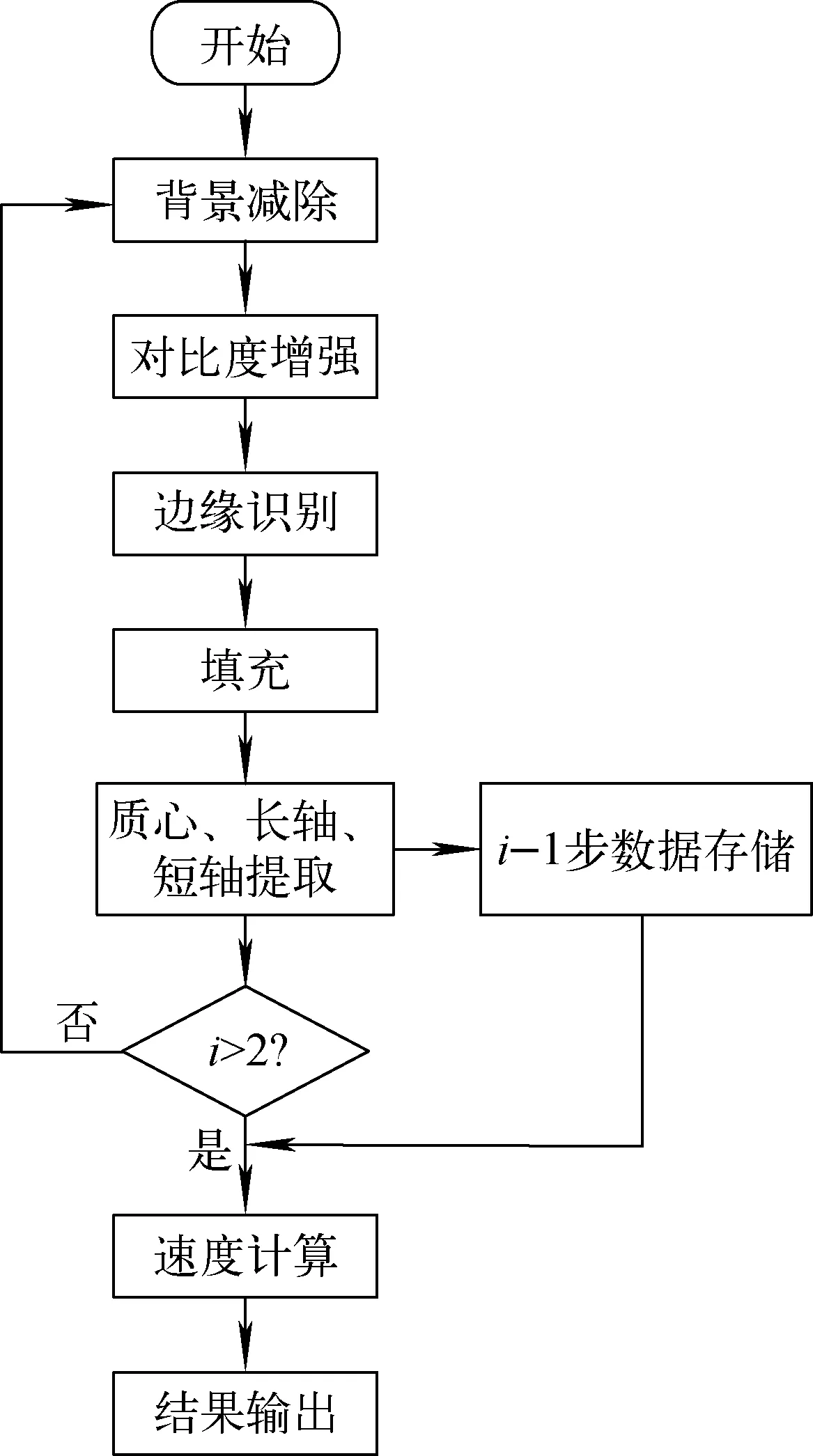
图2 射流液滴速度处理流程图Fig.2 Flow chart of image processing for jet droplet velocity

射流液滴速度按照瞬时速度定义计算。射流液滴质心位置计算公式为：

(1)

(2)

式中：xi和zi为像素的坐标；X和Z为计算求得的质心坐标；N为拍摄射流液滴所用帧数。

得到液滴质心后，液滴瞬时速度为：

(3)

(4)

图3示出气泡表面寿命获取处理流程图。气泡表面寿命计算时需首先进行首末帧识别，若连续两帧图片中气泡个数由0变为1时，认定为首帧，若连续两帧图片中目标个数由1变成0，认定为末帧，根据首末帧便可算出气泡表面寿命。

图3 表面寿命获取处理流程图Fig.3 Flow chart of image processing for surface lifetime

图4示出射流液滴长轴短轴示意图，根据图像处理程序可获取射流液滴的长轴和短轴长度，分别记做a和b，射流液滴直径d为：

(5)

获得直径后，射流液滴动能E为：

(6)

式中：M为射流液滴质量；u为射流液滴速度；ρ为水的密度。

图4 射流液滴长轴、短轴示意图Fig.4 Schematic diagram of major axis and minor axis of jet droplet

根据不确定度传递公式，速度的不确定度εu为：

εu=

(7)

式中：Z1、Z2分别为目标运动前后两帧的像素差；εZ1、εZ2、εΔt、εs分别为拍摄第1帧像素的不确定度、拍摄第2帧像素的不确定度、时间的不确定度和相机放大倍数的不确定度。

射流液滴动能的不确定度εE为：

(8)

式中，εa、εb分别为射流液滴长轴不确定度和射流液滴短轴不确定度。

经计算，射流液滴速度和动能的相对不确定度分别为4.64%和20.58%。气泡表面寿命不确定度由拍摄相机的频率决定，相对不确定度为1.63%。

3 实验结果与讨论

在气泡破裂前，液膜依次经过快速抽干效应、黏性排空之后快速减薄至μm量级的不稳定厚度。受到边际再生效应的影响，液膜经常在气泡根部发生刺穿效应[12]。刺穿效应发生后，气泡液膜从刺穿点向后收缩并向气泡边缘处运动，由于收缩液膜不再处于力平衡状态，因此液膜会断裂形成不稳定射流，也就是通常所说的膜状液滴。在气液交界面之下，表面张力波快速形成并在气泡空腔底部快速聚集生成射流并推动射流向上，最后，射流前沿断裂生成射流液滴，整个过程如图5所示。

图6示出直径为5.83 mm的气泡在到达气液分界面之后的不同破裂过程。由图6可见：时间轴上方的气泡在15.917 5 s之后发生破裂，破裂后的气泡释放了1个射流液滴；时间轴下方的气泡仅在5.883 5 s之后即发生破裂，破裂后的气泡并未释放射流液滴。实验结果表明，气泡表面寿命与射流液滴的释放有着密切关系，气泡表面寿命越长，越容易生成射流液滴。

图6 不同气泡表面寿命下射流液滴生成示意图Fig.6 Schematic diagram of jet droplet generation of different bubble surface lifetime

图7 射流液滴动能与气泡表面寿命的关系Fig.7 Jet droplet kinetic energy vs. bubble surface lifetime

气泡表面寿命除影响射流液滴释放外，其对射流液滴的动量和动能也有着密切关系。图7示出直径为5.83 mm的气泡所释放的射流液滴动能与气泡表面寿命的关系。对图7中数据拟合可得到射流液滴动能与气泡表面寿命的关系，如式(9)所示，拟合的相关系数为0.684 4。实验结果表明：射流液滴动能随气泡表面寿命的增加而增加；当气泡表面寿命小于4 s时气泡破裂不会产生任何射流液滴。图8示出18 ℃去离子水中直径为5.83 mm的气泡500组气泡表面寿命的分布。由图8可看出，当气泡直径为5.83 mm时，95%的气泡表面寿命小于4 s，仅有少于5%的气泡破裂后有可能产生射流液滴。

图8 18 ℃去离子水中5.83 mm气泡表面寿命的分布Fig.8 Bubble surface lifetime distribution with diameter of 5.83 mm in 18 ℃ deionized water

1.53×10-7

(9)

上述实验结果表明，随气泡表面寿命的增加，破裂气泡更容易产生射流液滴且射流液滴的速度也随之变大。该现象可能与气泡滞留在气液分界面时液膜的减薄过程相关。根据Lhuissier等和Poulaine等的理论[13-14]，当气泡滞留在气液分界面时，其液膜厚度随时间的减薄规律为：

(10)

式中：h为液膜厚度；a为气泡的毛细长度；R为气泡在液面上飘浮时的侧视液膜圆弧半径；μ为水的动力黏度；t为气泡在水中的表面寿命。

根据式(10)，气泡破裂前的表面寿命越长，破裂时液膜厚度越小，在时间上遵循2/3方衰减规律。根据Taylor-Culick关系[15-16]，气泡破裂后液膜回退速度与厚度的关系为：

(11)

式中：σ为气泡在液面的表面张力；ρ为水的密度；v为气泡破裂之后的液膜收缩速度。

式(11)表明，液膜越薄，液膜收缩的速度越快。随液膜收缩速度的增加，破裂气泡更容易产生射流液滴并加速射流液滴的运动。

为探究气泡直径Db对气泡表面寿命的影响，图9示出不同气泡直径下表面寿命的频率分布和拟合得到的概率密度分布。由图9可见，随气泡直径的增加，气泡表面寿命分布峰值逐渐趋向于0，气泡表面寿命的分布表现出明显的两个不同分布，分别为Rayleigh分布和指数衰减分布。当气泡直径为2.51、4.89和5.12 mm时，气泡表面寿命呈现Rayleigh分布；当气泡直径为5.32、5.83和7.11 mm时，气泡表面寿命呈现指数衰减分布。

表1列出不同直径气泡表面寿命的概率密度函数P(t)。由表1可见：气泡表面寿命分布为Rayleigh分布时，其气泡表面寿命的均值较大，气泡在液面停留时间较长，因此气泡破裂后将会大概率产生射流液滴；气泡表面寿命为指数衰减分布时，气泡表面寿命的均值较小，虽仍可能产生射流液滴，但释放射流液滴的概率小于5%。

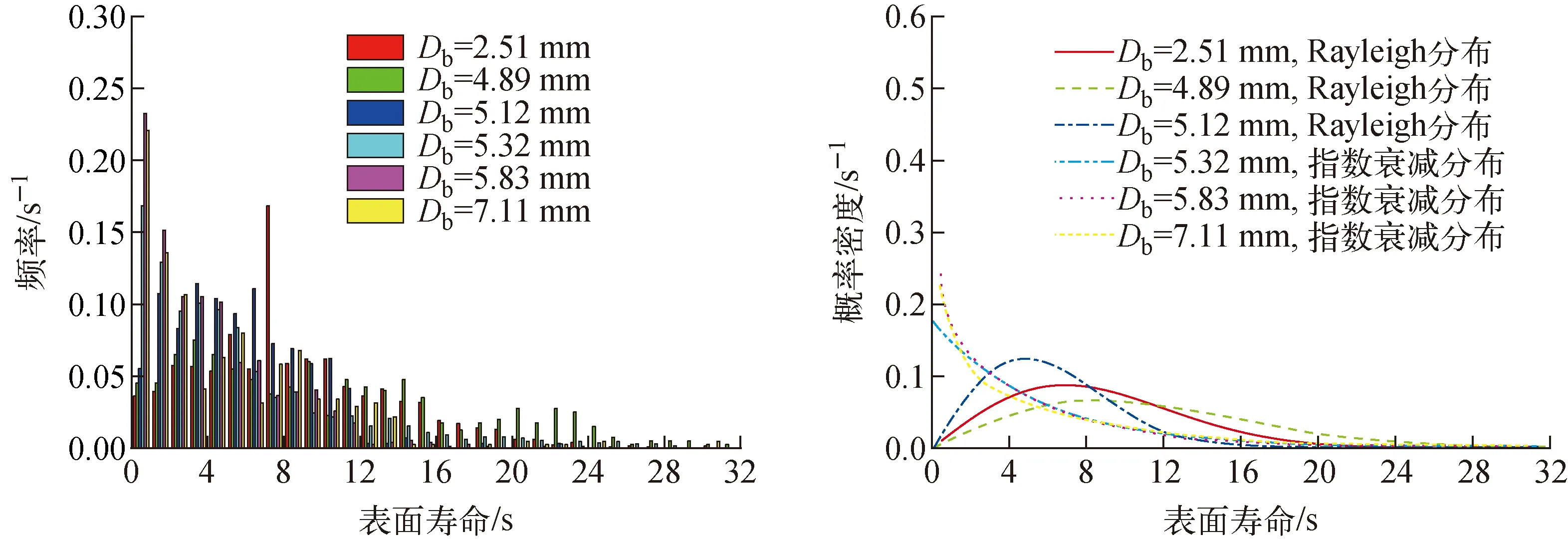
图9 不同直径气泡表面寿命的频率分布和概率密度分布Fig.9 Frequency distribution and probability density distribution of bubble surface lifetime with different diameters

表1 不同直径气泡表面寿命的概率密度函数Table 1 Probability density function of bubble surface lifetime with different diameters

射流液滴速度u与气泡直径Db的关系如图10所示。由图10可见，从射流液滴速度与气泡直径趋势上而言，射流液滴速度随气泡直径的增加而降低，这与Spiel[5]、Elisabeth等[9]和Suzuki等[17]的实验结果一致。

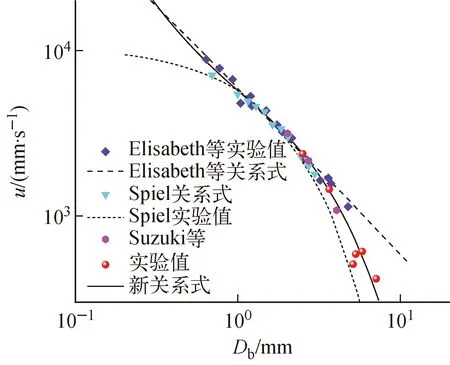
图10 射流液滴速度与气泡直径的关系Fig.10 Jet droplet velocity vs. bubble diameter

此外，需要注意的是当气泡直径大于5.5 mm后，Elisabeth等[9]幂衰减拟合关系式外推结果过高估计了射流液滴速度，而Spiel[5]指数衰减拟合关系式外推结果过低估计了射流液滴速度。在之前的研究中，学者们通常低估了气泡破裂产生射流液滴的临界直径，以Suzuki等[17]为代表的学者认为直径大于5.5 mm的气泡在破裂后不能产生射流液滴，而本文实验结果表明，气泡直径大于5.5 mm后，气泡破裂后仍能产生低速的射流液滴。考虑到现有的Elisabeth等关系式和Spiel关系式在气泡直径较大的情况下与实验值有明显的偏差，为能在更大气泡直径区间内描述射流液滴速度与气泡直径，本文通过收集文献实验数据和现有实验数据，并综合考虑Elisabeth等关系式和Spiel关系式，拟合得到了新的关系式：

u=5.86e-864.72R+4.58×10-5R-1.703 9

(12)

采用RMS误差衡量新关系式的精度，其定义如下：

(13)

式中：ue，i为射流液滴速度实验值；us，i为关系式获得的射流液滴速度。

表2列出Spiel、Elisabeth等关系式和新关系式的适用范围和RMS误差，经计算Spiel和Elisabeth等关系式的RMS误差分别为22.73%和33.33%，新关系式RMS误差为11.75%，新关系式具有更高的计算精度。

表2 不同关系式的适用范围和RMS误差Table 2 RMS error and scope of application for different correlations

4 结论

本文通过高速摄像的方法捕捉了不同直径下的气泡破裂过程及射流液滴的释放过程，探究了气泡直径和气泡表面寿命对射流液滴释放过程的影响，主要结论如下。

1) 气泡表面寿命影响气泡破裂后射流液滴的产生过程。当气泡直径为5.83 mm时，表面寿命小于4 s的气泡在其破裂后不会产生任何射流液滴。射流液滴的出射速度随气泡表面寿命的增加而增加。其原因可能为：气泡表面寿命越长，破裂后液膜收缩速度越快，进而加速了射流液滴的产生。

2) 气泡表面寿命呈现出两种不同的概率分布形式：Rayleigh分布和指数衰减分布。当气泡直径较小时，其呈现Rayleigh分布的特征；当气泡直径较大时，其逐渐呈现指数衰减分布特征。

3) 当气泡表面寿命为Rayleigh分布时，气泡表面寿命均值较大，气泡破裂后大概率能产生射流液滴；随气泡直径的增加，其表面寿命分布转变为指数衰减分布，其表面寿命均值趋向于0，气泡破裂后产生射流液滴的概率较小。该发现为从气泡表面寿命角度解释气泡破裂产生射流液滴的机理提供了实验数据，也为如何降低射流液滴生成提供了一个可能的方向。

4) 射流液滴出射速度随气泡直径的增加而降低，当气泡直径大于5.5 mm时，射流液滴速度介于Spiel指数衰减拟合关系式和Elisabeth等幂衰减拟合关系式的预测值之间，根据实验数据获取的射流液滴速度与气泡直径的新关系式，具有更高的精度和更好的适用性。