HTR-10蒸汽发生器的建模及分析
2021-02-03陈稳,孙俊,眭喆
陈 稳,孙 俊,眭 喆
(清华大学 核能与新能源技术研究院,先进反应堆工程与安全教育部重点实验室,北京 100084)
HTR-10是由清华大学核能与新能源技术研究院设计、建造的球床模块式高温气冷堆,其中蒸汽发生器(SG)是将反应堆能量传递给常规岛产生合格品质蒸汽的关键部件。HTR-10的模拟机可用于反应堆技术改造验证及操作人员培训,而其中关键部件蒸汽发生器的模拟涉及到一、二回路相关参数的耦合和二次侧工质水的相变化,需重点关注。
HTR-10采用螺旋管式直流蒸汽发生器,前人已针对此类蒸汽发生器开展了多种研究:段冰[1]通过编写程序研究了HTR-10蒸汽发生器中的两相流不稳定性;黄晓津[2]为实现HTR-10蒸汽发生器控制系统的设计、分析,建立了静态结果具有较好精度和动态结果符合热工水力学特性的仿真模型;周云龙等[3]研究了多头螺旋管式换热器的设计方法并给出设计计算时采用的传热和压降计算关系式;Yang等[4]通过实验数据进一步验证了TASS/SMR代码适用于先进一体化反应堆中螺旋管式蒸汽发生器的传热计算;连强等[5]基于RELAP5程序开发了计算螺旋管式直流蒸汽发生器的模块,并通过实验数据及程序对比验证了新开发程序在螺旋管式直流蒸汽发生器热工水力分析中的适用性。上述研究通过开发的计算程序进行蒸汽发生器的热工水力设计及分析,且相关研究也可满足相应的需求。
本研究针对HTR-10模拟机开发的蒸汽发生器模型,为满足模拟机需求,搭建的蒸汽发生器模型首先要保证实时计算,为此可在一定程度上牺牲模型的精度。前人同样针对模拟机应用背景下的螺旋管式蒸汽发生器开展了相关研究:高强等[6]将THERMIX/BLAST程序开发为独立模块嵌入vPower仿真平台,开发了HTR-PM工程模拟机系统HTR-PMsim,实现了包含蒸汽发生器的系统的稳态和动态仿真,但未实现实时仿真模拟;刘丹等[7-8]基于vPower平台搭建了高温气冷堆HTR-PM模拟机的可实时计算的蒸汽发生器模型,模型的稳态和动态计算结果均可反映蒸汽发生器中的热工水力特性。本文采用一体化仿真建模支撑平台vPower开发HTR-10模拟机的蒸汽发生器模型,讨论模型的节点划分方案并通过分析稳态工况下蒸汽发生器内部参数的分布和氦气阶跃时主要参数的变化过程,验证模型的准确性和适用性。
1 蒸汽发生器模型
HTR-10采用立式布置的螺旋管式直流蒸汽发生器,包含30个模块式小弯曲半径换热组件,组件示意图如图1所示。螺旋管束组件同样采用立式布置的方式,每个组件由缠绕在中心管上的螺旋管和直管连接形成。一次侧工质氦气经堆芯加热后由热气导管进入蒸汽发生器,氦气在环形空腔中自上而下掠过螺旋管束,在此过程中通过金属管壁将热量传递给二次侧工质;二次侧工质水自下而上从管束内部流过,并在此过程中不断吸收氦气放出的热量,经过预热段、蒸发段和过热段,成为过热蒸汽,最终进入汽轮机做功。建模时将热力学参数相近的区域划分为同1个控制体节点,形成最终的模块矩阵模拟整个蒸汽发生器部件。模型流动状态参数通过流体网络理论进行求解,热力学参数则通过换热模型理论进行求解。蒸汽发生器的主要设计参数和结构参数分别列于表1、2。由表2可见,针对气水两相流动的稳定性问题,HTR-10蒸汽发生器的传热管采用了变管径设计。此外,设计时主要的换热部分为传热管段,建模时两侧的换热计算也只考虑传热管段两侧通过金属管壁的热量传递过程。

图1 蒸汽发生器模块式组件[9]Fig.1 Structural scheme of SG modular assembly[9]
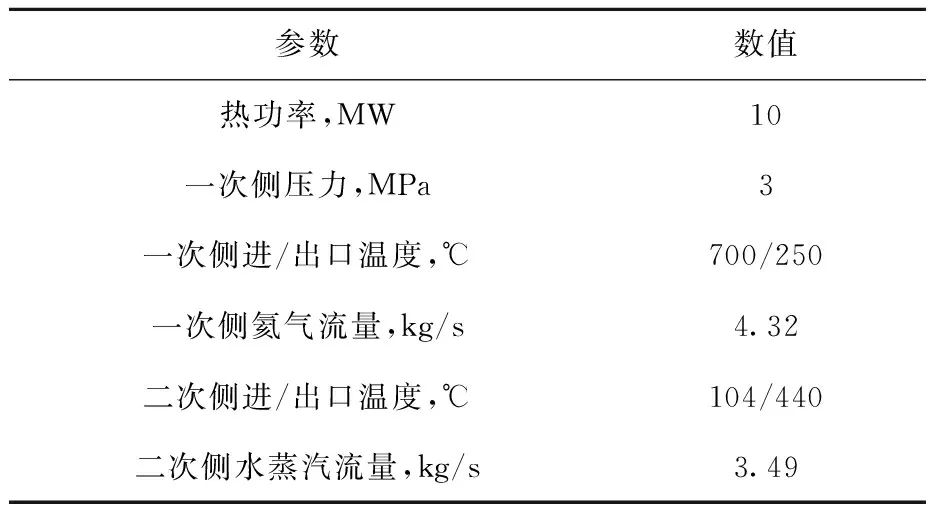
表1 蒸汽发生器的主要设计参数Table 1 Main design parameter of steam generator

表2 蒸汽发生器的主要结构参数Table 2 Main structural parameter of steam generator
1.1 流动计算理论基础
蒸汽发生器模型的流动计算以流体网络为理论基础,该理论已多次应用于高温气冷堆堆芯和蒸汽发生器的建模研究并取得了较好的效果[7-8,10-13]。依据HTR-10蒸汽发生器中工质的流动特点,在vPower平台中通过节点、支路连线和阻力模块模拟对应的流道。节点模拟具有实际容积的控制体,支路则模拟工质的流通路径,粘贴于支路上的阻力模块用于求解流动时的压降。
工质的流动过程采用一维流道模拟,一维流道中流动关系以实际的支路压降计算关系式[1]为基础,并将其处理为在vPower平台中适用于流体网络模型的形式。vPower平台中的处理方式如下,首先将一维支路的阻力特性表示成如下关系式:
(1)
其中:w为流量;ρ为密度;Δp为支路两端节点压差;g为重力加速度;Δh为支路两端高度差;A为支路的流通能力系数。A的求解方法如下:
(2)
其中,Δp*为依据压降计算模型得到的阻力特性参数,计算时采用压降计算模型和密度的乘积进行求解。将方程(1)在t+1时刻进行一阶泰勒展开,得到支路的线性化压力方程,即:
wt+1=Rb1p1,t+1-Rb2p2,t+1-Cb
(3)
(4)
(5)
其中:下标t表示当前时刻,t+1为下一时刻;Rb1、Rb2和Cb为系数;p1、p2为节点压力。
针对流体网络中1个多条支路相交的节点,列出其质量守恒方程为:
(6)
其中:V为节点容积,计算时采用输入的定值;t为时间;p为节点压力;h为比焓。对于该内节点,假设与其连接的支路共n条,其中m条支路为节点和上游的m个压力分别为p1,p2,…,pm的节点或边界点相连,另外有n-m条支路为节点和下游的n-m个压力分别为pm+1,pm+2,…,pn的节点或边界点相接,各支路的流量为wi(i=1~n),漏入该节点的流量为wLE,该节点的泄漏流量为wLL。
对于节点质量守恒方程中的微分项,在1个时间步τ上采取如下的差分方式:
(7)
将方程(3)和(7)代入方程(6)得到:
(8)
对于流体网络中全部内节点,均可列出其节点质量守恒方程,所有方程构成形如AX=B的线性方程组,求解方程组得到各节点的压力以及对应支路中的流量,从而得到模型中的压力和流量分布。
1.2 换热模型理论基础
结合表1、2及上述对蒸汽发生器模型换热过程的介绍可知,蒸汽发生器中的换热过程主要为一、二次侧工质逆向流动时的对流换热和传热管内部的径向导热过程,且换热绝大部分集中于传热管。因此,换热过程的计算基于以下假设:1) 固体模块间不考虑沿流动方向的换热;2) 从氦气侧经金属管壁到水侧的换热只发生在传热管部分,其他部分作绝热处理;3) 对于一、二次侧节点认为毕渥数趋近于0,即内部热阻远小于外部的对流换热热阻,因此1个节点只有1个特征温度;4) 管道横截面上流体的温度、压力等特性均匀,气液两相压力相同;5) 流体的总能忽略动能、重力势能、界面剪切力做功等,只考虑比焓。
1) 二次侧换热的数学模型
二次侧工质流经蒸汽发生器时,依据能量守恒关系可得到二次侧节点比焓的微分方程:
(9)
其中:下标w代表水侧;τ为时间;h为水侧工质的比焓;hin为水侧节点入口工质的比焓;Qw为工质的对流换热量;Mw为质量流量;Vw为节点的容积;ρw为密度。此外,在离散求解该微分方程时采用显式格式,即求解时方程右侧参数均为上一时间步的值。
水侧工质的对流换热量Qw求解方程如下:
Qw=hwAw(T2-Tw)
(10)
其中:hw为工质流动时的对流换热系数;Aw为节点的对流换热面积;T2为金属管壁内侧壁温;Tw为水侧工质温度。
由于二次侧工质为水,电站运行时工质在管道内流动过程中会发生流型的转变。此时,需要依据工质的热力状态判断所处的流型状态,从而选择对应的换热和阻力计算关系式。模型中通过计算二次侧节点的干度判别工质所处状态,计算公式如下:
(11)
其中:hw,sat为工质的饱和水比焓;hs,sat为工质的饱和蒸汽比焓。
2) 一次侧换热的数学模型
氦气在掠过传热管时,依据能量守恒关系可得到计算氦气侧节点温度的微分方程:
(12)
其中:下标g表示氦气;T为氦气节点的温度;Mg为质量流量;cp,in、Tin分别为流入节点工质的比定压热容和温度;cp为节点工质的比定压热容;Qg为放热量;Qs为考虑氦气在返回氦气风机时向蒸汽发生器外壳散热时产生的损失;Vg、ρg分别为节点的体积以及节点工质的密度。同样,在离散求解微分方程(12)时采用显示格式。
方程(12)中的Qs根据设计计算值进行输入,Qg则是氦气流经管束外部时的对流放热量,计算方程如下:
Qg=hgAg(Tg-T1)
(13)
其中:hg为工质流动时的对流换热系数;Ag为氦气侧节点的对流换热面积;T1为金属管壁外侧壁温;Tg为氦气侧节点温度。
3) 金属管壁换热的数学模型
HTR-10蒸汽发生器换热情况是传热管和其中的污垢层内部为导热、两侧为对流换热。在建立传热管壁的换热模型时,引入以下假设:(1) 考虑到管壁和污垢厚度远小于管径,将传热管内部换热模型视为一维平板导热模型,且金属管壁和污垢内部的温度为线性分布;(2) 对于固体模块的热容,建模时考虑金属管壁的热容性并依据实际模块的参数给出模块计算所需的密度、比热等参数,但不考虑污垢层的热容性。基于以上假设,HTR-10蒸汽发生器模型中传热管的换热情况如图2所示。

图2 金属管壁导热模型示意图Fig.2 Heat conduction model in heat transfer tube
传热管的换热模型需计算传热管外壁面温度T1,金属管壁和污垢层分界面的温度Tcr以及传热管内壁面温度T2,通过联立求解3个能量守恒方程得到上述待求温度。
依据金属管壁的能量守恒关系,管壁所吸收的能量等于一次侧传递的能量减去金属模块向污垢层传递的热量,即:
(14)

在金属管壁和内侧污垢层接触界面x1位置应满足热流连续性,热流连续性方程为:
(15)
其中,λcr为污垢层的导热系数。
依据假设2,不考虑污垢层的热容性,所以污垢层的能量守恒关系为从金属管壁导入的热量等于污垢层向二次侧工质传递的热量,其能量守恒方程为:
(16)
至此,可联立方程(14)~(16)求解得到所需的温度T1、Tcr、T2。模型计算中所采用的换热和阻力压降计算关系式使用刘丹等[7]所采用的关系式,其中临界雷诺数的计算则采用更加针对HTR-10蒸汽发生器模型的公式[9]。
1.3 蒸汽发生器模型组态
依据螺旋管式直流蒸汽发生器的结构和工质流动特点,基于vPower平台搭建了蒸汽发生器的模型。模型中1个组件的基本组态示于图3,组件的同一高度处分为氦气侧节点、金属模块节点和水侧节点,同时组件沿流动方向(高度方向)进行节点划分;整个蒸汽发生器含有30个组件,因而搭建了30条如图3所示的组件通道。所有组件一、二次侧的进出口分别连到统一的边界点,两侧工质分别由对应的边界点流入,而后分流入各组件模型,最后所有组件的一、二次工质分别流入对应的氦气和水蒸气边界点,以此模拟工质从流入到流出蒸汽发生器的过程。

图3 单组件模型组态Fig.3 Configuration of single assembly
2 结果与讨论
本文首先对模型的节点划分方案进行了讨论,为后续研究确定合理的模型划分方案。而后,分析了模型稳态和动态计算结果的精度和合理性:工质出口温度将是始终关注的重要参数,此外,稳态工况关注模型分布参数的准确性,动态工况关注主要参数动态响应过程的合理性。
2.1 模型节点划分方案分析
HTR-10模拟机实时模型最大步长为250 ms,而蒸汽发生器作为其中的关键部件模型,既要保证计算的实时性,同时还要具有一定精确度,因此,节点数量的划分要平衡计算效率和精度。本文针对组件沿流动方向采用3种节点划分方案:96节点均分、24节点均分和24节点加密方案,其中24节点加密方案通过调整节点布置对工况变化剧烈的恶化沸腾区域附近进行了加密布置,3种方案具体的节点分布示于图4。本文针对3种划分方案的计算结果进行比较,并分析不同节点划分方案的适用性。

图4 节点划分方案Fig.4 Module division scheme
图5为3种节点划分方案的模型在100%稳态工况下计算所得的分布参数。二次侧温度、干度、换热系数、热流密度、氦气侧换热系数和传热管与水侧温差的对比结果表明:3种方案的分布参数计算结果相差不大,但24节点加密方案的计算结果与96节点均分方案在总体上和图中圈出的烧干沸腾区域符合得更好;由于节点为集总参数模型,且图4中圈出的烧干沸腾区域占比很小,24节点均分方案在这一区域的节点划分相对较大,模型计算时易忽略从烧干沸腾区到过热区这一变化过程,因此24节点加密方案中在该区域及附近区域进行了加密,而过冷区参数变化平缓的区域则增大节点尺寸,从而获得了和96节点均分方案更接近的计算结果。同时,96节点均分方案的模型在1个时间步内耗时少于50 ms,24节点方案耗时小于30 ms,均满足计算的时间步长要求。综合来看,在培训使用的工程模拟机计算精度要求下,3种节点划分方案均可满足要求,但若是搭建用于工程设计、事故分析这样的精度要求更高的模拟机系统,24节点加密和96节点均分方案更为合适。由于24节点加密划分方案对于计算能力较弱且后续继续扩大模型覆盖范围和连接HTR-10模拟机其他系统的场景更为合适,因此后续研究基于96节点均分方案进行。

图5 3种节点方案参数分布对比Fig.5 Comparison of parameter distribution in three division schemes of modules
2.2 模型稳态计算结果与分析
基于上述分析,为获得更高精度,进行稳态计算时采用组件均分为96节点的方案,利用96节点的模型计算100%和30%功率水平下的稳态工况。在给定的边界条件(氦气流量、氦气进口温度、氦气出口压力、给水流量、给水温度、蒸汽出口压力)下,计算氦气和蒸汽出口温度,结果列于表3。比较表3中氦气和蒸汽出口温度在稳态工况下的计算结果和设计值发现,模型的主要出口参数与设计值最大相对误差不超过2.10%,这一精度满足模拟机的仿真建模要求。
稳态工况计算结果表明,进出口参数计算精确度较高,满足模拟机仿真要求,但仍需对蒸汽发生器模型内部参数分布的合理性进行分析,分析时重点关注状态变化复杂的二次侧工质的参数。96节点均分方案下的蒸汽发生器模型在100%功率水平稳态工况下的内部温度、二次侧干度、二次侧换热系数、二次侧热流密度及传热与水侧温差分布示于图6。

表3 蒸汽发生器模型稳态计算结果与设计值对比Table 3 Comparison between simulation results and design parameters in steady-state condition

图6 100%稳态工况内部参数分布Fig.6 Parameter distribution of SG model in full power condition
在蒸汽发生器中,二次侧工质在自下而上流经螺旋管内部过程中不断吸热,除二次侧工质位于两相区时由于压降导致饱和温度下降而呈现微弱下降趋势外,一、二次侧工质及金属温度均随传热管长度的增加而不断上升。且由于氦气侧换热系数量级为1.0×103W/(m2·℃),氦气和金属管壁温差远大于金属管壁和水侧温差。而二次侧工质在传热管内流动时不断吸热,在传热管0~37.5%长度内,工质干度为0,仍为过冷水状态,此时工质换热系数缓慢上升,传热管与水侧温差下降,热流密度也呈缓慢下降趋势;在传热管37.5%长度处,工质进入两相区,换热系数迅速增大,传热管与水侧温差也缓慢上升,使得热流密度也迅速上升;而在传热管85.4%长度处,工质达到烧干沸腾临界干度,进入烧干沸腾区,发生传热恶化,此时对流换热系数达到峰值后骤降,导致传热管和二次侧温差迅速上升,热流密度则在达到峰值后小幅下降;随着蒸汽发生器高度的增加,在传热管87.5%长度处工质干度达到1,成为过热蒸汽,对流换热系数继续下降,温差继续增加到峰值后下降,热流密度继续下降。通过对传热管100%稳态工况下分布参数的分析可得,96节点模型划分方案的稳态模拟结果合理,可正确反映螺旋管式直流蒸汽发生器的换热与流动特性。
2.3 氦气质量流量阶跃
针对蒸汽发生器模型的验证,除要保证稳态计算结果的准确性,还应验证动态工况下计算结果的合理性,分析动态工况下的计算结果也有助于掌握相关参数在动态过程中的变化规律。考虑电站的实际运行情况,本文以100%功率稳态工况(表4)为基础进行动态工况模拟,并在此基础上引入氦气入口质量流量阶跃变化来模拟主氦风机加、减速过程,在模拟氦气流量阶跃变化时,将两侧入口设置为可变流量边界,两侧出口则设置为固定压力边界。以表4中100%功率稳态工况为初始工况,在运行30 s后引入氦气质量流量±1%和±3%阶跃,记录并分析模型的动态响应情况,结果示于图7。
由图7可见,氦气质量流量阶跃增加,氦气出口温度先迅速上升而后缓慢上升,由于金属管壁和二次侧工质具有一定热容,蒸汽出口温度上升过程相较于冷氦温度更为缓慢,且一、二次侧出口温度上升幅度和氦气质量流量增加量呈正比,反之亦然。氦气质量流量阶跃变化后,二次侧一些节点在温度、干度等状态变化过程中可能导致传热和压降计算模型变化,因而蒸汽出口温度在过程中会有小幅波动,而流量阶跃变化幅度越大,水侧温度变化越大,此现象也更明显。同时可见,由于一般螺旋管式的直流蒸汽发生器热惯性较小,且HTR-10的蒸汽发生器高度在1 m左右,热容很小,蒸汽发生器自阶跃发生后至再次平衡的时间也很短,模拟的工况中再平衡时间在60 s左右,且氦气流量阶跃变化幅度越小,模型再平衡时间越短。

表4 蒸汽发生器模型动态仿真的初始工况主要参数Table 4 Main parameter of initial condition of dynamic simulation of steam generator model
图8为氦气侧流量阶跃上升3%时氦气侧主要参数的动态响应过程。由图8可见,初始工况运行30 s后,由于氦气质量流量阶跃上升,氦气侧传热系数突然上升,此时金属管壁在这一瞬间温度还未显著变化,因此换热量也会阶跃上升。同时可见,氦气侧换热系数阶跃上升幅度小于流量阶跃增加幅度(换热计算关系式中氦气侧换热系数Nu和Re之间的指数关系决定了这种变化关系),而氦气进口温度保持不变,依据能量守恒关系,氦气出口温度也会迅速上升。之后,由于氦气侧放热量的增加,金属管壁逐渐升温,水侧吸热量也会上升,又因为给水流量和给水温度保持不变,因此出口蒸汽温度也会上升,但由于水侧和金属管壁具有一定热容,上升速度较慢。同时随着金属管壁和水侧的升温,氦气侧换热系数基本稳定的情况下,氦气侧放热量有所减小,在热氦温度和氦气流量不变的情况下,后续冷氦温度缓慢上升。因此,后续过程中冷氦温度和蒸汽出口温度上升梯度逐渐减小并最终稳定在一个新的状态。自阶跃发生,经过约60 s,冷氦温度再次稳定在258.56 ℃,与初始工况相比上升4.48 ℃;出口蒸汽温度则稳定在464.29 ℃,较稳态工况上升24.42 ℃。
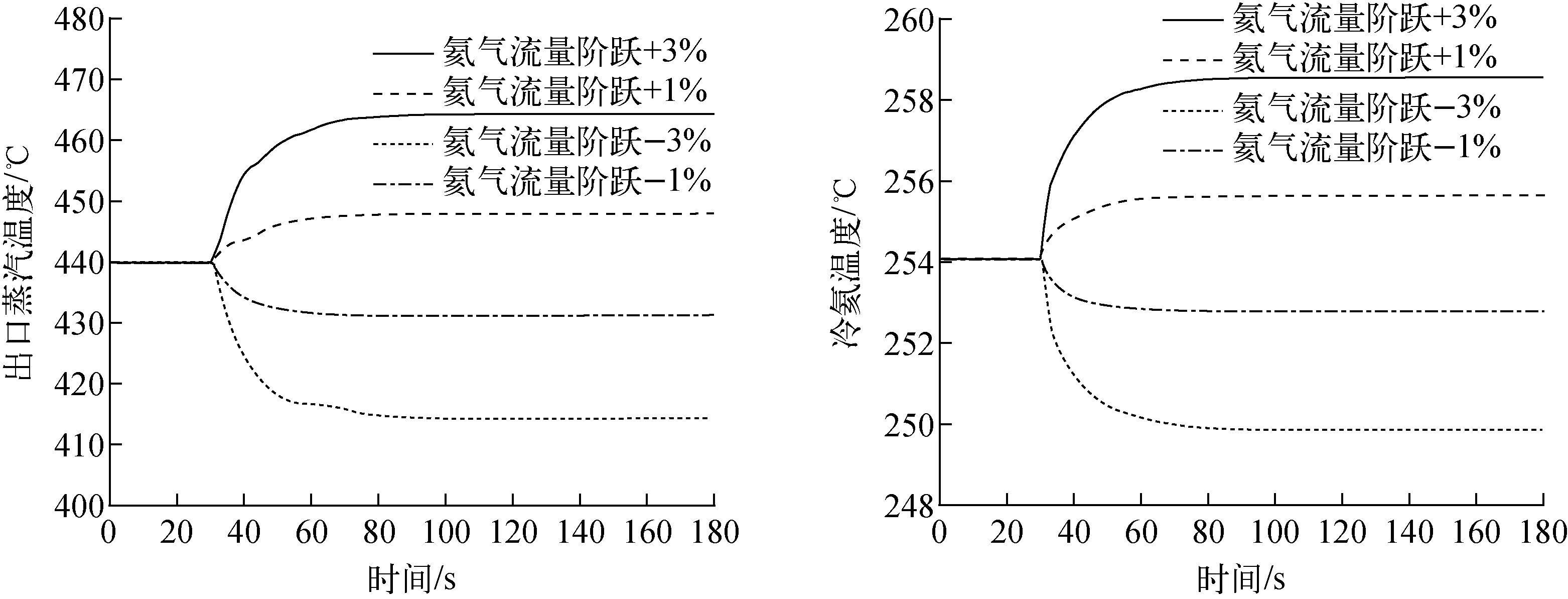
图7 氦气质量流量阶跃工况下出口温度响应曲线Fig.7 Response curves of outlet temperature under helium mass flow step conditions
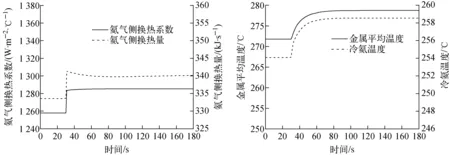
图8 氦气质量流量+3%时氦气侧主要参数响应曲线Fig.8 Response curves of main parameters of SG model when helium mass flow+3%
氦气流量阶跃变化的动态过程表明,在氦气流量阶跃变化时,氦气侧的部分参数会产生不同程度的阶跃响应,而一次侧产生的变化主要通过换热量的变化影响金属管壁和二次侧,由于金属管壁和二次侧具有一定比热容,一次侧流量的阶跃变化造成的影响向水侧传递的过程会有一定的延迟,造成二次侧的参数响应过程较慢且没有明显的阶跃现象。蒸汽发生器模型在不同幅度和不同方向的氦气流量阶跃变化的动态响应过程中均体现了类似的规律。
3 结论
本文采用vPower搭建了适用于高温气冷堆HTR-10模拟机的蒸汽发生器模型,并对稳态工况和1个动态工况进行了模拟。稳态工况计算结果表明,关键出口参数的精确度满足要求,蒸汽发生器分布参数合理;动态工况计算结果符合螺旋管式直流蒸汽发生器的基本物理特性。同时,针对不同节点划分方案的讨论既进一步证实了稳态计算结果的合理性,也为不同方案的适用性提供了建议。本研究为后续HTR-10全范围模拟机的开发奠定了良好基础。
