两种脉冲信号包络提取方法的联系及性能分析

石 荣，邓 科，阎 剑

(电子信息控制重点实验室，四川 成都 610036)

0 引言

雷达信号脉冲描述字(Pulse Description Word，PDW)是雷达侦察信号处理中最基本的数据单元[1-2]，PDW中脉冲到达时间、脉冲宽度和脉冲幅度这3个时域参数的测量都依赖于脉冲信号包络的有效提取[3-4]。不仅如此，脉冲包络在雷达信号分选、型号和个体识别等应用中发挥着关键作用[5-7]。脉冲包络提取的传统方法通常采用平方率检波[8-9]，按照输入信号的不同，又可细分为：① 射频信号的平方率检波，采用模拟电路实现，如各种频段的模拟检波器；② 中频信号的平方率检波，在ADC采样之后，利用FPGA处理来实现数字检波。无论是模拟方式，还是数字方式，其基本数学模型都是对输入信号进行平方运算，然后再经过低通滤波器输出检波结果。除此之外，在中频数字信号处理中还可以通过希尔伯特变换来获得实信号对应的解析信号形式，而解析信号的模值就直接对应了该实信号的包络分量[10]，所以该检波方法又被称为基于希尔伯特变换的包络检波。

随着高速宽度ADC器件及数字信号处理技术的发展[11-12]，在现今的各种信号处理中普遍采用数字检波器来完成脉冲信号的包络提取[13]，而最典型的2种方法就是平方率包络检波与基于希尔伯特变换的包络检波。尽管经典教科书与部分文献对上述方法都进行过比较详细的介绍与分析，但是已有文献所给出的平方率包络检波的数学模型并不具备普遍性，仅针对脉冲信号的频率位于检波带宽的正中央这一特殊情况进行了分析[8,14]，而实际上脉冲信号的频率在整个检波带宽范围内是随机分布的。针对这一问题，本文进行了模型的改进，并给出新的理论分析模型。另一方面，已有文献并没有对上述2种典型的脉冲信号包络提取方法之间的联系展开研究[8-9]，而本文通过理论分析后指出，基于希尔伯特变换的包络检波是平方率包络检波的一个特例，从而为上述2种方法的工程选用提供了理论指导。最后在此基础上，利用构建的数字检波模型，给出了雷达信号侦察灵敏度的新计算公式，从而为雷达侦察数字接收机的设计以及侦察性能的准确度量与评估提供了重要参考。

1 平方率包络检波的模型

检波器输入端的信号sin(t)为：

sin(t)=sa(t)+n(t)，

(1)

式中，sa(t)=A·cos(ω0t+θ)表示幅度为A、载波频率为ω0、初相为θ的雷达脉冲信号；n(t)表示带宽为Bn的零均值带限高斯白噪声，其上下限频率分别记为ωn,up，ωn,down，显然Bn=ωn,up-ωn,down。在上述信号模型中，sa(t)与n(t)互不相关，且ω0>Bn，这一条件通常可以在中频信号采样之后通过频谱搬移来实现。于是输入信号sin(t)的功率谱密度Pin(ω)可表示为：

Pin(ω)=A2π/2[δ(ω-ω0)+δ(ω+ω0)]+

(2)

式中，n0表示噪声谱密度；δ(·)表示狄拉克函数。对sin(t)实施平方运算之后进行低通滤波，可得检波器的输出信号sout,sq(t)为：

(3)

式中，fliterL[·]表示截止频率为ωlow的低通滤波运算，且ωlow≤Bn。在理想低通滤波条件下，输出信号sout,sq(t)可以看成是一个广义平稳随机过程，其功率谱密度Pout(ω)为：

Pout(ω)=Paa(ω)+Pan(ω)+Pnn(ω)，

(4)

式中，Paa(ω)为信号自身相互作用产生的分量；Pan(ω)为信号与噪声相互作用产生的分量；Pnn(ω)为噪声之间相互作用产生的分量。当ωlow=Bn时，上述各分量分别表示为：

Paa(ω)=A4π/2·δ(ω)，

(5)

(6)

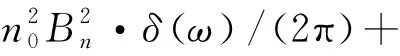
(7)

(a)本文的结果

2 基于希尔伯特变换的包络检波模型

一个实信号sin(t)对应的希尔伯特变换为：

(8)

式中，*表示卷积运算，于是该实信号sin(t)对应复值形式的解析信号zin(t)为[15]：

(9)

记实信号的sin(t)的频谱为Sin(ω)，则解析信号zin(t)对应的频谱Zin(ω)为：

(10)

于是该实信号sin(t)的包络envin(t)就是解析信号zin(t)的模值：

envin(t)=|zin(t)|。

(11)

在实际工程应用中可利用式(10)的性质，通过快速傅里叶变换(FFT)与逆变换(IFFT)来获得一个实信号所对应的解析信号，然后由信号的模值来求取该信号的包络，主要步骤如下：

① 对采样后的离散实信号x(n)进行FFT得到其频域信号X(k)，其中n,k∈{0,1,2,…,N-1}；

③ 对Y(k)做IFFT，即可得到离散实信号x(n)对应的复解析信号y(n)；

④ 复解析信号y(n)的模值|y(n)|即对应了离散实信号x(n)的包络。

3 2种检波方法的联系与性能分析

3.1 2种检波方法之间的联系

前面分别对平方率检波与基于希尔伯特变换的包络检波这2种工程上常用的典型方法进行了简要介绍。虽然它们在工程实现步骤上各不相同，但本质上它们之间的联系是非常紧密的，因为研究后发现，基于希尔伯特变换的包络检波是平方率包络检波的一个特例，详细解释如下。

雷达脉冲信号sa(t)对应的解析信号za(t)为：

zr(t)=A·exp[j(ω0t+θ)]，

(12)

高斯噪声n(t)对应的解析信号zn(t)为：

zn(t)=nc(t)cos(ω0t)+jns(t)sin(ω0t)，

(13)

式中，nc(t)，ns(t)分别为高斯噪声的同相与正交分量，该噪声信号的带宽为Bn。将zin(t)=zr(t)+zn(t)代入式(11)，即可求得输入信号sin(t)的包络envin(t)。在这一求模过程中自然去除了信号载频的影响，将结果与前面的式(3)对比后可以发现：当ωlow=Bn时有下式成立：

(14)

式中，β为一个比例系数。

由于平方率包络检波中低通滤波器的带宽ωlow(又称为视频带宽)可以随不同的应用，在ωlow≤Bn范围内进行调整取值，所以其检波结果也是随带宽ωlow不同取值而变化的。由式(14)可知，在ωlow=Bn，即在低通滤波器的带宽等于输入端的接收带宽(又称为射频带宽)时，平方率包络检波的结果与基于希尔伯特变换的包络检波结果的平方成正比。由此说明，基于希尔伯特变换的包络检波是平方率包络检波的一个特例。二者之间的关系可由图2形象地表示。

图2 2种检波器之间的关系Fig.2 Relationship between the two detectors

3.2 在ωlow=Bn情况下的性能分析

对平方率检波器中视频带宽与射频带宽相等，即ωlow=Bn，这一条件下的检波性能进行分析。显然，由前一小节的结论可知，该分析结果同样适用于基于希尔伯特变换的包络检波。

记检波器输入端信号的全频段功率信噪比为S/N|in,sq，即：

(15)

由于平方运算属于非线性变换，所以在输出的视频脉冲信号中将Paa(ω)看成是有效的信号分量；对于Pan(ω)来讲，只有在信号存在时才会出现，再考虑到式(6)与图1，将Pan(ω)中位于零频的冲激脉冲分量看成是有效信号分量，而将其他分量看成是噪声分量；对于Pnn(ω)来讲，其中位于零频的冲激脉冲分量无论是否有信号出现始终一直存在，所以在输出信噪比计算中不予考虑，而将Pnn(ω)中其他分量看成是噪声分量。于是输出端的信噪比S/N|out,sq可定义为视频带宽内信号分量与噪声分量的功率之比：

(16)

将式(5)～式(7)带入式(16)，并取ωlow=Bn，再对比式(15)，可得检波器的输出端信噪比与输入端信噪比之间的关系为：

(17)

由式(17)可知，当S/N|in,sq≫1时：

S/N|out,sq≈0.5·S/N|in,sq，

(18)

当S/N|in,sq≪1时：

S/N|out,sq≈2·S/N|in,sq。

(19)

由上可知，在ωlow=Bn条件下，当输入信号的全频段功率信噪比较高时，输出信号的信噪比相对于输入信号的信噪比大约恶化3 dB；当输入信号的全频段功率信噪比较低时，输出信号的信噪比相对于输入信号的信噪比大约提升3 dB。将式(17)的特性绘制于图3中(如实线所示)，图3中的虚线是输入与输出相等时的参考直线。为了便于展示，图3全部采用对数坐标，单位dB。由于平方率包络检波器在视频带宽与射频带宽相等时与基于希尔伯特变换的包络检波等价，此时由图3可见，在ωlow=Bn时二者的输入信噪比与输出信噪比之间差异并不大。

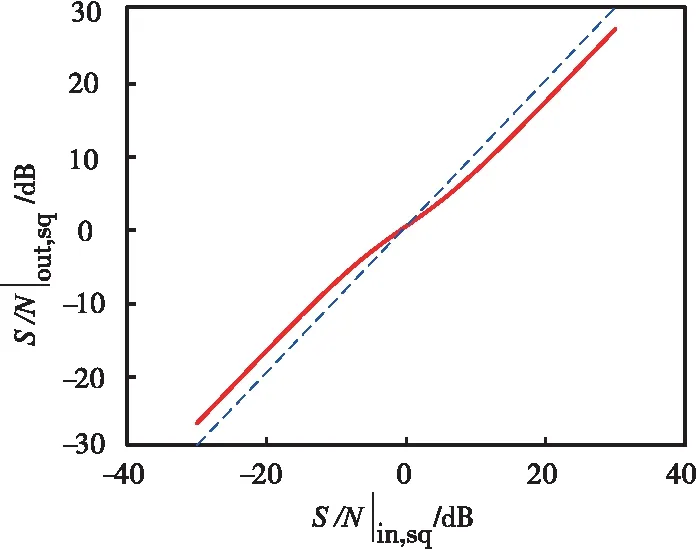
图3 ωlow=Bn时输出信噪比与输入信噪比之间的关系Fig.3 Relationship between output SNR and input SNRwhen ωlow=Bn

3.3 提升平方率检波器性能的方法

提升平方率检波器在较低的全频段功率信噪比条件下的性能，主要有2种方法：

① 减小平方率检波器的视频带宽

该方法等价于降低平方率检波器中的低通滤波器的截止频率ωlow，ωlow减小的下限等于信号带宽的一半，当ωlow=0.5Bs时，由式(16)可计算出检波器的输出信噪比S/N|out,sqwlow=0.5Bs：

(20)

式中，γ=Bn/Bs，表示检波器输入端射频带宽与信号带宽的比值，在γ≫1时式(20)可近似为：

(21)

对比式(21)与式(17)，并参照图1可知，相对于原来较宽的视频带宽来讲，其性能提升是非常明显的，即检波之后的信噪比提升了大约γ倍。

② 减少平方率检波器输入端的射频带宽

该方法等价于减小输入端的噪声带宽Bn，而Bn能够减小的下限等于脉冲信号的带宽Bs。由于信号的全频段功率信噪比S/N|in,sq与其带内功率信噪比S/N|in,sqinband之间的关系为[16]：

(22)

由式(22)可知，当Bn→Bs时，检波器输入端信号的全频段功率信噪比为S/N|in,sq将提升至信号的带内功率信噪比S/N|in,sqinband，提升的倍数同样为γ倍。在工程上实现检波器射频带宽减小的主要方法是信道化处理，将一个较宽的射频带宽划分成带宽更小的信道；另一方面，也可以采用在频域检测脉冲信号的载频与带宽等参数之后，再引导时域检波的方法来实现。

由上可见，从理论模型上讲，上述2种提升平方率检波器在较低的全频段信噪比条件下性能的方法，其效果近似一样。但是从工程实现的便捷性上讲，第1种方法优于第2种方法，因为无论是信道化还是频域检测后引导检波，都会增加侦察设备的软硬件复杂度，这也是第1种方法在工程上应用更加广泛的重要原因。

4 侦察灵敏度的计算

一般情况下，雷达侦察接收机的侦察灵敏度Pr,min是指满足侦察接收机对接收信号能量正常检测条件下，在侦察接收机输入端的最小信号功率。雷达侦察接收机通过平方率检波输出的最小信号功率与信噪比紧密相关，由前可知，这一信噪比与输入信号带宽Bs是紧密关联在一起的，即在不同信号带宽条件下，接收机的灵敏度也是不同的。所以在定义一个雷达侦察接收机的灵敏度Pr,min时，一定要明确指出对应的能够检测的信号带宽Bs的准确数值，否则将给设备使用方造成极大误解。

在检波器的视频输出端的脉冲叠加噪声之后输出信号的底部与仅有噪声时信号的顶部近似在一条直线上(相切)时，输出端的信噪比大约为8 dB，即S/N|out,sq≈8 dB。由式(22)可知，雷达侦察接收机要达到最高灵敏度需要包络检波器输入的射频带宽等于被检测信号的信号带宽；如果在此条件下即使包络检波器输出端的视频带宽也同样与射频带宽相同，即ωlow=Bn=Bs，此时的S/N|in,sq也应该是比较大的，于是由式(18)可知，检波器输入端的信噪比S/N|in,sq可表示为：

S/N|in,sq≈S/N|out,sq+3 dB=11 dB，

(23)

于是可计算出在此条件下，雷达侦察接收机的灵敏度Pr,min(单位：dBm)为：

Pr,min=-114+10lg(Bs)+Fr+S/N|in,sq=

-114+10lg(Bs)+Fr+11=

-103+10lg(Bs)+Fr，

(24)

式中，Fr表示侦察接收机的噪声系数，单位dB；信号带宽Bs的单位为MHz。由上可见，对于不同带宽的脉冲信号，雷达侦察接收机的最高灵敏度也是各不相同的。下面以噪声系数Fr=3 dB为例，根据式(24)计算出，在ωlow=Bn=Bs条件下，针对不同脉宽的雷达脉冲的侦察灵敏度如表1所示。这同时也是采用基于希尔伯特变换的包络检波的雷达侦察接收机所能达到的最高侦察灵敏度。由表1可见，同一部雷达侦察接收机在不同脉宽条件下，侦察灵敏度差异竟高达17 dB。

表1 在ωlow=Bn=Bs下不同脉冲信号的侦察灵敏度

另一方面，由式(20)可知，在上述检波的ωlow=Bn=Bs基础上通过进一步减少视频带宽，即ωlow=0.5Bs，还可以提升灵敏度，但提升的幅度极为有限，基本可以忽略。

5 仿真验证

以工程中最常见的脉宽1 μs单频脉冲信号为例对前述理论分析的结果进行仿真验证。该脉冲信号的载频设置为300 MHz，信号带宽Bs=1 MHz，输入平方率检波器的整个频率范围为275～475 MHz，这意味着Bn=200 MHz。在全频段功率信噪比S/N|in,sq= -2 dB条件下进行平方率包络检波，当检波器输出端的视频带宽ωlow=Bn时，经过50 000次蒙特卡洛仿真平均之后得到的信号功率谱如图4所示。

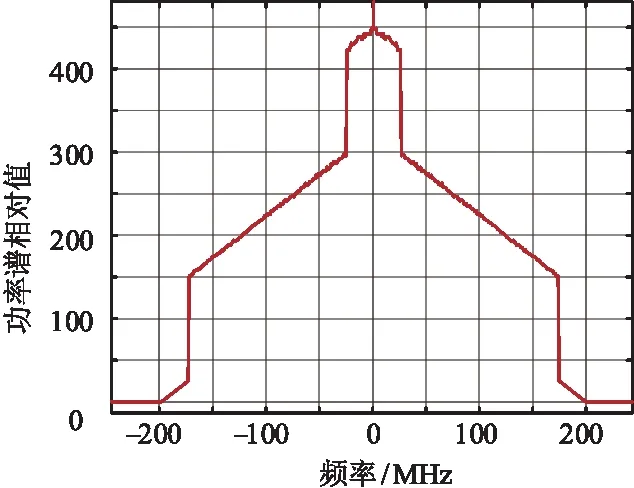
图4 平方率检波输出信号的功率谱密度仿真结果Fig.4 Simulation results of power spectral density forsquare rate detection output signal

与式(5)～式(7)的理论值比对，并对照图4与图1(a)可知，仿真结果与理论分析结果完全吻合，说明前述平方率检波理论模型构建的正确性。

为了验证平方率检波与基于希尔伯特变换的包络检波之间的联系，下面在切线灵敏度条件下用这2种检波方法对同一段信号进行检波，该段信号时长2 μs，其中0.5～1.5 μs为单频脉冲持续时间，脉冲信号载频仍然为300 MHz，即Bs=1 MHz，输入检波器的频率范围仍然为275～475 MHz，平方率检波器的视频端的接收带宽Bn相等，即ωlow=Bn=200 MHz。根据前面的理论分析，此时输入信号的全频段信噪比约11 dB，信号的时域波形如图5所示。

图5 检波前信号的时域波形Fig.5 Diagram of signal waveform in time domain before detection

对图5所示脉冲信号进行平方率检波，输出结果如图6(a)所示，采用基于希尔伯特变换的包络检波的输出结果如图6(b)所示(对信号模值进行平方处理之后绘制于图6(b)中)。

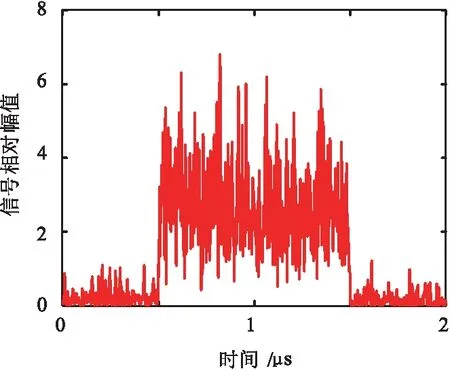
(a)平方率检波

由图6可知，在ωlow=Bn=200 MHz条件下，2种脉冲包络检波结果是完全相同的，这与前面式(14)的理论分析结果也是完全吻合的，即基于希尔伯特变换的包络检波是平方率包络检波的一个特例。

为了进一步提高检波灵敏度，可在此基础上，进一步缩减平方率检波器的视频带宽ωlow至10 MHz，虽然此时检波器的视频带宽ωlow是信号带宽Bs的10倍，但是射频带宽Bn是信号带宽Bs的200倍，参照式(21)可近似认为相对于图6中检波结果信噪比提升了13 dB，其检波结果如图7所示，与图6对比，其信噪比提升是十分明显的。

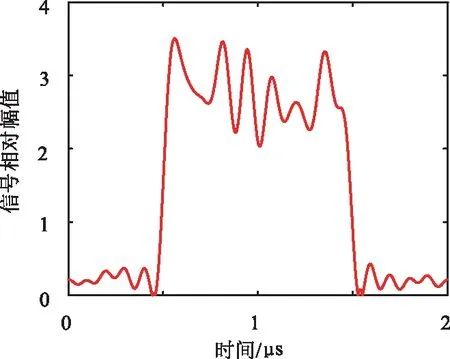
图7 在缩减视频带宽时平方率检波的输出结果Fig.7 Output of square rate detection when videobandwidth is reduced

6 结束语

在经典的雷达对抗教科书与传统的雷达信号检测文献中大多以二极管模拟检波器为例来构建并阐释平方率检波器的数学模型与雷达侦察接收机的灵敏度计算公式。但随着宽带高速数字信号处理技术的发展，数字检波器的应用越来越普遍。本文对中频数字平方率检波与基于希尔伯特变换的包络检波这2种工程中常用的典型脉冲数字信号包络提取方法之间的联系与性能进行了分析，指出了基于希尔伯特变换的包络检波是平方率包络检波的一个特例，分析了在提升平方率检波器性能过程中输入信噪比与输出信噪比之间的定量关系。在此基础上，利用上述结果对雷达侦察数字接收机的侦察灵敏度进行了计算，指出了在评估与度量雷达侦察接收机的灵敏度时，一定要明确声明对应的能够检测信号带宽的准确数值的必要性。以上分析结果是对传统雷达信号检测理论的扩展与补充，相对于传统理论来讲具有向后兼容性，也具有更广的普适性，这为雷达侦察数字接收机的方案论证、系统设计与指标分析提供了新的理论指导。