扩跳频测控系统中非相干测速技术的实现

李常青，许 利，罗 霞

(北京遥测技术研究所，北京 100076)

0 引言

无论是导弹测控还是航天器测控，测控系统均需要提供导弹或者航天器的精确测量结果。航天测控系统大多采用相干体制[1]来完成对航天器速度的测量，这种方法的优点是由于上下行频率相干，地面很容易测得双向多普勒；但是为了保证上下行信号紧密相干，应答机设计较为复杂，缺乏灵活性。而非相干测速技术[2]相对复杂，但是能很好地解决相干测速的缺点，并且当系统采用多站交会测量定位体制或链式接力测量方法时，非相干测速应答机能同时接收并转发多站地面信号，完成多站的精确定轨。文献[2]介绍了非相干测速的实现方法，并未对其测速精度进行研究。文献[3]单一地分析了相干测速系统中频率源不稳定造成的测速误差；文献[4]详细分析了电离层、对流层和多径等因素引入的测速误差，并给出了相应的修正方法和抑制策略，但2篇文献都是针对相干测速系统的，并没有提及非相干测速技术。本文首先提出了扩跳频测控系统中非相干测速的基本方法，该方法能克服因载波跳变带来的相位不连续[5]问题，分析了非相干测速技术中各个误差源引入的随机误差，并对其进行定量分析。结果表明，在一定条件下，非相干测控体制与相干测控体制的测速误差大致相当，满足工程指标要求。

1 非相干测速的基本原理

在航天测控领域，通常利用多普勒效应来测量航天器的速度，要得到准确的速度值就需要准确地测量载波的多普勒[6-7]。扩跳频信号体制的速度测量采用双向测多普勒的方式实现，非相干测速原理如图1所示。目标应答机利用自身形成的下行测量帧同步采样上行伪多普勒测量值，将采样信息实时写入下行测量帧并送回地面，地面设备使用恢复出的下行测量帧同步采样下行伪多普勒测量值，然后将上行单向伪多普勒值与下行单向伪多普勒值进行计算，从而得到目标的径向速度。要求星上伪多普勒测量积分时间和地面伪多普勒测量积分时间一致，星上采样时刻为下行测量帧同步时刻，地面采样时刻为接收到下行测量帧同步时刻。

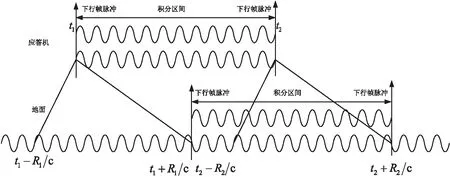
图1 非相干测速原理Fig.1 Principle of non-coherent velocity measurement

在星上t1～t2积分时间段内，地面发出的上行信号载波相位增量应与星上测得的上行信号载波相位增量相等；同理，星上发出的下行信号载波相位增量与地面在该积分时间段内，测得的下行信号载波相位增量相等[8]，经整理可以得到：

(1)

由式(1)可知，星钟对测速无影响；同时，由于地面站采用原子钟作为系统频率参考，时钟短稳指标较高[9]，考虑到地面原子钟是测量系统频率的参考基准，可以认为σg为零。因此，理论上可以认为此时的测速误差与星上时钟无关，仅取决于载波环路的跟踪精度[10]和积分周期。

由上述分析可知，可将式(1)简化为：

(2)

从而，解得目标的径向速度为：

(3)

式中，c为光速。在扩跳频体制中采用了载波跳频方式，不同频点的多普勒频率不同，不同多普勒频率都可对应目标当前的速度测量值[11]，对这些速度测量值进行线性拟合即可得到目标的速度测量值。

2 非相干测速具体流程

非相干测速技术流程如图2所示。

图2 非相干测速技术框图Fig.2 Block diagram of non-coherent velocity measurement technology

由图2可以看出，地面设备首先根据实时跟踪的载波相位积分求平均获得下行接收信号的平均伪多普勒信息，同时从上行测量帧中提取应答机下发的上行伪速度信息，换算成上行伪多普勒信息后，根据速度解算公式解算出目标的伪速度。

地面下行伪多普勒的计算步骤如下：

① 计算接收信号每一跳的总载波相位值。根据载波跟踪锁相环得到的载波实时相位值，在每一跳起始时刻，记录当前跳的初始相位和上一跳的结束相位，以及每一跳载波相位溢出次数和总累加次数；根据溢出次数、初始相位和结束相位计算出接收信号一跳的总相位：接收信号每跳总相位=溢出次数×2N+结束相位-初始相位，N为载波NCO的位数；

② 计算标准总相位。本地未加多普勒的每跳载波频率控制字可从地面设备中直接获取，根据总累加次数和本地未加多普勒的每跳载波频率控制字，计算出每跳标准总相位：每跳标准总相位=累加次数×载波频率控制字；

③ 计算每跳总下行多普勒相位。每跳总下行多普勒相位=接收信号每跳总相位-每跳标准总相位；

④ 每跳总下行伪多普勒相位归一化至中心频率点。获取地面接收机中心频率点为f0，各跳频率点为f1+fi×n，其中fi为跳频间隔，n为跳频点号，f1为第一跳的载波频率，归一化公式为：

(4)

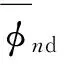
⑤ 将一帧内每一跳的归一化伪多普勒相位累加和再进行累加，同时将每一跳的累加次数再进行累加得到一帧内总累加次数；

⑥ 一帧内归一化伪多普勒相位累加和除以总累加次数，可求得一帧内的平均伪多普勒NCO值；

⑦ 将平均多普勒NCO值换算成平均伪多普勒测量值，计算公式：

(5)

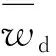
根据上述步骤，地面设备可计算出下行平均伪多普勒测量值，再提取应答机发送的下行测量帧中的上行伪速度信息，换算成上行伪多普勒测量值，进行速度解算。地面设备测速流程如图3所示。

图3 地面设备测速流程Fig.3 Velocity measurement process of ground equipment

3 星地测速系统的误差分析

在非相干测速系统中，误差来源主要为星地测量设备引入的误差、电波大气折射引入的误差以及测量原理引入的误差。其中，星地测量设备引入的随机误差占主要部分。下面对设备引入的主要误差进行分析。

3.1 热噪声抖动产生的误差

地面接收机采用Costas环实现载波跟踪，在实际工程中，Costas环不可避免地受到噪声的干扰，导致跟踪环路的性能降低，使环路的输出相位产生抖动。由热噪声引起的跟踪环抖动[12]为：

(6)

式中，C/N0为跟踪信号的输入载噪比；BL为载波环路的等效噪声带宽；fid为载波环路的积分清洗率；α为解扩损失因子(一般可取0.6)。

由接收机热噪声引入的测速误差为：

(7)

综上所述，环路热噪声误差取决于信号质量、载波环路相关参数的选取。

在C/N0=40 dBHz的条件下，取载波频率2.25 GHz，载波波长λ=0.14 m，积分时间τ=1 s，载波环路带宽取500 Hz，载波环路的积分清洗率fid取2 kHz，解扩损失因子α可取0.5(3 dB)，计算可得，在该条件下热噪声带来的测速误差δν为0.8 cm/s。

3.2 信道误差

信道引入测速误差[13]的主要来源是本振信号的抖动[14-15]和电源干扰及杂波干扰。

本振信号的相位抖动杂散与使用的频率参考源的短稳性能有关。频标信号的短期频率稳定度σ(20 ms)≤1×10-11，二阶载波环环路带宽为500 Hz，阿仑偏差引入的相位颤动为：

(8)

取信号载波频率2.25 GHz，载波波长λ=0.14 m，积分时间τ=1 s，可得到本振信号抖动带入的测速误差：

(9)

假设下行信道电源干扰及杂波功率总和与载波功率之比为-70 dBc/Hz，等效为：

σφ=10-70/20=0.000 3 rad。

(10)

取信号载波频率2.2 GHz，载波波长λ=0.14 m，积分时间τ= 0.5 s，可得到电源干扰及杂波干扰引入的测速误差：

(11)

上述2项测速误差合计为0.008 cm/s。

3.3 测量量化误差

测速是从数字载波环的NCO提取频率字来完成多普勒频率测量，若频率NCO为40位，工作时钟100 MHz，则地面设备多普勒量化误差[16]为：

σφ=2π×1×108/240=0.000 57 rad 。

(12)

取信号载波频率2.25 GHz，载波波长λ=0.14 m，积分时间τ=1 s，则测速量化误差为：

(13)

3.4 测速总误差

由上述分析可知，系统中测速误差的主要来源为环路热噪声引入的均方根跟踪抖动带来的随机误差。在一定条件下，非相干测控系统的测速精度与相干测控系统的测速精度相当。

4 数据分析

采用Simulink搭建的COSTAS环路验证上述分析的准确性，环路模型如图4所示。

图4 非相干测速技术中的COSTAS环模型Fig.4 COSTAS loop model for non-coherent velocity measurement

对载波跟踪模型进行参数设置，进行环路锁定时间仿真，环路跟踪曲线如图5所示。从图5的仿真结果可以看出，在高动态环境下，环路锁定时间短[10]，载波测量精度高。

图5 环路跟踪曲线Fig.5 Loop tracking curve

为了测试设备的可靠性，进行了非相干测速系统的外场测试。测试系统的信息速率为1 kb/s，伪码速率为5 Mb/s，信号调制方式为BPSK，载波环带宽设置在100 Hz，码环带宽设置为20 Hz，多普勒动态范围±10 kHz，多普勒变化率±5 Hz/s，上行频点为2 104.14 MHz，下行频点为2 285.04 MHz。共进行了2个系统的测试工作，每个系统分别做了5次测试，每次测试选用的积分时间为0.5 s，对每个频点进行测试时，取长度为1 min(120个点)数据进行分析。非相干测速系统实测速度如图6所示。

图6 非相干测速系统实测速度Fig.6 Measured velocity of non-coherent velocity measurement system

2个系统的实测速度值均方差如图7所示。不难看出，非相干测速系统的测速误差与相干测速系统的测速误差大致相当，其测速精度达到10-3m/s，满足工程应用的指标要求。相比传统的相干测速方法，非相干测速系统以其结构紧凑、功耗低，不需要进行相关处理而受到关注。因此，非相干测速技术具有一定的应用价值。

图7 2个系统的实测速度值均方差Fig.7 Mean square deviation of measured velocity of two systems

5 结束语

速度的测量对于航天器跟踪测量至关重要，由于采用了非相干测控体制，上下行信号无需相干，省去了很多相关处理的设计，使得应答机结构紧密、功耗低，其工程实现有一定的应用价值。本文介绍了非相干测速技术的基本原理，分析了影响测速精度的主要因素，并对其进行了定量计算。由实测数据分析可知，非相干测控体制和相干测控体制的测速误差基本相当。因此，非相干测速技术的研究具有理论研究价值与实际应用潜力。