基于数学形态学的密集转发干扰抑制算法

方 文，全英汇，陈侠达，董淑仙，高 霞

(西安电子科技大学 电子工程学院，陕西 西安 710071)

0 引言

数字射频存储器(Digital Radio Frequency Memory，DRFM)具有高速采样和复制宽带雷达信号的能力，基于DRFM的干扰机可以快速分析被拦截雷达信号的参数，快速产生与发射信号高度相关的干扰信号，并在当前脉冲重复周期内进行重复转发，因此，目标信号可能在时域和频域都与干扰信号重叠，使得雷达系统无法搜索或跟踪真实目标[1-7]。针对此问题，国内外学者提出了多种解决方法[8-15]，文献[11]提出了广义旁瓣相消器方法，来应对密集假目标干扰，这种方法可以有效抑制从天线旁瓣进入的虚假目标信号，但对于从天线主瓣进入的假目标，该方法不能有效抑制。文献[13]提出了脉冲重复周期捷变结合空间测角聚类以及空域滤波的方法对抗密集假目标干扰。文献[14]提出采用脉冲分集技术对抗重复转发干扰，该方法假设干扰机转发的干扰信号为雷达之前几个脉冲重复周期的发射波形。如果干扰机采取的干扰策略为转发雷达当前脉冲重复周期的发射信号，则此方法的抗干扰性能可能会降低。

针对上述问题，提出采用形态学滤波的方法对抗密集假目标干扰，该方法先采用最大类间方差(Otsu)算法计算脉压后数据空间的最佳阈值，对数据空间进行二值化处理。由于密集假目标干扰的距离和多普勒是失配的，在二值化后干扰为散乱分布的点，而目标的距离和多普勒是匹配的，目标轨迹为连续明亮的直线，根据这一特性，采用形态学中的开运算滤除干扰信号并且保留目标信号，对滤除干扰的回波信号，采用动目标检测(MTD)进行相参积累同时提取目标的速度信息。仿真实验和外场实测数据处理结果表明，文中所提算法能够有效抑制密集假目标干扰，提高脉冲多普勒雷达的抗干扰性能。

1 回波信号与干扰模型

1.1 回波信号模型

线性调频信号是一种广泛应用的大时宽带宽信号，假设雷达发射信号为线性调频(LFM)信号，在一个相参处理间隔内发射N个脉冲，则第n个脉冲发射信号的表达式为：

exp(j2πf0(t-nTr))，

(1)

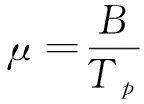
假设观测场景内存在一个与雷达的距离为R0，径向速度为v0的点目标，则第n个脉冲的回波信号为：

exp(jπμ(t-nTr-τ)2)exp(j2πf0(t-nTr-τ))，

(2)

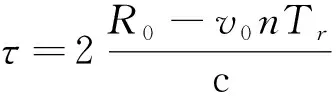
1.2 干扰信号模型

密集假目标干扰为干扰机在侦察截获到雷达发射信号后，对截获信号进行随机时延而不进行多普勒调制，然后迅速转发大量干扰信号，且覆盖整个脉冲重复周期。假设在一个脉冲重复周期内共有M个假目标，第m个假目标干扰信号的表达式为：

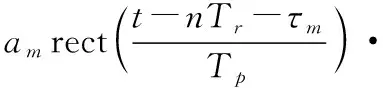
exp(jπμ(t-nTr-τm)2)·

exp(j2πf0(t-nTr-τm))，

(3)

式中，am，τm分别为第m个假目标的幅值和回波时延。则接收机接收到的第n个脉冲回波信号为：

S1(t,n)=sr(t,n)+sJ(t,n)+s1(t,n)，

(4)

式中，s1(t,n)为回波信号中的噪声。经匹配滤波后第n个脉冲回波信号为：

S2(t,n)=a′0sinc(πμTp(t-τ))exp(-j2πf0τ)+

(5)

式中，a′0，a′m分别为经匹配滤波后目标和干扰信号的幅值，且通常a′m≫a′0；s2(t,n)为匹配滤波后信号中的噪声。

由于转发干扰信号与发射信号具有较好的相关性，且干扰信号的功率远远大于目标回波信号，干扰信号不进行多普勒调制在进行相参积累时使得干扰信号的能量分布整个距离—速度二维平面，淹没了目标回波信号，致使雷达不能正常检测目标。因此，提出了利用数学形态学中的开运算抑制干扰信号，保证雷达在密集假目标干扰背景下可以检测目标。

2 基于数学形态学的密集干扰抑制算法

2.1 Otsu算法

Otsu算法是一种以类间方差最大化为准则的图像阈值分割算法[16-17]。本文利用Otsu算法计算最佳阈值，并将脉压后的回波数据进行二值化处理，抑制回波中的噪声，同时实现目标和干扰的提取。具体算法流程如下：

(1) 将脉压后的回波数据S2(t,n)按照脉冲数排列成二维平面，则平面大小为N×K，N表示脉冲数，K表示距离单元数。将第n个回波脉冲、第k个距离单元的幅值记为T(n,k)，并按照二维平面单元幅值大小分为L个区间，则N×K个单元中落入第l个区间的个数为al，并取区间中值Tl作为该区间的量化值。则各个区间量化值Tl发生的概率p(Tl)为：

(6)

(2) 选取阈值λ，用阈值λ可以将L个区间分为2个集合X，Y，则集合X={l|Tl<λ}，集合Y={l|Tl>λ}，则集合X，Y发生的概率分别为pX，pY：

(7)

(8)

利用式(6)～式(8)可以求得集合X，Y的平均幅值分别为avgX，avgY，以及总的平均幅值avg：

(9)

(10)

(11)

(3) 定义集合X，Y的类间方差为σ(λ)：

σ(λ)=pX(avg-avgX)2+pY(avg-avgY)2，

(12)

则最优阈值λ*为：

(13)

式中，集合T={T1,T2,…,TL}。

(4) 最后利用式(13)得到的最优阈值λ*将脉压后的数据二值化:

(14)

式中，T1(n,k)为阈值分割后第n个回波脉冲、第k个距离单元的幅值。

2.2 开运算抑制干扰

数学形态学(Mathematical Morphology)通过物体和结构元素相互作用的某些运算，获得物体的拓扑和结构信息[18-19]。形态学中的开运算为先腐蚀后膨胀，它可以剔除图像中一些较亮的斑点[20]。而脉压数据经过阈值分割后，干扰为一些亮的斑点，而目标为一条亮线，因此可以通过开运算剔除干扰，保留目标信息。开运算具体流程如下：

(1) 腐蚀运算

定义结构元为B，用B对二值化后的数据空间T1(n,k)做腐蚀运算：

T2(n,k)=(T1ΘB)(n,k)=

min{T1(n+n′,k+k′)-B(n′,k′)|(n′,k′)∈DB}，

(15)

式中，T2(n,k)为腐蚀后的数据空间；Θ表示腐蚀运算；DB为结构元的定义域。由于在数据空间中T1(n,k)干扰信号的邻域内存在噪声，而噪声在阈值分割时被置为零，因此经过腐蚀运算后干扰被置零。然而在数据空间中目标为一条连续的直线，经过腐蚀运算后目标信息得以保留。

(2) 膨胀运算

在进行上述腐蚀运算的过程中，目标周围经二值化处理后被置零的噪声会导致部分目标信息的丢失，表现为二值化处理后的数据空间中目标不再是一条连续的直线，而是多条间断的线段，因此需要通过膨胀运算将断续的目标连接起来。用结构元B对腐蚀后的数据空间T2(n,k)做膨胀运算：

T3(n,k)=(T2⊕B)(n,k)=

max{T1(n+n′,k+k′)+B(n′,k′)|(n′,k′)∈DB}，

(16)

式中，T3(n,k)为膨胀后的数据空间；⊕表示膨胀运算；DB为结构元的定义域。从式(16)可以看出，膨胀运算不会对已经置零的干扰和噪声产生影响，然而可以将丢失的部分目标信息恢复。

将经过开运算后的数据空间T3(n,k)与脉压结果S2(t,n)相乘，得到滤除干扰和噪声的脉压结果S3(t,n)：

S3(t,n)=T3(n,k)·S2(t,n)=

a′0sinc(πμTp(t-τ))exp(-j2πf0τ)=

(17)

最后对滤除干扰和噪声的脉压结果S3(t,n)利用快速傅里叶变换进行脉间相参积累，同时可以提取目标的速度信息。

3 仿真结果及分析

下面通过仿真验证所提方法的有效性。假设回波信号中干信比JNR=30 dB，脉压后回波信号中的信噪比SNR=14 dB，仿真设置的雷达及目标参数如表1所示。

表1 雷达及目标参数Tab.1 Parameters of radar and target

根据表1所示参数得到下述仿真结果图，图1(a)为雷达受到密集假目标干扰后脉压结果图，图1(b)为脉压结果的俯视图，图1(c)为未抑制干扰信号直接对脉压数据进行MTD的结果图。由前面对干扰信号模型分析可知，由于干扰信号距离和速度是失配的，相邻脉冲之间干扰信号是不相干的，因此干扰信号的能量分散在整个距离—速度二维平面，而且从图1(c)未抑制干扰的MTD结果可见，目标被干扰信号的能量完全淹没。

(a)脉压结果

为了能够使雷达正常检测到目标，采用本文所提方法，仿真结果如图2所示。利用Otsu算法对图1(a)所示的脉压结果进行阈值分割得到二值化结果，如图2(a)所示，可以看出图中散乱分布的亮点即为假目标干扰，而规律运动的目标为图中的亮线。对二值化结果进行开运算得到如图2(b)所示的开运算结果图，并将开运算结果与脉压结果相乘得到滤除干扰和噪声且保留目标信号的结果图，如图2(c)所示，此时干扰和噪声被完全滤除，而大部分目标信息被保留。最后再对滤除干扰和噪声的脉压结果利用快速傅里叶变换实现动目标检测进行相干积累，同时获得目标的距离、速度信息，MTD结果如图2(d)所示。此时可以获得目标的距离和速度信息，并实现对目标的检测。由仿真结果可以看出，所提方法可以有效抑制密集假目标干扰，保证雷达对目标的检测。下面分析该方法在不同干信比条件下目标检测性能。

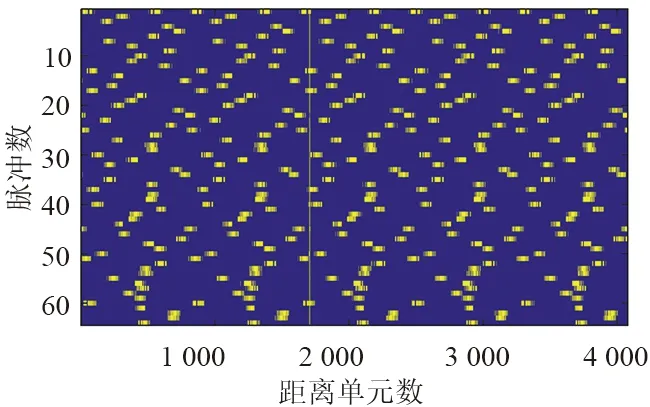
(a)二值化结果

为了分析文中所提算法的抗干扰性能，假设脉压后回波信号中的信噪比SNR=14 dB，接收机接收到回波信号中JSR从0 dB变化到70 dB，进行1 000次蒙特卡洛实验，得到如图3所示的检测概率随干信比变化的曲线。

可以看出，当JSR≤35 dB时，检测概率大于90%，此时所提算法能有效抑制密集假目标干扰。当JSR≥45 dB时，检测概率降低至0，这是由于干扰抑制后的回波信号中存在较强的干扰旁瓣，脉间相参积累后，能量较强的干扰旁瓣淹没了真实目标。

图3 检测概率随干信比变化的仿真曲线Fig.3 Simulation curve of detection probability varied with jam-to-signal ratio

4 实测数据处理

下面通过处理外场实测的对抗数据，来进一步验证所提算法的有效性。外场对抗场景为雷达观测海面上舰船目标，同时舰船上安置有干扰机，干扰机截获雷达发射信号，然后重复转发密集假目标干扰信号。

实测数据脉压结果如图4所示。

(a)实测数据脉压结果

可以看出，干扰信号散乱地分布在距离维，且干扰信号的能量在距离—速度二维平面覆盖真实目标，因而干扰机严重影响雷达正常检测目标。

未抑制干扰处理结果如图5所示。采用本文所提方法对实测数据进行处理，结果如图6所示。

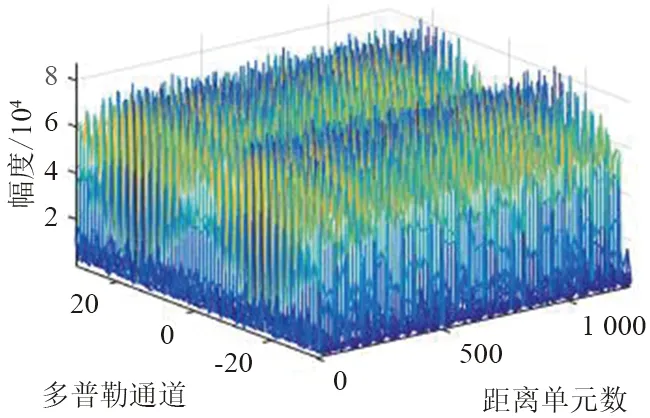
图5 未抑制干扰处理结果Fig.5 Processing result without suppressed interference

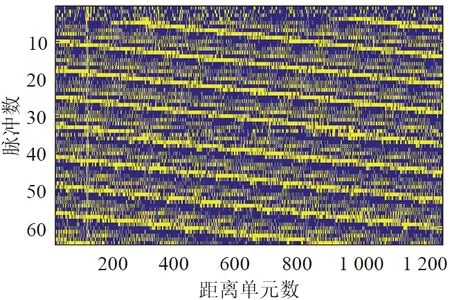
(a)实测数据二值化结果

对脉压数据采用Otsu算法计算最佳分割阈值，根据最佳阈值对脉压数据进行二值化处理，结果如图6(a)所示，可以看出此时噪声被尽可能地抑制而目标和干扰信号被保留下来，然后对二值化结果采用形态学开运算滤除密集假目标干扰信号，且保留大部分目标信息，结果如图6(b)所示。图6(c)为滤除假目标干扰信号后的结果，可以看出所提方法可以有效抑制密集假目标干扰并且极大保留了目标的信息。图6(d)为抑制干扰信号后MTD结果，可以计算出目标的距离和速度，以实现对目标的检测。对实测数据的处理验证了所提算法可以在强干扰背景下实现对目标的检测。

5 结束语

针对基于DRFM技术干扰机可以精确复制和重现雷达发射信号，然后重复转发，从而在真实目标之前和之后产生大量虚假目标，形成密集假目标干扰，导致雷达不能正常检测目标的问题，提出了基于数学形态学的密集假目标干扰抑制算法。该方法根据回波信号脉压数据采用大津算法计算噪声和真假目标之间的最佳分类阈值，抑制噪声同时保留目标和干扰信息，然后根据二值化后干扰为随机杂散分布的亮斑，而目标信号为连续的直线这一特点，利用形态学中的开运算滤除干扰信号，同时保留目标信息，达到了抗干扰的目的。仿真实验和外场实测数据的处理结果表明了基于数学形态学的密集假目标干扰抑制算法的有效性。