基于深度学习的含能材料生成焓预测方法
2021-02-03徐雅斌孙胜杰
徐雅斌,孙胜杰,武 装
(1. 北京信息科技大学计算机学院,北京 100101;2. 网络文化与数字传播北京市重点实验室,北京 100101;3. 北京材料基因工程高精尖创新中心北京信息科技大学,北京 100101)
1 引言
含能材料是一种在被加热激发后,不需要外界物质的参与即可通过自身的化学反应释放出能量的材料。作为炸药、火箭和导弹等推进剂配方的重要组分[1],在民用、国防、航天及空间站等领域已有广泛应用。如何提高能量始终是含能材料研究的一个主要目标和研究课题[2]。
在含能材料的研制过程中,生成焓是其能量性质的重要参数[3]。利用生成焓可以判断物质的相对稳定性、可以知道化学反应中的能量变化,这对于了解、控制和利用化学物质及化学反应是非常关键的。因此,获取含能材料的生成焓至关重要。目前,传统的含能材料生成焓获取方法,主要基于量子化学理论,使用高精度计算方法,如:原子化方法[4]、氧弹量热法[5]、等键反应方法[6]、半经验分子轨道理论(PM3)和分子力学(MM2)方法相结合的方法[7]等进行计算。但是这种方法需要首先利用密度泛函、Gess 定律、PM3 和MM2 等方法获取出计算生成焓的中间元素,之后再进行具体生成焓的计算。因此,在进行中间元素的计算时,不能保证计算的准确度,同时也会产生很大的计算量。
随着机器学习的不断发展,逐渐有人使用机器学习的方法对含能材料的生成焓进行预测。文献[8-10]中均采用人工神经网络分别对非芳香族多硝基化合物、芳香族多硝基化合物和高氮化合物的生成焓进行预测。Wan Zhong-yu 等[11]结合半经验(AM1)方法和分子描述符,使用多元逐步回归(MSR)方法对化合物的生 成 焓 进 行 预 测。DUAN Xue-mei 等[12]结 合Hartree-Fock/密度泛函理论(DFT)和线性回归方法来准确预测生成焓。Yalamanchi 等[13]将支持向量回归(SVR)方法和人工神经网络(ANN)方法进行对比,通过两次10 折交叉验证(10-fold CV)对三类无环和闭壳碳氢化合物的生成焓进行了预测,得到了性能更好的SVR 方法。以上文献均采用机器学习方法对含能材料的生成焓进行预测。但是,这种方法存在大量人工干预且特征提取复杂的问题。
利用深度学习方法对材料的性质进行预测的现象越来越多。闫海等[14]提出将卷积神经网络(CNN)应用于有限元代理模型,预测平面随机分布短纤维增强聚氨酯复合材料的有效弹性参数,并针对训练过程出现的过拟合问题,提出了一种数据增强的方法。宋新宽等[15]提出利用CNN 方法快速预测多孔材料内有效扩散系数,可根据多孔材料微观结构图直接预测有效扩散系数。胡石雄等[16]提出采用拼接的方法把一维数据转换成二维图像数据,然后使用一种Inception 结构作为CNN 的卷积层,另外使用全连接网络对提取特征进行补充,实现对热轧带钢的抗拉强度的预测。以上均采用单纯的CNN 进行性能预测,有效避免了复杂的人工干预和特征选取问题。但是,这种方法往往只专注于提取数据的深度特征,而忽略了数据之间的相关性。
晏臻等[17]提出CNN 和长短期记忆网络(LSTM)相结合的短时交通流量预测模型,通过CNN 挖掘相邻路口交通流量的空间关联性,通过LSTM 模型挖掘交通流量的时序特征,将提取的时空特征进行特征融合,实现短期流量预测。石文浩等[18]提出首先使用一维卷积神经网络(1D-CNN)来提取输入矩阵的局部特征,并抽象成全局特征,然后使用双向长短期记忆网络(Bi-LSTM)结合正反方向互补的信息,对miRNA-lncRNA 的互作关系进行预测。张鹏等[19]提出首先使用滑动窗口截取的方法获取数据,然后分别通过CNN 和LSTM 这两种模型分别得到特征向量,最后使用Attention 机制,将这两个特征向量融合成特征图,从而对QAR 数据中的飞机俯仰角进行预测。李梅等[20]针对时序数据特征,提出一种基于注意力机制的CNN 联合LSTM 的神经网络预测模型,融合粗细粒度特征实现准确的时间序列预测。
研究和分析发现,采用CNN 和LSTM 的融合模型虽然可以利用CNN 提取数据特征,又可以使用LSTM考虑数据之间的相关性,但是单向的LSTM 不能处理上下文数据对预测结果的影响,而双向LSTM 在性能优化方面有所欠缺。使用Attention 机制可以有效优化模型性能。
针对目前在材料性能预测方面存在的问题,本文提出一种基于Attention 机制的卷积神经网络(CNN)和双向长短期记忆神经网络(Bi-LSTM)融合模型对含能材料的生成焓进行预测。该模型以搜集和爬取到的含能材料分子结构的原子三维坐标为基础,首先对获取的坐标数据进行库仑矩阵的转换,数据的填充、截取和归一化;然后,利用CNN 提取数据中的深层特征;接下来,利用Bi-LSTM 考虑数据间的相关性;最后利用Attention 机制对特征的权重系数进行合理的优化,由此获得预测结果。
本文的主要内容如下:
(1)提出一种基于CNN 与Bi-LSTM 的融合模型,对含能材料的生成焓进行预测,既可以全面克服数据特征提取的困难,又可以充分考虑数据间的相关性,有效实现“结构—性能”的预测目标。
(2)针对无法对含能材料特征向量的重要程度进行合理评判的问题,使用Attention 机制对融合模型特征向量的权重进行计算,得出不同特征向量对预测结果的重要程度,从而提高含能材料生成焓预测的准确度。
(3)为了避免含能材料分子的原子坐标受到平移、旋转、交换索引顺序等操作的影响,进而对生成焓的预测结果造成一定的误差,选择将原子坐标数据转换成表示分子内笛卡尔坐标系的库仑矩阵,从而保证每种含能材料分子均对应唯一的结构数据。
2 数据搜集与预处理
2.1 数据搜集
首先,通过查询国内外知名的含能材料期刊和杂志(如:《Journal of Energetic Materials》、《含能材料》、《火炸药学报》等),搜集有关含能材料的实验数据,并将这些数据保存下来。
由于本文的设计的目标是根据含能材料的分子结构预测出对应的生成焓数值,而文献中搜集到的数据并不包括这些材料的分子结构。因此,需要根据保存的“PubChem 数据库ID”在PubChem 数据库中批量爬取对应分子结构的原子三维坐标。
然而,在搜集数据的过程中发现,对于某些材料来说,在不同的文献中给出的生成焓数值是不一样的,这可能受限于当时的实验条件和测量精度。但是由于无法判断哪些文献给出的生成焓数值是正确的,因此无法直接用于模型的训练,需要通过高通量计算方法确定正确的生成焓数值。因为本文中要预测的性质属于热力学性质,原子体系也不大,所以选择使用专门的组合方法,即高斯(Gaussian)G4 方法。由此计算出在标准状态(298 K)下分子结构对应的生成焓数值,同时将生成焓的单位统一为kJ·mol-1。
2.2 库仑矩阵的转换
在数据的预处理阶段,必须考虑某些额外操作(例如:平移、旋转、交换索引顺序等)对分子结构坐标的影响,甚至可能会对生成焓的预测结果造成一定的误差。而库仑矩阵则是一种用来表示分子内笛卡尔坐标系集合与核电荷的矩阵。其中,对角元素可以看作是原子与其自身的相互作用,本质上是原子能与核电荷的多项式拟合,非对角线元素代表核之间的库仑排斥。同时,库仑矩阵不受原子的平移、旋转和交换索引顺序的影响,每种分子对应的库仑矩阵是固定不变的[21]。其转换公式为:

在进行训练之前,需要根据公式(1)将每个含能材料的三维坐标数据转换对应的库仑矩阵。以化合物1,3,5-三嗪(C3H3N3)为例,将其坐标数据转换为库仑矩阵后的实验数据,如表1 所示。表示为一个对称矩阵,其中第i行和第i列共同代表一个原子的数据。
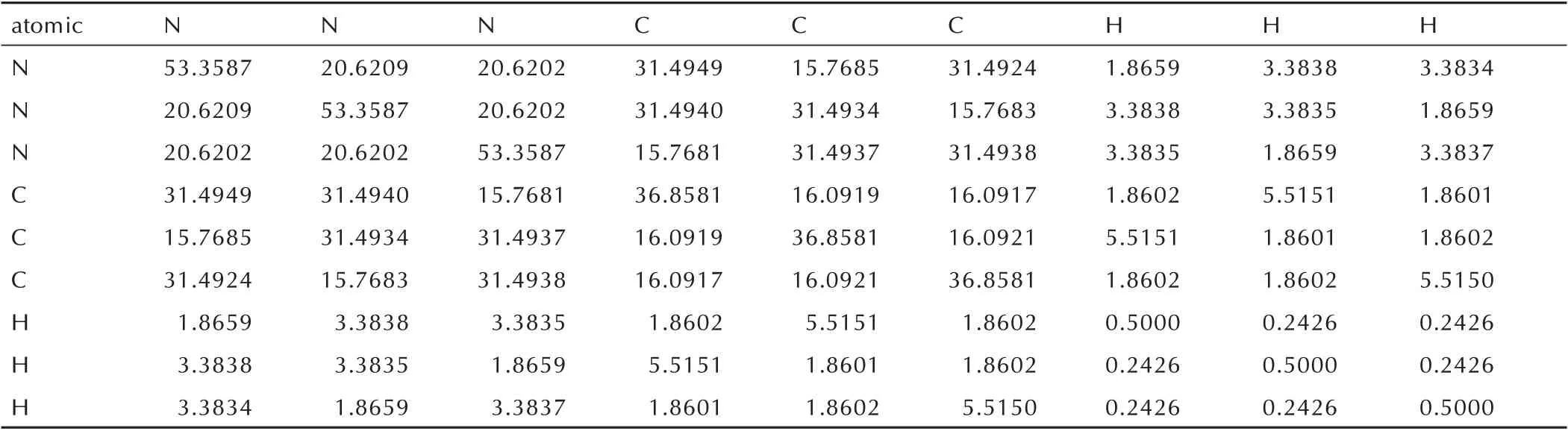
表1 转换为库仑矩阵后的实验数据Table 1 The experimental data converted to coulomb matrix. au
2.3 数据的填充、截取与归一化处理
对数据进行分析发现,每种材料分子中的原子数量是不一致的,材料分子中原子数量的分布情况如图1 所示。
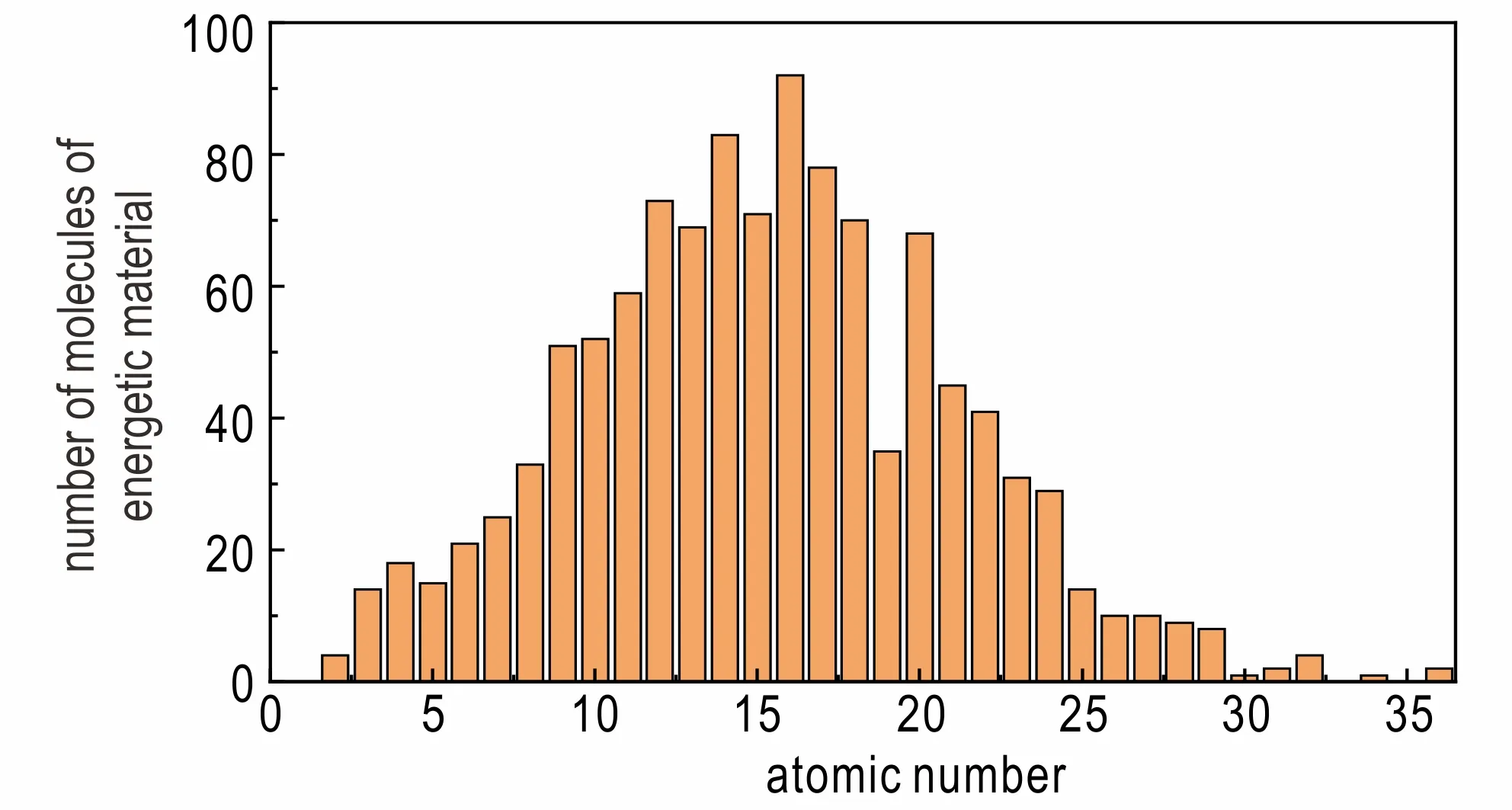
图1 材料分子中原子数量的分布情况Fig.1 The distribution of the number of atoms in the material molecule
由图1 可以看出,分子数量较多的原子数量主要集中在6~24,而在这批数据集中,原子数量的最大值和中位数均为16 个。因此,在将原子坐标转换成库仑矩阵之前,将原子数量为6~16 的原子坐标进行补0,填充到16 个原子坐标;而对原子数量为16~24 的原子坐标,则进行数据的截取。由于生成焓数值的大小主要依据材料分子中N—N 键、N—C 键、N=N 键和N#N 键等化学键的个数,即C 原子和N 原子的多少和位置。因此,在进行数据的截取时,选择只删除H 原子对应的库仑矩阵信息。
之后,为了消除奇异样本数据导致的不良影响,使得数据被限定在一定的范围内,使用max-min 归一化方法对转换成库仑矩阵之后的数据进行处理。其计算公式为:

其中,Xnorm为归一化后的数据,X为原始数据,Xmax、Xmin分别为原始数据集的最大值和最小值。
最后,将每条数据中经过归一化处理之后的库仑矩阵作为模型的输入向量。
3 模型设计
3.1 模型结构
针对含能材料分子结构中存在的特征不明显、提取难度大的问题,以及分子结构间的相关性难以考虑和分析的问题,我们提出一种基于Attention 机制的CNN 和Bi-LSTM 融合模型实现生成焓预测。模型的结构如图2 所示,主要分为输入层、卷积神经网络(CNN)层、Bi-LSTM 层、Attention 层、全连接层和输出层。
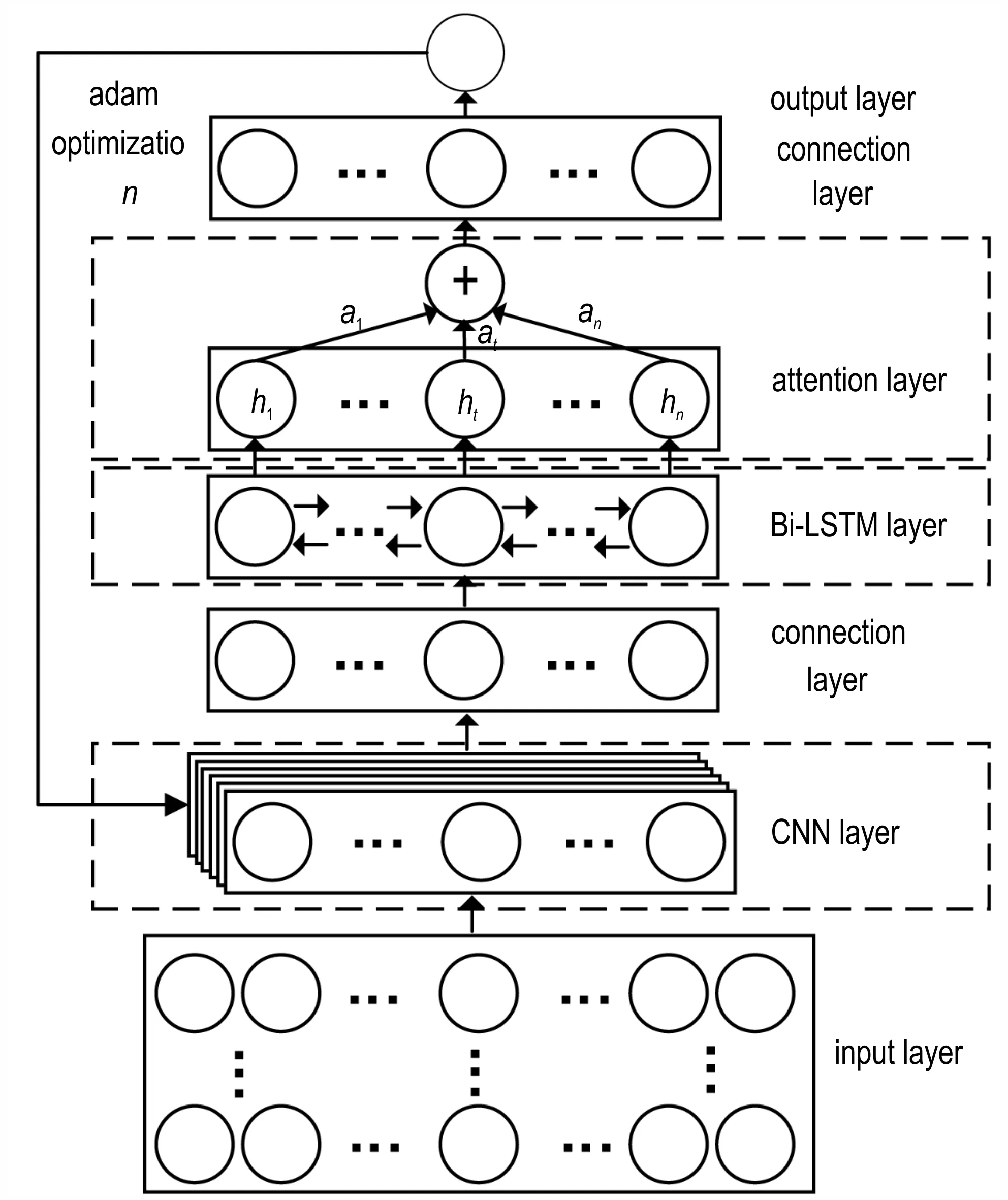
图2 生成焓预测模型架构Fig.2 Enthalpy of formation prediction model architecture
3.2 卷积神经网络(CNN)层
在进行含能材料生成焓预测时,选择含能材料分子结构即原子三维坐标转换成的库仑矩阵作为模型的输入数据,实际上就是依靠材料分子的库仑矩阵判断出各种原子键是否存在以及数量的多少,也就是数据中的特征。然而,这种数据存在特征不明显、提取难度大的问题。因此,为了充分提取出数据中的特征,我们首先使用CNN 对含能材料的数据进行特征提取。CNN 是一种通过卷积操作提取特征,再利用池化层学习数据局部特征的前馈神经网络。无需对输入数据进行大量预处理,即可以学习到大量的特征信息。本文中的卷积层采用四层卷积的形式,为了防止数据的过拟合,在卷积层中添加一个Dropout 层。由于Re-LU 函数具有便于稀疏化及有效减少梯度似然值的优势,故卷积层的激活函数选用ReLU 函数。

3.3 双向长短期记忆神经网络(Bi-LSTM)层
Bi-LSTM 是对LSTM 的一种改 进,由前向LSTM 和后向LSTM 组合而成,可以有效地考虑前后数据之间的相关性。
在含能材料分子结构数据中,包括两个方面的相关性:
(1)在含能材料的分子结构中,N—N 键、N—C键、N=N 键和N#N 键等化学键是生成焓主要的能量来源。而在输入数据即材料分子的库仑矩阵中,这些化学键是否存在以及数量的多少恰恰取决于N 原子与C 原子数据之间的相关性。因此,在含能材料的分子结构数据中,每个原子数据之间的相关性是必须要考虑的。
(2)在进行含能材料生成焓的预测时,数据对应的分子结构之间的差距并不大,往往只是增加或减少几个原子或者改变几个原子的位置,从而对生成焓的大小造成一定的影响。因此,当我们想要预测一个分子结构对应的生成焓时,其余分子结构数据与对应的生成焓值会对本次预测结果起到一定的辅助作用。所以,分子结构数据之间的相关性是我们要考虑的另一个重要问题。
基于以上内容,在提取出数据特征之后,为了充分考虑数据间的相关性,选择使用Bi-LSTM 对提取出的特征进行深层学习。Bi-LSTM 结构如图3 所示:
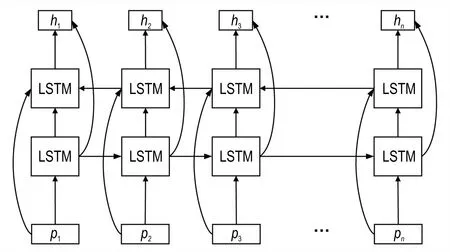
图3 Bi-LSTM 结构图Fig.3 Bi-LSTM structure
Bi-LSTM 层的输入数据即为CNN 层的输出数据P。Bi-LSTM 由 多 个LSTM 组 成,在 每 个LSTM 中 有 输入门i、遗忘门f、输出门o和记忆状态c,隐层状态ht的更新公式为:

其中,WI,WF,WO,WC,UI,UF,UO,UC均为相应的权重矩阵;bI,bF,bO,bC为偏置向量;σ,tanh 是激活函数;ht-1为上一时刻的隐藏状态,rt为临时记忆状态;⊙是按位乘运算。

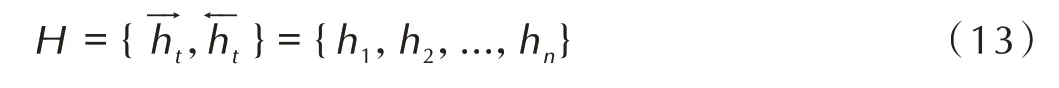
3.4 Attention 机制
Attention 机制是模仿人类注意力而提出的一种解决问题的办法。简单地说,就是从大量信息中快速筛选出高价值信息,通过利用高价值的信息提高计算的准确度。更进一步说,就是利用高价值信息解决计算资源的高效分配问题。
在本模型的设计中,为了提升预测结果的准确度,使用Attention 机制中的权重分配原则计算不同特征向量对应的权重值,使得越重要的特征所对应的注意力值越大,从而突出重要特征对预测结果的影响,提高预测结果的准确率。
Attention 机制层的输入数据即为Bi-LSTM 层的输出数据H。Attention 机制的结构如图4 所示:
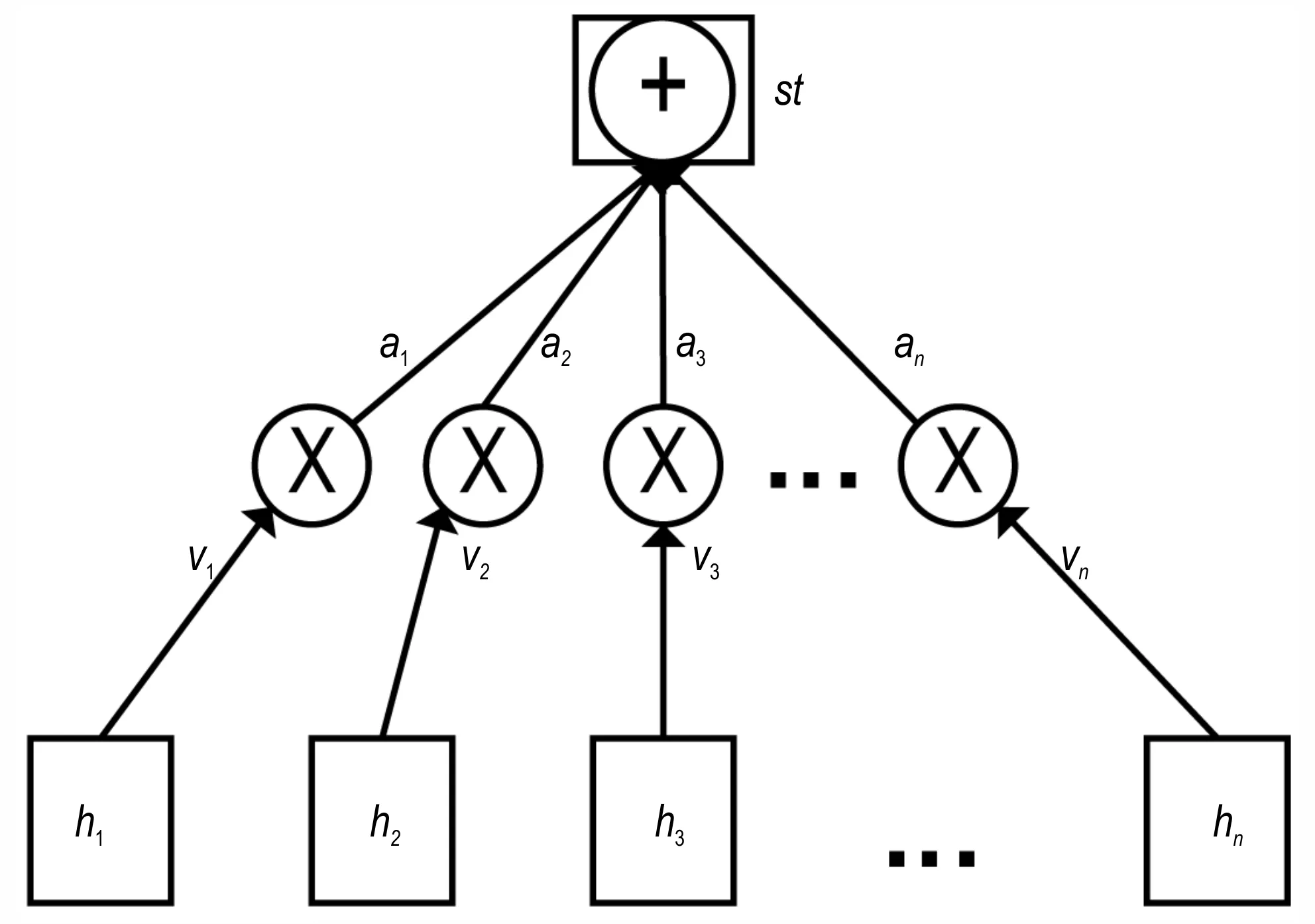
图4 Attention 机制结构图Fig.4 The structure of the Attention mechanism
首先,生成目标注意力权重vt;

其中,uv和wv均为权重系数,bv为偏置数,tanh 为激活函数。
其次,将注意力权重概率化,通过softmax 函数生成概率向量at;
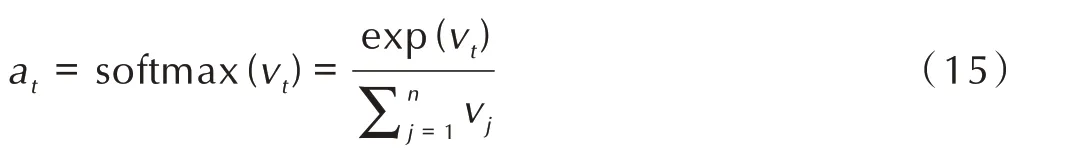
之后,进行注意力权重的配置,将生成的注意力权重配置给对应的隐层状态输出ht,使模型生成的注意力权重发挥作用,得到对隐层状态输出进行加权平均后的向量st。

最后,将向量st作为Attention 层的输出,并进入下一层。
3.5 全连接层
使用全连接层对Attention 机制的输出st进行计算,获得最终的预测结果y。在得到预测结果后,选用自适应优化算法(adaptive moment estimation,Adam)对模型参数进行优化。激活函数采用sigmoid 函数,最终的预测结果可表示为:

式中,wy为权重矩阵,by为偏置向量。
损失函数选择均方误差函数(Mean Squared Error,MSE),计算公式为:

该函数对于异常值(即预测值和实际值的误差远大于其他误差的数据点)更加敏感,平方和的计算结果会给异常值赋予更大的权重,模型会朝着减小异常值误差的方向更新。另外,该函数损失的梯度会随着损失的增大而增大,而损失趋于0 时则会减小。因此在训练结束时,该函数会更加稳定和精确。
4 结果与讨论
4.1 实验数据与实验环境
从3.1 中提到的国内外知名的含能材料期刊中进行数据的搜集,之后经过高斯(Gaussian)G4 计算和库仑矩阵转换等处理,最终共获得了1026 条可用数据。接下来,为了充分利用Bi-LSTM 提取出数据间的相关性,根据生成焓值的大小,对所有数据进行一次升序操作。最后,在进行模型的训练时,按照9∶1 的比例将数据集划分为训练集和测试集,之后利用10 折交叉验证将训练集再次划分成训练集和验证集。
实 验 环 境 为:CPU 型 号 为 Intel® Core ™i5-8259U CPU@2.3GHz,内存为16 GB,操作系统为macOS 10.15,开发语言为Python3,开发环境为PyCharm,数据库为MySQL。
4.2 评价指标
实验选取平均绝对误差MAE、平均绝对百分误差MAPE、均方根误差RMSE 和均方根对数误差RMSLE作为评价标准。四种指标越小,表明预测值越接近真实值,证明模型性能越好,特征表达能力越强。

4.3 参数优化实验
为了选择最优的批处理量(bitch_size),选择了6 种批处理量(4、8、12、16、20、24)分别进行10 折交叉验证。在相同的实验环境下,不同批处理量对应的平均绝对误差MAE 的情况如图5 所示。
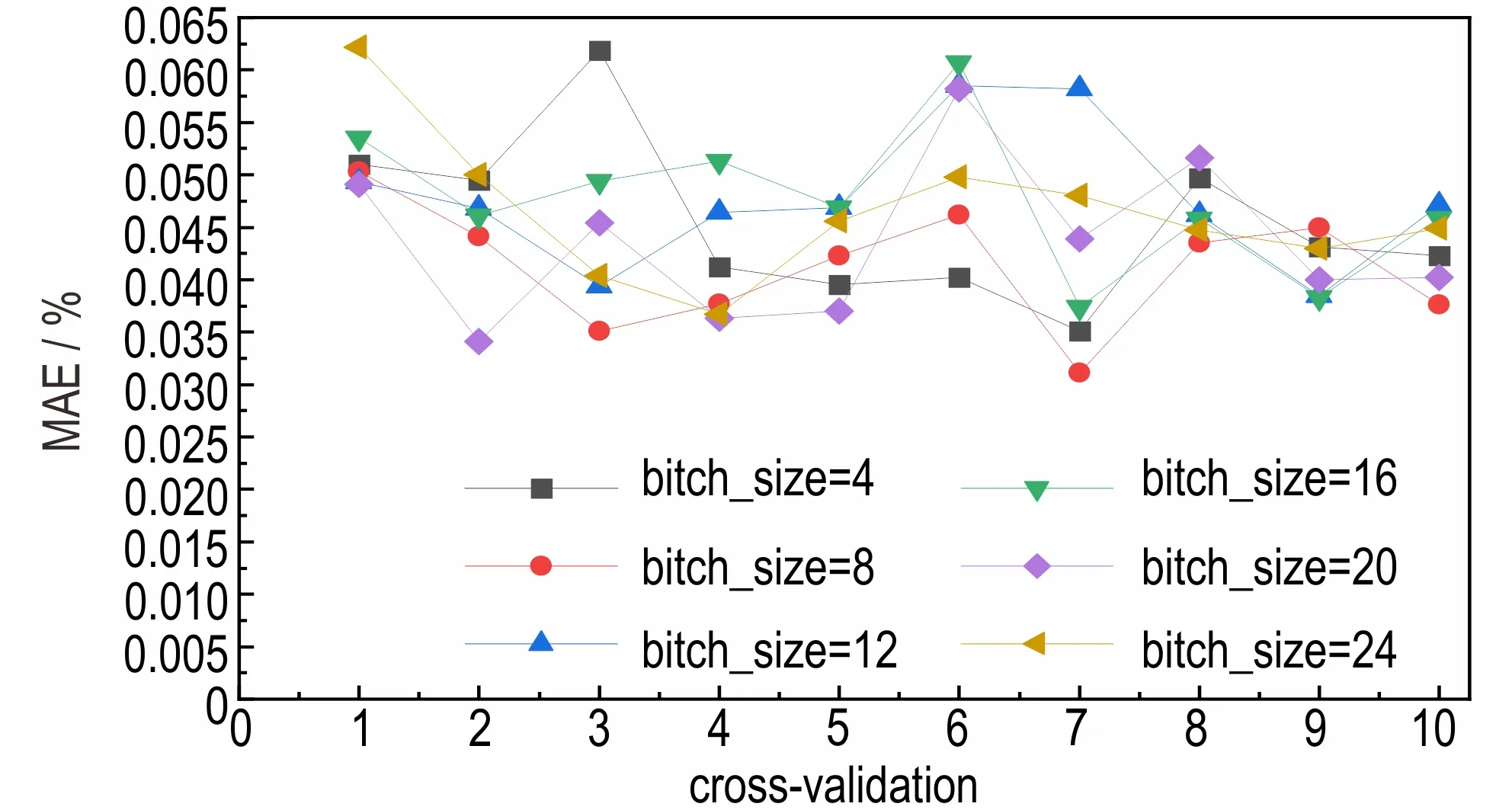
图5 不同批处理量对应的平均绝对误差Fig.5 Mean absolute error(MAE)corresponding to different batch throughput
从图5 中可以看出,当批处理量为8 时,具有最低的平均绝对误差MAE,因此选择本模型的批处理大小为8。
为了选择最优的训练轮次(epochs),使本模型具有较高的预测准确度,在相同的实验环境下,针对不用的训练轮次(25、50、75、100、125、150、175、200)进行实验,得到不同训练轮次下的生成焓预测效果(平均绝对误差MAE、平均绝对百分误差MAPE、均方根误差RMSE 和均方根对数误差EMSLE),实验结果如图6所示。
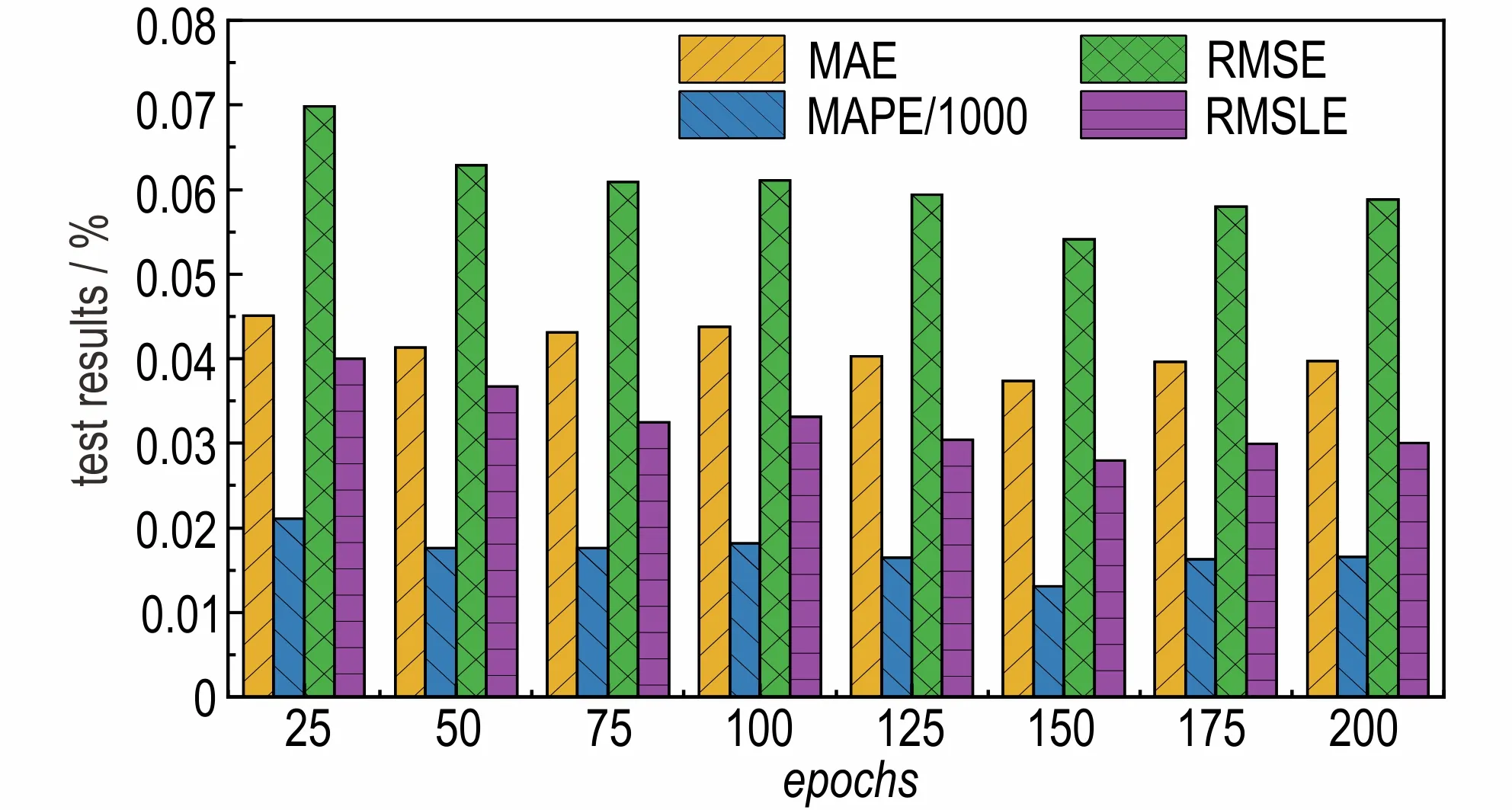
图6 不同训练轮次的预测效果Fig.6 Prediction effect of different training rounds 1)MAE is mean absolute error;2)MAPE/1000 is mean absolute percentage error/1000;3)RMSE is root mean square error;4)RMSLE is root mean squared logarithmic error.
从图6 可以看出,随着训练轮数的不断增大,平均绝对误差、平均绝对百分误差、均方根误差和均方根对数误差的值不断减小,并在训练轮次为150 的时候达到最小值,之后每个指标随着训练轮数的增加又开始不断增大。因此,当训练轮数为150 时,本模型的生成焓预测效果最好。
综上,获得最佳的批处理量(bitch_size)为8,最佳的训练轮数(epochs)为150。在此参数的基础上,利用测试集中的103 个数据对生成焓的真实值(y_true)和预测值(y_predict)进行对比,实验结果如图7 所示。
由图7 可以看出,此时测试集上生成焓的真实值和预测值的数据曲线较为拟合,说明此时模型参数已达到最优值,生成焓预测的效果最佳。
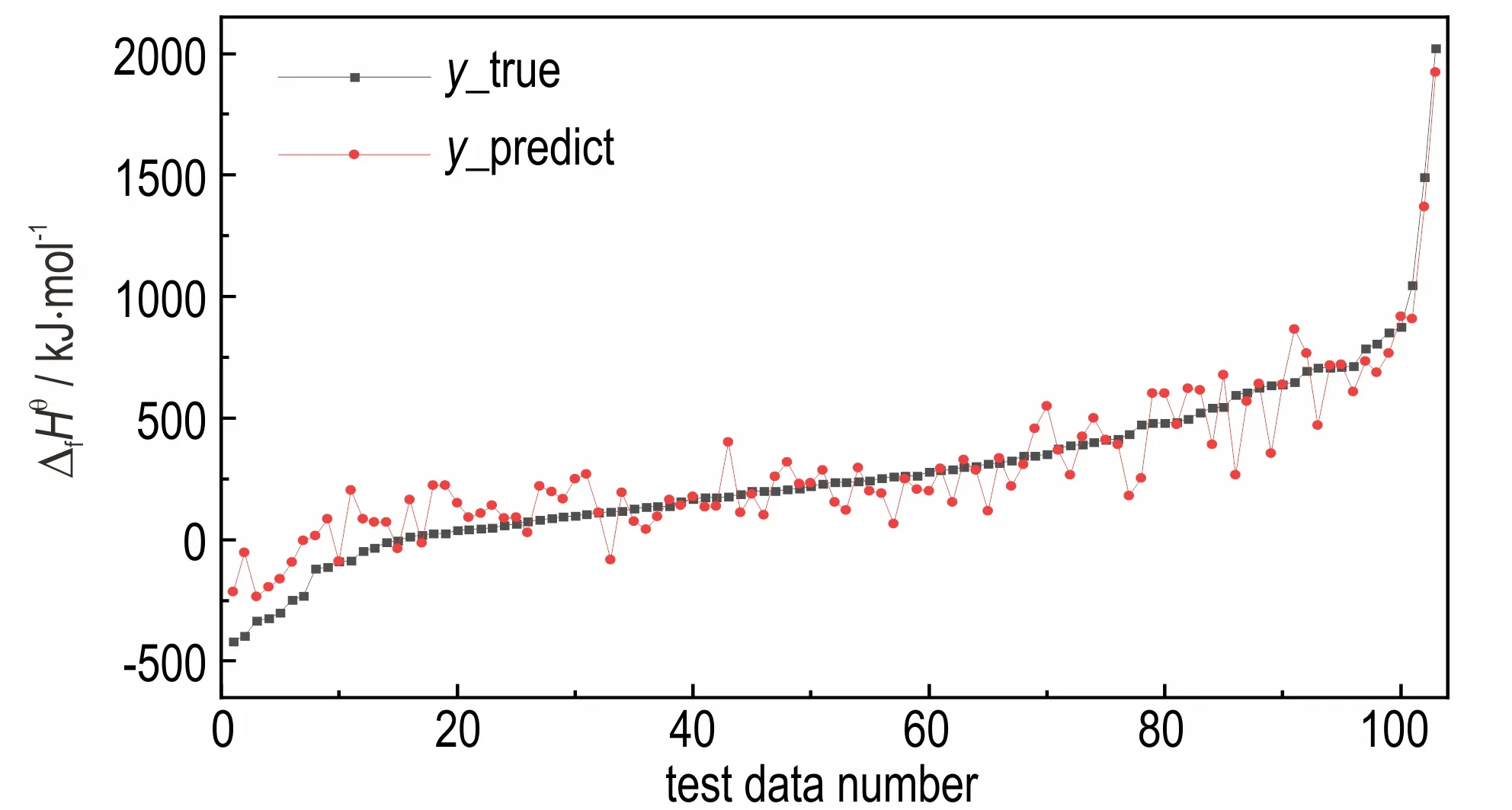
图7 最佳参数下测试集的预测效果图Fig.7 The prediction effect diagram of test set under the optimal parameter
4.4 对比实验
为验证本模型在含能材料生成焓预测的有效性和优势,利用本文数据集并采用10 折交叉验证方法,分别 将 文 献[13]、文 献[16]中 的 方 法 以 及CNN、Bi-LSTM、CNN-BiLSTM 方法和本文方法,在相同的实验环境下进行生成焓预测的对比实验,实验结果如图8 所示。
由图8 可以看出,文献[13]和文献[16]中使用的传统机器学习方法的实验误差更高,这两种方法的平均MAE、MAPE、RMSE 和RMSLE 分 别 为0.0554、2.44%、0.0755 和0.056。这是由于传统的机器学习方法对显性的数据特征有着很大的依赖性,需要使用更加具有代表性的数据特征才能获得更好的实验效果。然而本次实验的数据集是含能材料分子的库仑矩阵,并不能提取出显性的数据特征,导致其预测效果较差。
CNN 和Bi-LSTM 方法获得的实验误差相对较低,这两种方法的平均MAE、MAPE、RMSE 和RMSLE 分别为0.0496、2.05%、0.0719 和0.0375,并且Bi-LSTM 方法的实验误差低于CNN 方法。这是由于CNN 和Bi-LSTM 方法均可以提取出数据中的隐含特征,可以更好地对数据特征进行学习和训练。另外,Bi-LSTM方法还可以充分考虑含能材料分子库仑矩阵中数据之间的相关性,因而具有比CNN 更好的预测效果。
而CNN-BiLSTM 方法是CNN 和Bi-LSTM 的融合模型,可以同时拥有CNN 和Bi-LSTM 方法的优势,因而可以获得比两者更好的实验效果。最后,本方法在CNN-BiLSTM 方法的基础上,利用Attention 机制对特征向量的权重进行分配和优化,进而对不同特征向量的重要程度进行了合理的考虑。因此,采用本方法在对含能材料的生成焓进行预测具有非常明显的优势。
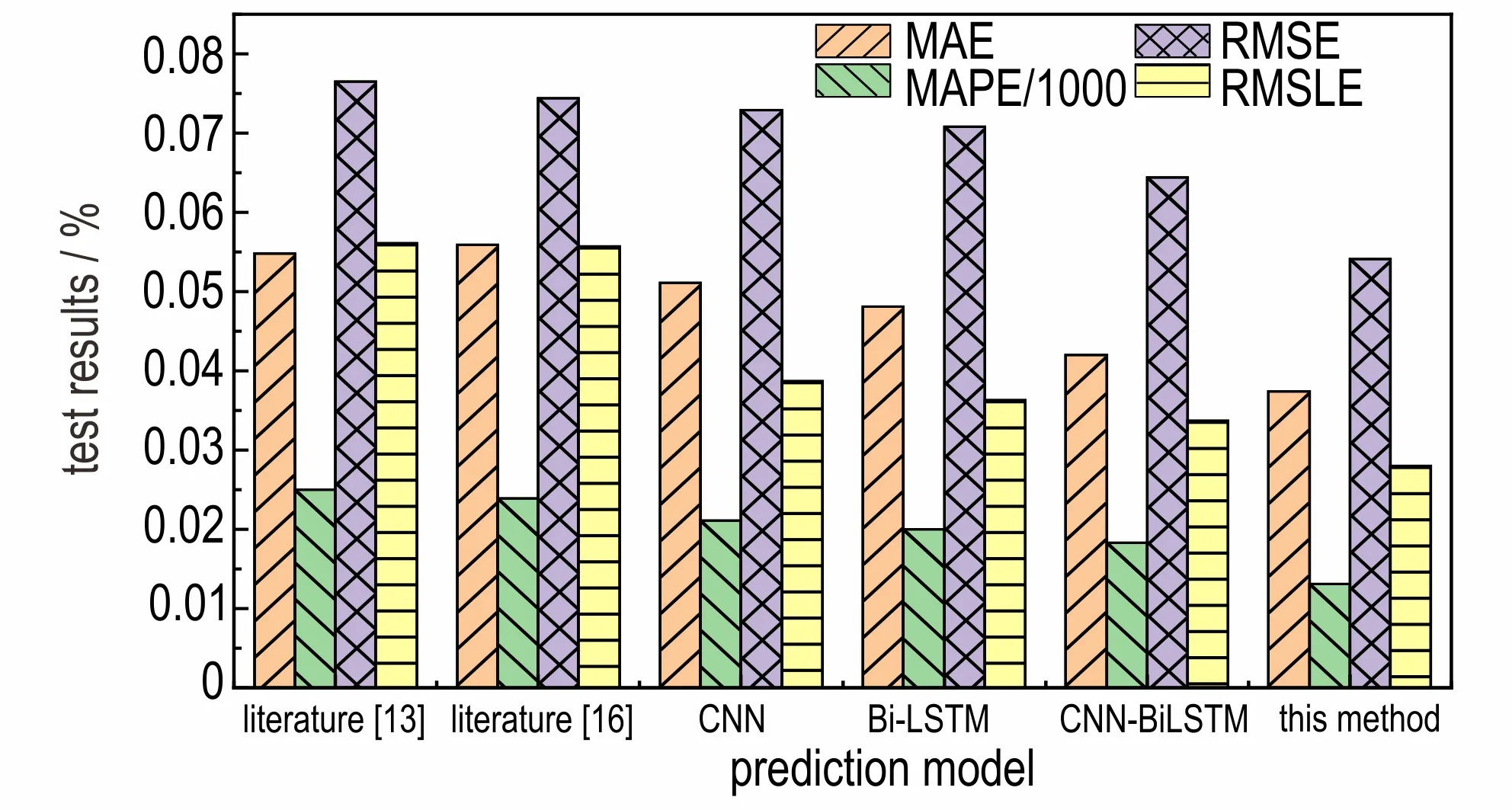
图8 不同模型的生成焓预测效果对比图Fig.8 Enthalpy of formation prediction effect comparison diagram of different model
5 结论
(1)鉴于传统生成焓获取方法(如:实验测试法和高精度计算方法)存在的时间、资源大量损耗和安全方面的问题,提出一种基于深度学习的含能材料生成焓预测方法,实现了“结构-性能”的预测目标;
(2)将代表分子结构的坐标数据转换成库仑矩阵,可有效避免结构数据受到平移、旋转、交换索引顺序等操作的影响;
(3)根据提出的基于Attention 机制的CNN 和Bi-LSTM 融合模型对含能材料的生成焓进行预测时,既可以有效提取数据的特征,又能充分考虑数据间的相关性,同时还能够突出重要特征对预测结果的影响。
(4)对比实验结果表明,本文方法在各个评价指标上均取得了最低的预测误差,表明生成焓的预测效果最好。后期将对数据集进行进一步的扩充,同时进一步优化模型,提高含能材料生成焓的预测效果。
