铁路集装箱轻重货物混合平衡装载研究
2021-02-03雷定猷闫红莹洪舒华张英贵
雷定猷,闫红莹,洪舒华,张英贵
(1. 中南大学 交通运输工程学院,湖南 长沙 410075; 2. 中南大学 智慧交通湖南省重点实验室,湖南 长沙 410075)
高集装箱利用率是集装箱运输企业的不懈追求,但前提是必须符合集装箱装运的安全规定,其中非常重要的就是实现集装箱平衡装载。满足负载平衡约束是达到平衡装载要求的必要条件,即集装箱内所有货物的总重心落在特定的范围之内,货物重量在箱子内的分布均匀[1]。在陆路运输实际中,负载平衡是基本的要求,在确保货物装卸和运输安全、降本增效方面有非常重要的实际意义。如果装入集装箱的货物之间重量差别不明显,不用特意限制一般也能实现负载平衡。然而随着运输种类不断扩展,运输范围不断增大,在装载过程中常常将质量、密度大不相同的不同货物混合装载,如果不进行一定的操作限制,则难以满足负载平衡约束[2]。本文定义质量、密度存在较大差距的货物为轻重货物,将其在满足负载平衡的前提下的装箱问题称为集装箱轻重货物混合平衡装载问题。
近年来,在集装箱布局空间表示方面,Moura等[3]证实了在求解质量和求解效率上,最大覆盖法相比较分割法表现更优;姜义东等[4]提出三维矩形物体布局状态空间分解可以用三叉树来表示。在对装箱货物的处理方式上,Fanslau等[5]提出货物以组合成单元的方式进行装箱,结果显示单元装载相较单个装载有更高的效率;朱向等[6]将装载优化建立在将特定类型的货物组合成特殊形状单元的基础上;Araya等[7]构建了评估货物单元的函数;雷定猷等[8]提出了利用重货单元构建中心骨架来控制重心位置的思想。在负载平衡约束方面,Costa等[9]、Trivella等[10]都将约束转换成了纵、横和竖直三个方位的限制条件;Alonson等[11]通过限制总重心位置满足负载平衡要求;Moon等[1]将约束转换成限定范围;Ramos等[2]在统计测算负载后,将其表示为直观分布图;杨广全等[12]基于集装箱装运车辆具体的技术参数,分析提出了装车后车辆转向架各类指标的计算公式。之前对于轻重货物混合平衡装载问题的研究不多,而且大多将约束简单转化或是作为装载方案的评价指标,没与实际装运情况糅合分析[2],难以确保集装箱高利用率的同时达到平衡装载需求。
本文结合负载平衡约束,基于铁路集装箱装运车辆实际,针对轻重货物,构建了集装箱平衡装载模型,研究分析布局空间和待装箱的轻重货物,将待装箱货物细分并组合成货物单元,再利用启发式算法对货物单元进行装箱,以此为基础设计求解算法。最后,对算法进行测试,并与采用其他算法所得结果进行对比分析,验证有效性。
1 模型建立
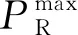
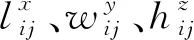
(1)
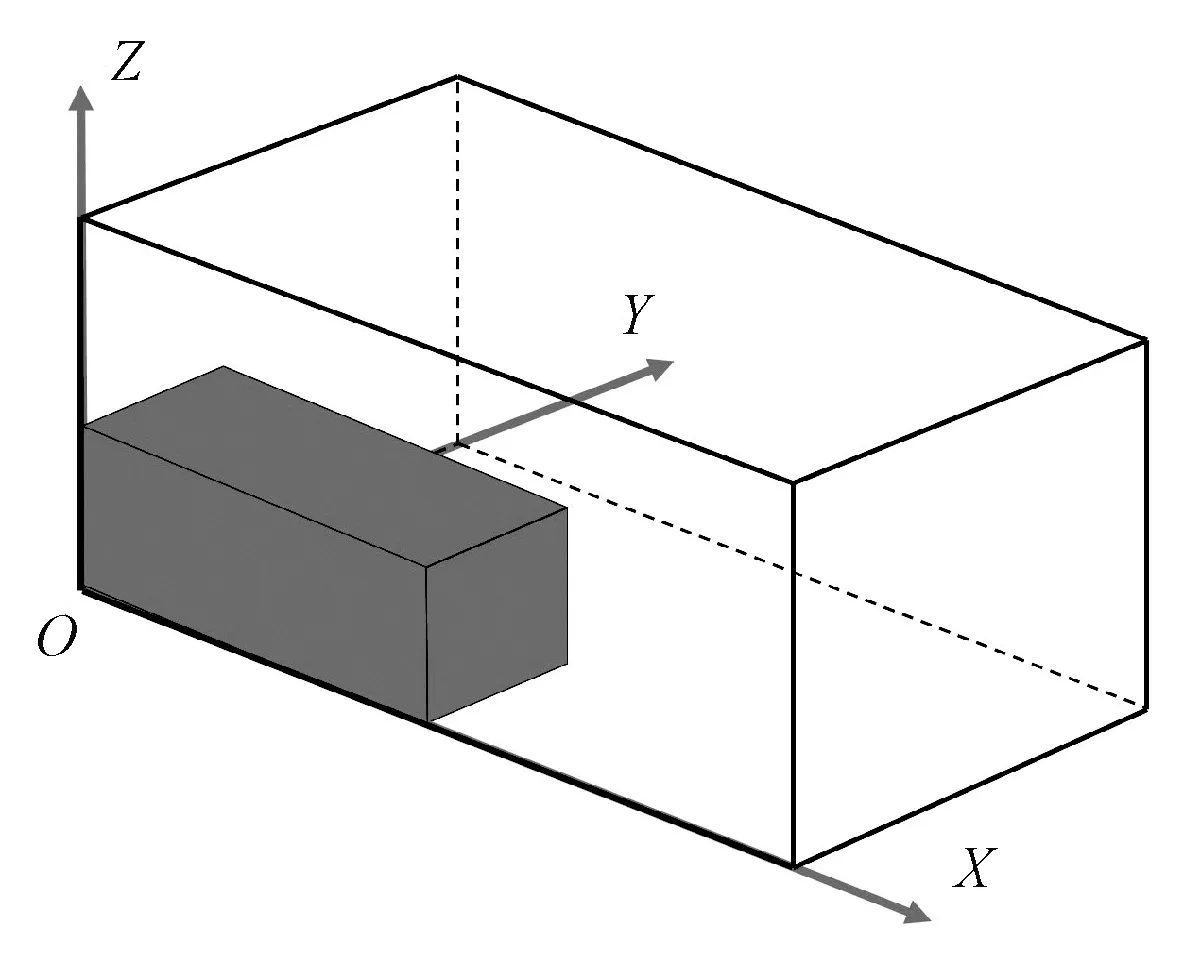
图1 集装箱三维坐标系示意
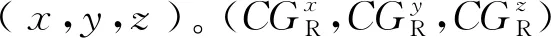
(2)
(3)
(4)

图2 一个集装箱装车位置示意
由此可得箱货总重心偏离车辆横纵中心线距离d1和d2,以及重车重心高d3为
(5)
(6)
(7)
至此有负载平衡表达式为
(8)
装运两个及以上集装箱时,无论是单层还是双层装运,其计算过程与上述过程类似,主要区别在于求箱货总重心位置时,需分别在每一个集装箱各自坐标系中单独计算,确定集装箱具体装车位置以后,再转化至同一坐标系求所有集装箱及货物的总重心位置。亦可优先确定各集装箱的装车位置,建立统一的坐标系进行货物装载和计算。此处以单层装运两个相同集装箱为例,集装箱放置于车上的位置见图3。
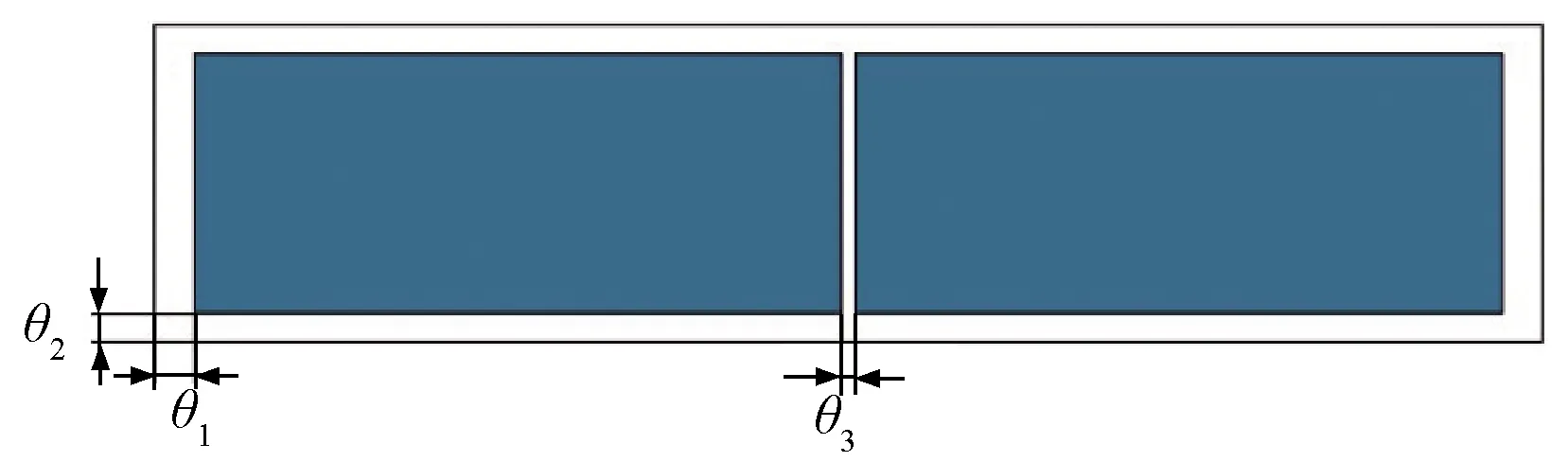
图3 两个相同集装箱装车位置示意
同样地,于图3中以铁路车地板的左下角在轨面上的投影为坐标原点建立三维坐标系。P1和P2分别为两集装箱内货物总重量。货物总重心在各自集装箱内坐标系中的坐标分别为(x1,y1,z1)和(x2,y2,z2),其在新坐标系中可分别表示为
(9)
(10)
由此可得新坐标系下两集装箱和所有货物的总重心坐标为
(11)
(12)
(13)
把式(11)~式(13)代入式(5)~式(7)即可得到对应的表达式。
综合以上分析,构建模型
(14)
s.t.
式(8)
(15)
(16)
(17)
(18)
2 算法设计
分别对布局空间和装箱货物两个主体进行分析,设计求解算法。
2.1 空间划分、选择与更新过程
采用最大覆盖法划分空间,即用如图4中r1、r2、r3所示的3个长方体来表示剩余空间,此方法可以使布局空间选择接收更多不同组合的货物单元。
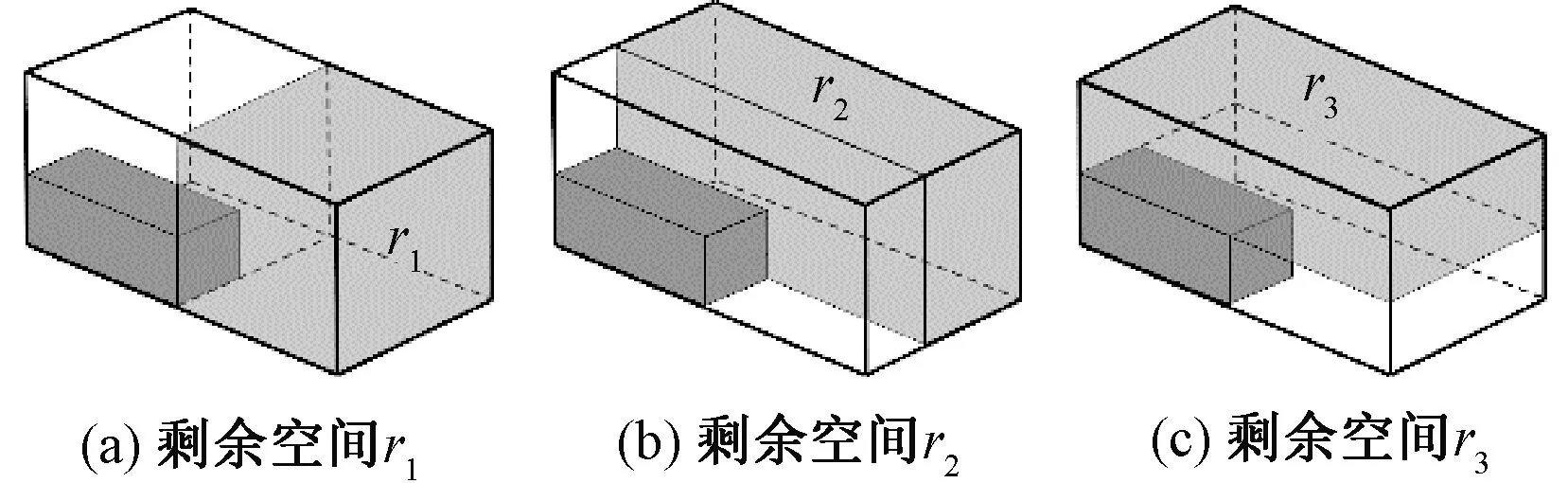
图4 最大覆盖法示意
下面开始选择每一阶段的空间,如图5所示,假设某一空间r的顶点ve1的坐标为(x1,y1,z1),ve1对应的集装箱顶点VE1的坐标为(x2,y2,z2),则两点之间的曼哈顿距离为|x1-x2|+|y1-y2|+|z1-z2|。集装箱和空间r之间共有8对相对应的顶点,即存在8段曼哈顿距离,定义最小者为空间r的锚距,定义锚距相对应的空间r的顶点为锚角。将货物放在拥有最短锚距的空间的锚角处,若多个空间同时拥有最短锚距,则选取体积较大者。此方法可使货物沿着集装箱内壁布局,慢慢将剩余空间汇集在箱体的中间部分,便于剩余空间的再次利用。
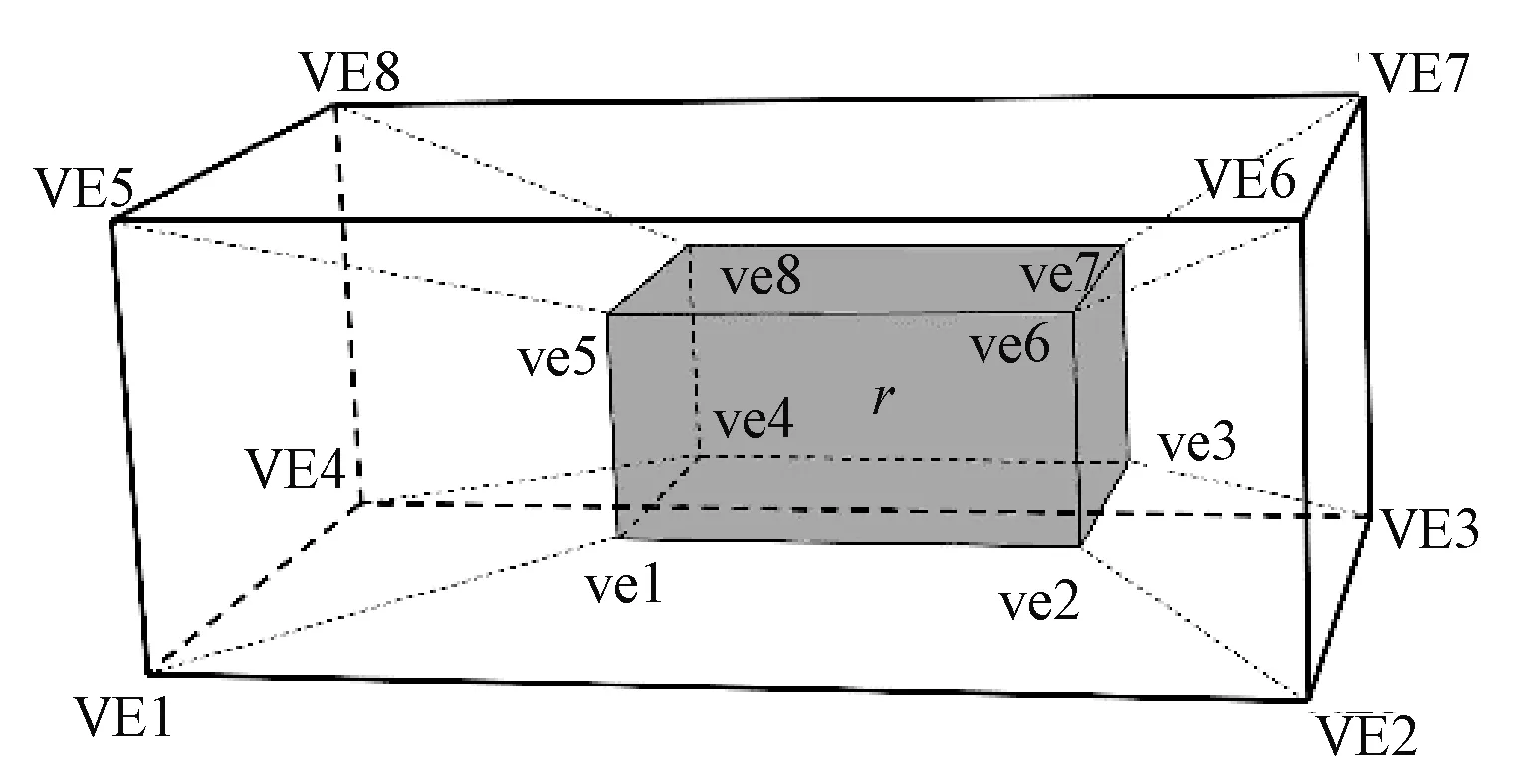
图5 集装箱与空间位置关系示意
在货物放进被选择的空间之后,采用最大覆盖法划分出3个新的剩余空间。如果存在其他的空间与放进空间的货物相互重叠的情况,则需要重新表示这些空间。除外,需要核查现有空间是否已经是最大空间,删去尺寸为零、重复表示或者已经包含在最大空间里的空间。
2.2 轻重货物单元装载规则
先按照重量和密度对轻重货物进行分类,接着分别构造重货和轻货单元,最后使用不同的启发式方法先后处理重货单元和轻货单元。
(1)货物分类
货物对总重心位置的影响与其重量和密度成正比,按照货物的重量和密度进行两次排序分类,以待装货物重量的λ倍作为重货重量,确定重货集合。λ为重货占比系数,其值与待装货物标准差成正比,通过算例测试,可知货物重量标准差与重货占比系数的对应关系如表1所示时,重货能够较有效地构建中心骨架。

表1 重货占比系数取值
算法 1
输入:待装箱货物集合C,重货占比系数λ。
输出:重货集合K。
Step1确定候选货物总重量和体积。QK和VK分别候选货物的总重量和体积。若VT≤V,令VK←VT,QK←QT;否则找到a0使得V1+V2+…+Va0≤V且V1+V2+…+Va0+Va0+1>V,令VK←V1+V2+…+Va0,QK←Q1+Q2+…+Qa0。再与集装箱载重量比较,QK←min{Q,QK}。
Step2排列候选货物。将候选货物按照类重量由大到小的顺序排列,在类重量相等的情况下,将货物数量相对少的类排列在前;取前a1=0.5n+1类,继而按照类密度由大到小顺序排列,在密度相等的情况下,货物数量少的排列在前。设该排列为C1,C2,…,Ca1。
Step3确定重货。对于上述排列,找到a2使得Q1+Q2+…+Qa2≤λQK且Q1+Q2+…+Qa2+Qa2+1>λQK。
Step4返回K={C1,C2,…,Ca2}。
(2)货物单元构造
构造货物单元可实现货物的高效装载。货物单元会继承构成它的货物的属性,例如货物单元的尺寸和重量通过累加单个货物的尺寸和重量得到,放置方位为货物单元包含的所有货物放置方式的交集,位置坐标由货物单元放入集装箱后其左内下角坐标确定,重心坐标由货物总重心计算公式(式(1))得到。应该特别注意的是,同一个货物可以组合在不同的单元中,所以为了保证剩余的单元是由未装箱的货物组合而成,当货物单元b被放入箱中后,包含b中一个或多个货物的其他货物单元都要删掉。
算法 2
输入:重货集合K,生成重货单元数NK(常取10 000[5]),有效体积占比v(常取98%[5])。
输出:重货单元集合B。
Step1初始设置。由于单个货物亦可视为一个单元,因此将B←K;将B′←B以遍历组合;将SA←φ用于保存符合构造要求的单元。
Step2进入遍历组合。对于B′中所有单元bi∈B′,与B中所有单元bj∈B逐一进行组合。将bj分别放置在bi的X、Y、Z方向,构成重货单元bk。如果bk中包含的货物总体积和bk最小外接长方体体积的比值大于v,将SA←SA∪{bk}。
Step3生成单元数判断。Step2结束后,如果SA≠φ,将B←SA∪B,将B′←SA,SA≠φ。同时进行判断,如果B中元素个数|B|>NK或者集合SA=φ,转Step4,否则转Step2。
Step4得到重货单元集合B。
(3)重货单元处理
重货在很大程度上决定了总重心位置,因此采用中心骨架策略[9],通过重货单元来大概确定总重心位置;而后通过算例测试,提出新的重货单元筛选规则,从而有效提高重货单元组合的成功率。
算法 3
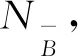
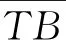
Step1搜索能够用于构建中心骨架的重货单元或者单元组合。设重货单元总重量为QB,从B中取出一个重货单元,重量为qb,如果符合式(19)那么可单独构建1中心骨架;如果符合式(20)或式(21),那么继续搜索符合相同条件的,且不包含同个货物的重货单元,构建2、3或4中心骨架。搜索到满足条件的重货单元,则将能够构建中心骨架的单个重货单元或者多个单元组成的组合作为cp,并更新SK←SK∪cp;否则转Step3。
qb≥0.8QB
(19)
0.4QB≤qb≤0.5QB
(20)
0.2QB≤qb≤0.3QB
(21)
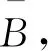
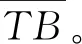
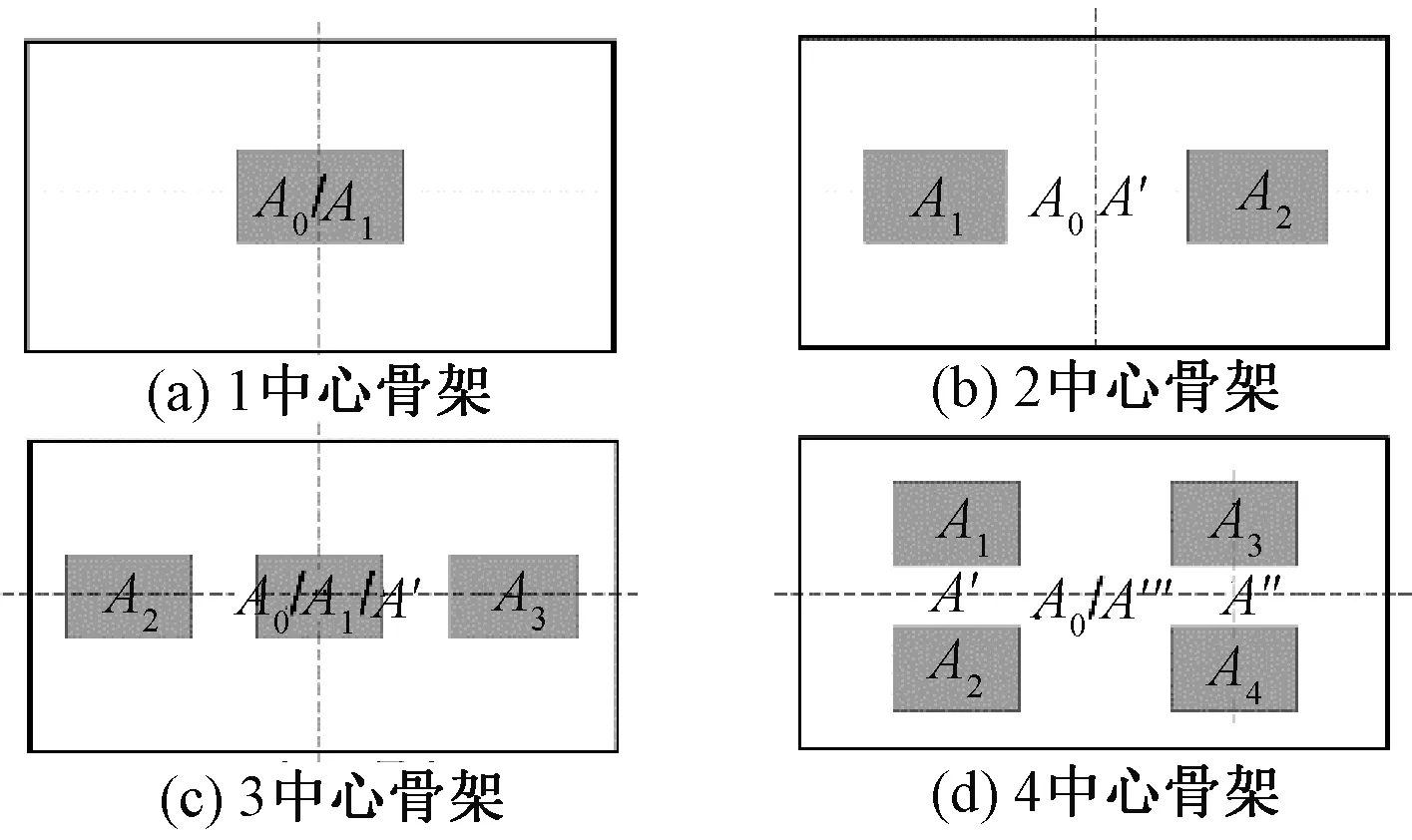
图6 中心骨架构建示意
理论上中心骨架数量可增加,但中心骨架对布局空间造成的分割及自身的不稳定性与其数量成正比,由此只考虑4及以下的中心骨架。得到候选集合SK后,取出重货单元组合装入箱中,如果装箱方法有多种,那么选取能够使得集装箱重心最低的方法进行装箱。图6中,外部的框线表示的是箱子底面轮廓,灰色的方块表示的是重心投影在A1、A2、A3、A4的重货单元,A″为A3和A4重心投影,A‴为总重心投影。构建中心骨架时,重货单元组合的重心投影A′要与集装箱底面几何中心A0重合,或两者偏差在规定范围内。
若所得方案不满足负载平衡约束,则对构成中心骨架的重货单元位置进行调整,使得货物总重心在底面上的投影落在箱子底面几何中心附近满足偏移规定的区域。图7分别给出了图6(b)、图6(c)和图6(d)所构建的3种中心骨架各两种可操作的移动方法。
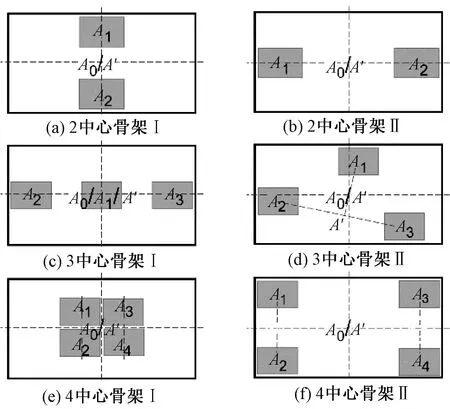
图7 中心骨架移动示意
(4)轻货单元处理
构建好中心骨架后,使用下面启发式轻货单元评估函数,从对应轻货单元集合中择优选择轻货单元完成剩余装载布局。
(22)
式中:Vol(b)为轻货单元b的体积;Wei(b)为b的重量;Cov(b,pl)为单元b装箱后,由箱体内壁及相邻近的单元覆盖的表面积与单元b总表面积的比值。如果邻近单元bi的面F在单元b的正交投影覆盖了b表面,并且F和单元b表面之间的正交距离等于或小于pl与pl所在坐标轴方向上b的尺寸乘积,则块b的表面积被块bi覆盖;Cov(b,pl)越高,说明b和空间匹配度越高;b放入r后的空间损失率用Loss(b,r)表示,基于还没有装箱的轻货单元,求解剩余不能利用的体积问题可转化为对b的X、Y、Z方向的一维背包问题,求得的值与空间r体积的比值即为Loss(b,r);体积小的货物可以用来填充剩余的小空间,因此,将体积小的货物放在最后似乎是合理的,然而大的单元可能是由众多小的货物构成的,Num(b)为单元包含的货物数量,Num(b)值越大,代表组成货物体积越小,反之亦然。最后,生成了如式(22)所示包含由非负参数α、β、γ、δ和ε加权的所有准则的评估函数。
算法 4
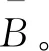
输出:轻货单元b0。
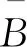
Step2同理继续向下求解。分别选出ω个解(Step1得到)后一步的r′,r′∈R,然后取出评估值前ω的单元,逐个放置于布局空间r′锚角处,由此产生ω2个解,更新集合。
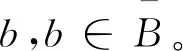
Step4得到最优解。最终得到ω2个解,判断得到最优解best,以及其对应的轻货单元b0,b0则为当前应装箱的单元。
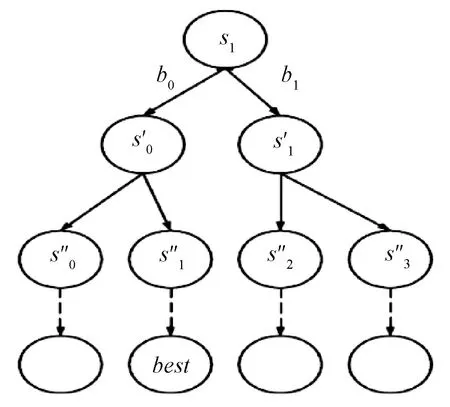
图8 轻货单元选择示意(ω=2)
2.3 轻重货物混合平衡装载算法
综合以上,设计求解轻重货物混合平衡装载的启发式算法。
算法 5
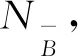
输出:装载方案sbest。
Step1货物分类。根据算法1得到重货集合K。
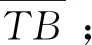
Step3构建中心骨架。进行判断SK=Φ,如果是,转step7;否则取一个cp,同时R′←R,C′←C,用cp在R′中构建货物单元的中心骨架。
Step6循环判定。判断所有组合是否已遍历完,如果是,转Step7,否则转Step3。
Step8返回sbest。
3 算例分析
通过对国际标准算例及轻重货物算例进行仿真测试,验证本文算法的有效性。
3.1 标准算例
表2中,使用本文算法得到的集装箱容积利用率(Vol.)略低于其他算法,比最优者低1.55%。其原因主要是本文设计的算法以树形检索为解空间搜索内核,以确保每次选到的货物单元都是最适合的,搜索能力弱于以遗传算法为内核的算法。算例使用本文算法得到的负载失衡的算例数(Unb.)均为0,百分百满足集装箱装载平衡条件,但是其他最好的结果也可以达到98.20%,这方面差别微乎其微。通过计算直观清晰看到,基于f(x,2,5)求得的结果,货物的负载均匀,密度期望基本可以看作为ρc,方差非常小,只要简单处理就能够满足平衡。根据结果可知,本文设计的算法一定程度上具有普遍适应性,但是仍然不足以说明其对混合平衡装载是有效的,对此还需要进一步的测试。
3.2 轻重货物算例
基于标准算例,增大货物密度区间,减小密度下限值,密度上限保持当前载重允许最大值。令ρmin=0.05ρc,ρmax=Q/[m0(n-i0)],其中n为货物种类数目,i0为已经给出了重量的货物的种类数目,m0为已经给出了重量的货物的数目。与此同时将贝塔分布改为f(x,0.075 ,0.075 ),基于修改后的参数重新进行测算,两贝塔的分布概率密度差异见图9。基于此重新生成1 500个算例,保持其他条件不变,结果见表3。
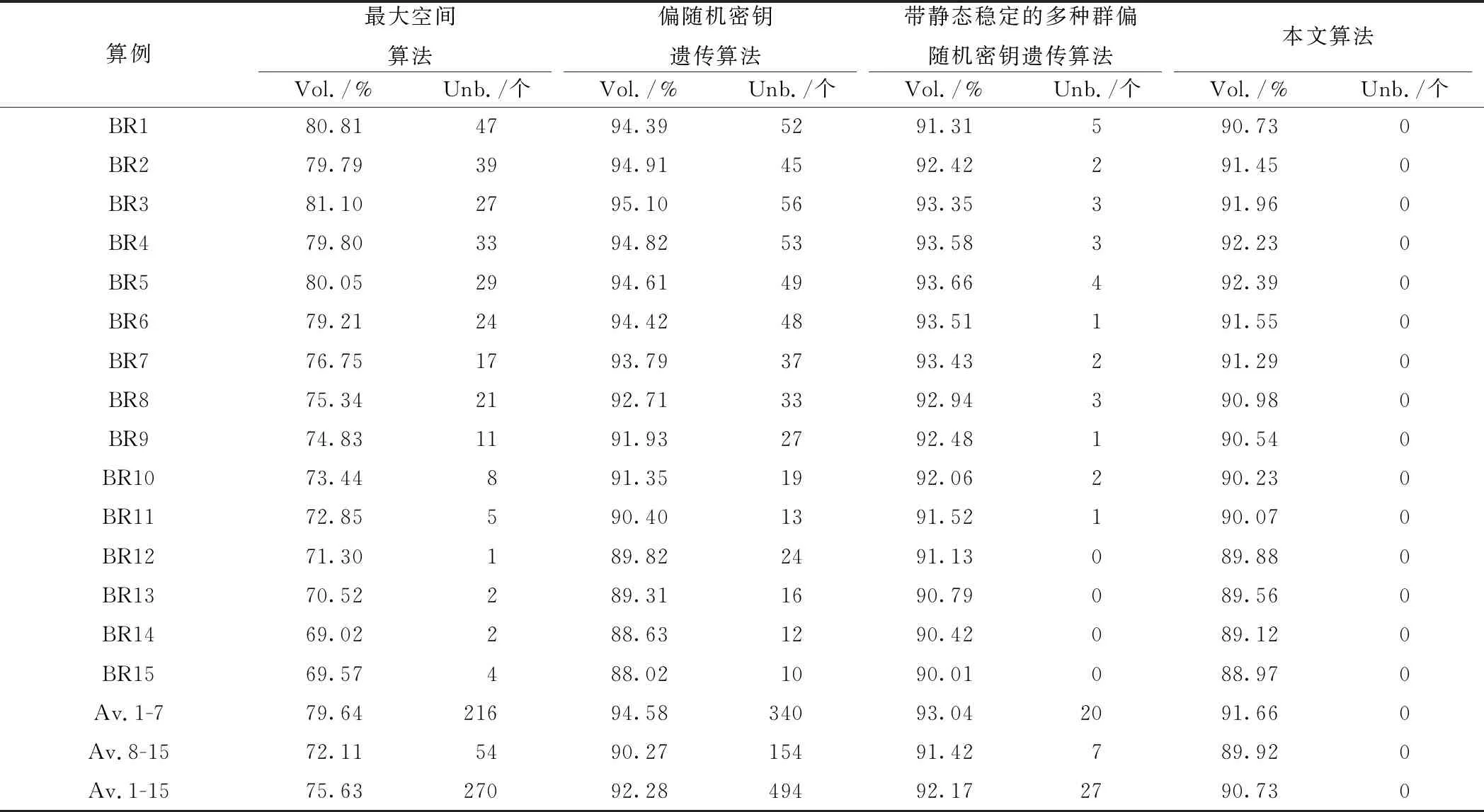
表2 标准算例测试结果
从上述测算数据可得,装载货物属性一旦改变,对结果会造成非常大的改变。所有算法测算结果在集装箱容积利用率方面都有所下降,但是总体来说保持稳定状态;但是在负载平衡方面表现非常明显,本文所优化算法负载平衡条件平均满足率相较最高,达95.20%。
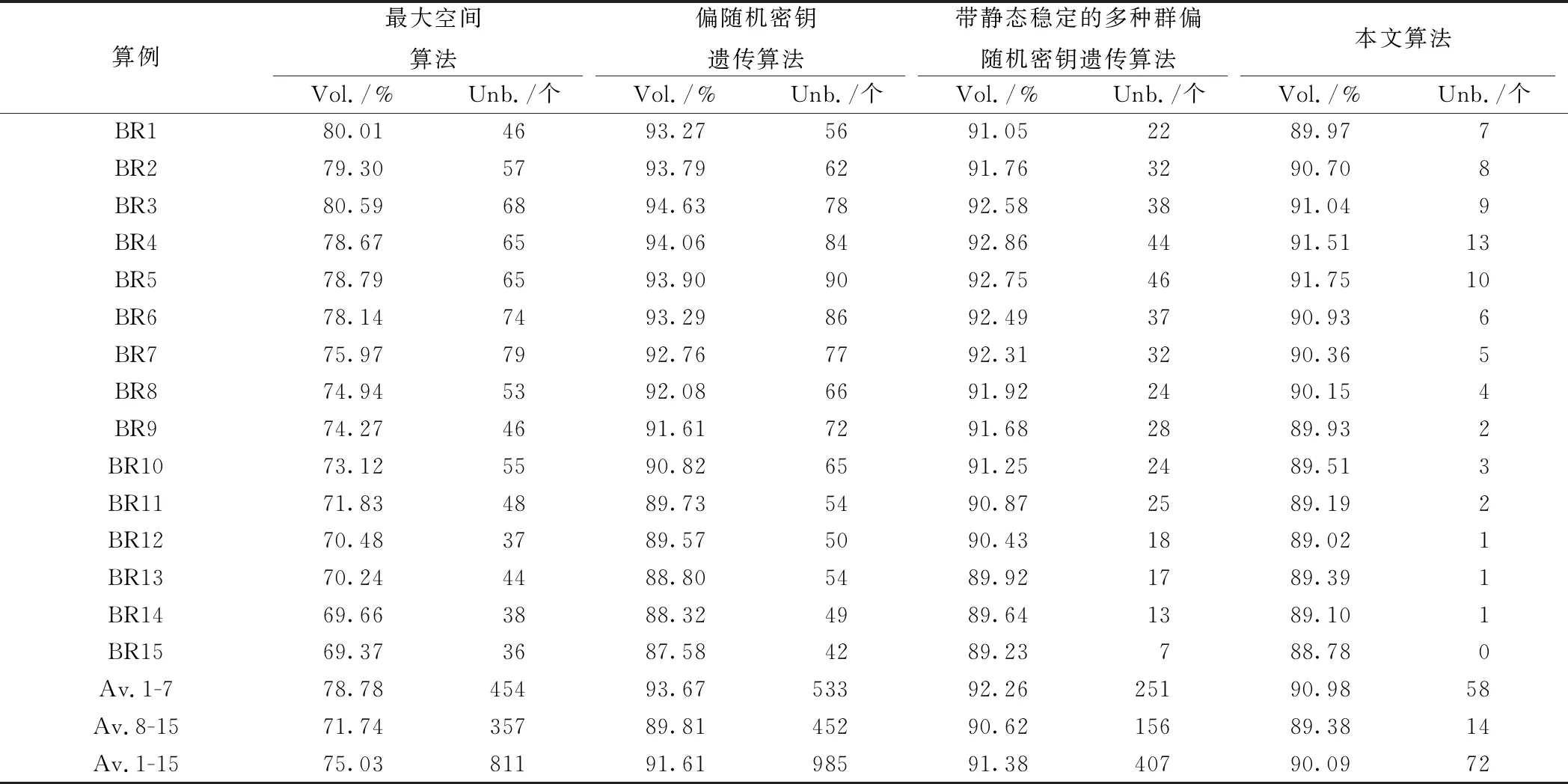
表3 轻重货物算例测试结果
4 结论
(1)结合负载平衡约束,基于铁路集装箱装运车辆,建立轻重货物混合平衡装载模型;将等待装箱的货物细分为轻重货物单元,使用评估函数对轻货单元进行选择装载,形成完整的货物装载方案,设计相应求解算法。
(2)构建的模型和求解算法有效地实现了轻重货物混合平衡装载,可以确保集装箱容积平均利用率不低于90%,同时有95.20%以上的概率满足负载平衡约束。
(3)未来可根据待装货物密度和体积情况,同时考虑优化集装箱的重量利用率。
