桥上CRTSⅡ型板式无砟轨道温度作用取值研究

梁金宝，戴公连，唐 宇，杨凌皓

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 中铁第四勘察设计院集团有限公司，湖北 武汉 430063)

无砟轨道由于其稳定性高、平顺性好、维修工作量少等众多优点已被广泛应用于我国高速铁路建设[1]，其中CRTSⅡ型板式无砟轨道技术在我国京津、京沪、宁杭及沪昆等客运专线得到广泛应用[2]。由于混凝土结构的导热系数较小[3-5]，自然环境下的轨道结构受太阳辐射和对流换热等热边界耦合影响，结构内外温度表现不均衡，其中竖向温度梯度作用是导致结构上拱变形和层间黏结性能疲劳减弱的主要原因[6-7]；其次，在季节性的气候周期下，轨道结构均匀温度随大气均匀温度变化而变化，导致结构季节周期性的伸缩变形[8]。

针对无砟轨道温度作用取值，国内学者通过试验测试、理论计算的方法开展了广泛而深入的研究，试验研究主要集中在对典型天气或季节结构温度测试数据的处理分析[9-10]，测试数据时间较短，缺乏结构温度长期监测样本，难以精确描述轨道结构最大温度作用的实际特征；理论计算主要集中在对轨道结构温度场气象参数的分析[11-12]，建立热传导方程，施加气象参数边界条件进行计算，由于自然环境下的轨道结构热边界复杂，影响因素较多，计算结果存在一定的局限性。已有的研究对象中对曲线段CRTSⅡ型板式无砟轨道温度时程规律的研究甚少，对轨道结构年均匀温度作用讨论较少；同时对于轨道结构温度梯度而言，偏离主体的最大梯度样本部分为工程设计所关注，单一极值分布并不能对梯度样本“高尾”情况进行很好地拟合。

本文以桥上曲线段CRTSⅡ型板式无砟轨道结构为研究对象，通过三年的数据采集，采用时间序列差分法将温度时程曲线趋势变化和短周期变化进行分解，得到受大气环境影响的结构均匀温度时程，并用傅里叶级数拟合，通过建立GPD(Generalized Pareto Distribution)模型对尾部数据进行拟合，提出适用于桥上曲线段CRTSⅡ型板式无砟轨道的竖向温度梯度拟合模式。

1 工程背景与测点布置

以沪昆高速铁路某简支梁桥上曲线段CRTSⅡ型板式无砟轨道为工程背景，该桥位于东经115°、北纬28°，桥梁轴线方位角为87.5°，轨道结构超高38 cm。通过预埋温度计的方法单侧布置测点，将温度元件全部接入数据采集仪中实现自动采集存储，测试截面位于箱梁固定支座轨道板接缝处，见图1。

轨道结构温度作用研究选取具有一定代表性的监测数据(2013-10-03T00:00：00—2016-10-03T00:00：00时)进行分析，各测点采样周期为30 min，除仪器故障等原因导致数据缺失，三年共采集41 268组数据，以截面Ⅱ测点L为例，其温度时程曲线见图2。

2 GPD模型估计理论

2.1 GPD模型参数计算

极值理论指出，对于广义极值分布，当有足够大的临界点u，即x>u时，超越u的X样本服从GPD模型，即

(1)

式中：ξ为形状参数；σ为尺度参数；u为设定阈值。在阈值u确定的情况下，随机变量Ti*的累计概率函数可表示为

(2)

阈值u越大，则尾部样本数据越少，数据方差越大；反之阈值u越大，尾部概率分布与GPD模型不吻合，尾部样本量成为有偏估计。目前通常采用平均剩余寿命图法来确定阈值，该方法较大程度上存在一定的主观性，本文在平均剩余寿命图法的基础上，采用MSE(Minimum Squared Error)方法来确定尾部样本量，即

(3)

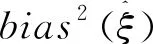
随机过程中对参数估计的方法主要有极大似然法、矩估计法等，也有部分参数估计法基于这两种方法进行改进。通过对以上两种方法进行适用性比较，可以发现，矩估计法在形状参数ξ趋近于0时，对具有少量的尾部样本估计准确率最佳[13-14]，本文主要采用矩估计法对参数ξ进行估计，即

(4)

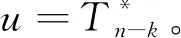
利用经验累积概率分布函数，在阈值u确定之后构造散点，其表达式为

(5)

(6)

式中：j=n-k+1,…,n。利用程序对尾部散点样本数据进行统计，采用线性回归法对尺度参数σ进行估计。

2.2 GPD模型温度梯度极值计算

(1)根据曲线段轨道结构对应截面实测温度数据，分别取差值得到梯度数据样本，将对应t时间段内的梯度样本以间隔时期ΔT(1 d)进行划分，统计对应时间段样本的最大值Ti，得到梯度最值样本{Ti}(i=1,2,…,n)，将最值样本{Ti}进行排序得出顺序统计量{Ti*}，其中T1*≤T2*≤…≤Tn*。

(2)构造经验累积概率分布函数为

f(Ti*)=i/(n+1) 1≤i≤n

(7)

(3)确定模型参数取值。

(4)建立GPD数学模型对尾部样本数据进行拟合，考虑到温度梯度数据样本以间隔ΔT(1 d)来划分温差最值，故取对应重现期Tre年的概率分位值为1/(365×Tre)，结合ξ值的正负情况，对应不同概率需求的温差值Tc可表示为

(8)

(9)

并对ΔT的分布函数进行对应100 a重现期的温度梯度极值计算。

3 轨道结构温度作用取值分析

3.1 温度时间序列分解

对于轨道结构的温度监测而言，其温度时程曲线主要包括整体趋势变化与局部短周期变化的两种时程成分。趋势变化主要为结构测点温度随四季气温变化的趋势，代表温度时程曲线的整体走向；短周期变化表示为结构测点温度在以日照为主的作用下，以日为周期发生的升、降温过程。

采用时间序列差分法将时程曲线的整体趋势变化和局部短周期变化进行分解[15]，以日为单位，对原始数据进行时间序列分解，得出其趋势变化的时程曲线。考虑到数据差分使用了平均处理的方法，因此可将测点温度整体趋势变化的时程曲线定义为均匀温度曲线。测点L的均匀温度时程见图3。

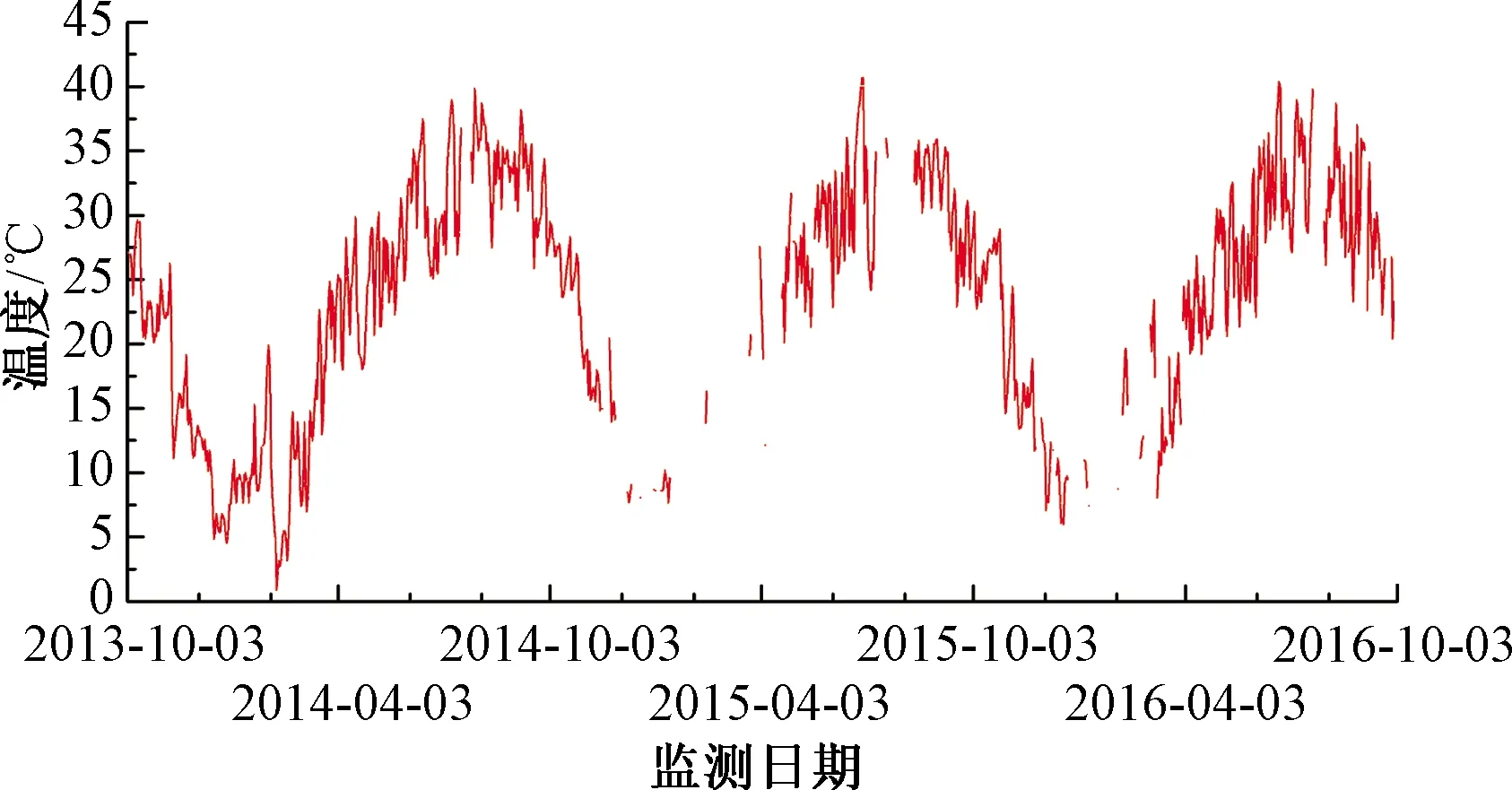
图3 测点L均匀温度时程曲线图

由图3可知，测点L均匀温度时程反映了该测点位置的均匀温度随四季气候变化的基本规律，测点均温夏季高，冬季低，整体趋势呈三角函数规律变化，年周期性表现明显。

将测点L的原始温度样本减去其对应的均匀温度，可得到具有以天为周期变化的波动温度，波动曲线变化可理解为受到日照等因素引起的日温度升、降温过程，见图4。

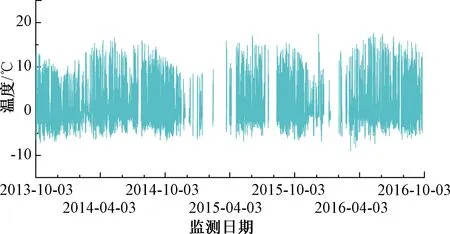
图4 测点L波动温度时程曲线图

由图4可知，波动温度在0 ℃线附近以日为周期上下波动，符合太阳辐射变化周期的自然规律。

3.2 均匀温度分析

结构均匀温度变化一般影响着结构的轴向变形，其轴向伸缩量可能控制着结构整体设计。为研究轨道结构整体均匀温度时程变化规律，采用上述方法计算轨道结构各测点的均匀温度，结果显示各测点的均匀温度变化规律基本一致，可用一条统一的时程曲线来描述轨道结构整体均匀温度特征，故将各测点均匀温度时程取平均得到轨道结构整体的均匀温度时程。

考虑到轨道结构整体均匀温度时程曲线是一种周期性变化过程，故可用傅里叶级数对该曲线进行拟合，并对周期进行物理意义修正，拟合方程为

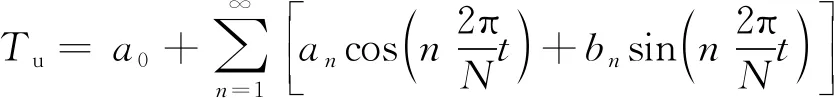
(10)

式中：Tu为结构均匀温度；t表示时间日序号，以1月1日为第一天；N表示一年总天数，取365；a0、an、bn为拟合参数，其中a0代表测点年均匀温度。

在实际拟合中，一阶拟合优度已达0.9以上，满足拟合精度要求，式(10)可表示为

(11)

采用三角函数变换对式(11)进行简化，即

(12)

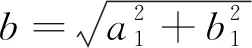
根据式(11)对轨道结构整体均匀温度时程进行拟合得到参数a0、a1、b1分别为21.38、3.659、-10.69，相关系数平方为0.930 4，利用三角函数变换得到轨道结构整体均匀温度时程表达式为

(13)

由式(13)可知，轨道结构年均匀温度为21.38 ℃，年均温的变化幅值为11.3 ℃。

由于实测结构整体均匀温度时程曲线存在上下波动的“毛刺”现象，因此将均匀温度实测值与傅里叶拟合值做差作为结构均温波动统计样本，得到轨道结构均温波动正负温差最大值分别为8.27、-8.69 ℃，根据均温波动实测最值对式(13)傅里叶拟合曲线上下平移，得到轨道结构均匀温度最值包络线，见图5。

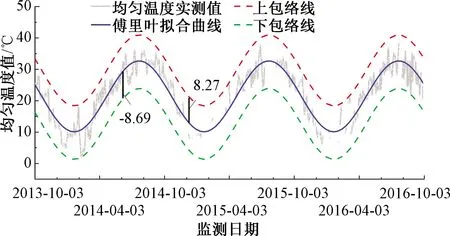
图5 轨道结构均匀温度曲线图

3.3 温度梯度分析

考虑到轨道结构受温度梯度变化，将产生一定的竖向挠曲变形，从而影响轨道结构的平顺性。为研究轨道结构竖向温度梯度变化规律，选取位于结构中部相关位置测点，且对轨道结构有良好代表性的截面Ⅱ进行梯度模式分析，同时刻结构竖向温度梯度可用方程表示为

ΔT=(Ti-Tu)-(Tj-Tu)=Ti-Tj

(14)

式中：ΔT为不同位置温度梯度；Ti与Tj为不同测点原始温度；Ti-Tu为i测点波动温度，j点亦同。

为确定轨道结构竖向温度基准点，采用时间序列分解法计算截面Ⅱ各测点的波动温度，见图6，由图6可知，从上到下各测点的波动变化范围逐渐减小并趋于稳定，因此选用波动最小的测点P作为温度基准点进行温差计算。

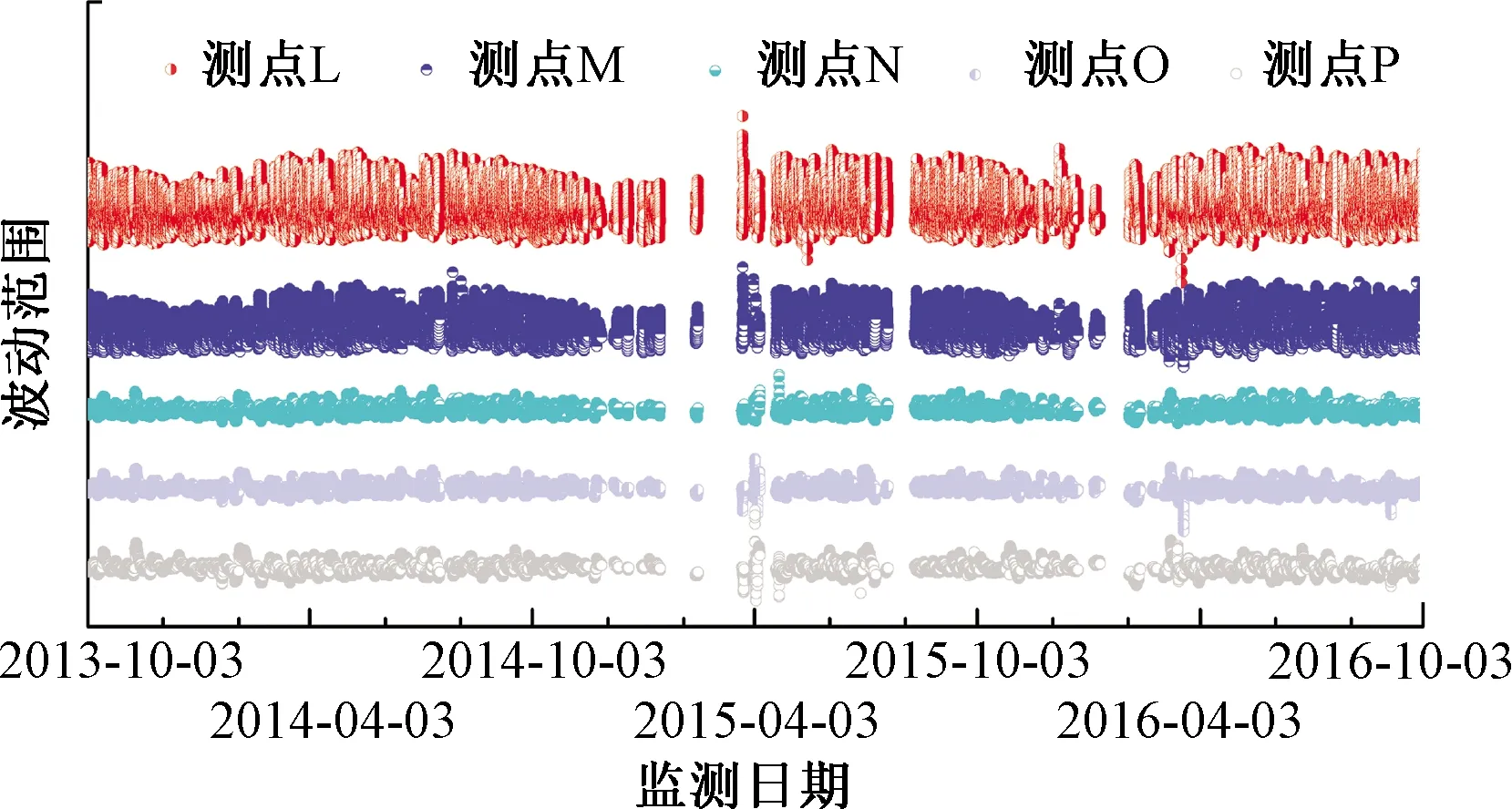
图6 截面Ⅱ波动温度范围图

利用三年共41 268组数据进行轨道结构竖向温度梯度研究，将截面Ⅱ测点L、M、N、O分别与P点温度数据样本做差，得出相应的温差样本，并进行正负温差分类。根据截面Ⅱ测点L与测点P日最大温差样本，利用极值概率理论得到对应温差统计量与累积分布之间的关系，见图7。

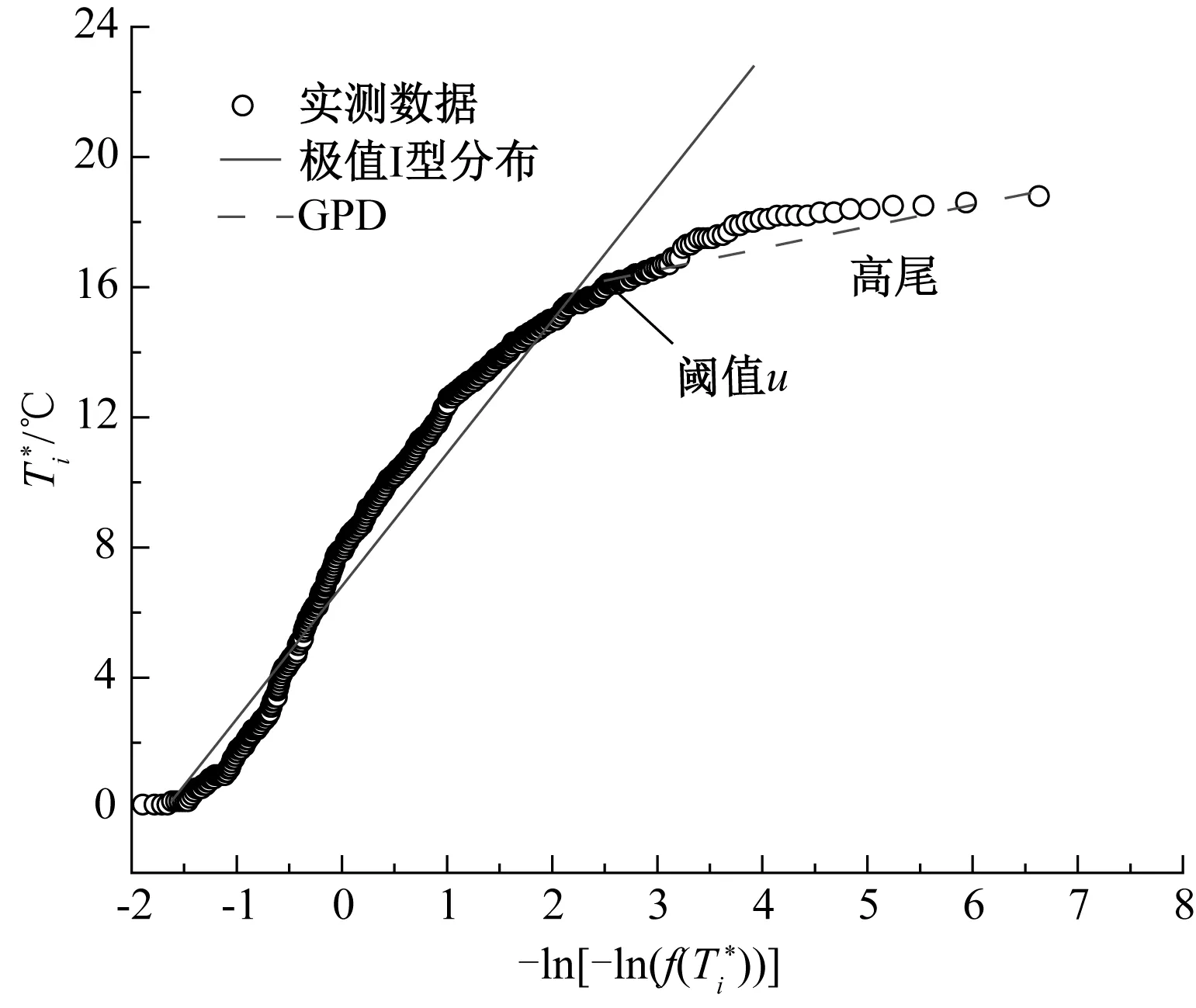
图7 极值理论温差概率分位图

由图7可知，高尾部分的线性趋势明显偏离主体数据样本，极值尾部数据展现出一定的线性趋势，但线性规律却存在不同，对其极值分布模拟时应采用不同的分布参数，尤其是偏离主体的最大温差极值样本为工程设计所关注。根据2.1与2.2节所述，对截面Ⅱ温差统计样本采用GPD模型进行模拟，得到对应不同概率需求的温差表达式参数见表1和表2。

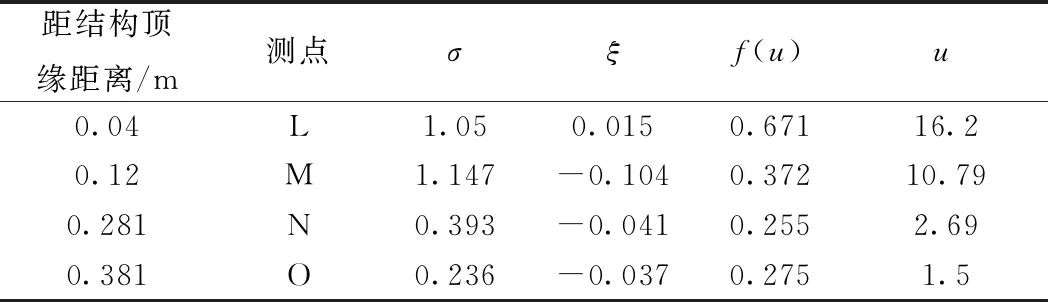
表1 截面Ⅱ正温差表达式参数统计值

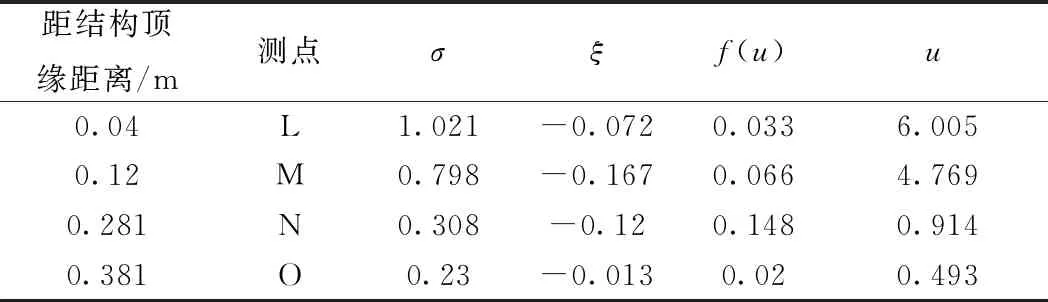
表2 截面Ⅱ负温差表达式参数统计值

根据ξ值的正负情况，将表1和表2所得参数值带入式(8)、式(9)，取Tre=100 a得出其对应100 a重现期的正负温差估计值，结果见表3。

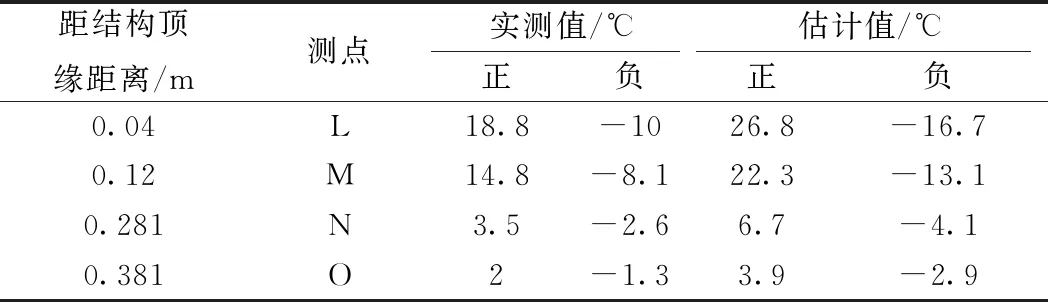
表3 截面Ⅱ竖向各测点温差统计值

由表3可知，测点L与测点P最大正负温差分别为18.8、-10 ℃，采用GPD统计模型对样本进行计算，得出百年一遇的正负温差代表值分别为26.8、-16.7 ℃。对轨道结构竖向实测与估计梯度参照我国铁路规范的指数曲线形式进行拟合，拟合度均在0.98以上，截面Ⅱ正负实测值与百年一遇估计值拟合指数曲线见图8。

图8 截面Ⅱ竖向温度梯度拟合曲线

由图8可知，曲线段轨道结构竖向温度梯度实测最大升温模式为Ty=25.23·e-5.943y，百年一遇升温模式为Ty=36.21·e-5.615y；实测最大降温模式为Ty=-13.13·e-5.367y，百年一遇降温模式为Ty=-21.74·e-5.307y。

4 结论

本文基于曲线段CRTSⅡ型板式无砟轨道三年的温度实测数据，采用温度时间序列分解与GPD极值统计等方法对轨道结构均匀温度与梯度进行分析，得到如下结论：

(1) GPD数学统计模型可以计算对应不同重现期内的温度梯度代表值。通过对各类统计尾部样本数据进行计算处理，预估不同概率需求的温度梯度模式。

(2) 采用时间序列差分法对轨道结构温度数据时程的均温趋势变化和短周期日变化进行分解，并采用一阶傅里叶级数对其拟合得到均匀温度时程表达式，见式(13)，得到轨道结构年均匀温度为21.38 ℃，年均温的变化幅值为11.3 ℃；对均匀温度波动样本进行统计，得到轨道结构均温波动正负温差最值分别为8.27、-8.69 ℃。

(3)截面Ⅱ从上到下各测点的波动变化范围逐渐减小并趋于稳定，通过对轨道结构日温差最值统计样本进行分析，得出截面Ⅱ最大正温差的实测值与估计值分别为18.8、26.8 ℃，采用指数形式对结构竖向温度梯度实测最值与估计值进行拟合，可为无砟轨道结构温度作用取值提供参考。