基于ARMA-BP 组合模型的装备故障率预测方法*

徐 达，周 诚，关 矗，王小闯

（陆军装甲兵学院兵器与控制系，北京 100072）

0 引言

装备故障率是装备维修性验证试验中进行故障样本分配的主要依据，故障率预测结果是否准确直接影响维修性验证试验结果的可信度。目前，普遍采用能充分利用装备在服役期间的故障率数据，真实反映出装备故障率水平的时间序列预测方法预测装备故障率。

针对故障率时间序列预测问题，目前常用的方法有人工神经网络、支持向量机、ARMA 预测法、指数平滑法等。如文献［1］将反向传播BP 神经网络模型应用到火炮身管寿命预测上，有效提高了预测结果精度；文献［2］利用支持向量机良好的非线性时间序列预测能力，实现了对装备费用的预测；文献［3］提出了一种基于ARMA 模型的故障率预测方法，并以使用阶段的波音飞机为例进行故障率预测，结果表明该方法有良好的预测能力；文献［4］建立了一种基于指数平滑法的预测模型，实现了对装备维修器材需求量的准确预测。由于每种方法都具有一定的局限性，以上采用单一方法预测装备故障率，难以实现较高精度的预测。研究表明，相对于单一预测模型，组合预测模型预测能力更强［5］。本文基于组合预测的思想，提出了一种基于ARMA-BP 组合模型的装备故障率预测方法，综合ARMA 模型处理线性时间序列数据和BP 模型处理非线性时间序列数据的优点，有效弥补了单一预测模型的不足，从而实现更高精度的装备故障率预测。

1 单一模型的建立

1.1 ARMA 模型

自回归滑动平均模型（简称ARMA）常用于平稳时间序列分析预测问题，建模流程如图1 所示。

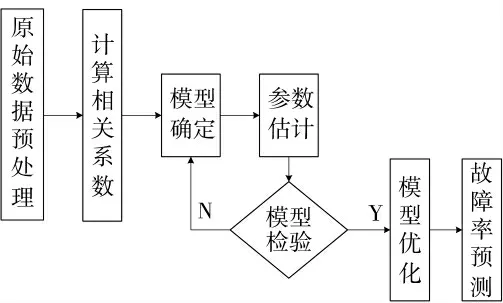
图1 ARMA 模型建模及预测流程

1）预处理原始数据、计算相关系数并确定模型，如表1 所示［6］。

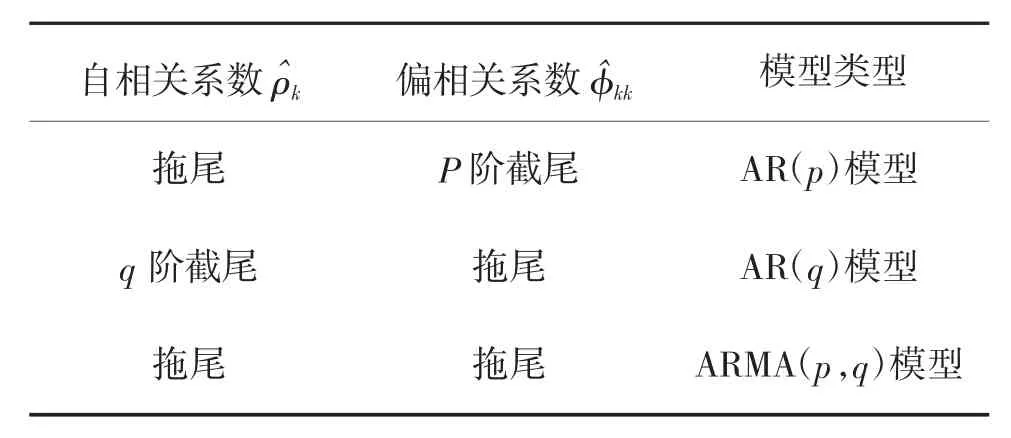
表1 模型类型及阶数确定

2）估计参数，求出模型参数。

3）模型检验，判断模型是否适用于样本故障率数据，进而优化模型。

4）故障率预测，通常预测精度与数据量成正比，数据越多，预测精度越高。

ARMA（p，q）模型结构为：

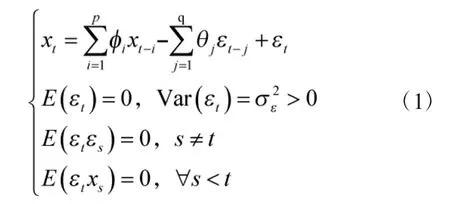
ARMA（p，q）模型具有两种变形结构：

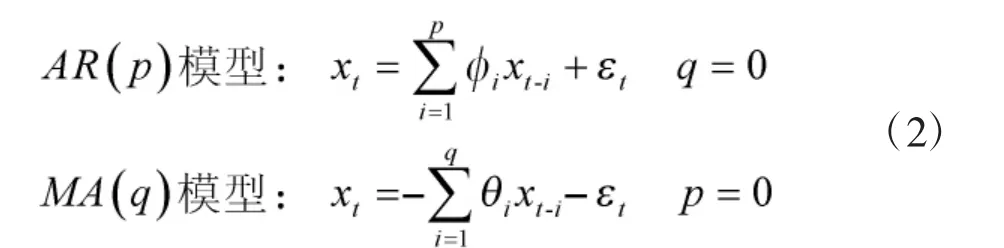
1.2 BP 神经网络模型

误差反向传播网络（简称BP）在解决非线性时间序列问题时，具有学习能力强、结构简单、自操作性好等优点［8］。只要合理选择隐含层节点个数，3 层结构的BP 模型可以处理任意复杂的非线性输入和输出关系的问题，如图2 所示。

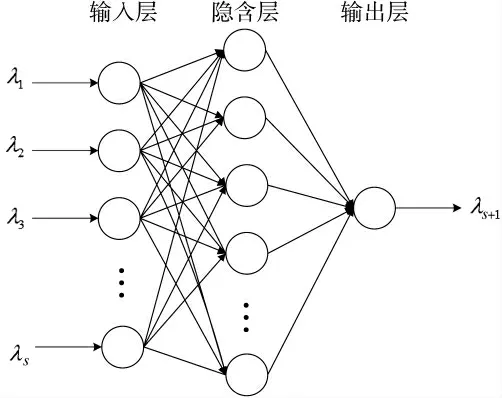
图2 3 层结构的BP 神经网络

确定隐含层节点个数方法主要有经验法和试验法［9］。经验法公式为：

采用累计故障率方法生成训练样本，假设有n个样本数据，将前s 个数据作为输入，第s+1 个数据作为输出，可以分为n-s 组，如表2 所示。为保证较高的预测精度，s 通常取6～12［10］。

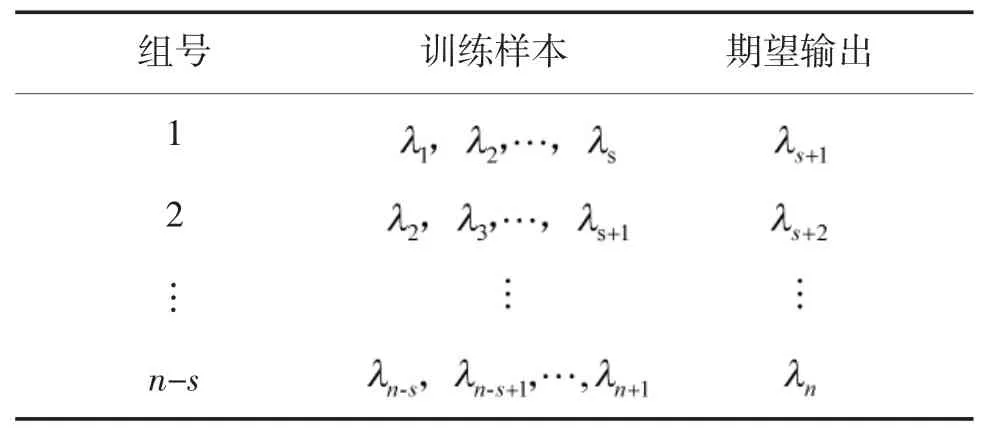
表2 故障率分组

2 ARMA-BP 组合模型的建立

将处理线性和非线性时间序列问题的两种或两种以上单一预测模型有机组合进行预测，能最大限度利用有用信息，弥补单一模型的不足，提高预测精度［11］。基于组合预测的思想，采用加法集成法构建了ARMA-BP 组合预测模型，并利用方差倒数法确定了ARMA 模型和BP 模型的权重。

设ARMA 模型、BP 模型故障率预测结果分别为f1、f2，则组合模型预测结果f 为：

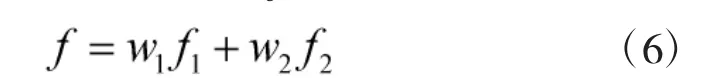
3 仿真实例与结果分析

以某型装甲装备维修性试验为例，已知该装备在2013 年-2018 年服役期间的故障率如表3 所示，统计时间间隔期为一个季度。以前5 年的故障率为基本数据，应用ARMA 模型、BP 模型和AR MA-BP 组合模型分别预测2018 年4 个季度的故障率，并与真实值对比分析误差。

表3 某型装甲装备故障率值

表3 某型装甲装备故障率值

时间2013 年第一季度2013 年第二季度2013 年第三季度故障率images/BZ_88_783_1806_805_1836.png0.061 6 0.075 6 0.093 4时间2015 年第一季度2015 年第二季度2015 年第三季度故障率images/BZ_88_1453_1806_1474_1836.png0.287 4 0.302 6 0.315 6时间 故障率images/BZ_88_2122_1806_2144_1836.png2017 年第一季度 0.327 8 2017 年第二季度 0.345 2 2017 年第三季度 0.357 5 2013 年第四季度 0.162 2 2015 年第四季度 0.336 8 2017 年第四季度 0.347 4 2014 年第一季度 0.238 7 2016 年第一季度 0.355 7 2018 年第一季度 0.336 3 2014 年第二季度 0.217 6 2016 年第二季度 0.314 2 2018 年第二季度 0.352 8 2014 年第三季度 0.196 2 2016 年第三季度 0.268 2 2018 年第三季度 0.367 4 2014 年第四季度0.238 6 2016 年第四季度0.296 7 2018 年第四季度 0.379 2

3.1 ARMA 模型仿真分析

采用EVIEWS 软件处理故障率样本数据，结果如图3 所示。

图3 故障率样本数据变化趋势图

零均值化处理故障率数据并作自相关性分析，结果如图4 所示。

图4 样本故障率数据自相关分析图

由图4 可初步确定模型结构为AR（p）模型，分别估计AR（1）、AR（2）、AR（3）、AR（4）的参数，结果见下页表4。

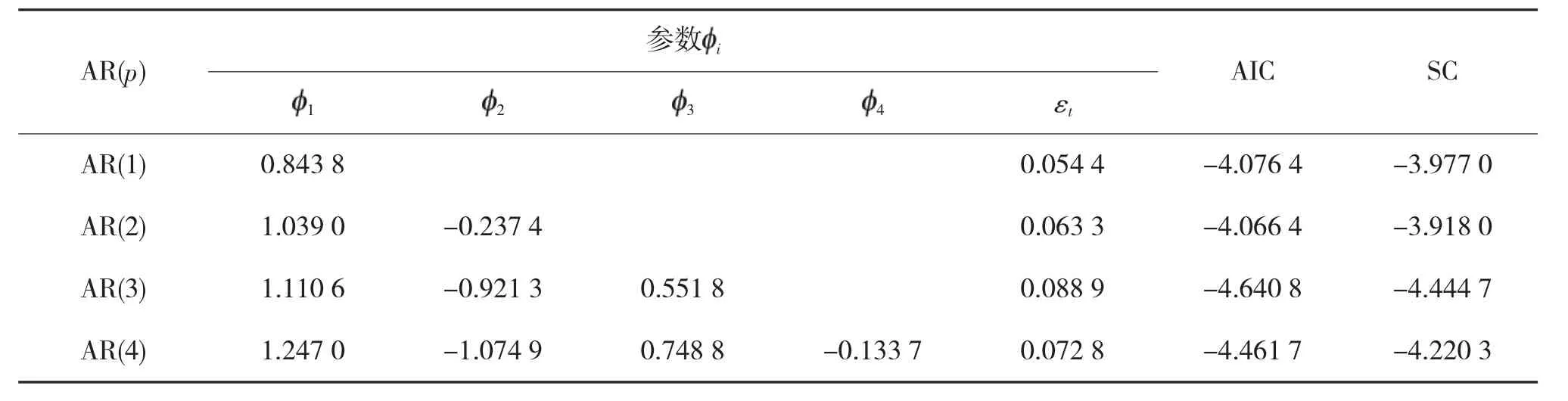
表4 AR（p）模型参数值及AIC 值和SC 值

根据EVIEWS 软件中赤池信息量（AIC）和施瓦兹（SC）取值最小准则，AR（p）模型最佳阶数应为3，根据式（2）可知，AR（3）模型为：

最后，利用式（9）预测2018 年4 个季度的装备故障率。

3.2 BP 神经网络模型仿真分析

根据装备故障率数据，按照第1.2 节中的方法建立如表5 所示训练样本，取s=8。

利用Matlab 训练BP 模型，已知输入、输出的神经元个数分别为8 和1，输入层到隐含层、隐含层到输出层的传递函数分别采用tansig 函数和logsig 函数，经过反复试验，确定隐含层神经元个数为10，学习函数采用基于L-M 算法的trainlm 函数，装备故障率预测精度最高，收敛速度最快。BP 模型寻优过程结果如图5 所示，最优代数为22 代之后。

图5 BP 神经网络寻优过程

最后，利用训练完成后的BP 模型预测2018 年4 个季度的装备故障率。

3.3 ARMA-BP 组合模型仿真分析

根据式（7）、式（8）计算出，ARMA 模型和BP 模型的权重分别为0.4 和0.6，利用ARMA-BP 组合模型可预测2018 年4 个季度的装备故障率。对比3种模型的故障率预测结果如下页表6 所示。

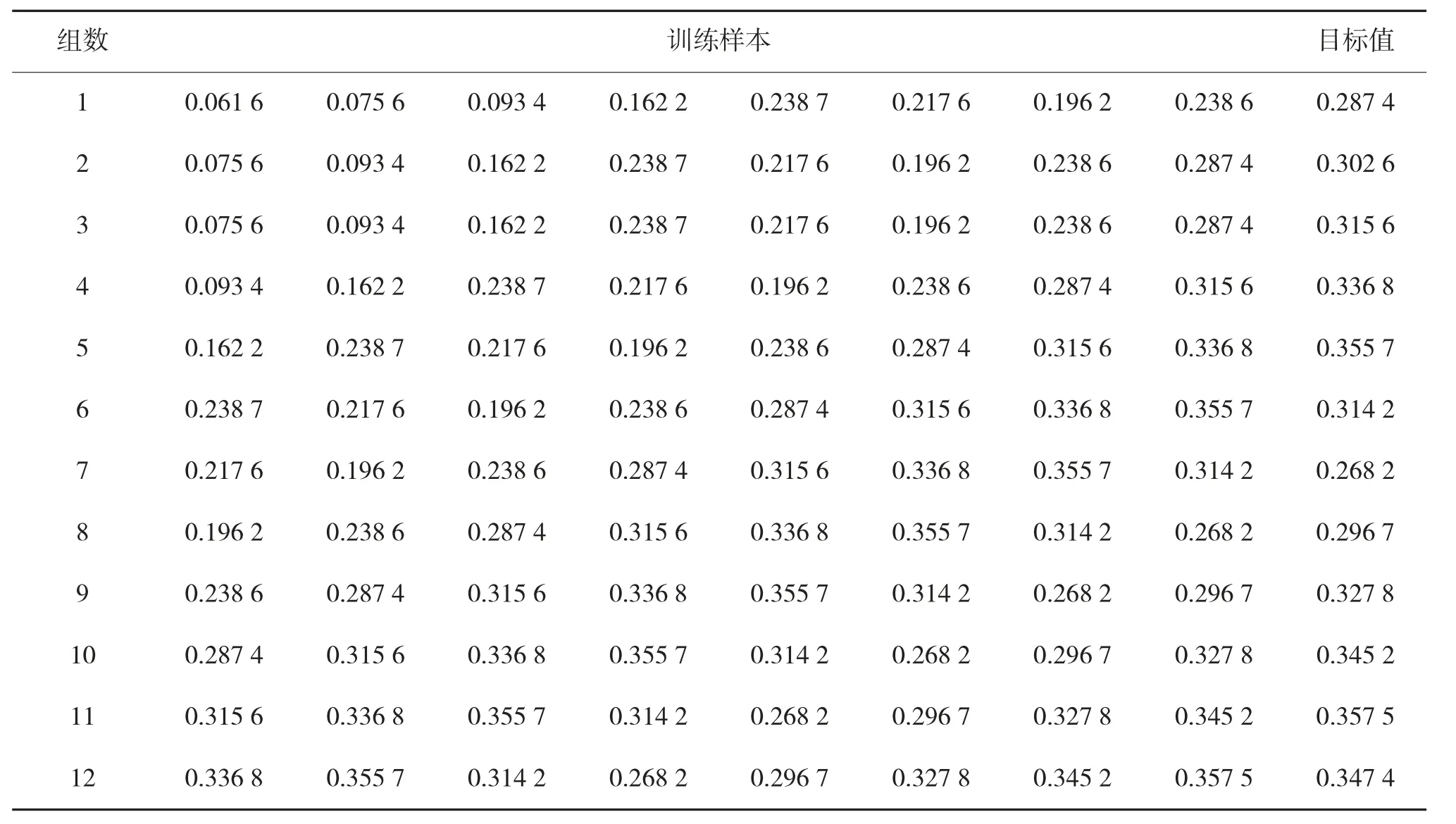
表5 BP 神经网络训练样本

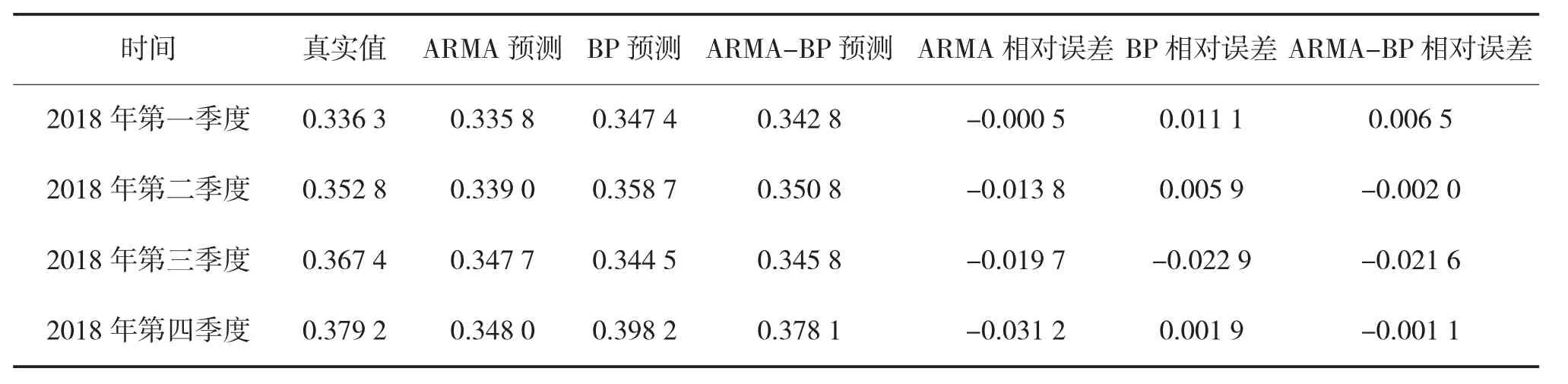
表6 3 种模型装备故障率预测值误差对比

由表6 可知，对比BP 模型和ARMA 模型预测结果，前者相对误差总体比后者小，表明BP 模型预测结果更接近装备故障率真实值，预测误差相对较小，所以在组合模型中，BP 模型所占权重较大。同时，3 种模型的装备故障率预测结果相对误差总体排序为：ARMA-BP 组合模型＜BP 神经网络模型＜ARMA 模型，结果表明本文所提方法相对于单一预测模型，装备故障率预测精度最高。

4 结论

本文针对装备故障率预测问题，提出的一种基于ARMA-BP 组合模型的预测方法，能充分结合ARMA 模型处理线性时间序列问题和BP 神经网络模型处理非线性时间序列问题的优点，克服单一预测模型的局限性，结合装备实例验证了所提方法相比于单一预测模型装备故障率预测精度高，表明该方法在预测装备故障率领域合理可行，对开展装备故障率预测工作具有较高的参考价值。