对于漏斗拾起乒乓球现象的受力及运动研究
2021-02-02许英特王心华李可意赵瑞丰
许英特,王心华,李可意,赵瑞丰
(兰州大学 a.萃英学院;b.物理学国家级实验教学示范中心,甘肃 兰州 730000)
漏斗拾起乒乓球现象在物理教学中经常被提及,并用来解释伯努利方程[1].相似的现象已经在漏斗中流体是水的情况下有过研究[2],结论是当水流量大于40 L/s、漏斗开口角度在30°~45°时,现象较明显.由伯努利方程解释升力的工作已经有很多[3-5].随着计算流体力学的发展,也可以用数值模拟进行仿真计算[6-7].本文探究了漏斗与漏斗中球的受力情况、运动情况,建立了相关定量唯象理论[8].对现象进行建模并用COMSOL Multiphysics进行数值模拟.
1 变量说明及研究思路
1.1 实验装置及变量说明
向开口向下放置的漏斗中快速“吹”入空气,放在漏斗口附近的乒乓球在适当的区域会被“吸入”漏斗内部,乒乓球不断碰撞漏斗壁.
关于流体在空间中的运动,可用纳维-斯托克斯方程对流场的体积元进行解释[9],但无法描述漏斗内气体整体流动的宏观状态.
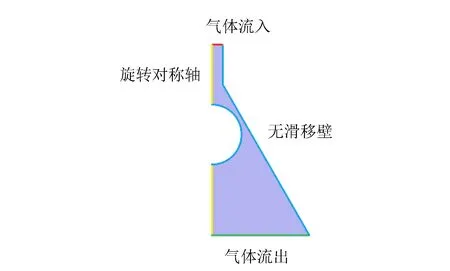
通过预实验发现影响小球被拾起的主要因素有:漏斗半顶角α、气体初始流量Q0、导管半径r.其他的因素(如小球半径R,质量m,空气的各项参数等)也会产生影响,但由于流体的标度相似律,可以利用量纲分析法构造无量纲量,直接探究无量纲量对现象的影响,减少变量个数.实验装置及相关研究参量如图1所示.
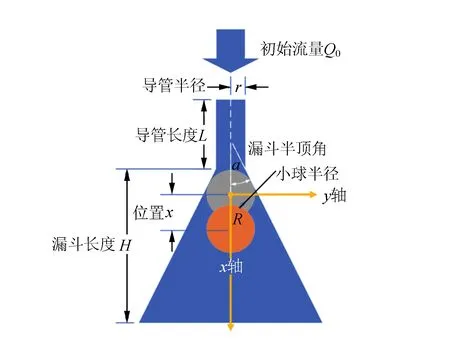
图1 实验装置及参量示意图
由于旋转对称性,小球在漏斗中的位置只需要x,y坐标描述.建立的坐标系为x轴向下为正,球的位置x表示球与漏斗相切的位置向远离漏斗方向移动的距离.
1.2 研究思路与方法
本论文主要研究小球能否被拾起和小球被拾起后在漏斗中的运动情况(包括振幅、振动周期的大小).研究过程始终侧重于实验观测,辅以数值模拟结果,对现象进行总结,最终形成关于该问题的唯象理论.
为研究系统动力学行为,探究小球在漏斗中不同位置所受气流作用力F=f(r,v),也就是小球受周围气流施加的附加压强在表面上的积分.自变量表示,合力至少依赖于小球位置、速度.然而运动小球的受力测定困难,所以假设f(r,v)≈f(r,0),即运动时小球受力可用静止时测定的受力代替.后续实验将表明这一假设是合理的.
本研究中,应用流体的标度相似率,一方面可以减少研究参量的个数,另一方面更接近流体问题的本质.针对此题,当小球满足v=0,希望得出的气流作用力公式为
F=f(α,Q0,r,x,y,R,μ,ρ),
(1)
利用量纲分析,根据Buckingham Pi定理[1],以小球半径R,空气黏度μ,空气密度ρ为基本量,可以等价地将气流作用力的关系式转换为无量纲量的关系式:
(2)
可以发现,需要探究的变量个数减少了.关于基本量的选择:由于涉及到MLT三个量纲,所以基本量的个数应是3个.其中,R是衡量尺寸的特征长度.其余2个基本量选择μ和ρ,是因为这两者在此问题中会产生主要的影响[10].同时,R,μ,ρ在量纲上是线性无关的,构成MLT量纲的一组完备基,可以无量纲化任意相关参量.
2 实验装置及相关物理量测量
2.1 实验装置
如图2所示,实验装置主要由气泵、导管、节流阀、流量计、测力计、漏斗及球、高度游标卡尺组成.为了保证流入漏斗气流的对称性,气流流经的导管竖直布置,并且内径统一,以使气流在进入漏斗前经历长距离的直线运动.相应地,进入漏斗的气流沿径向的流速分布满足泊肃叶分布.

图2 实验装置整体图
漏斗为3D打印制作,材质为树脂,半顶角取值为20°,40°,50°,60°,导管半径r=7.18 mm,壁厚度2 mm.为了拍摄运动视频需要,特制作了透明漏斗,材质为可弯折塑料板.
受力测定采用斯巴拓(烟台)精密机械零部件有限公司生产的SBT970型手持式传感器,配套对应的压力传感器和计算机软件(最小分度可达0.1 gf, 1 gf=9.8×10-3N)来进行受力测定.装置如图3所示,乒乓球通过刚性细杆固连在力传感器上,刚性杆保持竖直,并调整乒乓球静止时力传感器的示数为零.这样设置,乒乓球所受的x轴方向力即为传感器示数值.为了使小球位置稳定,减弱小球振动,小球内填充了沙子以增大惯性.通过这样的结构可以测定小球处于漏斗内某一特定位置时的受力.经过数值模拟分析,细杆对气流影响较小,支撑点球表面的压强也近似为参考压强,因此细杆的影响可以忽略.

图3 测力装置图
2.2 录制小球在漏斗内运动的视频
使用高速摄像机以水平视角对准透明漏斗,由于帧率提高后曝光时间降低,影像亮度降低,所以需要汞灯对小球进行补光.为了便于观察在乒乓球表面做了记号,并且高速摄像机的镜头方向是调节水平的,这样球沿轴线方向的上下运动就对应于影像中的上下运动.
3 实验探究及结果验证
3.1 实验探究
3.1.1 小球静止时的受力分析
先研究小球静止在漏斗中固定位置时,流场达到稳定后,小球受力与位置、各个参量的关系.也就是探究F=f(r,v)在v=0时的情况.为了简单起见,假设球沿轴线运动,即y=0.对于单次受力测定,将小球位置固定,在气流稳定后,使用计算机在一段时间内对传感器受力进行采样,可以得出受力的平均值和标准差,如图4是对受力进行采样的示例.
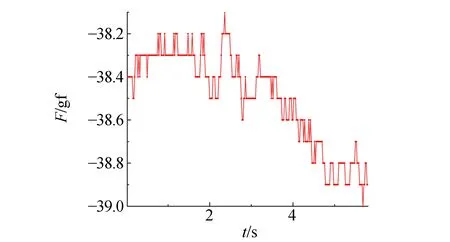
图4 单次受力测定采样结果
可以观察到,在流场达到稳态后,力传感器显示小球受力在38~39 gf.受力的涨落是由湍流引起.仍可以发现受力在不断变大,这是因为固连的小球在气流作用下位置逐渐有微小的偏移.
3.1.2 受力曲线
再以一定步长改变x值(小球在漏斗中的位置),测定一定范围内的F-x关系,如图5是某一特定情况下测定的受力曲线.
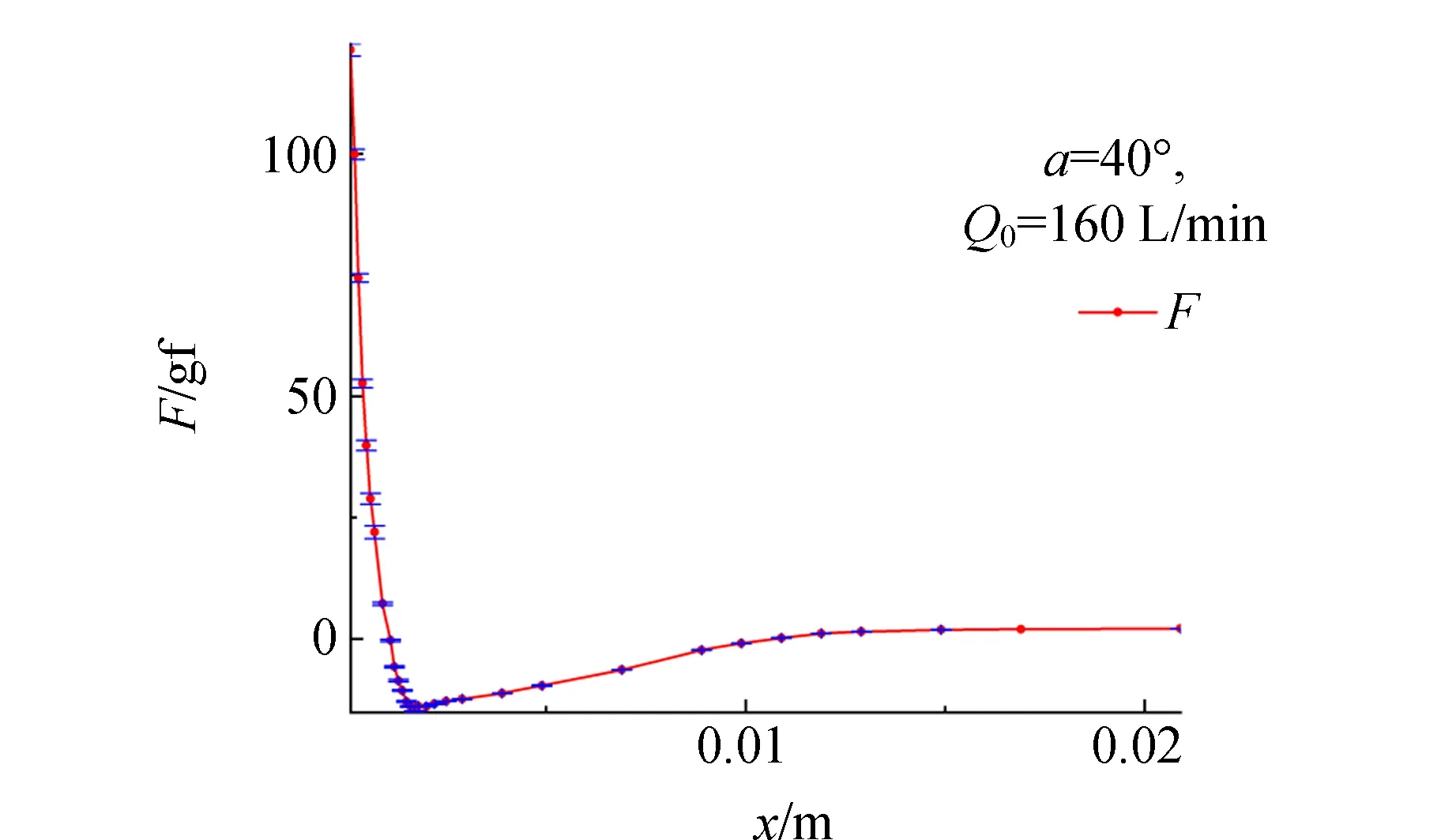
图5 受力曲线示例
观察该受力曲线可以发现,小球的受力分为3个阶段.
第一阶段:小球离漏斗较近(x<1.5 mm),小球受气流作用力的值为正,即气流的合力向下,且随距离增大而迅速减小,这与常识相符.
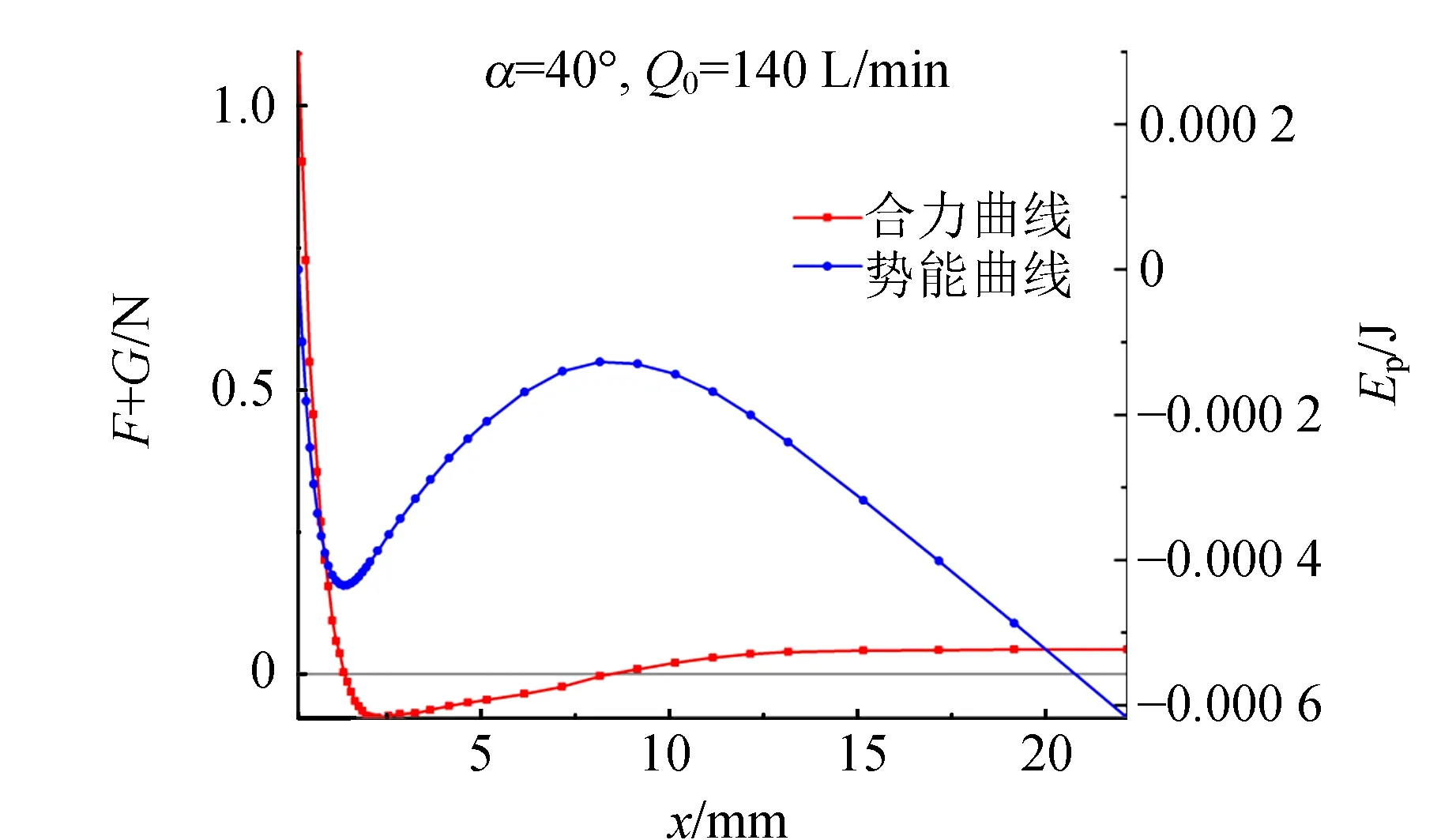
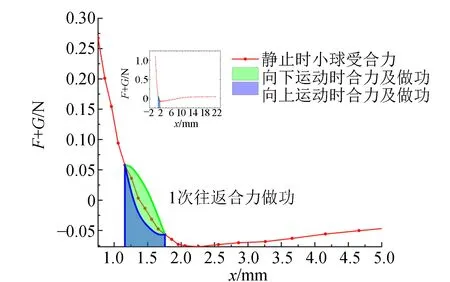
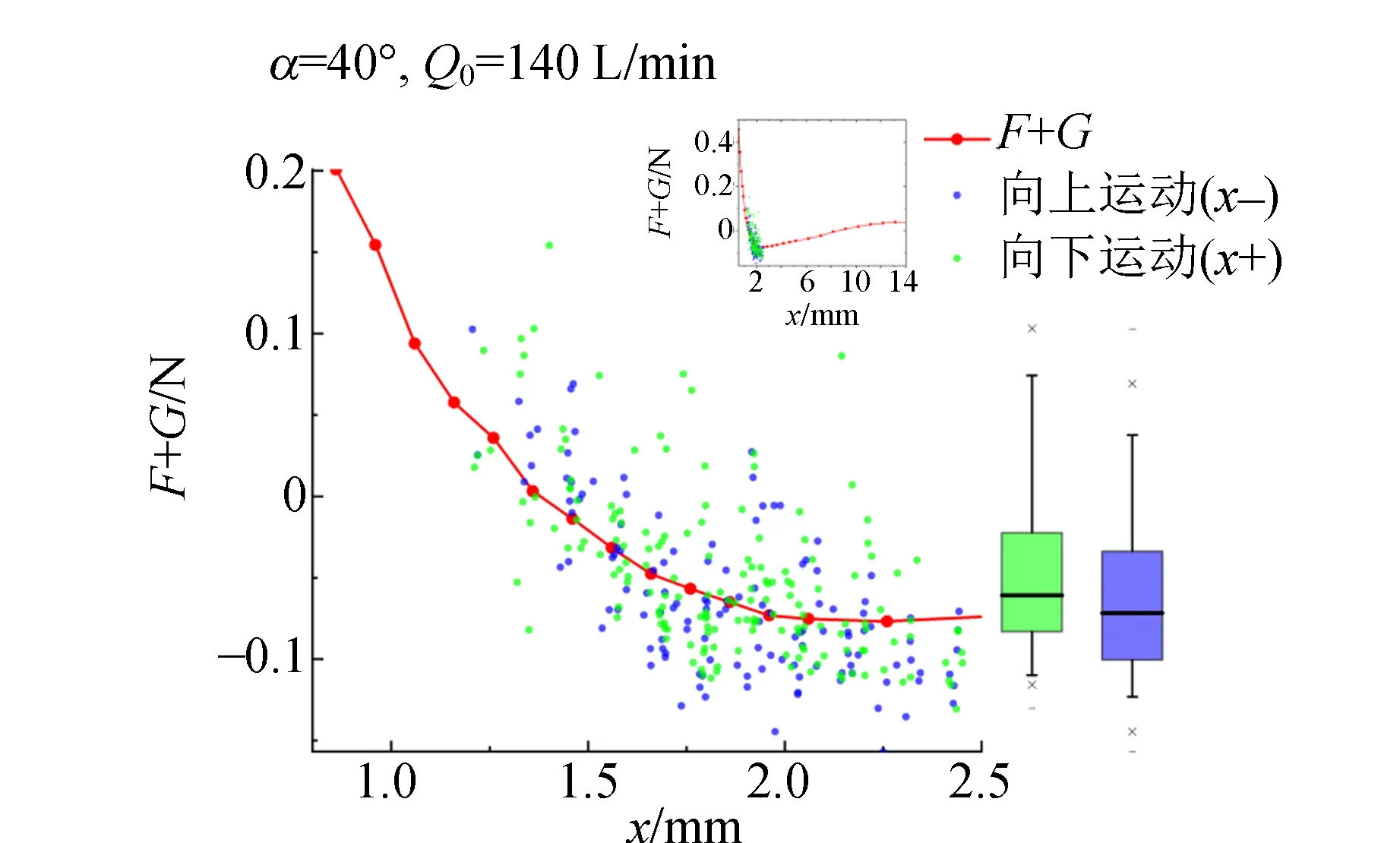
第二阶段:小球离漏斗一定距离(1.5 mm 第三阶段:小球离漏斗较远(x>10 mm),气流作用力逐渐稳定在某正的值,合力向下. 3.1.3 受力曲面 (a)α=40° 3.2.1 受力曲线的数值模拟验证 在COMSOL中建立与实验条件对应的模型,使用数值模拟的方法辅助分析小球静止时流场的情况.数值模拟设置如下: a.物理场模型:方程使用RANS方程(雷诺数平均纳维-斯托克斯方程)的k-ω模型 b.计算流场达到稳态的情况 c.入口处采用流速的泊肃叶分布 d.参考压强采用实际实验室气压81.28 kPa 几何建模及边界条件如图7所示. 在拓展课的总结与展望部分,学生提出了如下问题:本实验中检测的微生物类型有限,不能说明铁皮石斛具有广谱的抗菌功能,被检微生物的类型有待增加;铁皮石斛中的抗菌的有效成分有待明确,有条件的情况下可以把多糖、生物碱和氨基酸类物质分离,分别进行抑菌实验。后续研究中,可以尝试将铁皮石斛匀浆液添加到相应免疫细胞的培养基中,观察其对免疫细胞数量及活性的影响。从本案例中,可发现,高中生已经具备质疑、查阅资料、设计实施实验、思考与总结的能力,教师应根据学生的发展特征与需求提供支持与条件,助力学生核心素养的发展。 图7 COMSOL几何建模及边界条件 由于旋转对称性,建模时采用二维旋转对称的结构.其中漏斗内部除去小球占据的空间,即为求解流场的空间. 对COMSOL模拟的参量值进行设置,使模型与实验时一致.将相同参量下模拟与实验得到的受力曲线进行比对,如图8所示,通过比对发现,COMSOL数值模拟的结果与实验虽有定量有差别,但定性是一致的[11].定量差别的原因在于在建模时,存在一些未被考虑的因素. 图8 实验结果与模拟结果比较图 对半顶角为不同值时进行建模、计算,仔细观察在不同半顶角下,小球处于不同位置时(流场达到稳态)的流线图,可以发现流场状态分为不同阶段.当小球离漏斗较近,气流沿着小球与漏斗相切的狭缝高速射出,形成射流.随着距离增加,流场开始向绕过小球流动的情况过渡.最终,吹入的气流全部绕过小球流动. 由图9可知,流线的不同阶段对应了受力曲线的不同阶段.比如当小球离漏斗较远时,吹入气流全部绕过小球流动.因此,小球附近流场与小球位置无关,趋于稳定,对应了受力曲线第3阶段时气流作用力稳定在某正值. 图9 半顶角α分别为20°,30°,40°,50°时,小球稳定在不同位置的气流流线图 3.2.2 小球被拾起的原理解释 模拟结果验证了实验结论是正确的,所以利用COMSOL模拟给出的流线图(如图10所示),可以从宏观上描述小球被拾起的原理.在一段流管中存在关系[12-13]: p静+p动=p总 其中p静为流体静止时内部的压强,p动与动能相关,p总与总能量相关.对于理想流体的情况,p总为恒定值,则该式实际上就是伯努利方程.在实际情况下,由于液体黏滞阻力的存在,则总压沿路程减小. 在此问题中,气流作用力主要由正压区、负压区2部分组成.被吹入漏斗的高速气流在小球上方被阻挡,动压转化为静压,形成正压区,对小球施加向下的力.气流在小球与漏斗相切处又高速射出,动压变大,静压变小,以至于表压为负(表压=静压-参考压),形成负压区. 在图10(a)的情况中,正压区占主导,合力向下,F>0,对应受力曲线第一阶段.在图10(b)的情况中,负压区占主导,合力向上,F<0,对应受力曲线第二阶段,这是使小球被拾起的原因.在图10(c)、(d)情况中,小球附近流场趋于稳定,受力稳定在一个正值.其中图10(d)对应的流线情况是流线不再贴着漏斗壁、再形成大的涡流,而是贴着乒乓球表面.这种流线贴近于凸起表面的现象是很明显的科恩达效应. 图10 COMSOL模拟流线图 总的来说,小球被拾起的原因,可以解释为流速大,压强小的负压区占据主导的伯努利效应. 实验室环境下ρ =1.045 kg/m3,μ =1.81×10-5Pa·s,乒乓球半径测量为R=2.00 cm. 3.3.1 半顶角α的影响 经过实验发现,半顶角较小时,拾起小球的x范围较大,但气流作用力的绝对值较小.半顶角较大时则相反,将小球拾起的x范围较小,但气流作用力的绝对值较大.实验结果如图11所示. 图11 半顶角对小球受力的影响 3.3.2 初始流量Q0 实验发现,初始流量Q0只影响气流作用力的绝对值大小,并不改变受力曲线形态.当初始流量越大,小球受气流作用力的向上、向下的力都会变大.值得注意,气流作用力为零的点是与初始流量无关的.实验结果如图12所示. 图12 初始气体流量对小球受力的影响 3.3.3 导管半径r 与的影响类似,在实验探究范围内导管半径的大小只影响气流作用力绝对值的大小.导管半径越小,气流作用力的绝对值越大.数值模拟结果如图13所示. 图13 导管半径对小球受力的影响 对小球被拾起后的特定情况(α=40°,Q0=140 L/min,r=7.18 mm)使用高速摄像机拍摄视频,帧率为1 000 s-1.将视频导入Tracker软件内描点,得到一段时间内小球位置(x,y)随时间的变化关系,如图14所示. 图14 Tracker描点图 在运动过程中,小球在漏斗内沿轴向、垂直轴向振动.由于实验的偶然因素(如气泵不稳定等),小球有时会受到扰动.图14采用的数据中,在0.20 s 3.4.1 对小球运动的解释 为解释小球的振动,假设小球在运动时的受力等于静止在相同位置、流场稳定时的受力,且小球受x轴方向作用力与在轴线上的情况相同,即 F(r,v)=F(x,0), (3) 因为假设气流作用力只与位置x有关,则该力可以视为保守力,对特定情况的受力曲线进行数值积分,求解出其势能,发现在气流作用力为零的第一个点存在一个势阱,当小球总能量低于势阱,就被限制在一定区域上下振动,如图15所示. 图15 小球受力曲线、势能曲线示例 根据相同参数下的静止时受力,及上述假设,可以根据插值法,得到小球在漏斗内不同位置运动时受力的结果.根据不同位置受力,结合牛顿第二定律,就可以运用数值方法求解出小球沿轴向运动的情况.在图16(a)中,上图灰色部分即数值模拟时设置的振动区域(由于假设气流作用力为保守力,这个振动区域是由初始释放位置的设置决定的).在图16(b)中,黑色部分为数值模拟推演的结果,红色部分为实验测定结果. 图16 小球振动的理论计算与实验结果对比 在保守力场中,振幅、周期与初态有关.保守力场平衡点,即对应势能的极小值点.物体在其附近振动,则越远离势能极小值点,势能越大.显然物体在不同位置释放,其初态具有的机械能不同,运动到另一端势能相等的位置,距离不同,振幅也相应改变.关于周期,受简谐力的物体周期不随初态改变,但受一般的保守力而振动的物体,在振幅较大时,周期也依赖于初态. 通过以上研究发现,根据静止时的受力推演出的小球运动,与实验测定符合较好.振动的幅度和频率是符合的,部分波形重合,并且当t>0.2 s时不重合的部分实际上是2者存在一个相位差.所以用静止时受力,近似认为是小球运动时受力的假设是合理的. 3.4.2 振动状态与初态无关的解释 如果假设气流作用力为保守力,小球的运动与初态有关.而实验显示,小球的运动会很快达到一个与初态无关的稳态.这是因为气流作用力并非完全是保守力,小球的振动状态存在一个稳定平衡(这一平衡状态是指小球能量损益的平衡,即在小球上下振动一次的过程中,会因为与漏斗壁碰撞而损失能量,因为气流作用力做功而获得能量.小球会稳定在损失和获得能量平衡的振动状态),偏离平衡的振动状态时,运动会向平衡状态迁移.图17是对气流力做功原理的猜想. 图17 小球运动时能量损益理论示意图 通过Tracker处理后的运动数据,结合插值代替导数的近似,可以得到小球运动过程中在不同位置的加速度的散点图,其中向下运动(x增大)的情况点为绿色,向上运动(x减小)的情况点为蓝色,如图18所示.统计2种情况下加速度的分布,做出箱线图,发现实验结果与球静止时测定的受力曲线相符,且与气流做功的猜想一致. 图18 不同方向运动的受力情况统计 通过实验、理论、数值模拟结合的方法,建立了唯象理论对漏斗拾起乒乓球现象进行解释.利用流体标度相似律,探究了不同参数对小球静止受力、能否被拾起的影响,使研究具有一定普适性.使用受力曲线、受力曲面对将小球静止时受力进行分析,按照小球从靠近到远离漏斗,将受力分为3个阶段,并将被拾起的原因解释为伯努利效应.唯象理论也成功地描述了小球的运动,证实小球在运动时受气流的作用可以近似按静止在同一位置,流场稳定时的受力来计算.解释了振动存在唯一稳态的原因是能量损益平衡.
3.2 COMSOL Multiphysics数值模拟及实验结果的验证与分析
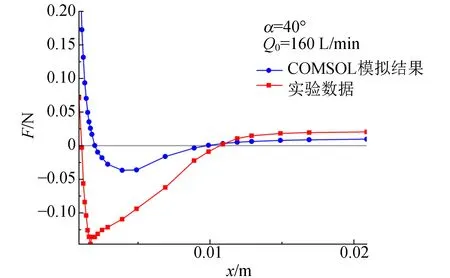
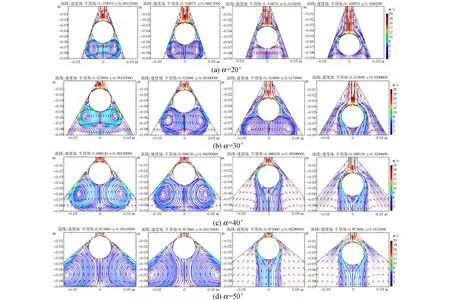
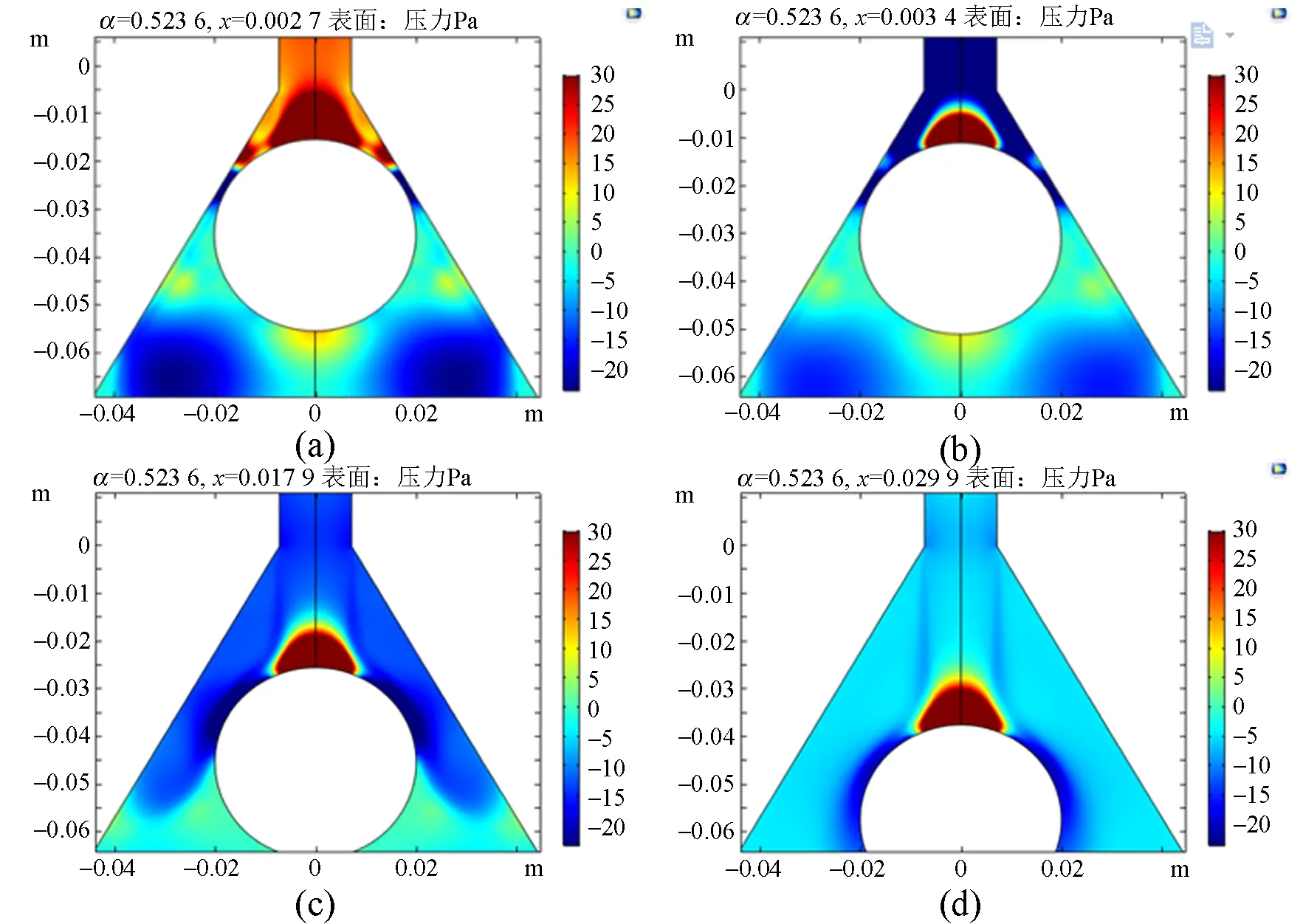
3.3 变量对气流作用力的影响
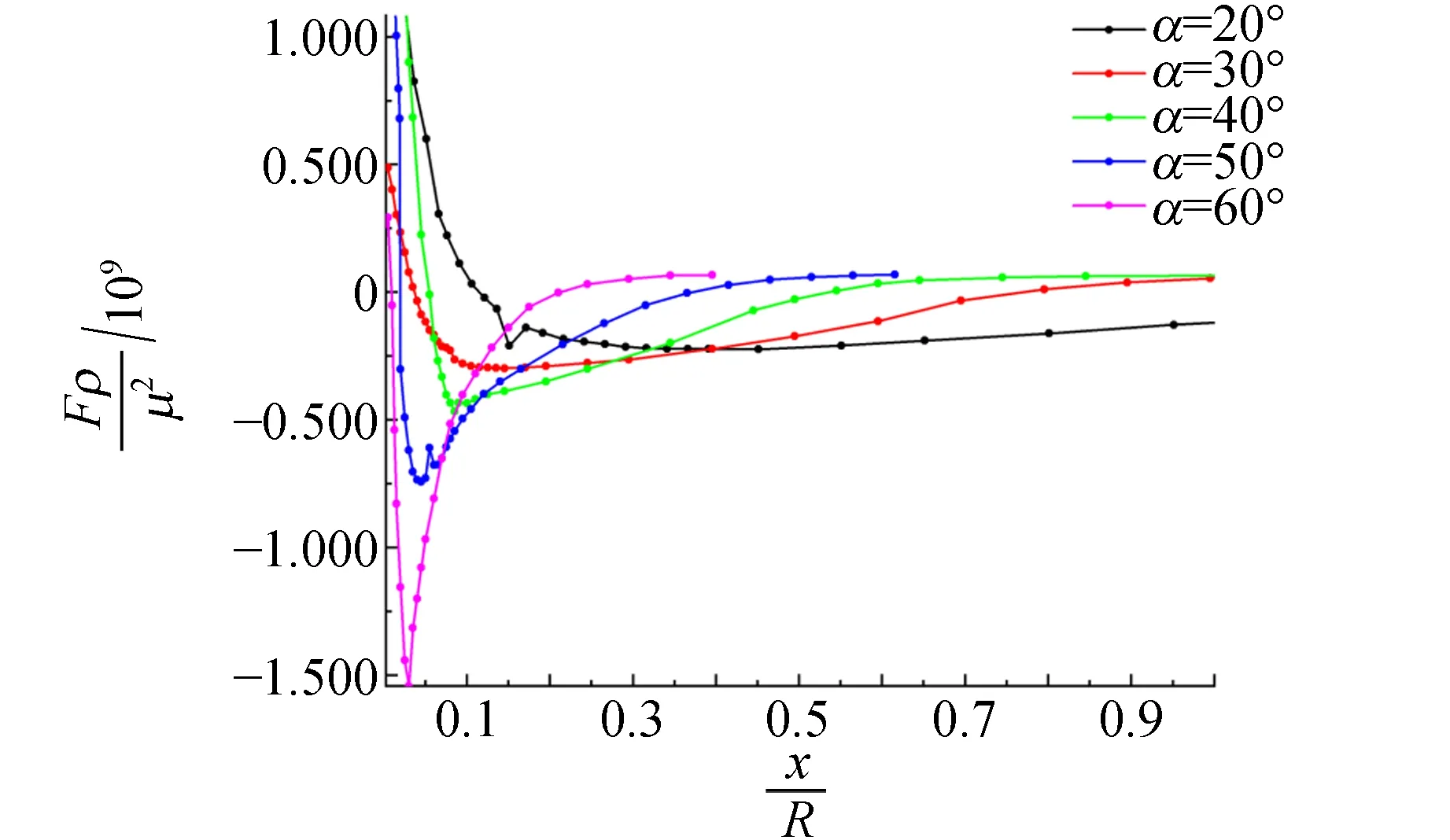
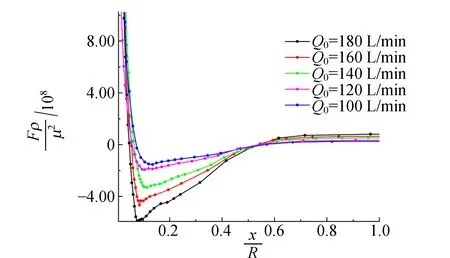
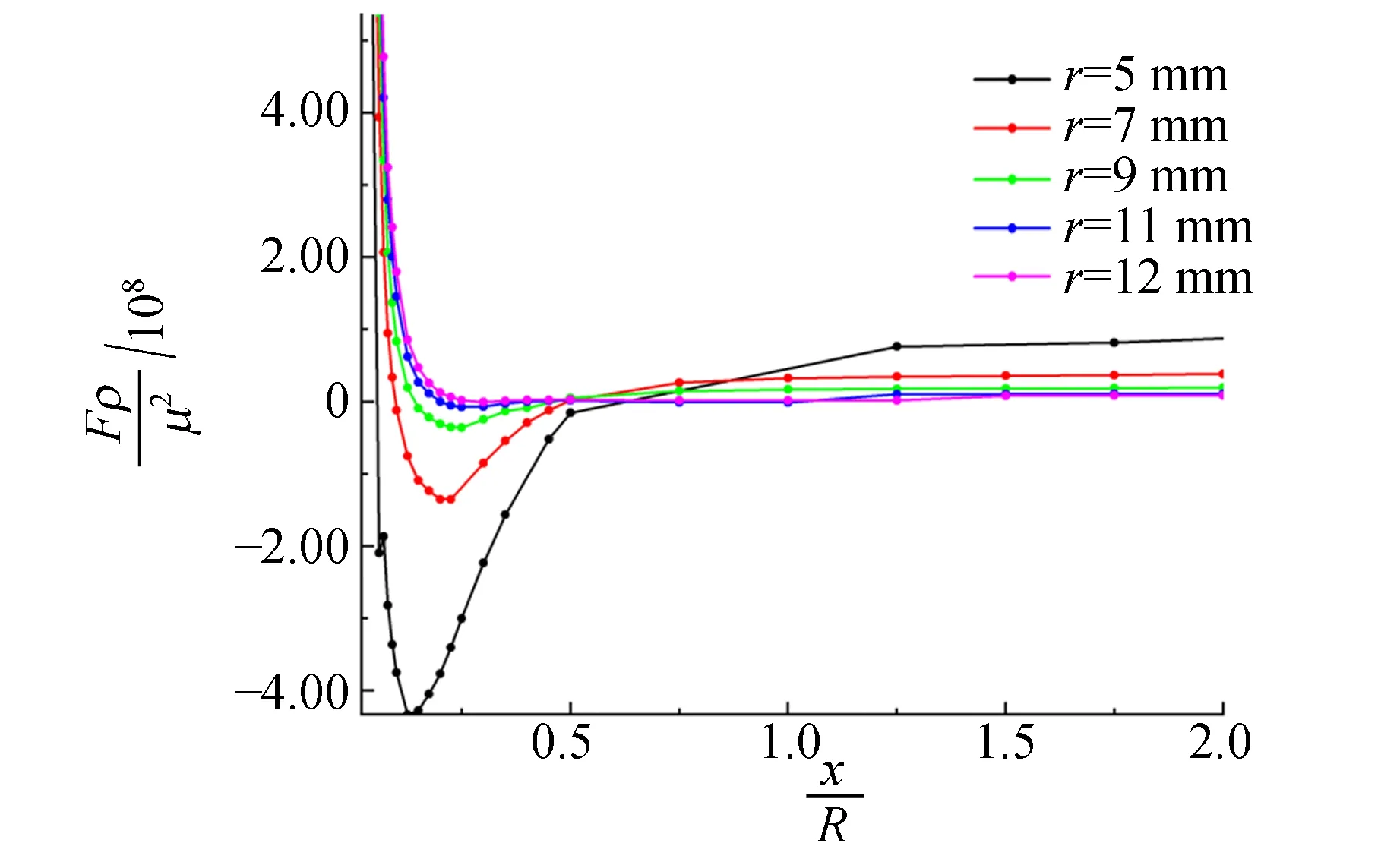
3.4 拾起后小球运动的研究
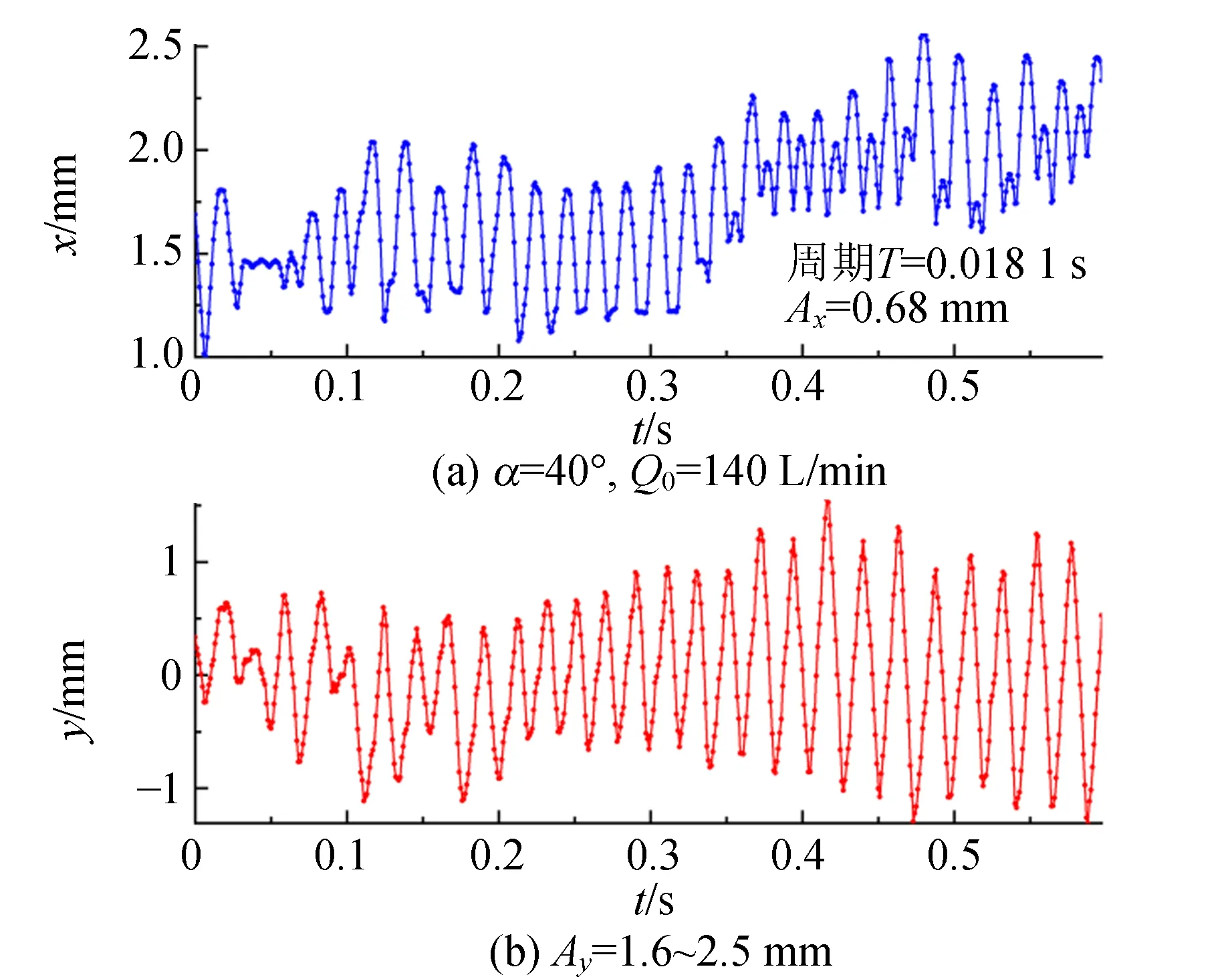

4 结 论
