基于变换光学的隐身衣设计

李恒一，张 权，王中平，赵 伟，郑 虹，朱 玲，张增明

(中国科学技术大学 物理学院，安徽 合肥 230026)

2006年，Pendry等提出了变换光学理论，应用这一理论，可以精确控制电磁波传输的路径[1].变换光学的理论是：利用麦克斯韦方程组在坐标变换下的形式不变性[2](只考虑电磁场关于空间的变换)，通过空间坐标变换来推导介质在现实物理空间上的介电常量和磁导率张量等参量，从而根据这些参量设计具有特殊功能的介质.变换光学建立了空间坐标变换与材料参量改变之间的对应关系，可将复杂的电磁计算问题转换为较简单的空间坐标变换问题，为人类控制电磁波的传播特性提供了理论指导并拓展了新的研究思路.科研人员使用变换光学的方法设计了各种变换光学器件，比如隐身斗篷[3-4]、天线[5]、电磁集中器[6]、电磁波旋转器[7]、透镜[8]等，且很多变换光学器件在实验上已得到了验证[9-10].

本文介绍了麦克斯韦方程组在坐标变换下形式不变性，基于变换光学设计隐身衣的设计思路，并通过COMSOL Multiphysics仿真软件仿真二维圆柱形、椭圆柱形、正方形的隐身衣.将变换光学的理论引入本科物理实验，有利于激发本科生的科学研究兴趣，培养学生的创新能力，提高科研技能等综合实验素质.此外，本文模拟仿真的实验内容亦适用于作为远程教学的课程，丰富教学模式.

1 麦克斯韦方程组在坐标变换下的协变性

麦克斯韦方程组在坐标变换下形式保持不变[11]，这里进行空间变换的区域是无源的，因此麦克斯韦方程组在原空间的表达形式为

×E-jωμH=0,×H+jωεE=0.

(1)

介电常量ε和磁导率μ是与位置坐标有关的函数，原直角坐标系的坐标是x(x1,x2)，新的扭曲坐标系的坐标是x′(x1′,x2′)，如图1所示.麦克斯韦方程组在新坐标系下变为

(a)直角坐标系 (b)扭曲坐标系

′×E′-jωμ′H′=0,′×H′+jωε′E′=0,

(2)

其中

E′(x′)=(ΛT)-1E(x)，H′(x′)=(ΛT)-1H(x),

(3)

雅克比变换矩阵定义为

(4)

将式(2)进一步展开有

(5)

从而只需要证明

(6)

式(6)在正交坐标系是显然成立的，而在一般的曲线坐标系中，亦可以通过张量相关知识进行证明.因此证明了麦克斯韦方程组在坐标变换下的形式不变性，并可以根据式(3)设计和计算变换介质的介电常量和磁导率.值得注意的是，以上情况成立的前提是物体的运动速度远远小于光速.

2 设计思路

变换光学的理论是：利用麦克斯韦方程组在三维坐标变换下保持形式不变性，通过空间坐标变换来推导介质在现实物理空间上的介电常量和磁导率张量等参量，从而根据这些介电参量设计出具有特殊功能的介质.该介质也因此称作变换介质.下面以圆柱形隐身衣为例，进行变换介质的设计.

设计思想如图2所示，原空间光线沿平直的自然空间直线传播，(b)空间为设计的变换空间，其空间网格是变形扭曲的.在二维平面上看(z方向无限长)，(a)空间到(b)空间的变换是在拓扑上把原点胀开变成了小圆的周边，把原本大圆的空间区域压缩到圆环区域中.在原空间中光线沿着光程最短的直线传播，在变换空间中光线则绕过了小圆的区域沿着曲线传播.根据麦克斯韦方程组在坐标变换下的形式不变性，使用特殊设计的变换介质取代圆环区域中的空气介质，可以在物理空间中模拟变换空间中的电磁波传播，即电磁波在(c)空间中蓝色变换介质内的传播路径完全等效于电磁波在对应(b)空间中圆环区域空气介质内的传播路径.在实际物理空间(c)中观察，圆环区域电磁波的传播被变换介质弯曲，圆环内部的空间对电磁波而言就是隐形的，可以通过变换空间(b)与原空间(a)的坐标变换关系得到物理空间(c)中变换介质的介电常量和磁导率张量等参量，这就是变换光学的核心思想.

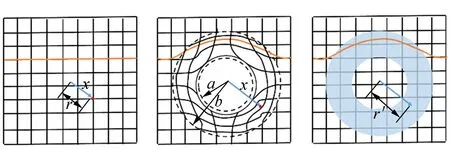
(a)原空间 (b)变换空间 (c)物理空间

3 不同形状隐身衣的设计结果

3.1 二维圆柱形隐身衣

对二维圆柱形隐身衣而言，考虑任意的圆柱形物体，外面包裹1层隐身衣，此隐身衣的横向截面图就是内外半径分别为a和b的圆环.沿z轴方向是恒等变换，可以在柱坐标系中定义如下空间变换：

(7)

计算出雅克比矩阵：

(8)

对应的介电常量和磁导率张量为

(9)

注意物理空间坐标是(r′,θ′).

对入射波是TE波的情况，只需要考虑μr,μθ,μz3个参量即可(TM波则只需要满足εr,εθ,εz)，使用有限元数值模拟软件COMSOL Multiphysics进行模拟计算.

模拟区域为16 μm×9 μm，设置外圆半径b=4 μm,内圆半径a=2 μm，计算区域四周的边界都设置了1 μm厚的完美匹配层，在模拟区域的左侧设置真空波长为365 nm的无限宽TE偏振的电磁波，电场幅值为Ez=1 V/m，在没有损耗的理想情况下(所有材料的折射率虚部为0)，模拟结果如图3所示.

(a)空气中无限宽TM波的场强分布

由图3(a)和图3(b)可以看出，电磁波被隐身衣引导绕过了隐身衣罩住的中心区域，图3(c)和图3(d)对比表明：加入隐身衣后，小铜块的散射完全消失了.值得注意的是，圆环内组成隐身衣的变换介质其介电常量和磁导率参量是张量形式，并且各分量的数值均不是常量，具体与所处位置的坐标有关，且此种形态的隐身衣，介电常量和磁导率的某些分量在隐身衣内边界处的取值趋于无穷大，因此难以在实验上真正实现.如果牺牲一定的隐身效果，则可以设计出实验上能够制作的隐身衣.

再回到式(7)，这是线性的压缩变换，可以采用任意连续可微的函数来定义大圆区域到圆环区域内的映射，最终隐身衣内部的电场分布与映射函数有关，但均不影响隐身效果.以二次函数映射为例，令

计算相应介电常量和磁导率后，给出隐身衣的模拟结果如图4所示.

图4 二次函数映射的圆柱形隐身衣

相比线性映射，电磁波在隐身衣内边界处被扭曲得更厉害，而在外表边界则变化得更趋平缓，此结果与本文的设计思路是一致的.

3.2 椭圆柱形隐身衣

设椭圆柱隐身衣椭圆的长短轴之比为k，外椭圆短轴长为b，内椭圆短轴长为a.由几何关系推导可以写出其坐标变换为[11]

(10)

计算出相对介电常量(相对磁导率数值相同)的参量分别为

(11)

(12)

(13)

(14)

其中,

注意实际物理空间的坐标是x′和y′.可见当k=1时，椭圆退化为正圆，此时介电常量和磁导率张量形式与圆柱形隐身衣的形式完全相同.

不考虑z坐标，在二维平面上考虑椭圆柱形隐身衣的空间变换关系，实质是将二维平面上的外椭圆的中心撕裂成内椭圆的周长，其坐标映射可以如文献[12]经过几何的关系推导出来，也同样可以进行多次空间变换得到.

空间变换的过程是：

1)将二维平面内长轴为kb、短轴为b的椭圆沿短轴y轴方向拉伸k倍，变成半径kb的圆，此时坐标转换是(x,y,z)→(x′,y′,z′),其坐标变换关系是

x′=x,y′=ky,z′=z，

雅克比矩阵Λ1和相对介电常量张量ε1为(空气的相对介电常量为ε0)

(15)

(16)

2)将直角坐标转为极坐标，即(x′,y′,z′)→(r′,θ′,z′)，坐标转换关系是：

雅克比矩阵Λ2和相对介电常量张量ε2为

(17)

(18)

3)类似于圆柱形隐身衣，将半径为kb圆的圆心变换成半径为ka的圆，即(r′,θ′,z′)→(r″,θ″,z″)，坐标转换关系是

雅克比矩阵Λ3和相对介电常量张量ε3为

(19)

(20)

4)将极坐标转为直角坐标，即(r″,θ″,z″)→(x″,y″,z″), 坐标转换关系是

x″=r″cosθ″,y″=r″sinθ″，

雅克比矩阵Λ4和相对介电常量张量ε4为

(21)

(22)

5)将半径ka和kb的圆环沿y″轴方向压缩k倍，变成长轴分别为ka和kb，短轴分别为a和b的2个椭圆围成的椭圆环区域，即(x″,y″,z″)→(x‴,y‴,z‴)，坐标转换关系是

此区域即为以介电常量ε5和磁导率μ5填充的变换介质区域.雅克比矩阵Λ5和相对介电常量张量ε5为

(23)

(24)

注意实际物理空间的坐标是x‴,y‴,z‴.

得到变换介质的相对介电常量张量ε5(相对磁导率张量μ5数值上完全相等)，可见多次坐标变换可以得到正确的结果，与文献[12]复杂的几何推导相比，多次坐标变换的方法思路上更加容易被学生理解，计算上更加程序化，可以通过编程省去复杂的中间过程.

取a=2 μm,b=3 μm，k=1.5,椭圆柱形隐身衣的模拟结果如图5所示.

图5 椭圆柱形隐身衣的场强分布

3.3 正方形隐身衣

基于同样的原理，选择合适的坐标变换关系，可以制作正方形隐身衣.如图6所示，将大的正方形区域变换到大小正方形之间的方形环状区域中，拓扑上需要将原点撕裂为小正方形的四边，大小正方形的边长分别为b和a.可以把大正方形分割为4个大三角形，例如图6中的三角形阴影区域.把所有阴影部分的坐标点一一映射到阴影部分内部的梯形区域中，坐标变换关系为

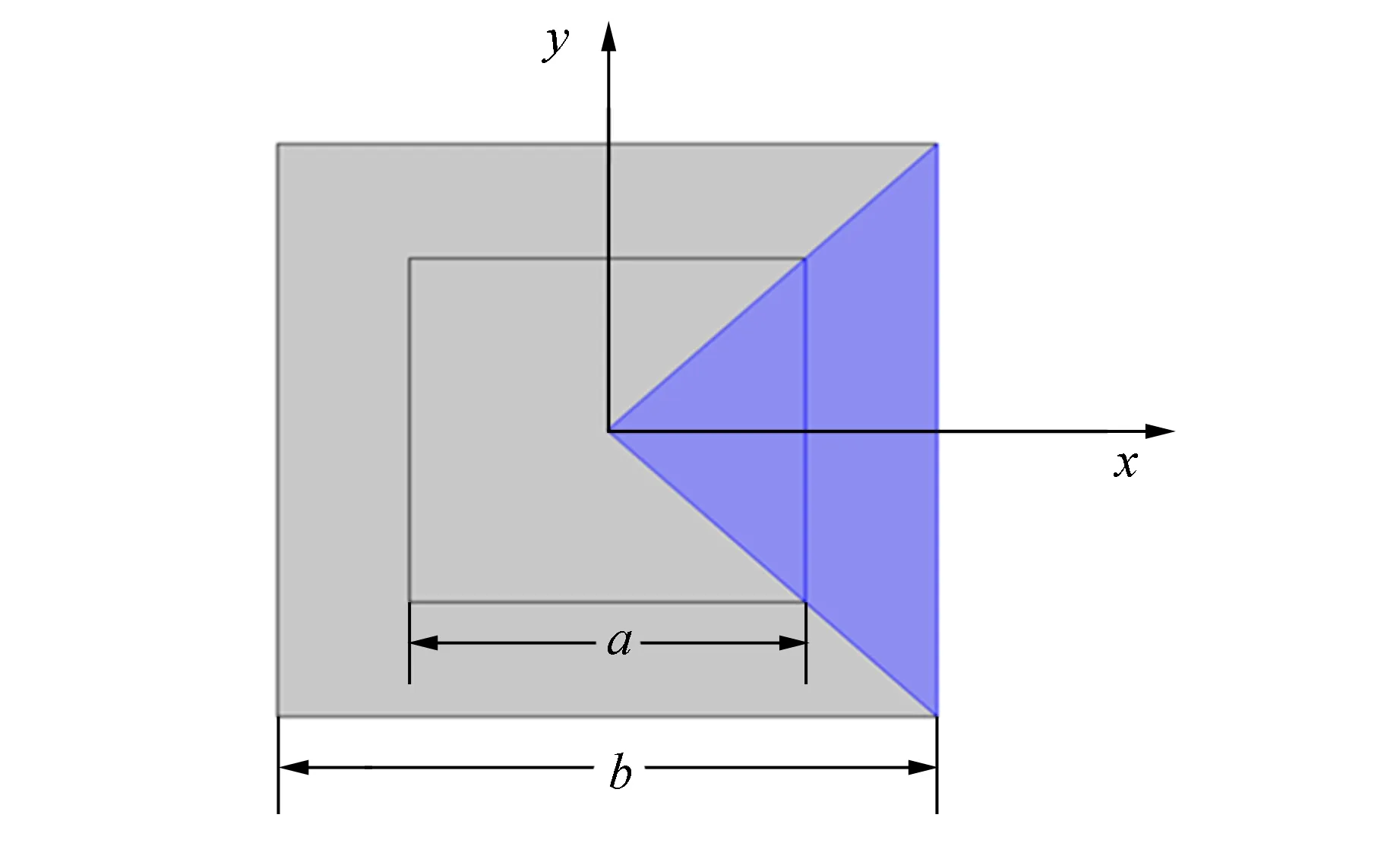
图6 正方形隐身衣空间变换示意图

进一步计算出梯形区域的相对介电常量和磁导率为

(25)

其中

对剩下的区域，构造类似的坐标变换关系，分别求出其介电常量和磁导率，得到4个梯形组合形成的方形环状变换介质的介电常量和磁导率，其张量表达式中的变量x′和y′是实际物理空间的直角坐标.模拟结果如图7所示，其中图7(a)是正方形隐身衣，正方形边长分别为a=3 μm,b=6 μm,图7(b)是通过类似方法设计的长方形隐身衣，长方形长边长是短边长的1.5倍.

(a)正方形

4 结束语

介绍了变换光学的理论，给出基于变换光学设计隐身衣的设计思路.通过空间坐标变换，推导了二维圆柱形、椭圆柱形、正方形隐身衣的变换介质在实现物理空间上的介电常量和磁导率张量公式，并通过COMSOL Multiphysics仿真软件给出了隐身仿真结果.基于变换光学的隐身衣仿真设计可作为本科生物理实验教学内容，学生可通过软件设计模拟隐身衣仿真效果.该实验有助于培养学生的创新意识，提高思考能力，有助于学生了解前沿的科学知识.