利用Mathematica改进悬丝耦合弯曲共振法测量弹性模量实验

秦月婷，张贵清，明成国

(天津科技大学 理学院 物理系，天津 300457)

悬丝耦合弯曲共振法测量弹性模量[1]，因其共振易判别，支撑的影响易排除，实验结果稳定，且有较宽的温度适用范围，而成为世界各国广泛采用的测量方法，也是我国推荐的动态法测量金属材料弹性模量的测定方法[2]，该实验项目在各高校基础物理实验中广泛开设.由于大学物理实验的教学对象是本科低年级的学生，因此在实际教学中，通常有2方面的原因使学生无法深刻理解和把握该实验原理而产生困惑，一是不清楚实验中所提及的基本概念；二是在实验理论中涉及梁的横向弯曲振动的动力学方程、微分方程求解及超越方程等复杂的数学计算.为了帮助学生更好地理解基本概念和数学计算，本文对实验中的基本概念进行了详尽阐述，将解析计算和图形演示相结合，并利用Mathematica求解微分方程数值解.在教学中降低学生学习的难度，有效地增加对该实验的实验原理的理解，同时提供了可以利用数学软件解决物理问题的直观方法和手段.

1 实验理论中的基本概念

1.1 梁的概念和分类

梁是一种承受垂直于轴线的横向载荷的杆件.将弯曲变形时的梁的轴线，即各截面形心连线取做x轴；垂直于梁的方向取做y轴.若梁在对称平面内做弯曲振动时，梁的轴线只有横向位移η(x,t)，这种模型的梁称作欧拉-伯努利梁，也称细梁;如果与梁的长度相比，横截面的尺寸并不很小，则需要考虑转动惯量和剪切形变的影响，这种梁称为铁木辛柯梁，也称粗梁[3].本实验中采用的试样为细直圆杆，为细梁.

1.2 梁的横向弯曲振动的动力学方程

对于连续介质的细梁，根据微元的受力分析，利用牛顿第二定律推导梁的横向振动的微分方程.这部分虽有些复杂，但只要清楚细梁横向弯曲时应力和应变发生的位置及其关系，即可明晰其动力学方程的来由.梁的横向弯曲振动的示意图如图1所示.图1中，虚线部分表示中性层L，半径为ρ，梁的弯曲横振动时，其线应变εx和正应力σx均为零，这意味着在中性层上根本不存在拉伸或压缩，而在中性层的两边，形变具有相反的符号；弯曲层L′，其半径为r.图2中O点称为形心，即截面图形的几何中心,z轴为中性轴.由图1可知

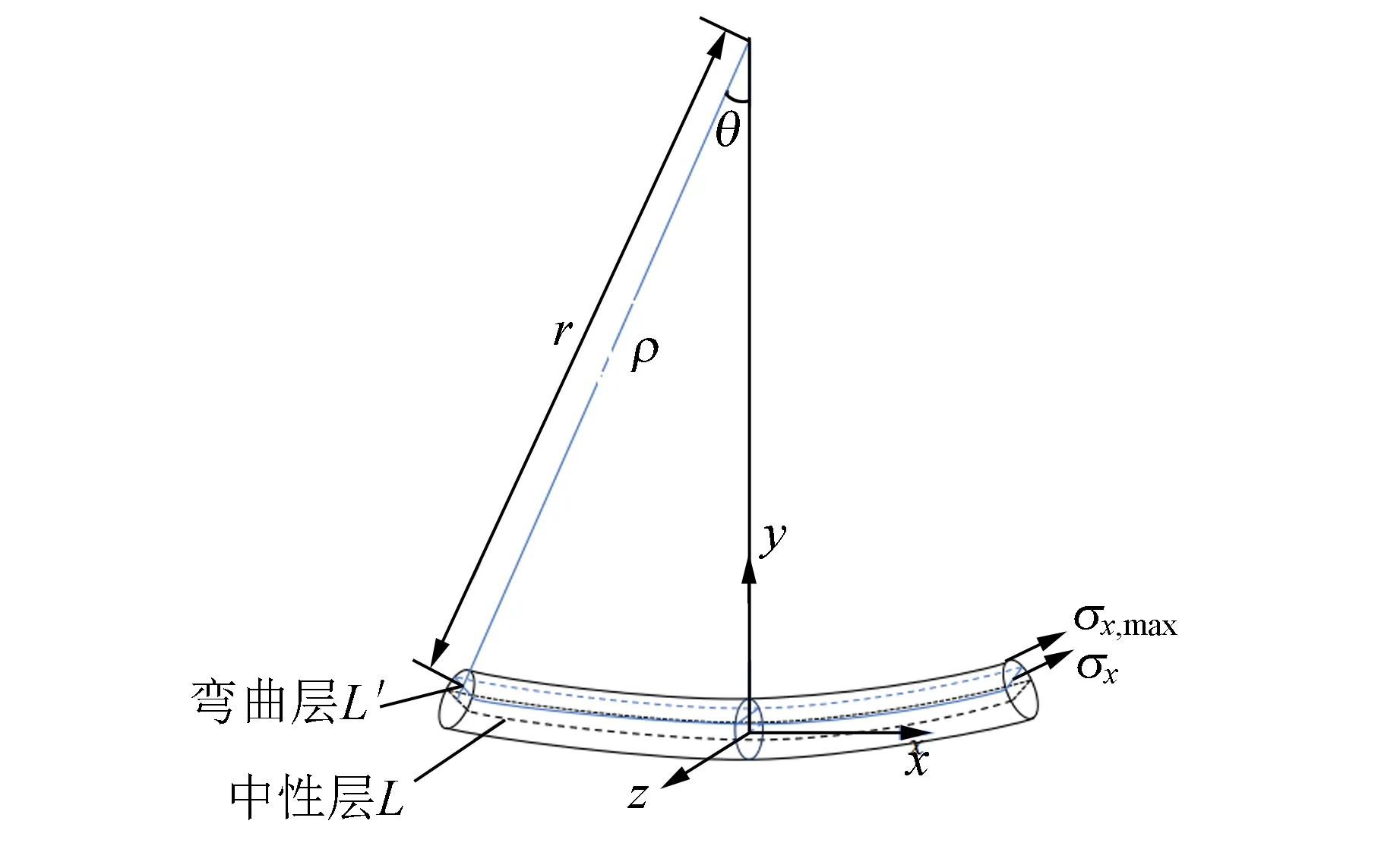
图1 梁的横向弯曲自由振动示意图

L=ρθ,L′=rθ=(ρ-y)θ,

其弯曲层的形变量δ为

δ=L′-L=-yθ,

其纵向线应变εx为

(1)

当梁的形变在弹性限度内，根据胡克定律[4]有

(2)

其中E为弹性模量，即待测物理量.

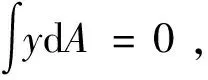
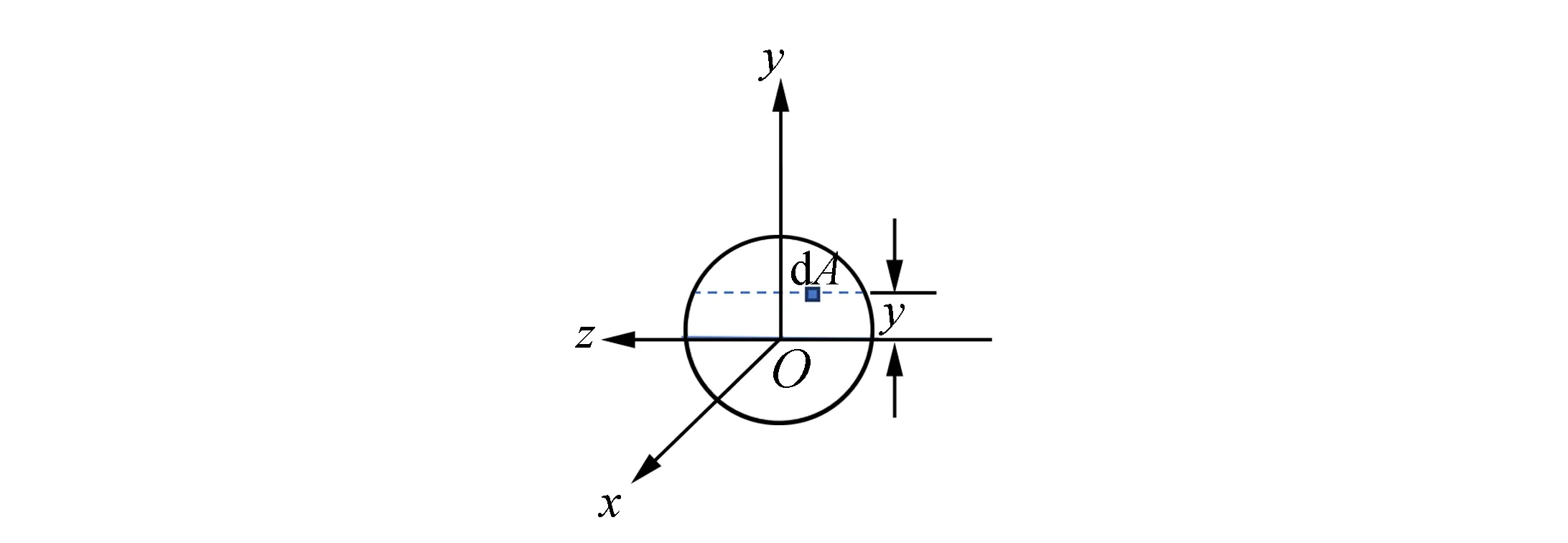
图2 图1的右视图

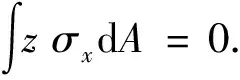
(3)

其中“-”表示与M正方向相反，M正方向为z轴正方向，M称为弯矩，表示作用在梁的给定截面上的内应力之力矩.将式(2)代入式(3)中，得

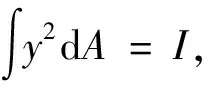
(4)

(5)

其中η称为挠度，表示中性层上一点的垂直位移(如图3所示).由式(5)可写出弹性曲线控制微分方程为[3]

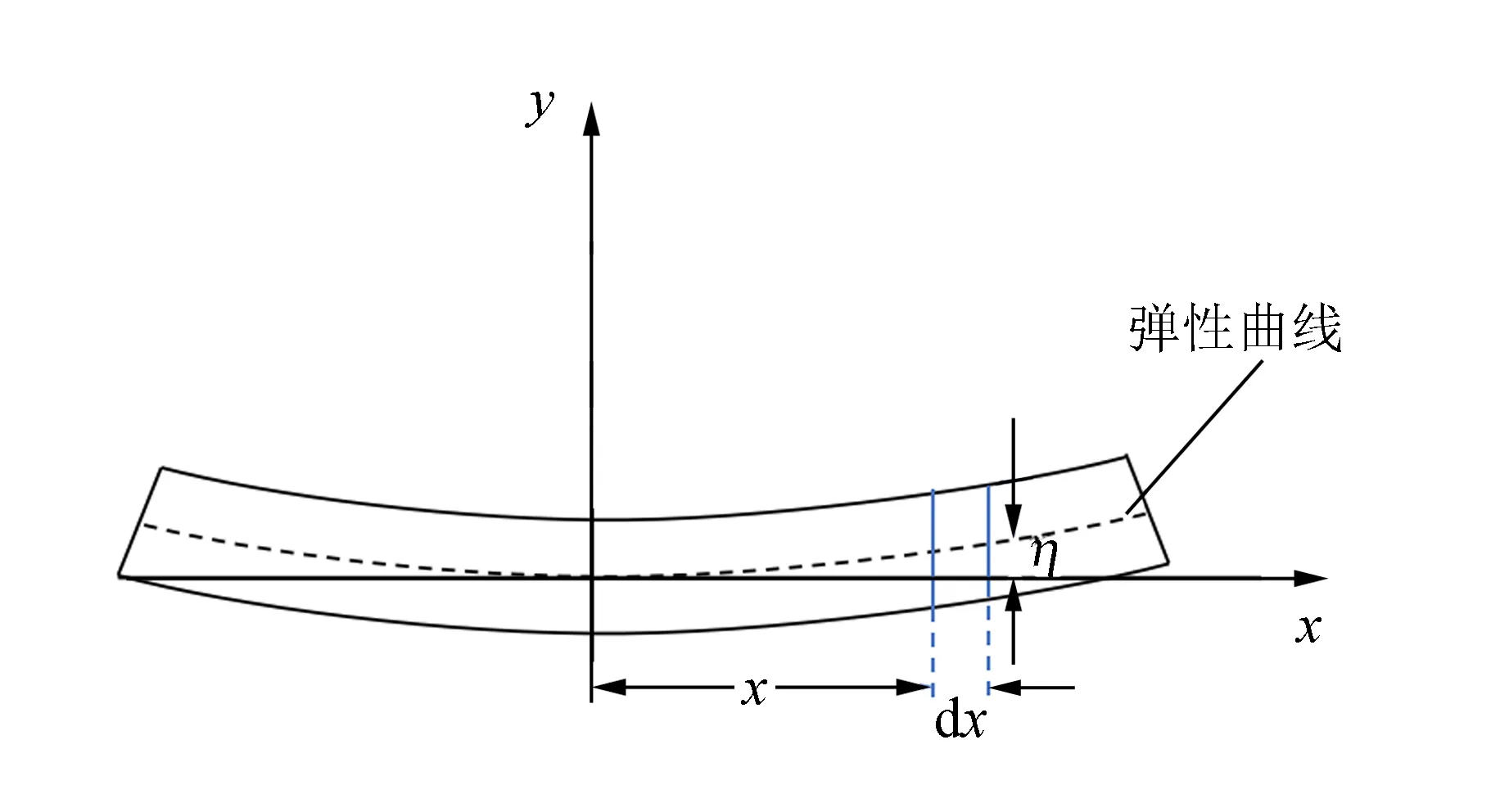
图3 图1正视图

(6)

图4中f(x,t)表示单位长度上微元所受的作用力，V为微元所受的剪切力，剪切力的定义如图5所示.因为

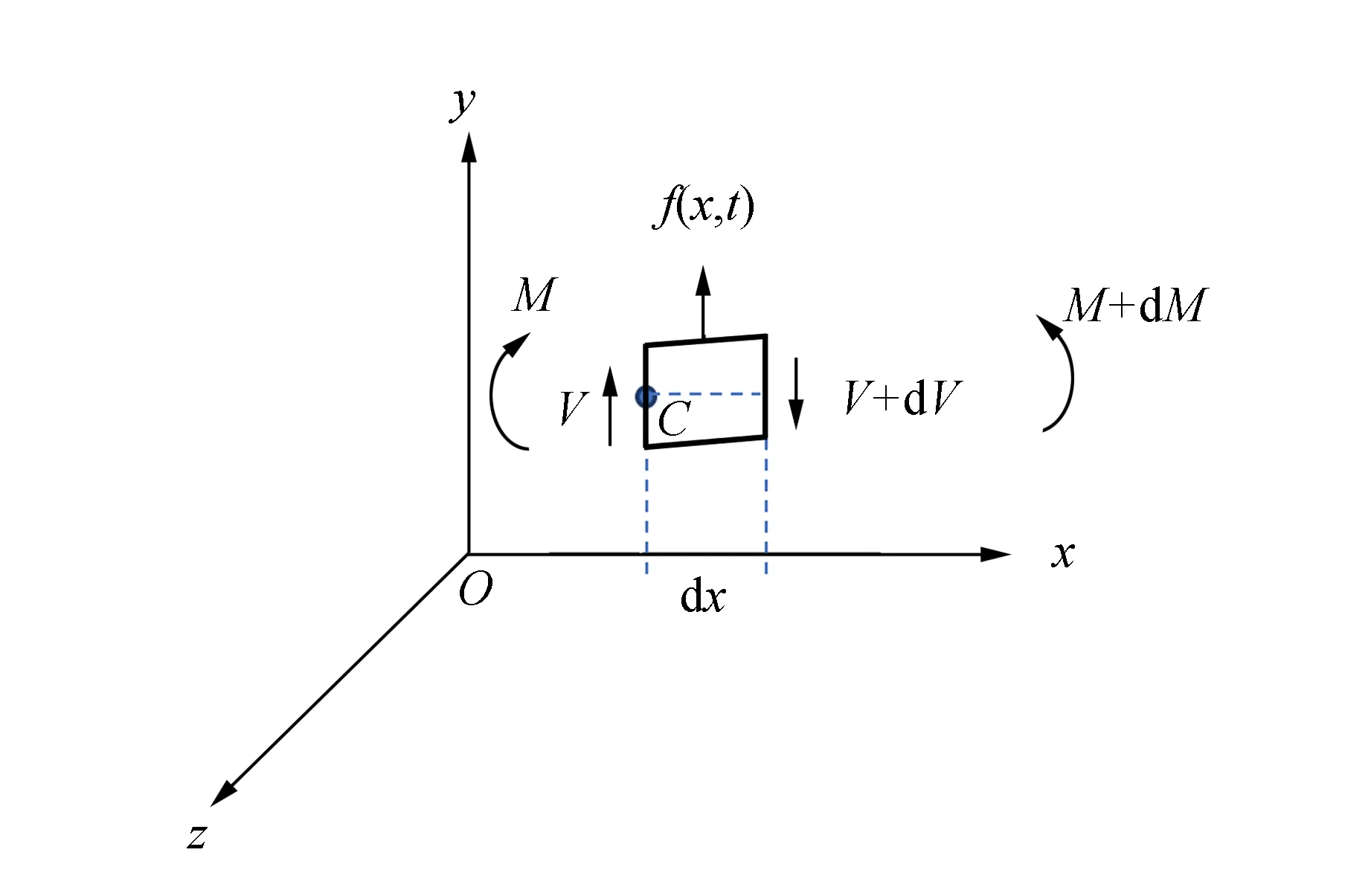
图4 微元的受力分析图

图5 微元的切应力分析图

(7)

微元中各力对过C点在轴方向上的力矩

∑Mz=0,

(8)

根据式(7)列微分方程有

(9)

其中，ρ为密度，A为梁的横截面积.根据式(8)，得

(10)

将式(10)展开后，略去高阶小项，得：

(11)

将式(11)和(6)代入式(9)中，得动力学方程：

(12)

当梁自由振动时f(x,t)=0，动力学方程为

(13)

1.3 梁的横截面惯性矩的概念

截面所在平面上关于z轴的截面惯性矩的积分为

这个概念与转动惯量类似，二者的区别仅在于用面元dA代替质量元[5].这里计算惯性矩的方法像力学中用到的垂直轴定理，即

Iz+Iy=Ix,

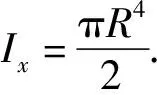
(14)

坐标轴方向如图5所示.

2 运用Mathematica求解两端自由的横向弯曲振动梁的动力学方程及相关的数值计算

2.1 运用Mathematica求解横向弯曲振动的动力学方程

把计算机辅助手段引入物理学各科教学之中，已成为提升物理教学水平的新增长点.Mathematica既能进行符号运算，又能进行数值求解，有丰富的矢量运算函数、统计运算函数、表型数据处理函数和作图函数，功能非常强大[6]，因此选用该数学软件进行数值计算.

梁的弯曲振动的动力学方程(13)中，令η(x,t)=X(x)T(t)，分离变量[2,6]得

(15)

其中，K为待定常数.由此得

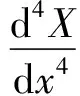
(16)

(17)

式(16)的解为梁弯曲振动的模态方程.根据式(17)，得梁的弯曲振动的固有角频率为

(18)

式(18)对处于各种边界条件下的任意形状截面的试样都成立[7-8].只要根据特定的边界条件定出常数K，代入特定截面的惯性矩I，即可得到具体条件下的频率计算公式，其中求解常数K是关键，这也是实验教学中学生理解困难的主要方面.

现在利用Mathematica 软件对(15)式进行微分方程求解和数值计算，进而得出常数K.具体计算过程及命令语句如下：

In：=ExpToTrig[DSolve[{X''''[x]-K4X[x]==0},

X[x],x]]/.Rule→Equal

Out：=X[x]==C[1]Cos[Kx]+C[2]Cosh[Kx]+C[4] Cosh[Kx]+C[3]Sin[Kx]-C[2]Sinh[Kx]+C[4]Sinh [Kx]

In：=%/.{C[1]→c1,C[2]+C[4]→c2,C[3]→c3,-C

[2]+C[4]→c4}

Out：=X[x]==c1Cos[Kx]+c2Cosh[Kx]+c3Sin[Kx]

+c4Sinh[Kx]

(19)

式(19)为式(16)的通解，也是梁弯曲振动的模态方程.

两端自由的梁悬挂在试样的节点处，则相应的边界条件为：横向作用力V为零，弯矩M为零，即

输入边界条件：

In：=MatrixForm[Flatten[{{Solve[∂{x,2}%==0]/.x→0},{Solve[∂{x,2}%==0]/.x→l},{Solve[∂{x,3}}%==0]/.x→0},{Solve[∂{x,3}%==0]/.x→l}}]]

Out：=Cos[Kl]Cosh[Kl]==1

Cos[Kl]Cosh[Kl]-1=0,

(20)

此式即为通解式(19)加入边界条件后的特解，也称为两端自由梁的频率方程.

2.2 运用Mathematica对动力学方程特解求根

利用Mathematica寻找满足式(20)的Kl值的方法.首先，利用图像法判断根的范围.

In：=Show[Plot[Cos[Kl]*Cosh[Kl]-1,{Kl,0,10}]

Out：=

由图6可知，第1个根和第2个根分别在4.7和7.8附近.依此方式，寻找到一系列满足方程(20)的根.

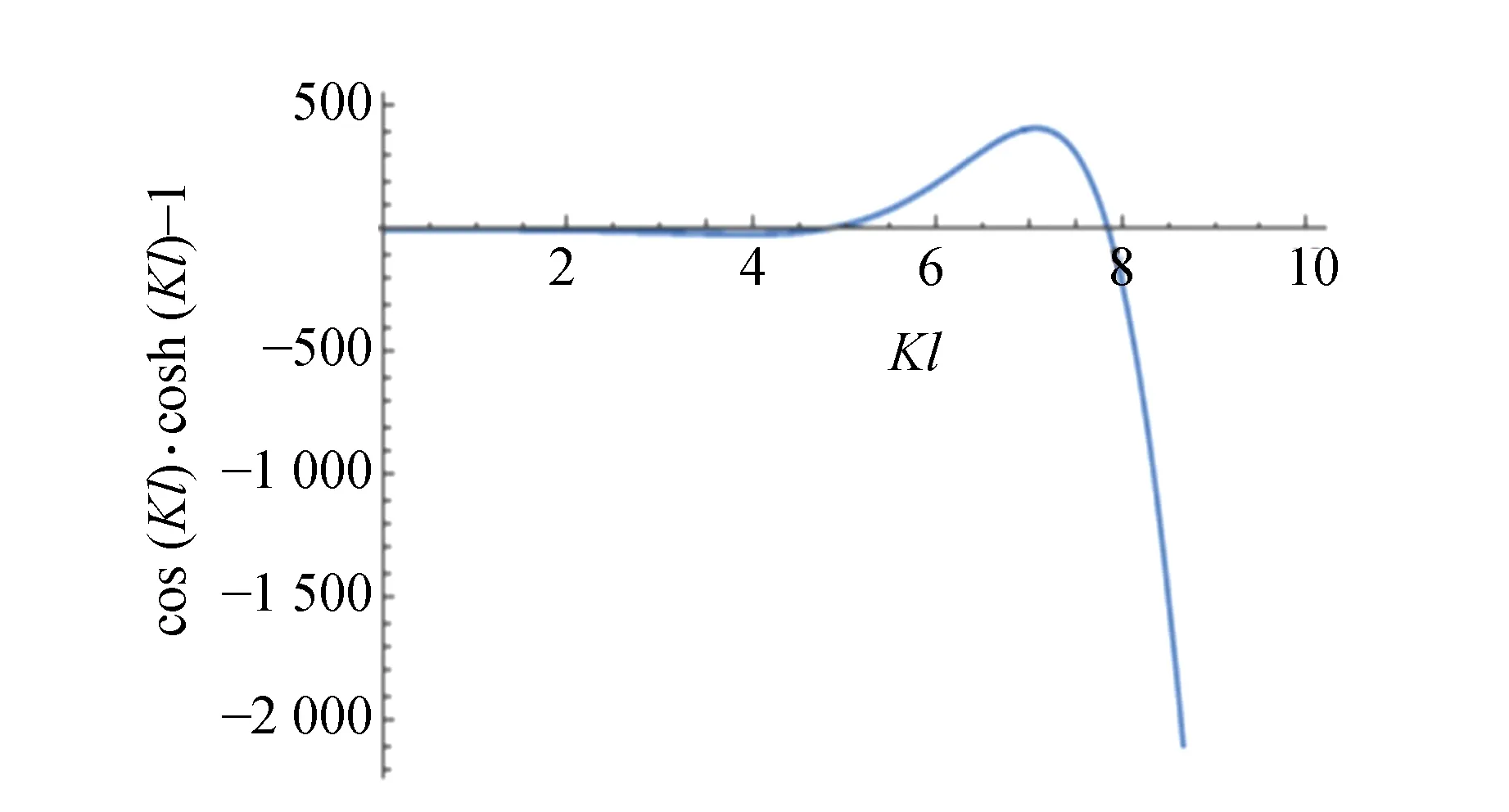
图6 cos(Kl)·cosh(Kl)-1随Kl的变化曲线

In：=FindRoot[-1+Cos[Kl]*Cosh[Kl]==

0,{x,{4.7,7.8,11.0,14.1,17.3,20.4,23.5,26.7,29.8,33.0,36.2,39.2,42.4,45.5,48.7,51.8,54.97,58.1,61.2,64.4,67.5,70.5,73.8,77.2,80.0,83.2,86.4,89.2,92.6,95.5,99.2,102.0,105.5,108.4,111.7,114.7}},WorkingPrecision→7]

Out：=Kl->{ 4.730041, 7.853205, 10.99561,

14.13717, 17.27876, 20.42035, 23.56194, 6.70354,

29.84513, 32.98672, 36.12832, 39.26991, 42.41150,

45.55309, 48.69469, 51.83628, 54.97787, 58.11946,

61.26106, 64.40265, 67.54424, 70.68583, 73.82743,

76.96902, 80.11061, 83.25221, 86.39380, 89.53539,

92.67698, 95.81858，98.96017, 102.1018, 105.2434,

108.3849, 111.5265, 114.6681}}

然后进行拟合Kl与正整数n的函数关系，并绘图(见图7).

In：=FindFit[{4.730041, 7.853205, ……,114.6681},

a+bn,{a,b},n]

Out: =Kl=1.572678+3.141516n

Kl值与正整数n之间关系的拟合方程为Kl=3.141 516n+1.572 678，拟合方程近似为

(21)

这一结论与文献[9]一致.表1给出Knl的数值解和拟合解的数值及相对偏差.

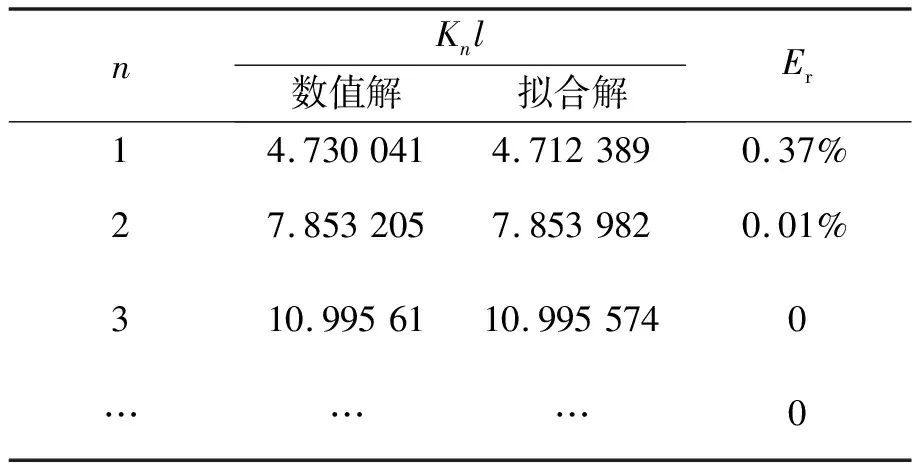
表1 Knl数值解和拟合解的数值对比表

2.3 两端自由梁的弯曲振动的角频率公式及模态函数

根据(20)式可知，两端自由的梁的弯曲振动的各阶固有角频率公式可写为

(22)

代入(14)式，得出细直圆杆的弹性模量公式为

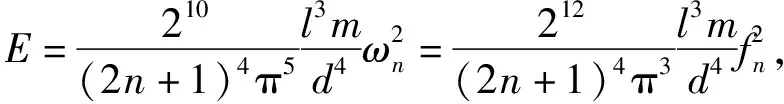
n=1，2，3…

(23)

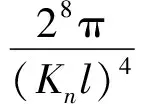
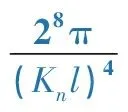
表2 数值解和拟合解下的值对比

+c4[sin(Knx)+sinh(Knx)]，n=1，2，3…

2.4 两端自由梁在基频振动时的节点位置计算和振形图

两端自由梁在基频振动K1l=4.730 041时，节点处X(x)=0，得

[sin(K1x)+sinh(K1x)]=0,

(24)

In：=Plot[-1.0178094106701914(Cos[4.730041y]+

Cosh[4.730041y])+Sin[4.730041y]+

Sinh[4.730041y],{y,0,1},Epilog→

{PointSize[Medium],Point[{{0.224,0},{0.7758,0}}]}

Out：=

由图8可知，y值在0.2和0.8附近，因此利用数值计算寻找满足式(24)的数值解为

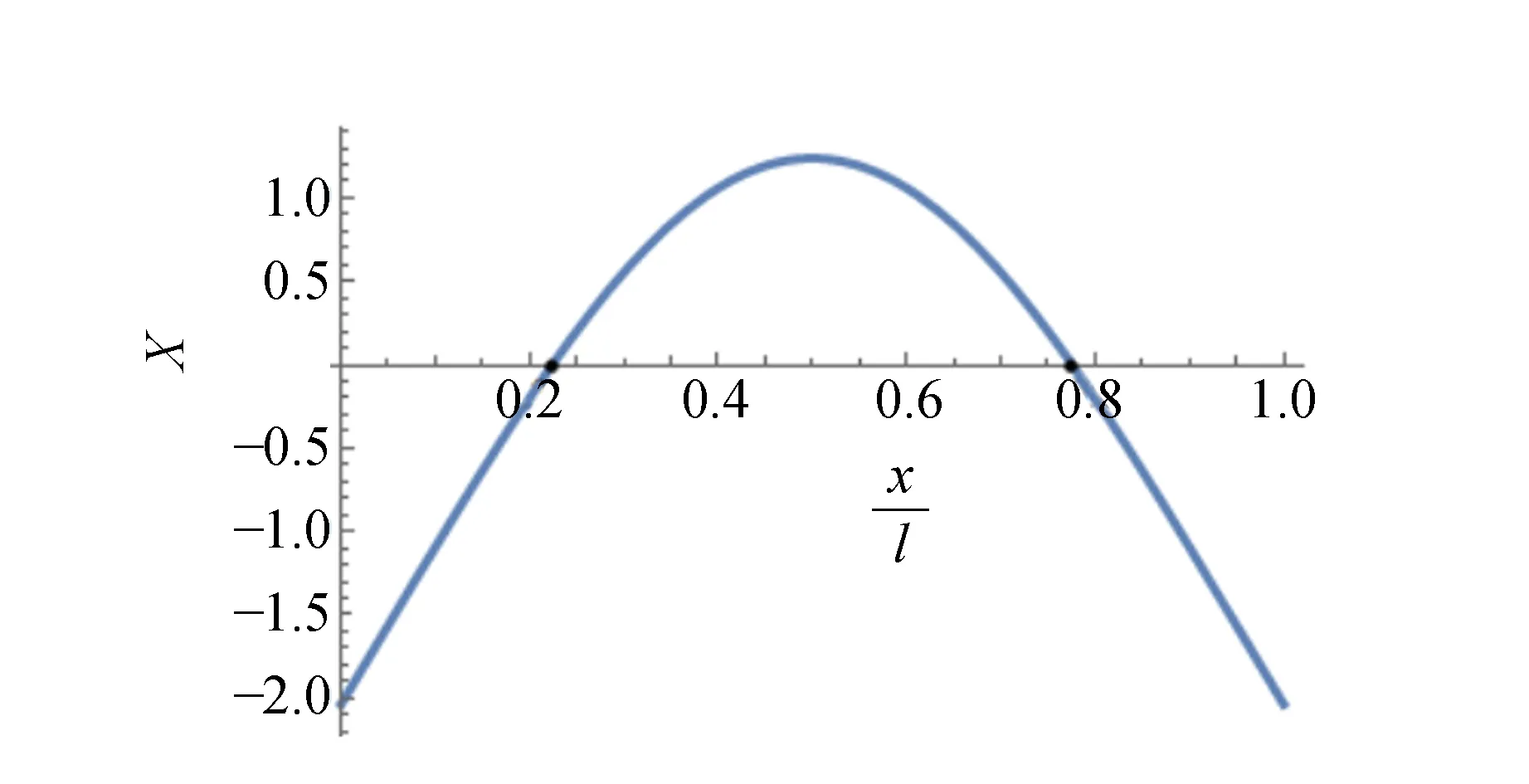
图8 当K1l=4.730 04时试样弯曲基频振动的振形图

In：=FindRoot[-1.0178094106701914(Cos[4.730041y]+

Cosh[4.730041y])+Sin[4.730041y]+

Sinh[4.730041y]==0,{y,{0.2,0.7}},

WorkingPrecision->7]

Out：={y→{0.2241575,0.7758425}}

求出y值的数值解.

当K1=4.730 041/l时，节点位置为x=0.224 137 5l和0.775 842 5l.依此方式，可计算出一系列Kl值相对应的节点位置x/l及其振形图,如图9所示.

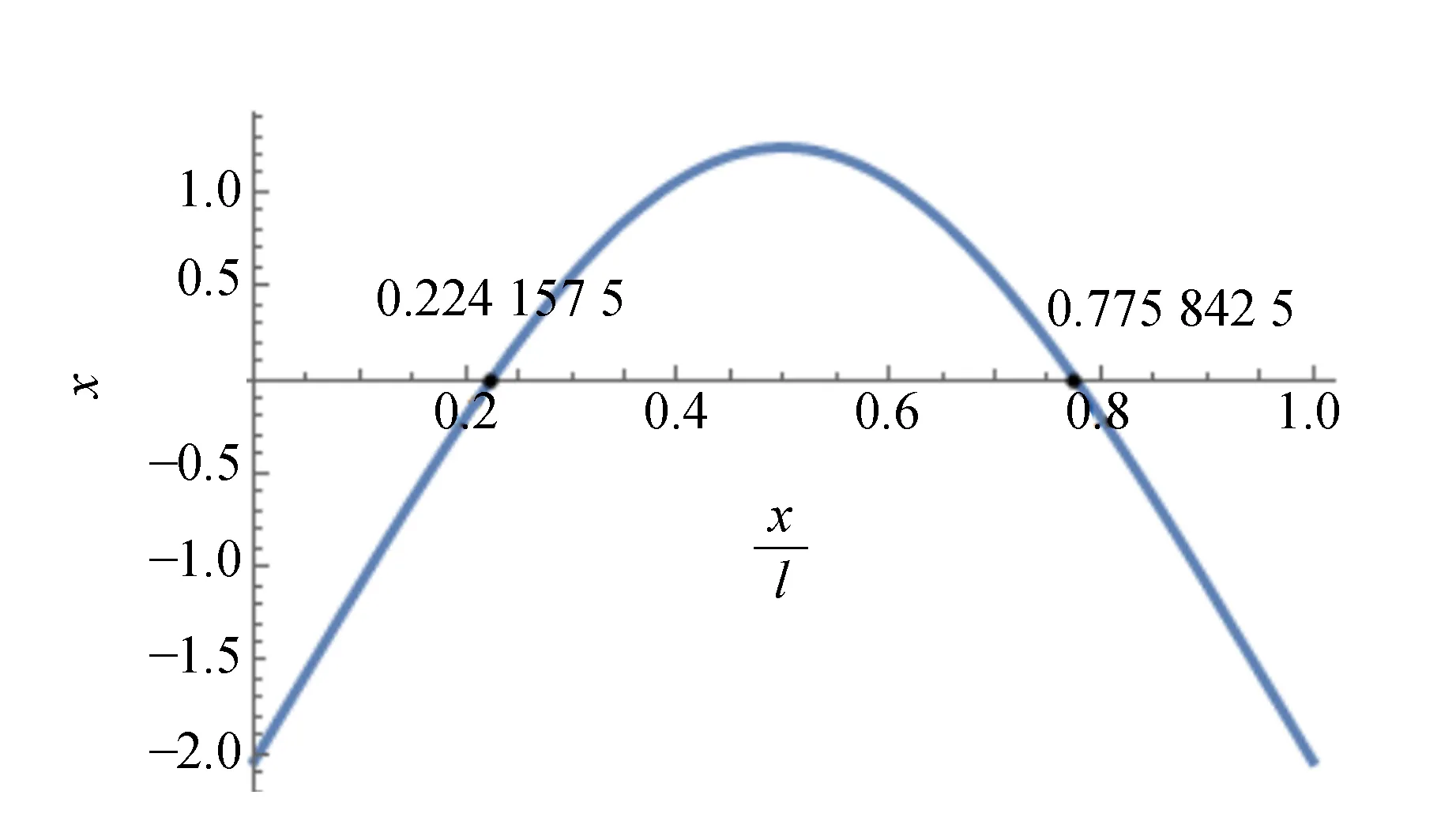
(a)Knl=4.730 041

3 结束语

综上，对悬丝耦合弯曲共振测量弹性模量的实验原理，从基本理论出发详细地推导出梁的横向弯曲振动的动力学方程.利用Mathematica对微分方程求解两端自由梁的横向弯曲振动动力学方程中频率方程的根和相应的节点位置，并拟合了节点位置及其变化规律，得出新的固有圆频率公式和模态函数；详细地给出弯曲振动的基振振形求解过程及二阶、三阶振形图.为更好地理解本实验，这部分理论内容可以在实验内容中给以补充和丰富.

在大学物理实验的教学中，面对一些较复杂的数学计算的时候，引导学生借助计算软件化解知识难点，可使物理实验原理的阐述更加明晰，物理概念得到深化，同时拓宽了物理实验课程的内容，也促使物理实验课程的进一步改进和拓展.对于学生而言，学懂弄通是提高学生学习兴趣的关键，引入计算恰恰是使学生对实验原理理解更加透彻的一种有效途径，且培养了学生利用现代化手段解决问题的能力.因此，这种教学模式的改进在进一步提升物理实验课程的学术水平和教学水平，提升学生学习的兴趣方面，起到了极大地促进作用.