排列组合解题策略研究

李昌成

(新疆乌鲁木齐市第八中学 830002)

在解决排列组合问题过程中，常出现的问题是：解完题后自我感觉良好，但答案却是错的.这是因为此类问题比较抽象，不知从何下手；题型较多，不知用何方法；易重复，常遗漏，却不知重漏于何处.排列组合各类型题的解题方法几乎不通用，很有必要归类总结，形成技能.下面依托部分高考题介绍一些常见的策略.

一、特殊元素优先

例1 从6人中选4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览，要求每个城市有一个人游览，每人只游览一个城市，且这6人中甲、乙两人不去巴黎游览，则不同的选择方案共有( ).

A.300种 B.240种 C.144种 D.96种

评注使用这个策略务必选准特殊元素，并对其利用两大计数原理合理处理，否则，易导致重复或遗漏.

二、特殊位置优先

例2 在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，不能被5整除的数共有____个.

评注特殊位置是需要一定背景才能产生的，解题时需要对题意准确把握，找准特殊位置，否则易导致重复或遗漏.

三、准确分类

例3 不共面的四个点到平面α的距离都相等，这样的平面α共有( ).

A.3个 B.4个 C.6个 D.7个

解析满足条件的平面分为两类，第一类是三棱锥的高的中垂面，有4个；第二类是三棱锥对棱的公垂线段的中垂面，有3个.故共有7个，选D.

评注类似本题的立体几何问题难以找准分类的标准，并且分类标准受空间位置关系影响较大，特别容易遗漏，务必谨慎思考.

四、恰当分步

例4 安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有( ).

A．12种 B．18种 C．24种 D．36种

评注这类题容易这样错误操作：先安排一项工作给某人，再给每人安排一项工作.这个分步不恰当，某人两次接受工作，不合情理,必重复.

五、先选后排

例5 若从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同工作，则选派方案共有( ).

A.180种 B.360种 C.15种 D.30种

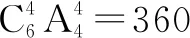
六、正难则反

例6 在100件产品中有6件次品,现从中任取3件产品，至少有1件次品的不同取法的种数是( ).

A. 26226 B.29106 C.27656 D. 836156

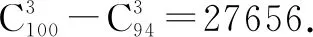
评注当问题的正面情形较多，反面情形较少时，最好从反面解答，本解法又称排除法.

七、相邻捆绑不相邻插空

例7 用1,2,3,4,5,6,7,8组成没有重复数字的八位数，要求1与2相邻,3与4相邻,5与6相邻，而7与8不相邻，这样的八位数共有____个.(用数字做答)

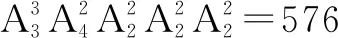
评注当已知中有相邻的条件或相邻的含义时，需用捆绑策略，先处理捆绑后的整体，再处理被捆绑的元素；当已知中有不相邻的条件或不相邻的含义时，需用插空的策略，先把其他元素排好，再将这些元素插入.解题中贯穿分步计数的乘法原理.

八、转行拉直

例8公交车上现有最后两排的6个位置，刚好有6名中学生来乘车，他们有____种坐法.

评注这种题出现了干扰条件，理论上与排数，位置无关，直接视为一排，各位置一样对待.

九、定序分类

例9 某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目.如果将这两个节目插入原节目单中，那么不同插法的种数为( ).

A.42 B.30 C.20 D.12

十、圆排列分类

例10 4人围坐在一张圆桌上就餐，共有____种坐法.

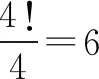
十一、平均分组分类

例11 四支球队，两强两弱，现把他们平均分成两组，共有____分法.

评注这类问题属于平均分组，处理它的一般方法是：先按要求分组，再除以组数的阶乘.对于部分平均分组的，第一步不变，第二步的组数为参与平均分组的组数，而不是全部组数.

十二、构造模型

例12 体育老师让学生把10个篮球分装到6个篮球筐内，要求每筐不空，共有____种分装方法.

评注这种方法又称隔板法.使用时要注意是否允许隔板相邻，这对问题影响较大.在实际问题中，抽象出这种模型是关键，如下面一个例题.

例13已知集合A={a1,a2，…，a50}与集合B={b1,b2，…，b50}，则能建立多少个映射f：A→B，使得B中每个元素都有象，且满足f(a1)≥f(a2)≥…≥f(a50).

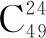
十三、对称分类

例14 如图1，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可以选择，则不同的着色方法有____种.(以数字作答)

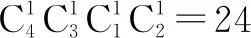
评注对于区域1而言，2与4，3与5均属于“对称”位置，因为前者对后者计数有制约性影响，所以务必分类研究.事实上，这种对称位置有时也较隐蔽，需要抽象处理.

十四、定向分配

例15 现有3名医生和6名护士被分配到3所学校去开展体检工作，每校分配1名医生和2名护士，共有____种分配方法.

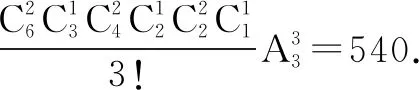
十五、依次插入

例16 在一次文艺演出中，有3小品，2个歌舞和1个独唱等节目，要求同类节目不排在一起，共有____种排法.

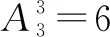
所以同类节目不相邻的排法种数是48+72=120种.

评注本题在第二步中极易出错，笼统地将三个节目插入，表象上满足了条件，实际上有很多同类节目相邻的情形.务必依次插入，步步为营.

排列组合问题多数都是应用题,多以选择或填空形式出现,小巧灵活,有很强的独立性、抽象性和综合性；同时对分类讨论、数形结合、等价转化等数学思想有着较高要求,学生不易掌握,为历年高考常考内容.因此以上思维方法和解题策略十分重要.同时灵活应用两个原理:分类问题用加法,完成一件事的几类方法之间是独立的,计数时不重不漏；分步问题用乘法,完成一件事的几步之间是连续的,计数时缺一不可.触类弄通，各个击破，高考时，我们就胸有成竹了.