不规则波激励下磁力双稳态波浪能转换装置的能量捕获特性研究

席 儒，张海成，陆 晔，徐道临，吴 博

(1. 湖南大学 机械与运载工程学院，湖南 长沙 410082； 2. 中国船舶科学研究中心，江苏 无锡 214082； 3. 湖南海浮科技有限公司，湖南 长沙 410082)

在数次工业革命的推动下，人类的生产力得到显著提升的同时，对能源的需求量也在近百年来急剧增加。传统的不可再生的化石能源如煤、石油、天然气等在短时间内被过度使用，引发了一系列的环境问题如温室效应、酸雨、雾霾等[1-2]，严重威胁了人类的健康与生存。寻求可再生的清洁能源作为化石能源的替代品成为了近年来热门的研究课题。

海洋中蕴含丰富的能源，波浪能作为其中的一种形式，具有可再生、无污染、储量巨大等特点，受到了许多能源领域研究学者的关注[3]。自波浪能利用被提出以来，已提出了大量的波浪能转换装置，如振荡水柱式、点吸收式、越浪式、摆式、筏式、点头鸭式等[4-6]。其中点吸收式波浪能转换装置由于其具有结构简单、易于安装维护和可靠性较好等优点，得到了学者和工程人员的广泛关注。由振动理论可知，线性点吸收式波浪能转换装置在波浪激励下处于共振状态时运动幅值最大，此时的波能捕获效率最高。然而线性装置的有效波能捕获频带非常窄，即当波浪激励频率稍微偏离装置固有频率时，运动幅值明显降低，导致波能捕获效率锐减。而海洋中的波浪频率时刻都在变化，呈现随机波谱的特征，因此线性装置在实际海域中的应用因其效率低下存在较大的局限性。

为了提高波能转换装置的效率，有学者提出采用主动控制的方法，如相位控制[7]、滑模控制[8]和短期波浪预测模型控制[9]等。相关研究表明，控制方法可以有效的提高波能捕获效率，但前提是控制装置需要提前尽可能详细地预测和分析入射波的波况，一旦控制装置在分析过程中出现误差，波能转换效率将可能急剧降低[10]。其次控制装置在执行过程中需消耗额外的能量、复杂的执行机构增加安装和维护成本，这些都制约了控制方法的应用。

不同于主动控制技术，利用被动的非线性捕获机制来提高能量转换效率成为近年来的研究热点，其中双稳态机制作为一种典型的非线性机构已应用在不同的能量捕获系统中。在波浪能捕获系统中，已有一些学者开展了研究。Zhang等[11]首次将对称斜弹簧双稳态机构引入到波浪能转换装置中用以提高波能捕获效率，结果表明该装置可以有效提高低频范围内的波能捕获效率。采用气弹簧，TodalShaug等[12]提出了一种“WaveSpring”负刚度机构应用于点吸收式波能捕获装置中。实验研究结果表明，在不规则波激励下，安装该机构的波能转换装置的捕获效率是线性系统的近3倍。除此之外，也有学者提出了磁弹簧[13]、多连杆[14]等不同类型的双稳态机构用于点吸收式波能转换装置。

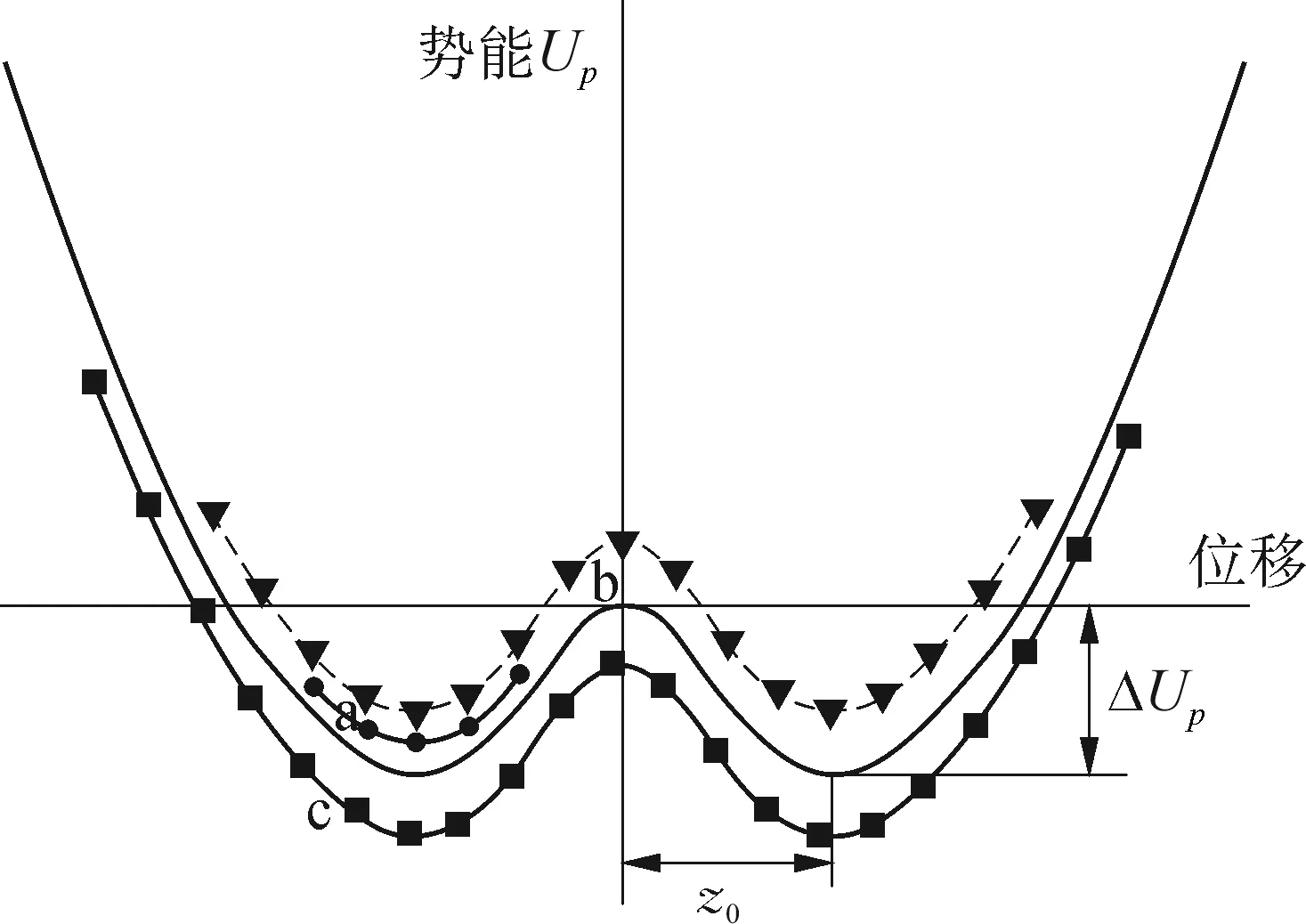
图1 双稳态势能曲线示意

双稳态机构的势能曲线如图1所示，由于系统存在两个稳定平衡点和一个不稳定平衡点，故系统存在三种可能的运动形式：1) 单 阱小幅运动；2) 阱间复杂运动；3) 双阱大幅运动。双阱大幅运动即为所寻求的能量转换的目标运动状态，此时波浪能转换装置的捕获效率最佳。而决定双稳态系统的运动形式最重要的参数即为图1所示的势垒高度ΔUp和稳定平衡点间距z0。只有当系统外激励大于一定值时，才能越过势垒进行双阱大幅运动，此时双阱间大幅运动的幅值又由稳定平衡点的间距决定，即大的平衡点间距对应大的运动响应幅值，因此为了适应不同的外部激励条件，需要双稳态机构存在较宽的阱间距离同时势垒高度较小。然而对于传统双稳态装置来讲，通过调整机构参数只能达到单方面的效果，并不能同时降低势垒高度和拓宽平衡点间距。所以在小幅波浪激励条件下，双稳态波能转换器的效率显著降低，甚至低于等效线性系统的效率。

文中提出了一种新型磁力双稳态波能转换装置，通过在一对同向充磁的负刚度磁环基础上附加一对异向充磁非线性正刚度磁环，选取合适的结构参数，可达到降低势垒高度和拓宽平衡点间距的效果，提高点吸收式波浪能转换装置的捕获效率，拓宽装置应用频带，特别是改善在小幅波浪激励条件下的捕获效率。

1 动力学模型

为简化起见，这里研究仅考虑浮子式点吸收波能转换装置的垂荡自由度运动。点吸收式磁力双稳态波浪能转换装置简图如图2所示，主要由半径为R的浮球、连杆、磁力双稳态机构、电动机和支撑架组成。xoz笛卡尔坐标系的坐标原点与浮球的球心重合，其中x轴与浮球静平衡时的水面重合，z轴竖直向上。

图2 点吸收式磁力双稳态波浪能转换装置示意

图3 新型磁力双稳态机构

1.1 磁力双稳态机构

如图3所示，磁力双稳态机构主要由一对同向充磁的负刚度磁环和一对异向充磁的正刚度磁环组成。参数r表示内部磁环的内径，δ表示磁环的磁隙宽度，l表示内外磁环的厚度，h和h0分别表示负刚度磁环和正刚度磁环的高度。考虑垂荡方向的自由度，磁环间的轴向作用力函数Fm表达式如下[15]

(1)

(2)

式中：σ=J·n表示磁极表面密度，J和n分别表示磁极化向量和磁体表面单元法向量，μ表示磁导率，Rm=r+l+δ/2表示内部和外部永磁环的平均半径。

1.2 动力学方程

基于Cummins方程[16]，建立系统时域动力学方程如下

(3)

式中：m和A∞分别表示浮子的质量和其在无穷大频率处的附加质量。由浮子静力平衡可知m=2ρπR3/3，其中ρ为海水密度。对于仅考虑垂荡自由度的浮子可知A∞=0.5 m[17]。其中静水恢复力Fr=-ksz(t)，对于在垂荡位移较小的条件下可知静水恢复刚度满足ks=ρgπR2，g为重力加速度。

系统的控制方程中的卷积积分项表示波浪的辐射力，表征了流体的记忆效应。其中脉冲响应函数hz(t)可以通过浮子的辐射阻尼系数Bz(ω)求出

(4)

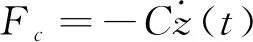
动力学方程等号右边fir(t)表示不规则波激励下的波浪激励力。

1.3 不规则波模型

在波浪研究中，通常采用不规则波模型来模拟复杂随机的真实海浪。在满足波浪谱的分布规则前提下，使用无限多个不同的规则波叠加来实现不规则波模型的效果。文中计算所采用的波浪谱为Jonswap谱[18]，其谱密度表达式如下

(5)

式中：Hs表示有效波高，ωp表示谱峰频率，Tp=2π/ωp表示谱峰周期。谱峰因子γ设定为3.3，当激励频率低于谱峰频率即ω≤ωp，谱峰形状参数χ设定为0.07，大于激励频率时χ为0.09。菲利普参数αJ表达式如下

(6)

为了通过叠加法获得不规则波的时间序列，首先需要将Jonswap谱离散成无限个不同振幅不同频率的规则波。第i个规则波成分的频率ωi可以表示如下

ωi=ω0+i·Δω

(7)

式中：ω0表示计算最低频率，Δω表示频率间隔。

第i个规则波成分的幅值Aωi可以通过如下表达式计算

(8)

浮体所受到的不规则波作用力fir(t)可以采用无限个不同频率和不同随机相位的规则波成分叠加来表示

(9)

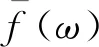
(10)

为了开展数值仿真分析，同时考虑波浪的有效频段，选取了N个规则波成分来近似模拟上述的无限个规则波成分叠加的效果。数值计算中设定N=40，最低初始频率为ω0=0.04 rad/s，频率间隔为Δω=0.04 rad/s。

1.4 状态空间模型

直接计算系统的动力学方程将会由于其中存在的卷积积分项导致运算量非常大，给数值分析带来不便。而根据Taghipour的研究发现[19]，使用状态空间模型方法替代处理卷积积分项将比直接计算后者提高了将近8倍的计算速度。

对于一个动力学系统，其激励u(t)与响应y(t)之间的关系可以用以下三种方式来表示

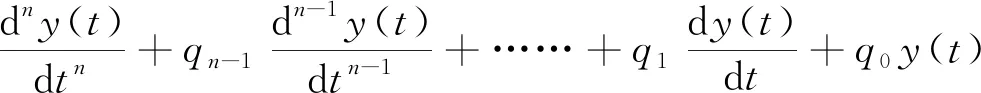
(11)

(12)

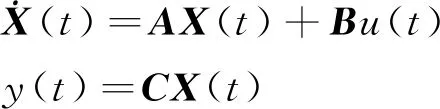
(13)

第一种为带高阶导数的常微分方程(11)，第二种为卷积积分方程(12)，第三种状态空间模型表达式(13)。以上三种方式对时域内的动力学系统进行了等价描述[19]。

对比方程(11)与方程(12)，可得

hz(t)=CeAtB

(14)

对比方程(13)与方程(14)，可得

(15)

(16)

(17)

对方程(11)进行拉普拉斯变换可得

(18)

考虑传递函数H(s)，并对脉冲响应函数hz(t)进行傅里叶变换可得

(19)

式中：j为虚数单位。对于动力学方程(3)而言，垂荡速度与脉冲响应函数是该动力学系统的输入，因此利用状态空间模型方法近似替代卷积积分项后的表达式如下

(20)

为了确定系数A,B,C，参考了Taghipour所提出的方法[19]，即基于浮子的水动力系数，采用频域识别方法。通过傅里叶变换，可以将脉冲响应函数hz(t)写成频域内浮子的附加质量Az(ω)和辐射阻尼Bz(ω)的函数，表达式如下

(21)

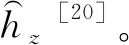
(22)

式中：s=jω，且系数θ=[pn-1,pn-2,……,p1,qn-1,qn-2,……,q0]可以通过使用最小二乘法求解获得，再根据表达式即可确定系数A,B,C。

1.5 波浪能捕获宽度

计算求解动力学方程(3)后即可获得系统的动力学响应，波浪能捕获装置单位时间内捕获的波浪能Er可表示为

(23)

其中，T0表示时间间隔。根据线性波浪理论[16]，对于规则波而言，单位宽度入射波波前单位长度的入射波浪能可表示为

(24)

对于不规则波，利用谱分析法可得其入射波浪能为

(25)

在波浪能转换特性研究过程中，捕获宽度常被作为评价波浪能转换装置转换效率的参考值，它表示波浪能转换装置吸收能量与入射波波浪能的比值[21]。表达式如下

(26)

1.6 势能函数

设动力学方程(3)中的静水恢复力Fr和磁力Fm的合力为Frz=-Fr-Fm，则系统在垂荡方向上的势能函数Up表达式如下

(27)

其中，函数ψ为式(2)中函数φ的原函数。函数ψ的表达式如下

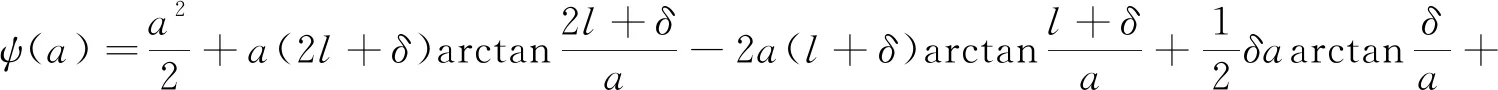
(28)

2 数值计算结果分析

在分析过程中，选取了R,ρ,g作为特征量对各参数进行无量纲化处理

其中，选取计算的模型参数为R=5 m,ρ=1 025 kg/m3,g=9.81 m/s2。结合Zhang等[22]的研究工作，发现磁环参数中相比于内磁环内径r*、磁环厚度l*以及磁隙宽度δ*，磁环高度h*对轴向磁力影响最大。因此在其研究基础上选取计算的磁力双稳态机构结构参数如表1所示。

表1 双稳态机构磁环参数表

在利用状态空间模型实现浮球辐射力卷积替代过程中，采用了四阶的状态空间模型近似替代，如图4所示，可知替代结果与文献近似解析方法求解的水动力系数结果二者拟合效果良好，验证了状态空间模型的可靠性。

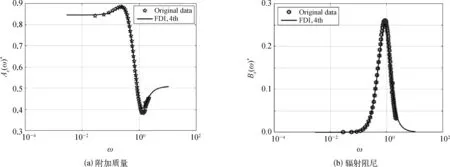
图4 浮球水动力系数的卷积替代结果验证

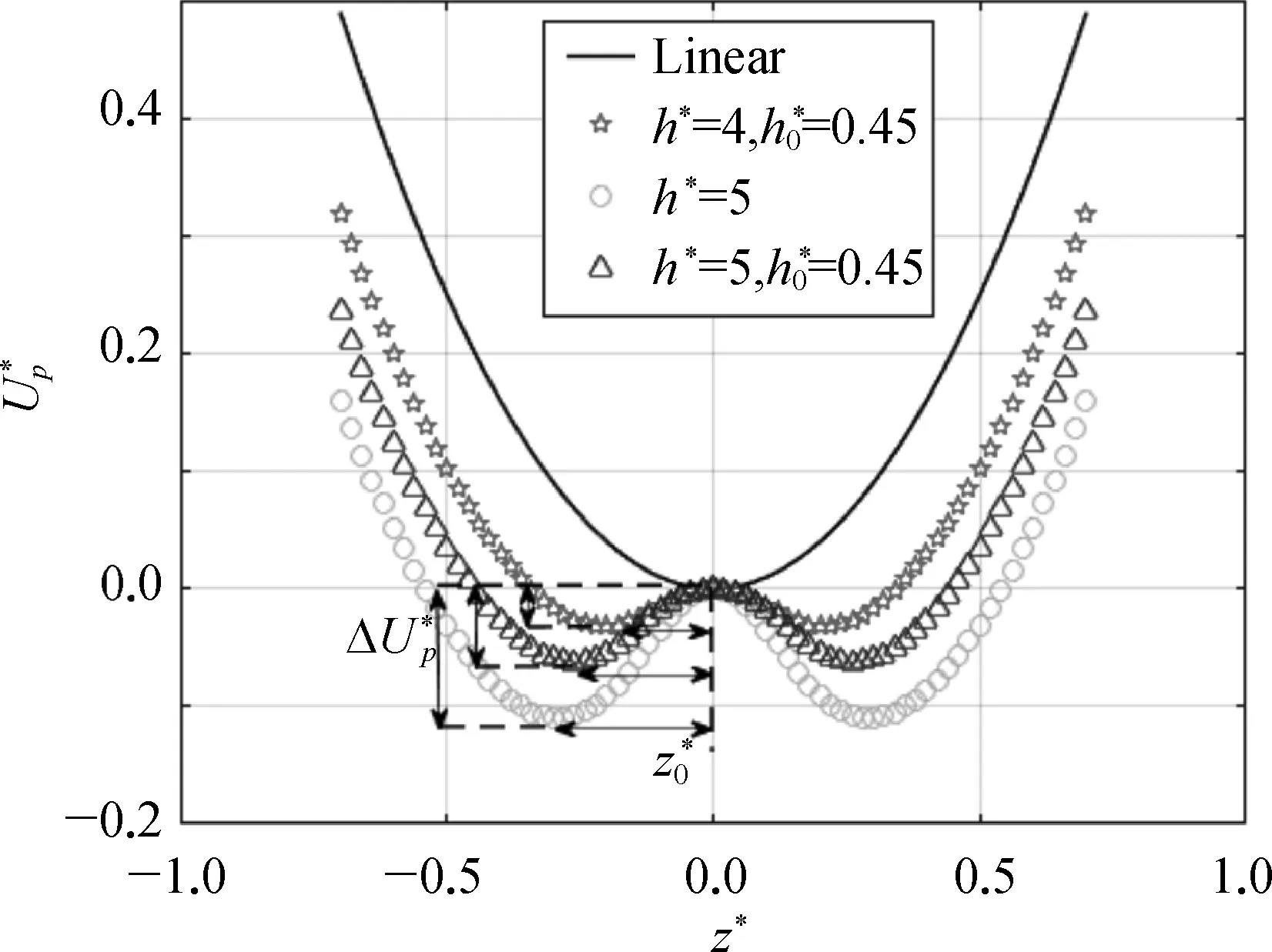
图5 不同结构参数下磁力双稳态装置的势能曲线变化

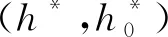
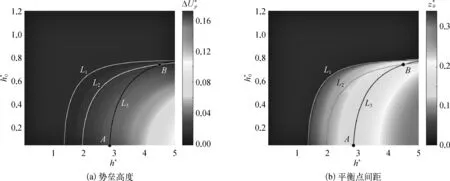
图6 双稳态机构势垒高度与稳定平衡点间距随结构参数变化云图

图7 不同装置的捕获宽度随阻尼系数变化曲线和势能曲线

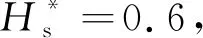
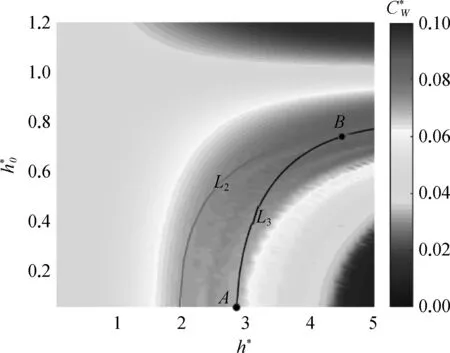
图8 捕获宽度随结构参数变化云图

图9 捕获宽度随不同波浪和结构参数的变化曲线

图10 三种不同装置捕获宽度随波况参数变化云图

3 结 语

提出了一种可用于波浪能转换装置的新型磁力双稳态机构，该机构主要由两对不同充磁方向的磁环串联组成，可通过调整磁环参数来实现改变系统双稳态特征的效果。数值分析中采用Jonswap波浪谱来模拟真实海域下的不规则波，分析了不同不规则波激励下波浪能转换装置的波能捕获效率随结构参数的变化规律。结果表明，相比于线性波能转换装置，新型的磁力双稳态装置能有效提高波能转换效率，拓宽转换频带，尤其可显著提高在小幅波浪激励下的波能效率。本研究对于波浪能的工程应用具有重要的理论借鉴意义。