新型直立式透空堤消浪性能数值研究

杜沛霖，孙昭晨，梁书秀

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

随着港口工程向生态、环保的理念转变，传统防波堤水体交换能力差、掩护区域内泥沙淤积和水质污染等问题日益凸显，逐渐不能适应工程建设的诸多要求。透空式防波堤具有良好的水体交换能力，有利于维持港内水质，缓解涨落潮时口门流速较大的问题。另外，透空结构能够减轻波浪反射，减小波浪力对堤身稳定的不利影响，因此具有良好的应用前景。

对于透空式防波堤，前人已提出了多种不同的结构形式，并做了大量的理论分析、模型试验和数值模拟的工作[1-3]。Isaacson等[4]分析了开孔率、结构尺寸、波长等参数对开孔透空堤的消浪性能的影响。Twu等[5]研究了直立式透空堤对斜向来浪的衰减作用，分析了波浪入射角对透射系数、反射系数和波能损失的影响。Liu等[6]研究了双层水平板在线性波作用下的水动力特性，探讨了板的淹没深度、厚度和间距的影响，并指出水平板布置在自由水面附近时的消浪效果更好。李玉成等[7]对梳式沉箱透空堤进行了模型试验，得出其可以在减小波浪反射的同时能减小结构受力的结论，并给出了波浪力折减系数及波浪反射系数与各参数间的经验公式。潘春昌等[8]对透空式圆弧板防波堤进行了模型试验，分析了圆弧板的间距及层数对消浪性能的影响，并指出圆弧板结构的消浪效果优于水平板结构。

近年来，能够模拟波浪生成和传播的数值水槽取得了较大发展。俞聿修等[9]采用波浪叠加法和线性过滤法，对多向不规则波进行了数值模拟。王永学[10]采用线性造波机理论，通过给出可吸收数值造波的边界条件，建立了无反射数值波浪水槽。数值方法在研究波浪与结构物相互作用的问题中也得到广泛的应用。岳景云等[11]通过复合边界元法模拟了线性波与外壁透空双方形沉箱的相互作用，分析了方箱所受无因次波浪力及周围绕射系数的分布。李昌良等[12]通过VOF方法对水平斜插板式透空防波堤的消波性能进行了研究。李凌等[13]通过在动量方程中附加源项，采用黏性流数值造波和消波的方法，模拟了波浪与两个垂直刚性薄板的相互作用。杨甜丽[14]采用仿物理推板的方法，通过固壁边界震动产生波浪，研究了半圆体防波堤的水动力特性。

目前，对于带有透浪通道的直立式防波堤，以往的文献中研究相对较少，且缺少对此种防波堤消浪性能和透空率之间关系的研究。因此，在目标海域的水深条件，以及波浪波高和周期的变化范围已知的情况下，通过三维数值波浪水槽，对此种防波堤的消浪性能与结构尺寸、透空率和波浪条件之间的关系进行研究。

1 防波堤结构与数值模拟方法

1.1 透空防波堤结构形式

透空防波堤的结构形式为带有透浪通道的直立式沉箱结构，根据透浪通道形状的不同可分为错位沉箱和异型沉箱两种结构，其尺寸如图1所示。通过透浪通道的交错设计，使得波浪必须经过多次绕射和反射后才能传播到堤后，从而减小波浪透射。同时能够通过反射波的不规则性和与入射波的相位差，避免与入射波叠加形成驻波，减小堤前的水面震荡[15]。

沉箱的横向与纵向间距a、b可以根据对防波堤透空率的实际需要进行相应调整，透浪通道的轴线间距c反映了防波堤内透浪通道的交错和曲折程度，因此也是影响消浪性能的重要参数。为了使数值模拟的结果能够与本文进行的断面物理模型试验的结果进行直接比较，在数值水槽中采用与物模试验相同的1∶43.75的比尺对防波堤结构尺寸进行缩小。

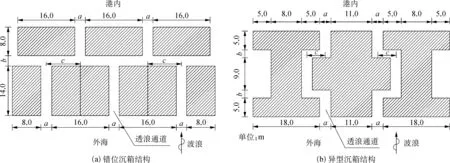
图1 透空防波堤结构原型尺寸

1.2 数值水槽控制方程

通过Fluent建立三维数值波浪水槽，对透空堤的消浪性能进行数值模拟，水槽示意如图2所示，计算区域的水平长度为12.5 m(x方向)，高度为0.8 m(y方向)，宽度为0.8 m(z方向)。数值波浪水槽的控制方程为三维Navier-Stokes方程[16]，包括连续方程和动量方程，其张量表达式为：

(1)

(2)

式中：i，j=1，2，3；ui为第i方向上的速度分量；ρ为流体密度；p为流体压力；gi为第i方向上的重力加速度分量；τi j为黏性应力张量。对于牛顿流体，有：

(3)

式中：μ为水分子黏性系数；σi j为平均应变张量。

计算域内的体积单元由空气和水两种介质组成，在Fluent中设置两相流模型，采用VOF方法对自由水面进行追踪[17]，气液两相界面通过求解体积函数F的连续方程得到。动量方程的离散采用了二阶迎风格式，通过压力隐式的算子分割算法(PISO算法)进行求解[18]。整个数值水槽的计算域划分为约548 000 个六面体单元，并对透浪通道内部和自由水面附近的网格进行了局部加密，网格划分如图3所示。

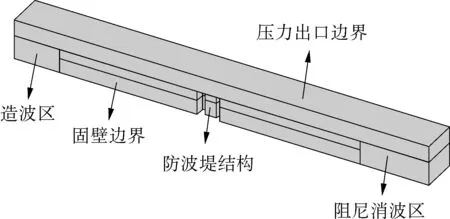
图2 数值波浪水槽示意

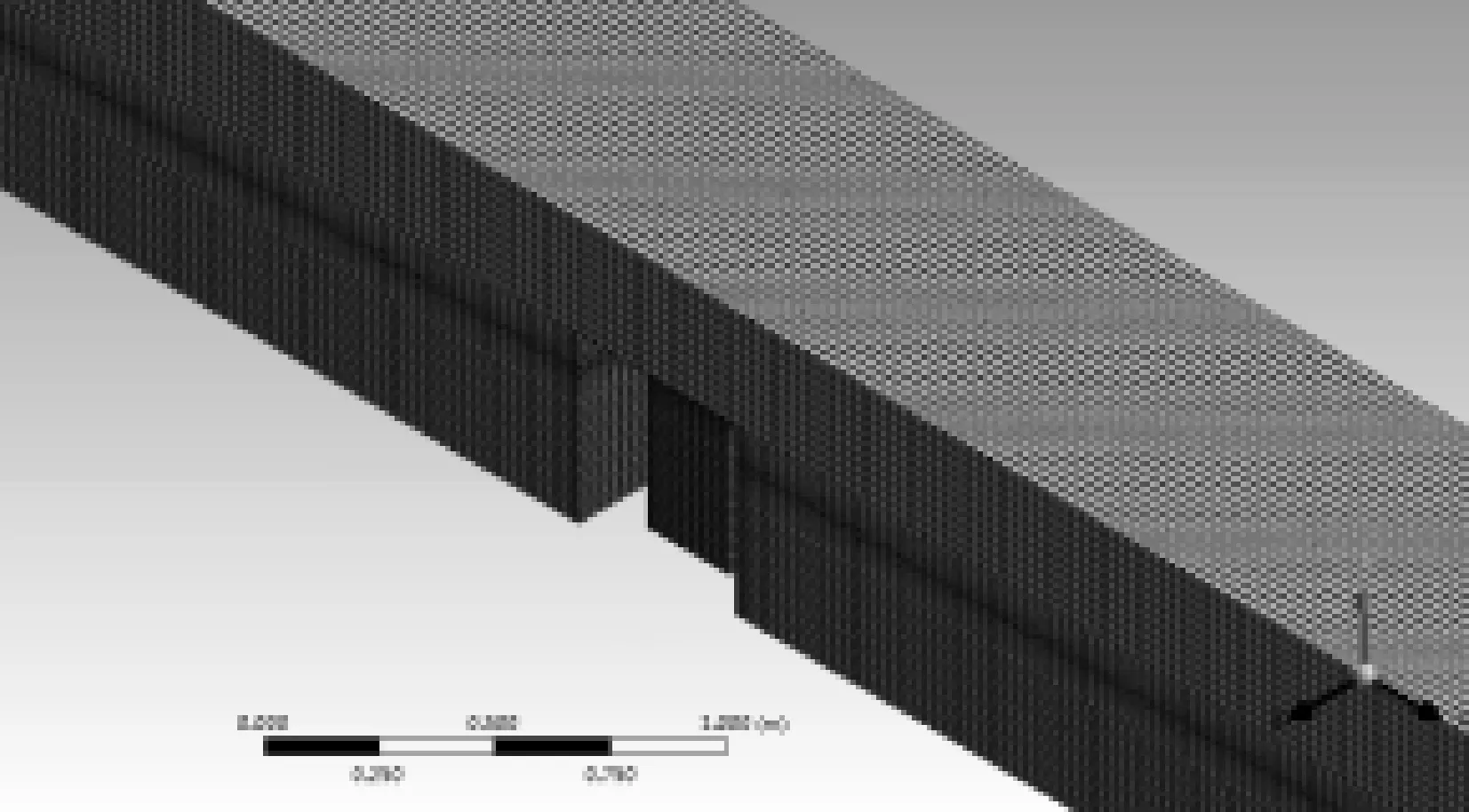
图3 网格划分示意

1.3 边界条件与造波和消波方法

数值水槽顶部为压力出口边界条件。水槽底部、左右两侧及防波堤结构表面为固壁边界条件。水槽前端和末端通过UDF设置边界条件进行造波和消波。数值造波方法采用速度入口边界造波方法，对于线性波，造波边界x=0处的自由水面方程为[19]：

(4)

在自由水面以下，通过UDF程序定义水质点沿x向运动速度u和y向运动速度v为：

(5)

(6)

水槽中单向波浪仅沿x向传播，在z向上没有分量，因此水质点沿z向运动速度w=0。在水槽末端采用人工黏性的方法，设置阻尼层以消除波浪反射[20]。在UDF程序中通过在动量方程中添加阻尼项来实现，阻尼系数μ的取值为：

(7)

式中：Lf为阻尼层的长度，需满足至少一倍的入射波波长，取3.0 m；x0为阻尼层起始位置的横坐标。从阻尼层的起点到终点，阻尼系数μ的值由1逐渐减小至0。

2 数值波浪水槽的验证

2.1 水槽造波能力与消波效果的验证

为了验证数值水槽的造波能力、模拟波浪传播的效果以及阻尼层的消波效果，建立了无结构物的波浪水槽模型。计算了水深d=0.4 m时，波高H=0.08 m、波长L=1.59 m的规则波，数值模拟结果如图4和图5所示。图4为t=15.0 s时刻波面的模拟结果，此时波浪已经充分传播到水槽末端。可以看出，波浪沿水槽传播稳定，且水槽末端消波区域的消波效果良好。图5为x=3.5 m测点处的波面历时曲线，并与理论值进行了比较，结果表明模拟波浪的波高和波形与规则波理论符合良好。

图4 水槽内t=15.0 s时刻波面模拟结果

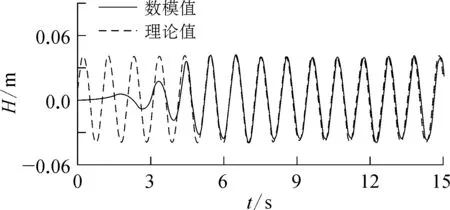
图5 水槽内x=3.5 m测点处的波浪过程线

2.2 波浪对直墙结构作用的模拟与验证

为了验证数值水槽模拟波浪与结构物相互作用问题的准确性与有效性，建立了波浪对直墙结构作用的数值水槽模型，设置光滑直立壁面位于x=6.5 m处。计算了水深d=0.4 m时，波高H=0.08 m、波长L=1.59 m的规则波，数值模拟结果如图6和图7所示。

由理论可知，波浪在直立壁面处应发生完全反射，与入射波叠加形成驻波。图6为半个周期内的波面变化情况，可以观察到明显的波节与波腹。图7为理论波腹点x=6.5 m(直墙前侧)和波节点x=6.1 m(直墙前1/4波长处)的波浪过程线。结果表明，x=6.1 m处仅有微小的水面波动，x=6.5 m处的波高约为入射波波高的2倍，因波高增大，波浪的非线性导致波谷处略有变缓。综上说明了数值水槽的直墙前形成了典型的驻波，数值模拟结果与理论符合良好。

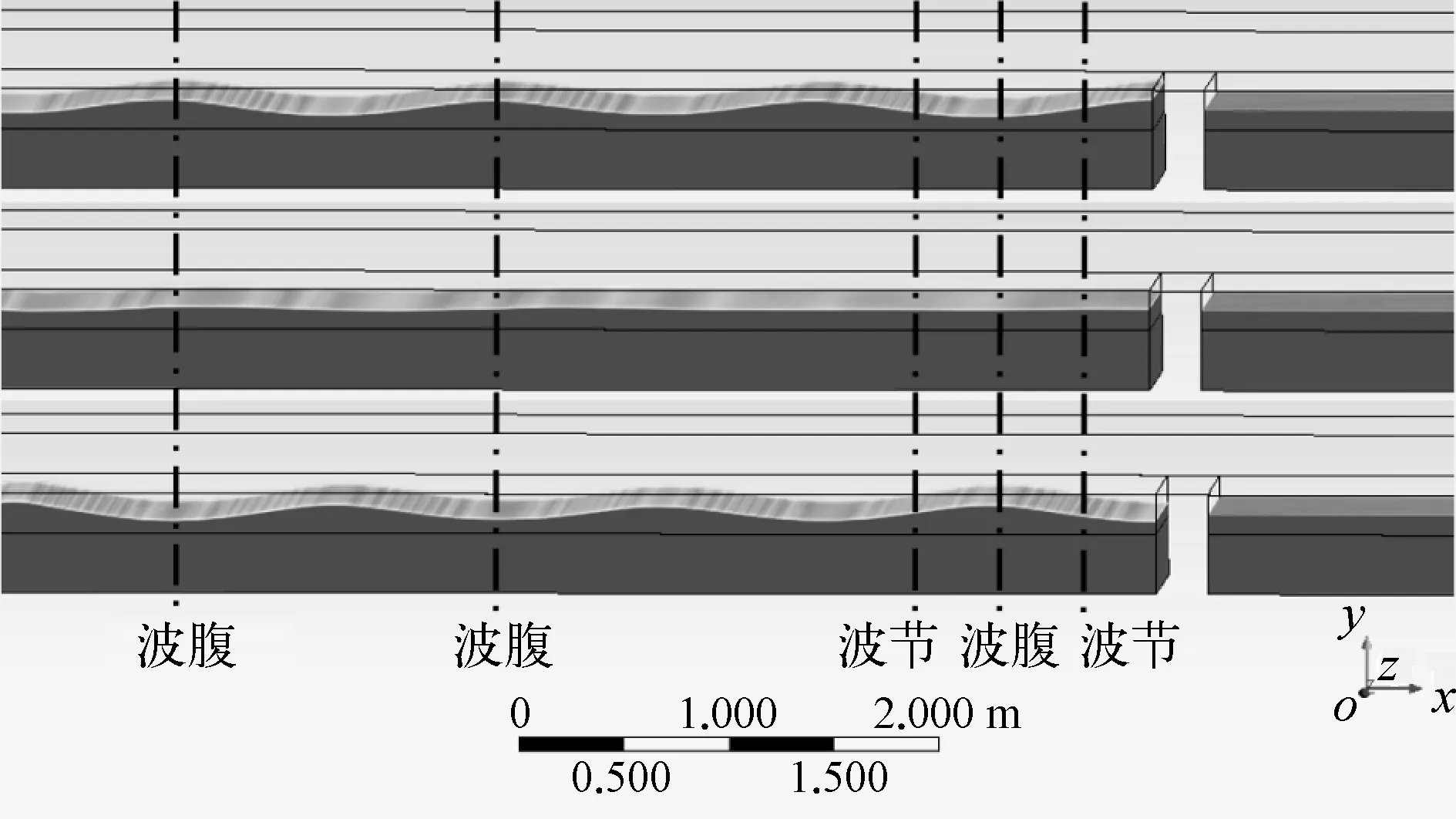
图6 直墙反射水槽内半个周期的波面变化情况

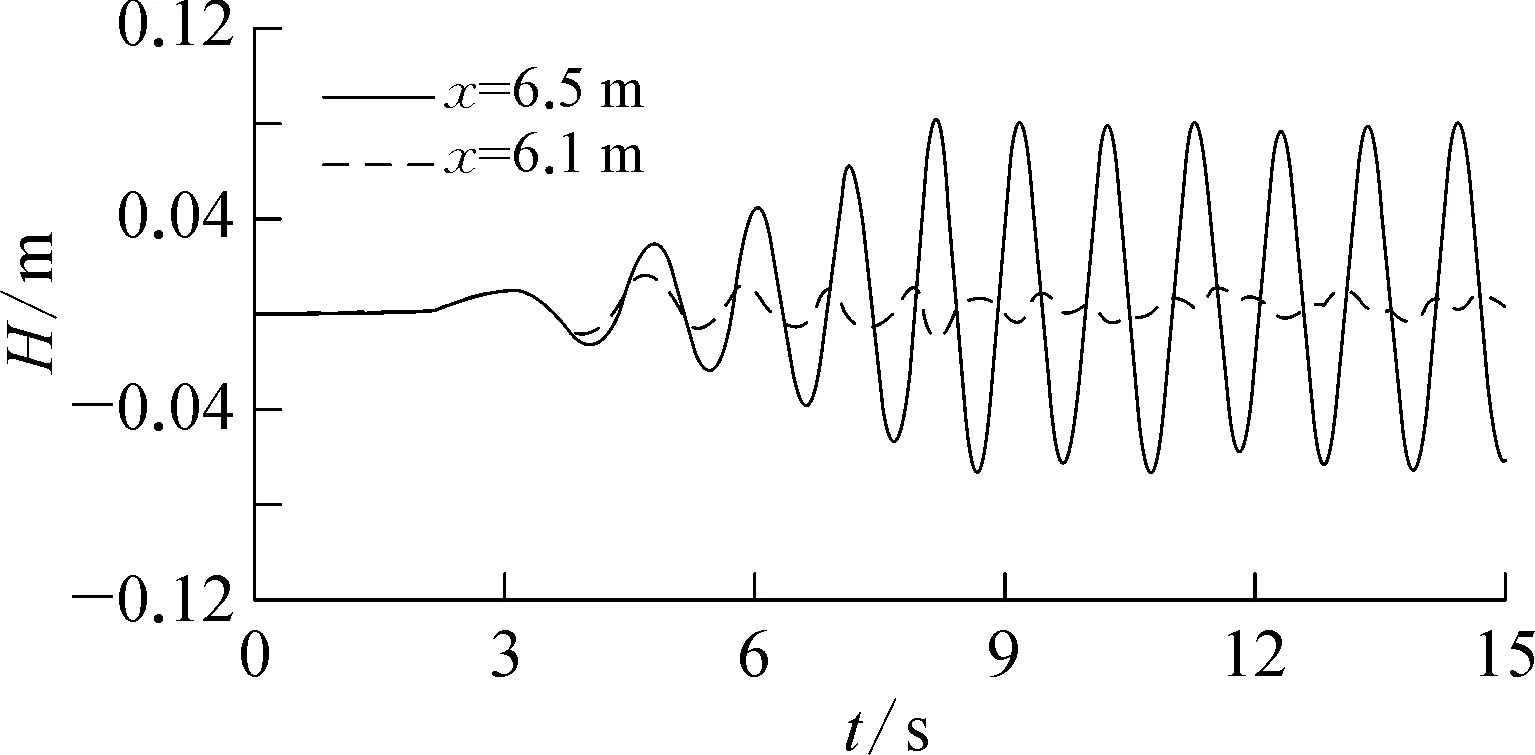
图7 直墙反射水槽内x=6.5 m及x=6.1 m处的波浪过程线

2.3 数值模拟与物模试验结果的对比

为了检验数值模拟结果的准确性，对部分工况进行了物理模型试验。试验在波浪水槽中进行，水槽长22 m，宽0.8 m，高0.8 m，物模试验的比尺为1∶43.75，与数值模拟的比尺相同。试验采用错位沉箱结构的透空防波堤，结构形式如图1(a)所示，其中模型尺寸a为0.068 m、b为0.046 m、c为0.206 m，在防波堤堤后1.0 m处的轴线上设置浪高仪以测量透射波浪的大小。

在水深0.4 m、入射波波高0.06 m、波长1.59 m时，物模试验得到的防波堤堤后透射测点处的波浪过程线如图8中虚线所示。与数值模拟结果对比可以得到，除物模试验中因造波机启动引起的前面数个较小的波浪外，在波形稳定后，物模试验结果与数值模拟结果符合良好。舍去前面较小的波浪，选取稳定部分10～15个波浪的平均波高作为透射波浪的波高，计算得到透射系数Kt为：

Kt=Ht/H0

(8)

式中：H0为入射波波高；Ht为透射波波高。

在水深0.4 m、入射波波高0.06 m、波长0.88～2.29 m时，物模试验与数值模拟得到的透射系数对比如图9所示，计算得到二者的误差范围在3%～24%之间，因此错位沉箱防波堤物模试验与数值模拟所得到的透射系数符合较为良好。

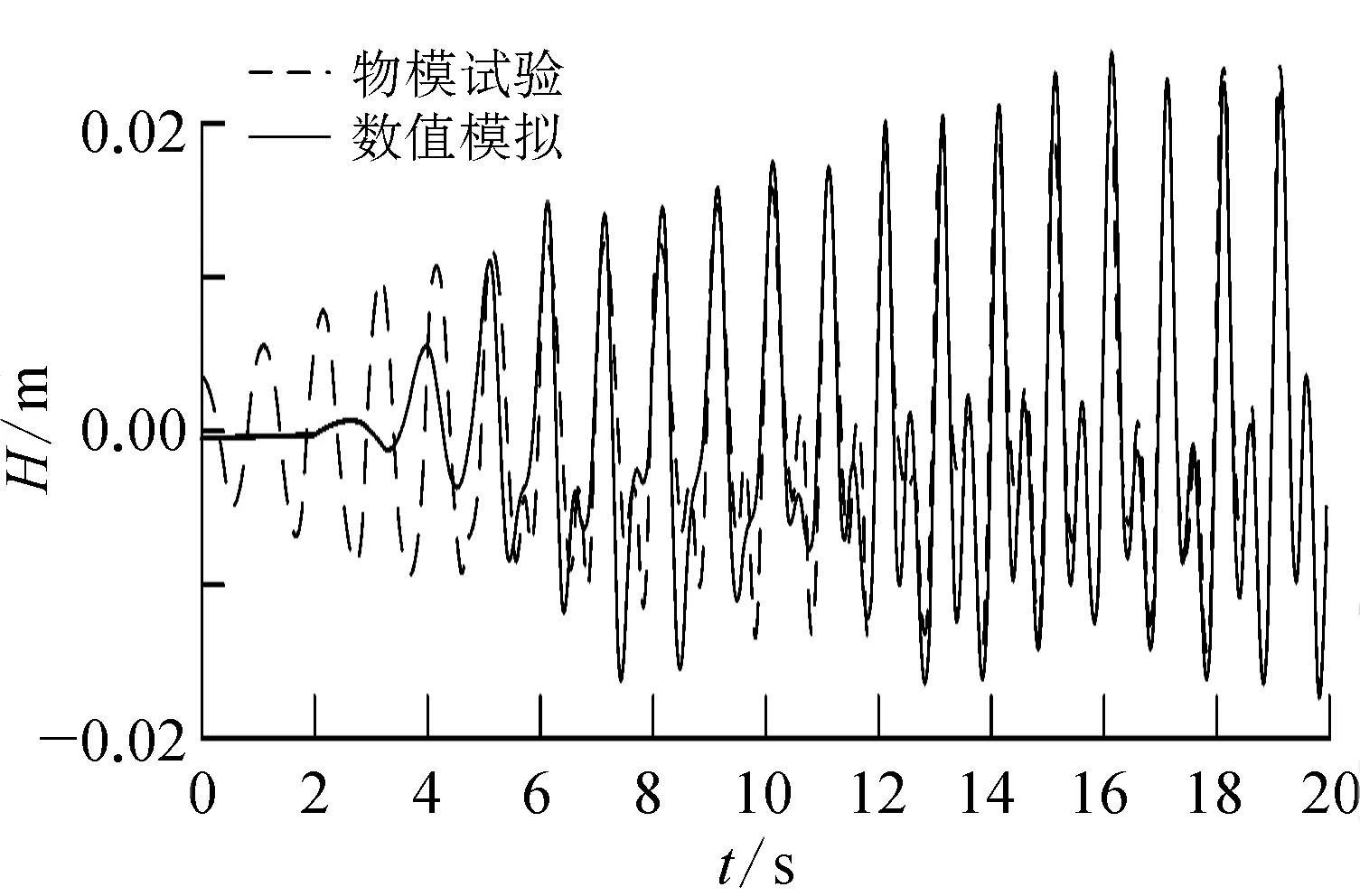
图8 物模试验与数值模拟透射波浪过程线的比较

图9 物模试验与数值模拟透射系数的比较

3 透空堤消浪作用的模拟结果与分析

3.1 波面模拟结果及消浪机理分析

错位沉箱和异型沉箱结构的透空式防波堤，主要都是通过前后交错的透浪通道，阻碍水质点沿波浪传播方向的运动轨迹，使得波浪必须在经过绕射和反射等过程后才能传播到堤后。以H=0.10 m、L=1.11 m的波浪为例，其作用于错位沉箱和异型沉箱防波堤时的模拟结果如图10所示。

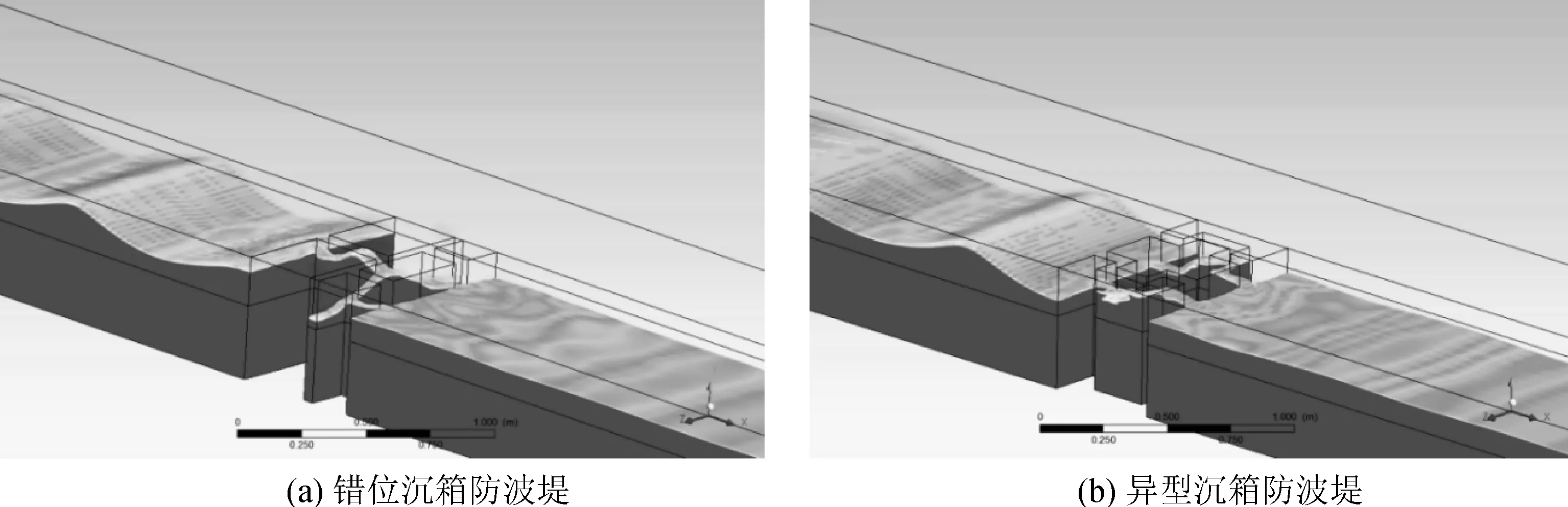
图10 H=0.10 m、L=1.11 m波浪作用的模拟结果

由数值模拟结果可以看出，有部分波浪在防波堤前产生了反射，而进入透浪通道中的波浪通过在透浪通道内的多次的绕射、反射以及相互作用产生的波浪破碎消耗了大量能量，最终只有少部分波浪透过防波堤继续传播。因此这两种结构型式的防波堤都能够起到较好的掩护效果，同时这两种防波堤也均具备一定的透流能力，使得港内外水体能够进行良好的交换。

3.2 透浪通道尺寸对透射系数的影响

为了保证港池内外的水体交换能力，透空式防波堤必然会对波浪产生一定的透射，而透射系数的大小是评价透空堤掩护效果的重要指标。基于三维数值波浪水槽，对两种透空式防波堤共进行了100组不同结构及波况下的数值计算，并重点研究了防波堤的透射系数Kt受透浪通道的尺寸和波浪的波高、波长的影响情况。

根据结构原型尺度，按1∶43.75的比尺进行缩小，取错位沉箱防波堤透浪通道的轴线间距c为0.16～0.24 m；异型沉箱防波堤透浪通道的轴线间距c为0.025～0.16 m。定义防波堤的透空率F为透浪通道总面积与防波堤总平面面积之比。通过调整透浪通道的横向宽度a与纵向宽度b可得，错位沉箱防波堤透空率F的取值范围为0.121～0.190，异型沉箱防波堤透空率F的取值范围为0.127～0.226。根据海域的水深及波浪条件，得到数值计算所采用的水深d为0.4 m，波高H为0.06～0.10 m，波长L为0.88～2.72 m。以上参数的选取基本能够覆盖工程实际中结构和波浪参数的选取范围。对该范围内各工况下的模拟结果做统计分析，得到透射系数与各影响因素之间的关系如图11～14所示。

图11给出了波高为0.08 m，波长分别为1.35 m、1.59 m、1.94 m时，透浪通道间距c=0.21 m的错位沉箱和c=0.16 m的异型沉箱防波堤的透射系数Kt随透空率F的变化情况。结果表明，透射系数Kt随透空率F的增加而有明显的增大，且在本数值模拟选取的透空率范围内，两者近似呈正线性相关。相比较而言，随透空率的增加，错位沉箱结构透射系数的变化幅度更大，而异型沉箱结构透射系数的变化幅度相对较小。图12给出了波高为0.08 m，波长分别为1.35 m、1.59 m、1.94 m时，透空率F=0.190的错位沉箱和F=0.226 m的异型沉箱防波堤的透射系数Kt随透浪通道间距c的变化情况。结果表明，透射系数Kt随透浪通道间距c的增加而有减小的趋势。说明在透浪通道更加曲折时，对减小防波堤的透射系数有一定的帮助。在相同的透空率下，通过调整透浪通道间距，可以使透射系数降低20%～30%。

图11 透射系数Kt随透空率F的变化情况

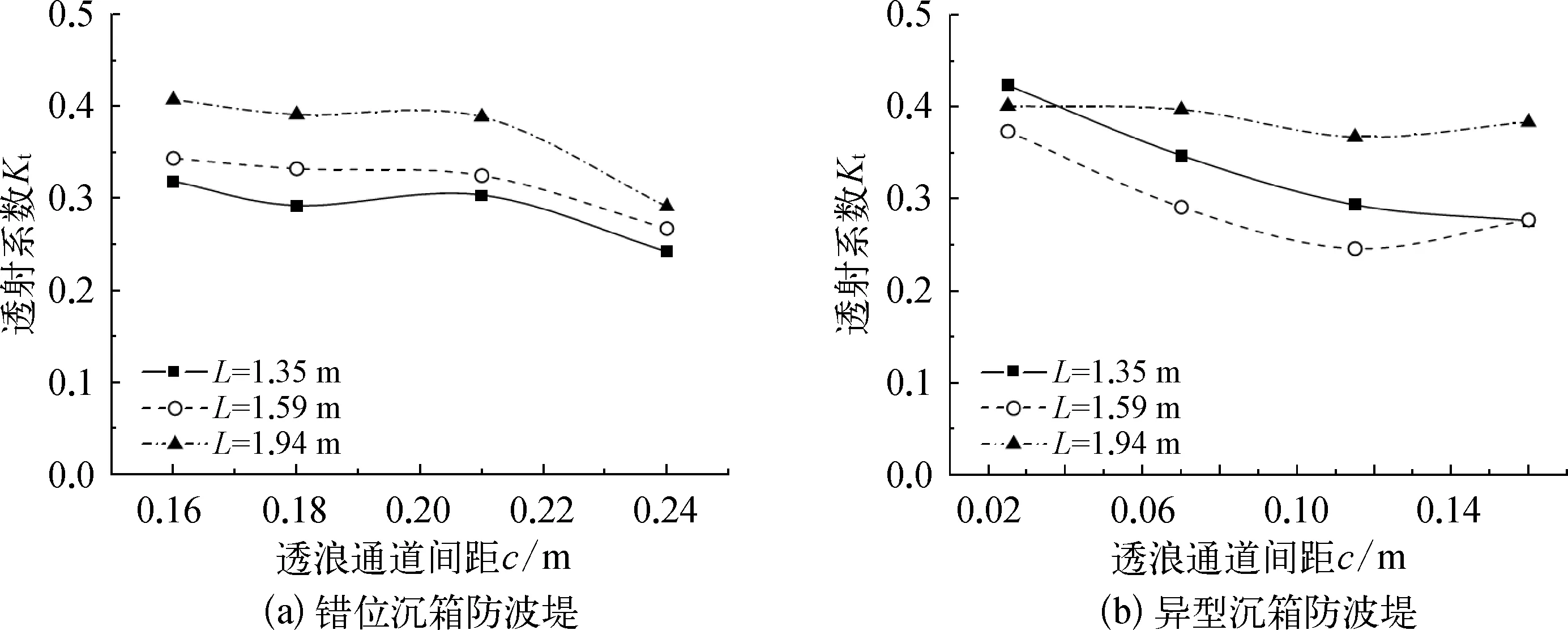
图12 透射系数Kt随透浪通道间距c的变化情况

3.3 波浪特征对透射系数的影响

通过对数值模拟结果的分析表明，除防波堤结构本身的尺寸对透射系数有影响外，同一防波堤对不同波高和波长的波浪的透射系数也是不同的，取无因次化的参数H/d与L/d分析波浪特征对透射系数的影响。图13给出了透空率F=0.190、透浪通道间距c=0.21 m的错位沉箱和透空率F=0.226、透浪通道间距c=0.16 m的异型沉箱防波堤，在波高分别为0.06 m、0.08 m、0.10 m时的透射系数Kt随相对波长L/d的变化情况。结果表明，对于两种结构型式的防波堤，透射系数随相对波长的变化规律大致相同。在L/d小于3.5时，透射系数Kt均随L/d的增加而显著增大。在L/d大于3.5后，透射系数增大的速率逐渐减小，且随相对波长的变化有一定的上下波动。透射系数的最大值出现在L/d为5.0处，对应的Kt约为0.4。

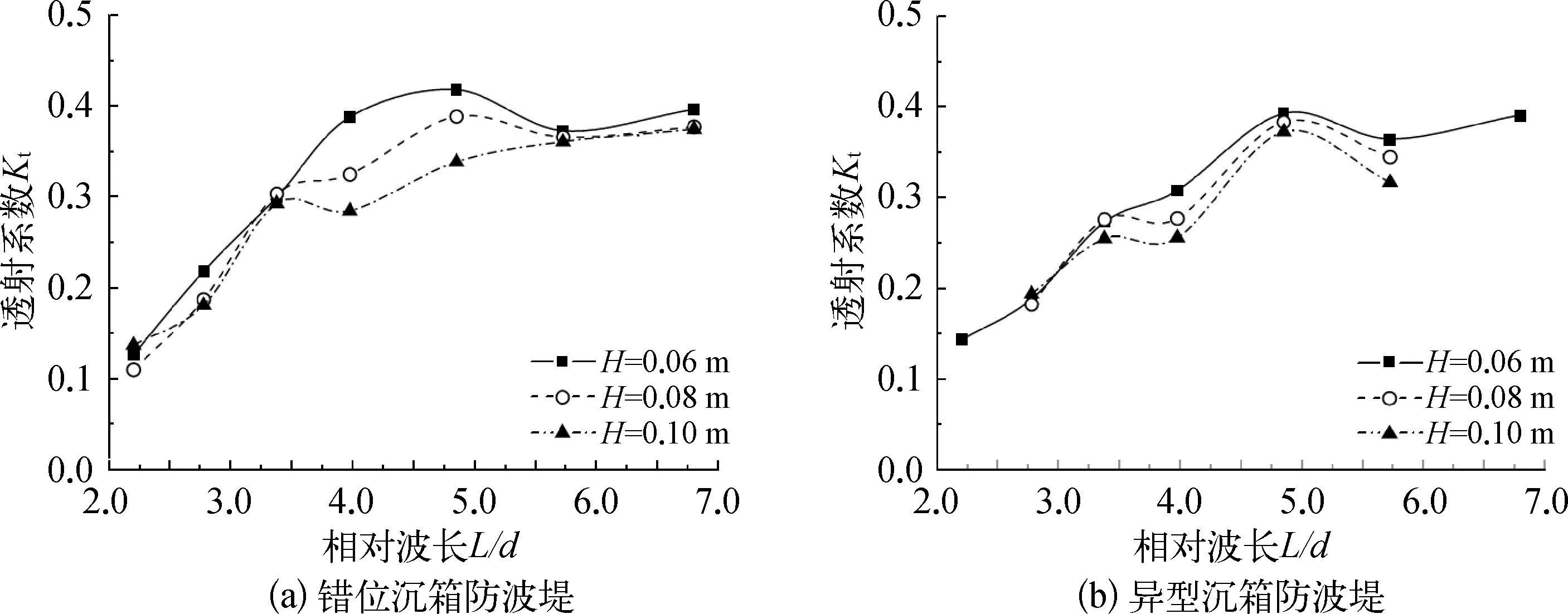
图13 透射系数Kt随相对波长L/d的变化情况

图14给出了上述尺寸的防波堤，在波长分别为1.11 m、1.35 m、1.59 m、1.94 m和2.29 m时的透射系数Kt随相对波高H/d的变化情况。结果表明，对于两种防波堤，透射系数均随相对波高的增大而略有减小，相比较而言，H/d的变化对错位沉箱防波堤透射系数的影响更为明显。在H/d由0.15增大到0.25时，对应不同波长的波浪，错位沉箱防波堤透射系数降低的幅度为3.29%～23.60%，异型沉箱防波堤透射系数降低的幅度为3.08%～16.96%。

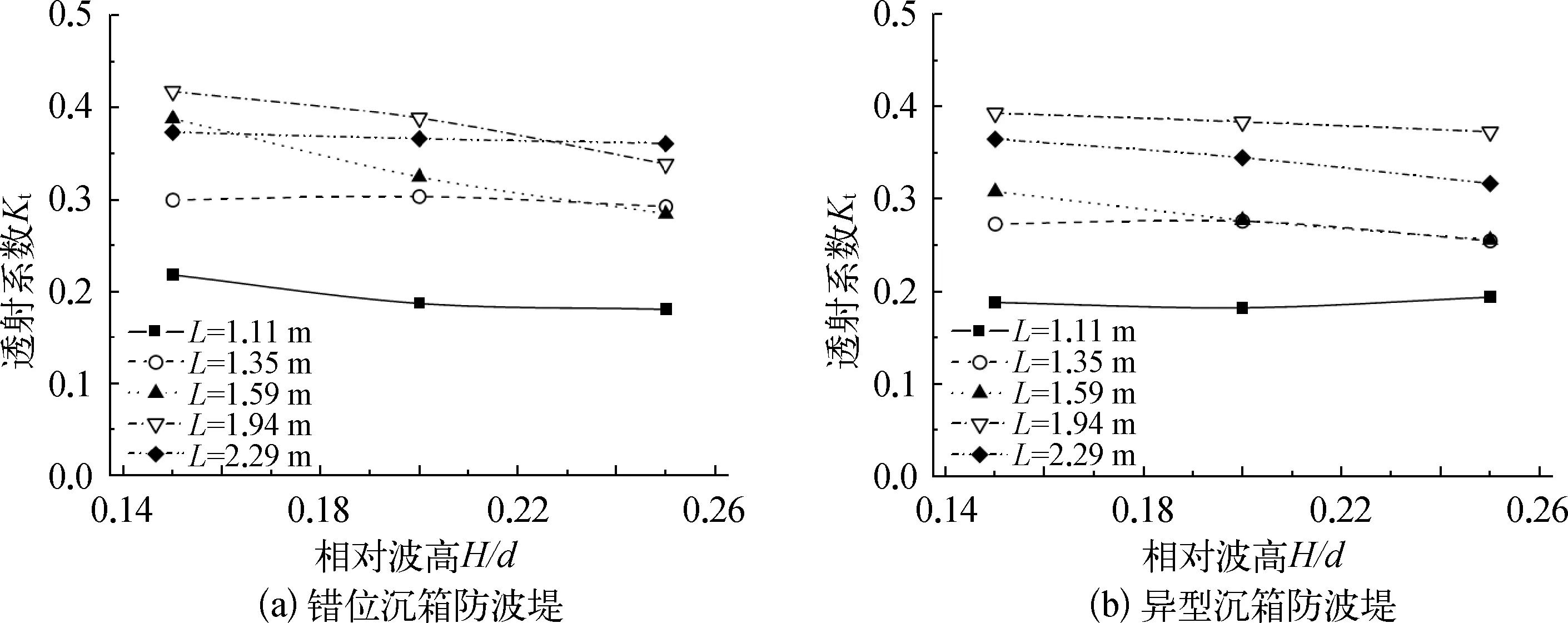
图14 透射系数Kt随相对波高H/d的变化情况

3.4 结构型式对透射系数的影响

错位沉箱和异型沉箱两种结构型式的防波堤对波高为0.08 m，波长分别为1.35 m、1.59 m、1.94 m的波浪的透射系数随透空率F的变化如图15所示，图中实心点表示错位沉箱，空心点表示异型沉箱。可以看出，对同一波浪，在透空率较小时，错位沉箱结构的消浪性能更好；在透空率大于0.16后，异型沉箱结构的消浪性能更好。在错位沉箱的透空率小于0.20或异型沉箱的透空率小于0.24时，可以使得其对绝大部分波浪的透射系数均维持在0.4以下。

对不同结构尺寸及波浪条件下的数值模拟结果，通过最小二乘法拟合得到了两种透空式防波堤对于波浪透射系数的经验公式。对错位沉箱结构，有：

(9)

对异型沉箱结构，有：

(10)

式中：Kt为透射系数；F为透空率；c为透浪通道间距；L为波长；H为波高；d为水深。

经验公式计算结果与数值模拟结果的比较如图16所示，可以看出二者基本吻合。透射系数的计算误差大部分能够控制在0.05以内，因此本文给出的经验公式可以较为准确的计算错位沉箱和异型沉箱结构防波堤在一定的水深和波浪作用下的波浪透射系数。

图15 不同结构型式防波堤的透射系数Kt

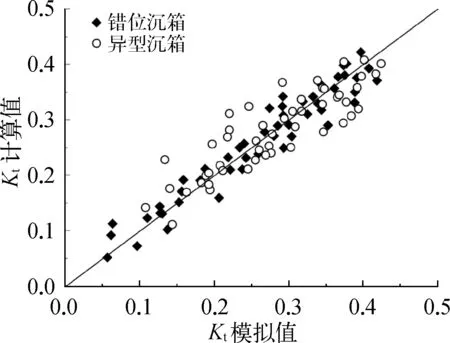
图16 经验公式与数值模拟结果的对比

4 结 语

基于Fluent求解器建立了三维数值波浪水槽，对数值水槽的造波与消波能力、模拟波浪与直墙结构作用问题的准确性进行了验证，并与透空堤物模试验进行了对比。在此基础上，利用数值水槽分别模拟了规则波与错位沉箱和异型沉箱防波堤的相互作用。得到以下结论：

1) 两种透空防波堤的消浪机理均为使进入透浪通道中的波浪通过多次绕射、反射以及相互作用产生的波浪破碎，从而消耗波浪能量。

2) 水深和波浪条件一定时，两种防波堤的透射系数Kt与透空率F均呈正线性相关。通过增大透浪通道间距c，可以使相同透空率下的透射系数降低20%～30%。

3) 在L/d小于3.5时，Kt随着L/d的增加而显著增大，L/d大于3.5后，Kt增大的速率减缓，最大值出现在L/d为5.0处。H/d的变化对Kt的影响相对较小。

4) 在透空率F>0.16后，异型沉箱防波堤的消浪性明显优于错位沉箱。在错位沉箱F<0.20或异型沉箱F<0.24时，可使绝大部分波浪的透射系数维持在0.4以下。