立柱直径比对四立柱平台涡激运动性能影响的数值研究
2021-02-02陈元鑫寇雨丰林志良刘明月
陈元鑫,寇雨丰, 2,林志良, 2,刘明月, 2
(1. 上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室,上海 200240; 2. 高新船舶与深海开发装备协同创新中心,上海 200240)
浮式海洋平台是深海钻井勘探、油气开采、生活补给的重要设施。在洋流作用下,无论是单柱式平台(圆筒形FPSO、Spar),还是半潜式平台(semi-submersible)和张力腿平台(TLP)等典型的多立柱平台都容易产生涡激运动(vortex-induced motion,简称VIM)。在一定条件下的定常来流绕过非流线型的柱状物体时,由于流体的黏性及逆压作用,会在其后方周期性地脱落出旋转方向相反、交替出现的漩涡;漩涡脱落激发垂直来流方向的升力和沿着来流方向的拖曳力,这种周期性的激励力使柱体发生振动,随之改变了尾流场,这种柱体与流体相互作用是复杂的流固耦合作用。涡激运动不仅导致平台的运动幅度增大对生产不利,这种周期性的运动还严重影响锚链和立管系统的使用寿命,已经引起了广泛研究和关注。
Rijken和Leverette[1]开展了方形立柱半潜式平台涡激运动特性试验,研究发现了涡激运动具有锁定现象,即保持平台质量和系泊设置不变的条件下,在一定来流速度范围内半潜式平台发生共振,涡激运动的响应振幅和跨零周期基本不变。Goncalves等[2]通过模型试验得到了四方柱半潜式平台涡激运动响应与折合速度、来流角度之间的关系,锁定现象出现在折合速度Ur=7和8时,此时平台横向运动达到最大值,而且横荡运动周期与平台横向运动固有周期基本一致。研究结果还表明对于四方形立柱的半潜式平台而言,横向运动响应幅值最大出现在30°和45°流向角条件下,而在0°流向角时首摇幅值最大。Zhao和Chen[3]采用SST k-ω湍流模型对流向角为0°、15°、30°、45°,间距比等于3,折合速度1~20四圆柱的流向及横向涡激运动进行了数值模拟研究。研究发现,0°流向时横向振幅最大,四个典型流向角下,横向振幅随折合速度的变化曲线基本吻合。15°流向时,锁定区间最大,为3≤Ur≤12;45°流向锁定区间最小,为2≤Ur≤4;0°流向时,在3≤Ur≤9锁定区间内,整体涡激运动是周期规则的。田辰玲等[4]用DES方法对三立柱轻型半潜平台涡激运动特性进行了数值模拟,结果表明0°流向角时首摇运动达到最大响应幅值,在折合速度7.0≤Ur≤10.0区间发生锁定现象。
当前涡激运动的研究对象主要集中在立柱直径一致的平台上,这些平台在结构上基本都具有对称性。目前,非对称半潜式平台也已经投入工程使用。中集来福士海洋工程有限公司建造了非对称无横撑半潜式平台[5],该种新型平台的下船体包括第一浮筒和第二浮筒,其中第二浮筒的体积小于第一浮筒,整体结构是关于中纵剖面不对称的。曹义军[6]对这种非对称无横撑半潜式平台的水动力性能开展研究,发现如果两个浮筒的首尾存在尺寸和形状上的差异,平台的运动将发生垂荡横摇或垂荡纵摇耦合,且差异越大,耦合越明显。非对称半潜平台在特定情况下可以提高平台水动力性能,如张洪达所设计的非对称半潜式海洋平台[7],其具有两种尺寸的立柱,立柱直径较大的一侧为主浮箱,利用该侧的前排浮箱和后侧浮箱产生有利的波浪干扰,可以有效地防止整个平台在波浪中运动时产生的螺旋式垂荡运动,进一步改善了半潜式平台的水动力性能和稳性性能。目前关于非对称平台的研究成果多是关于平台总体水动力性能的,而针对非对称平台涡激运动的研究才刚刚起步,其中Liu等[8]对不同截面形式立柱组合的非对称平台进行了涡激运动方面的研究,采用CFD方法展示了非对称平台的涡激运动仍是不可忽视的运动响应。
以四圆柱平台为基础,缩小其中相邻两个立柱的直径,建立具有两种直径的非对称四立柱模型,定义直径比为原立柱直径和缩小后直径之比,通过CFD方法对直径比1.0、 1.5和2.0的三种立柱组合在0°和180°两个流向角下的涡激运动响应进行研究,主要分析了直径比1.5和2.0的平台涡激运动的横荡、艏摇响应特性,研究了直径比和流向角对非对称平台涡激运动性能的影响。
1 研究对象及参数定义
1.1 物理模型简化
对具有不同直径立柱组合的非对称半潜式平台的涡激运动性能进行研究。由于主要考虑立柱直径比的影响,因此将该问题简化为二维问题。在CFD计算模型中,忽略平台浮箱、横撑等结构的影响,选取平台四立柱的截面为研究对象,在四立柱截面上施加水平系泊系统来进行定位。计算域如图1所示,定义大立柱直径为D,小立柱直径为d。选用1.0、1.5、2.0这三组直径比和两组流向角,把大直径立柱在上游的情况定义为0°流向角,小直径立柱在上游的情况定义为180°流向角。设计0°和180°两个流向角的主要原因是已知对于同一直径的四圆柱平台在该两组流向角下是完全对称的,都会出现显著的“锁定”现象,而改变其中同侧两个立柱直径后,平台在这两个流向角下呈现的响应特性有助于分析直径比对涡激运动特性的影响,并且可以进一步分析对比这两个流向角下不同直径立柱组合的平台的涡激运动性能。
模型中大立柱直径D=0.39 m,与文献[9]一致,不同直径比立柱组合中大立柱直径保持不变,且立柱中心距不变。

图1 物理模型及计算域
1.2 参数定义
立柱直径比定义为:
(1)
特征长度定义为:
(2)
雷诺数和折合速度相应的取为:
(3)
(4)
其中,u是来流速度,T是平台在静水中横荡自由衰减运动的固有周期,n为运动黏性系数。
为更好地分析比较,按照单一直径分别定义的折合速度:
(5)
(6)
涡激运动响应与折合速度密切相关,锁定区间也是依据折合速度来分析。
在研究VIM响应特性时需要知道平台的横荡、纵荡以及艏摇的响应,一般定义两种无量纲数作为参数,即最大响应幅值和标称响应幅值,以横荡为例:
最大响应幅值:
Maximum(A/D)=[Y(t)max-Y(t)min]/2Dr
(7)
标称响应幅值:
(8)
式中:Y(t)是横荡时历,σ是标准差。
2 计算模型
2.1 涡激运动控制方程
涡激运动是一种复杂的流固耦合现象,在流体流经柱体时,由于实际流体有黏性,柱体表面的流体会发生分离,柱体后方会产生周期性的漩涡脱落,其表面压力也发生周期性的变化,从而产生周期性的作用力,表现为来流方向上的阻力和垂直来流方向的升力,因此诱发了柱体的振动,柱体的振动又改变了附近的流场。在全流场中,满足不可压缩黏性流体的连续性方程和动量方程:
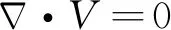
(9)
(10)
式中:ρ为流体密度;P为压力;V为速度;F是质量力;ν为运动黏性系数。
2.2 数值模拟方法
在研究中所有数值模拟都是用CD-adapco提供的有限体积CFD程序STAR-CCM+进行的。在STAR-CCM+软件中,选用了RANS法中的Spalart-Allmaras湍流模型。模拟中使用的动网格技术(dynamic fluid-body interaction,简称DFBI),STAR-CCM+中的DFBI适用于求解海洋结构水动力问题中旋转运动响应较小的情况,大部分涡激运动的艏摇响应比起横荡相对较小。
2.3 模型参数、网格和边界条件
涡激运动主要观察的是尾流场,因此在计算域的建立上,尾部的流场区域较大,以四个立柱的中心为坐标原点,计算域具体尺寸为12.56 m×18.84 m。λ=1.0时立柱直径按照文献[9]中的试验模型给定,λ=1.5和λ=2.0时的其中两个立柱直径经缩小得到。立柱平台模型的具体参数如表1所示,其中λ=1.5和λ=2.0的数据根据λ=1.0计算得出。等效系泊系统,即四个水平弹簧,用于为模型提供水平恢复力,与x、y轴都保持45°,每个弹簧的刚度系数为0.184 N/m。

表1 三种比例下的模型质量和z向惯性矩
考虑到计算域和立柱模型较简单,因此采用较为规整的Trimmer网格模型,Trimmer网格是一种半结构型网格,相对于四面体网格其网格正交性优势明显,相对于六面体网格其对复杂几何体的适应性更强[10]。立柱平台周围用三层网格加密,边界层的模拟方面,根据边界层总厚度、靠近壁面第一层厚度和层数来控制,y+值为1左右。计算域整体网格和圆柱附近网格如图2所示。

图2 整体和局部网格划分
数值计算需要给出合理的边界条件,才可以模拟出合理的流场并给出数值解。此模拟中建立的计算域,左侧面设为速度入口边界条件,右侧面设为压力出口边界条件,其余面设为对称边界条件,四立柱面设为无滑移壁面边界条件。
2.4 工况设置
表2给出了所有进行数值模拟的工况,其中λ=1.0时0°和180°流向角是完全一致的工况,因此无需重复进行模拟。

表2 计算工况
3 自由衰减试验及数值模拟方法验证
3.1 自由衰减试验及网格收敛性验证
在来流速度为0的条件下,将四立柱平台初始横向速度设置为0.2 m/s后释放,得到λ=1.0时平台横荡自由衰减结果。在STAR-CCM+中建立网格时,基本尺寸(base size)是一个全局控制变量,保持网格其他设置不变,改变基本尺寸的值可以改变网格大小及总网格数。采用三种基本尺寸的值,分别为0.8 m、0.4 m、0.2 m,总网格数分别为24 000、77 000、270 000左右。图3(a)结果显示了三种网格下得到的横荡自由衰减频率结果分别为0.116 7 Hz、0.119 8 Hz、0.123 0 Hz。0.4 m和0.2 m得到的频率差值百分比为2.67%,验证了网格收敛性良好,后续数值模拟采用基本尺寸为0.4 m的网格设置。
图3(b)、(c)分别展示了基本尺寸为0.4 m情况下的衰减时历曲线和傅里叶变换结果。根据文献[4]中对时间步长的测试和验证中,时间步长取T/200可保证足够的精度和收敛,其中T为平台在静水中的横向自由衰减周期。

图3 λ=1.0时横荡自由衰减结果和傅里叶变换结果
对于λ=1.5,2.0的四立柱平台使用类似方法进行模拟,经处理后得到的周期和时间步长如表3所示。

表3 三种比例下平台的横荡固有周期
3.2 直径比为1.0时数值模拟结果

图4 横荡标称幅值数值模拟结果与试验结果比较[9]
为了验证数值模拟的可靠性,首先将λ=1.0的横荡标称响应幅值数值模拟结果与试验结果[9]进行比较。从图4中可见,当Ur=4时,数值模拟结果的横荡标称响应幅值很小;当Ur>4时,幅值迅速增大;在6
4 结果与分析
4.1 三种不同直径比平台在0°流向角下的涡激运动特性
图5(a)展示了三种不同立柱组合在0°流向角下的横荡标称响应幅值。首先,λ=1.0的标称振幅显示出如前所述的“锁定”现象,锁定区域为6≤Ur≤8。λ=1.5时横荡标称响应幅值和λ=1.0的结果相比,基本规律相似,在广义折合速度定义下出现了滞后的锁定区域6≤Ur≤9,横荡标称响应峰值基本相同。而对于λ=2.0,当4≤Ur≤5时,横荡标称响应幅值很小,但仍在增大;当Ur>5时,标称幅值迅速增大;当8≤Ur≤12时,标称振幅仍在0.6以上,处于稳定状态,最大值在Ur=10左右取得;当Ur>12时,标称幅值迅速回落,由此得到了一个更宽的锁定区间,8≤Ur≤12,并且达到了更大的标称响应峰值。更宽的锁定区间原因可能是,在λ=2.0的情况下,当Ur=12时,由大直径确定的UD为8.5,仍在单一直径四立柱平台的锁定区域(6~8)附近,由于其上游两个立柱处在这个锁定区间附近而导致整个四立柱结构的横荡响应依然处于较高的水平。
艏摇标称响应幅值也呈现了一定的规律性,如图5(c)所示,在已研究的折合速度下,艏摇响应幅值随折合速度增大而先增大后减小,但其“锁定现象”不如横荡响应幅值显著,并且λ=1.0时的艏摇标称响应幅值要大于λ=1.5和λ=2.0时的幅值,可能的原因是上游大直径圆柱脱落的涡对下游小直径立柱产生了转动上的抑制作用。
图5(b)是三种不同直径比平台在0°流向角下的横荡最大响应幅值。这种无量纲量与相对应的标称统计量在规律上呈现统一性,但是数值上要大出很多,由于在涡激运动分析中,一般尽可能选取平台响应稳定或较为稳定时分析其统计特性,因此标称响应幅值在呈现统计特性时更有优势,后面的分析和结论也主要针对标称响应幅值。
图5 0°流向角下横荡、艏摇响应幅值
图6展示了λ=1.0时折合速度为7,8;λ=1.5时折合速度为6,7,8,9和λ=2.0时折合速度为7,8,10,11的横荡运动时历曲线以及对应的傅里叶变换结果,傅里叶变换结果图中垂直的点划线为平台的横荡固有频率。可以看到在这几个折合速度下,两种直径比平台都处在各自的锁定区间内,横荡响应频率与平台横荡固有频率接近或基本一致。
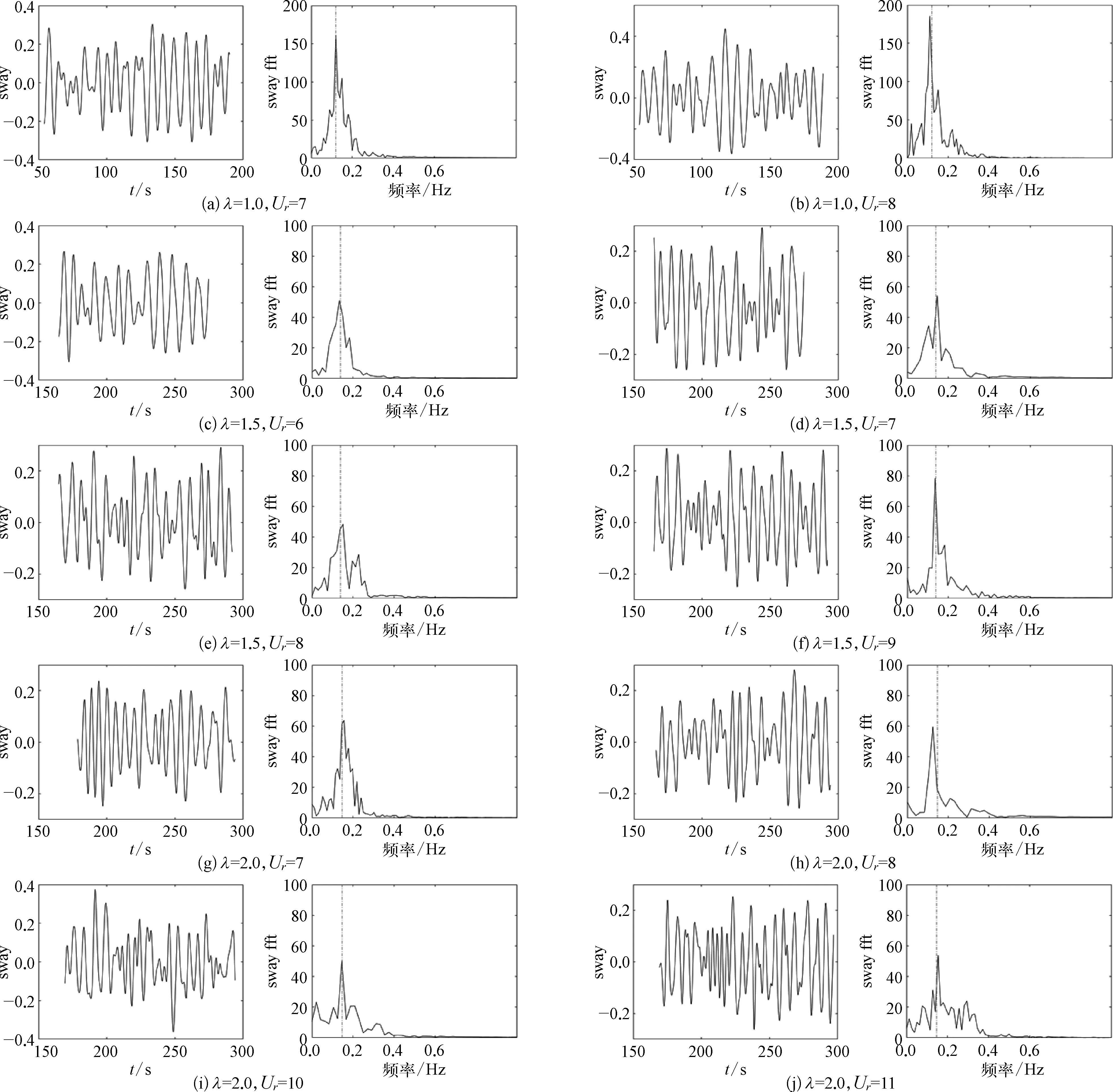
图6 0°流向角下横荡标称响应时历及傅里叶变换结果
4.2 三种不同直径比平台在180°流向角下的涡激运动特性
图7(a)展示了三种不同直径比平台在180°流向角下的横荡标称响应幅值。由于λ=1.0的平台是完全对称的,因此180°流向角的情况与上面提到的0°流向角的情况相同。不同圆柱直径的平台相对于y轴是不对称的,180°流向角意味着来流首先遇到小直径立柱。λ=1.5时,当Ur=4时,横荡标称响应幅值很小;Ur>4后,幅值迅速增大,在6~7之间达到峰值;Ur>7后,幅值迅速回落,但在8~10之间保持稳定趋势;Ur>10后,振幅又逐渐减小,至Ur=12时,响应幅值减小到0.3以下。这个结果可以结合折合速度来解释。5≤Ur≤7对应6.1≤Ud≤8.6,小直径立柱首先进入6~8锁定区间范围内,整体结构的横荡响应幅值保持较大的水平,Ur>7后,幅值回落,然而由于8≤Ur≤10对应6.5≤UD≤8.2,大直径立柱折合速度满足6~8范围,此时整体横荡响应呈现稳定趋势,直到Ur>10后,横荡振幅才完全回落。此外,λ=1.5情况下的最大值略小于λ=1.0的最大值。λ=2.0的情况则较为不同。当4≤Ur≤5时,横荡标称幅值很小;当Ur>5时,幅值迅速增大,在7~10之间保持较大值,峰值出现在9~10之间;当Ur>10时,标称振幅逐渐减小,对比另两种直径比的情况,λ=2.0平台的“锁定”区间范围为更宽的7~10,而横荡标称响应幅值的最大值却是最小的。
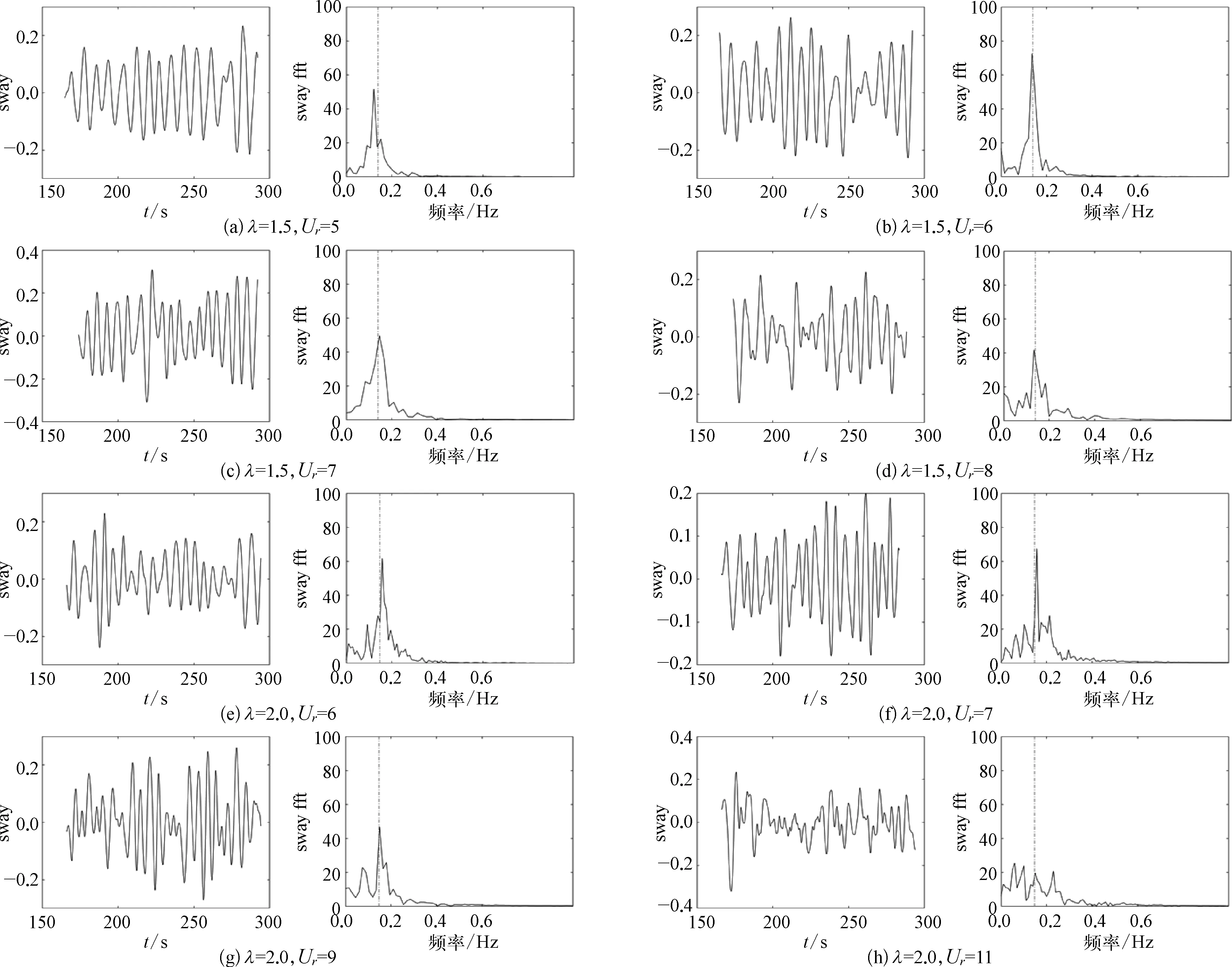
图7(c)展示了三种不同直径比平台在180°流向角下的艏摇标称响应幅值,λ=1.5和λ=2.0的艏摇标称响应幅值在Ur<6时比λ=1.0时幅值小,而6 图7 180°流向角下横荡、艏摇响应幅值 图8展示了λ=1.5时折合速度为5,6,7,8和λ=2.0时折合速度为6,7,9,11的横荡运动时历曲线以及对应的傅里叶变换结果,同样的,傅里叶变换结果图中垂直的点划线为平台的横荡固有频率。可以看到在图8(a)~(g)这几个折合速度下,两种直径比平台都处在各自的锁定区间内,横荡响应频率与平台横荡固有频率接近或基本一致,图8(h)所示的折合速度下已不再锁定区间内,横荡响应频率与平台横荡固有频率无对应关系。 图8 180°流向角下横荡标称响应时历及傅里叶变换结果 流向角(0°和180°)对平台涡激运动特性最显著的影响是横荡响应特性的差异,总体来看,在0°和180°两种情况下都会出现“锁定”现象,而大直径立柱在前还是小直径立柱在前则导致了横荡运动中的差异,大直径立柱在上游时涡激运动响应比其在下游时更显著。 对于λ=1.5的情况,如图9(a)所示,在4≤Ur≤5的范围内,横荡标称响应幅值在0°和180°的流向角下几乎相同;当6≤Ur≤7时,180°流向角下的横荡标称响应幅值大于0°的幅值并且达到峰值,此时起决定性作用的是靠上游的小直径立柱;当7 而0°和180°流向角下艏摇标称响应特性则呈现出完全不同的趋势,如图9(b)所示,除Ur=5时180°流向角所造成的艏摇响应幅值略小于0°对应的幅值外,其余所有折合速度下均为180°对应艏摇幅值显著大于0°艏摇幅值且有双峰的趋势。结合图5(c)及图7(c)对直径比为1.5时的艏摇响应讨论内容,可以合理猜测上游先遇到大直径立柱对于下游小直径的转动总是呈现抑制作用,从而对整个平台的艏摇运动有抑制作用,而上游先遇到小直径立柱对下游大直径立柱转动作用则会有抑制和促进两种,取决于整体流场的结构。 图9 λ=1.5时平台在0°和180°两个流向角下横荡和艏摇标称响应幅值 对于λ=2.0的情况,流向角(0°和180°)对涡激运动中横荡标称响应的影响在峰值方面随着直径比增大而更加显著。如图10(a)所示,在4≤Ur≤6时,0°和180°流向角下横荡响应幅值基本一致保持增长的趋势,但是在Ur>6之后, 0°流向角下的响应幅值显著超过了180°情况下的幅值,而整个锁定区间的宽度却是基本一致的,两者的峰值基本都在Ur=10附近,此时UD=7.1,Ud=14.1,可见,当直径比比较大时,大直径立柱无论在上游或是下游,都在涡激运动中起着更为决定性的因素,而流向角决定着幅值峰值的差异,且这种差异随直径比的增大而增加。 图10 λ=2.0时平台在0°和180°两个流向角下横荡和艏摇标称幅值 图10(b)可以看出λ=2.0时两个流向角下对应的艏摇标称响应幅值在4≤Ur≤6范围内都保持增长且幅值相差不大,在6≤Ur≤10范围内180°下的幅值超过了0°的幅值,在Ur≥10后两者又基本回到同一水平上。 将平台简化为二维四立柱模型,通过数值模拟的方法,对直径比为1.0、1.5和2.0的立柱组合在0°和180°两个流向角下进行多组折合速度下的数值模拟,主要从平台VIM的响应幅值、响应频率出发,结合给出的广义折合速度定义,分析了两种直径立柱的存在对平台涡激运动响应关键特征的影响。得到主要结论如下: 1) 在0°流向角下,直径比为1.5和2.0时平台的横荡响应幅值仍存在锁定区间,在广义折合速度定义下,锁定区间范围变宽且滞后。直径比为1.5的平台横荡标称响应幅值峰值与直径比为1.0的平台响应峰值差别不大;直径比2.0时,平台的横荡标称响应幅值峰值与直径比为1.0的平台响应峰值相比显著增大。 2) 在180°流向角下,直径比为1.5和2.0时平台的横荡响应幅值仍存在锁定区间。直径比为1.5时平台横荡响应幅值峰值比直径比为1.0时的峰值略小;直径比为2.0时平台横荡响应幅值峰值比直径比为1.0,1.5时更小,“锁定”的区间范围会更加宽且更滞后。 3) 对于拥有两个尺寸立柱直径的平台,流向角对平台横荡运动影响非常显著。上游是大直径立柱的平台(0°流向角)横荡特性更接近λ=1.0的情况,而下游是大直径立柱的平台(180°流向角)则会产生较宽但是峰值较小的锁定区间,且这种差异随着直径比的变大而变得更显著。 本文的工作初步探索了不同直径立柱组合的四立柱平台在典型流向角下的涡激运动响应特性,对后续相关研究工作的开展具有良好的指导意义。未来可以建立更完备的三维模型进行数值计算以得到定量的结论,获取完整的流场信息,并且与运动响应结合起来,揭示不同直径的立柱组合对平台涡激运动的作用机制和规律。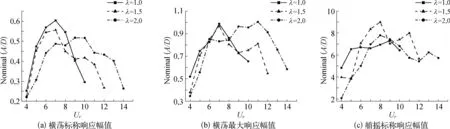
4.3 不同流向角(0°、180°)对两直径非对称四立柱平台涡激运动特性的影响


5 结 语
