分段双加权伪概周期函数的复合定理

宋 娜，夏正德

中北大学 理学院，太原 030051

文献[1]推广了伪概周期函数，介绍了加权伪概周期函数及其相关性质．许多的工作都是围绕着微分方程的加权伪概周期解展开的[2-9]．文献[10]给出了双加权伪概周期函数的概念，进一步推广了伪概周期函数．随着脉冲微分方程的发展，概周期理论得到进一步的发展，分段伪概周期函数、分段加权伪概周期函数与分段双加权伪概周期函数相继被提出[11-13]．关于微分方程，数学工作者做了许多的工作[14-24]．本文的工作是对分段双加权伪概周期函数[25]研究的延续，主要介绍了分段双加权伪概周期函数的复合定理，以及双加权伪概周期函数与双加权伪概周期序列之间的关系．

1 分段双加权伪概周期函数

加权函数具有如文献[2]中定义的加权函数的相关性质，在此将不再赘述．对于ρ，υ∈U∞，S>0，f∈PCT(R，X)，定义

定理1令f∈PPAPT(Ω，X，ρ，υ)且h∈PPAPT(Ω，ρ，υ)．假设下面的条件成立：

(H2)f(t，·)对∀t∈R在每个有界子集Ω上是一致连续的，即对∀ε>0和有界集K⊂Ω，存在δ>0，使得当x，y∈K且‖x-y‖<δ时，‖f(t，x)-f(t，y)‖<ε对∀t∈R成立；

(H3)f(R，K)={f(t，x)：t∈R，x∈K}对每个有界子集K∈Ω是有界的．

若R(h)⊂K，那么f(t，h(t))∈PPAPT(X，ρ，υ)．

证因为f∈PPAPT(Ω，X，ρ，υ)，h∈PPAPT(Ω，ρ，υ)，所以f=fap+fe且h=hap+he．则函数f(·，h(·))可以做如下的分解：

由于R(hap)在X上是相对紧的，则∀t∈R，fap(t，·)在R(hap)上是一致连续的．由文献[11]的定理3.1，容易看出fap(·，hap(·))∈APT(R，X)．下面证明

令K∈Ω是有界的，使得R(h)，R(hap)⊂K．由条件(H3)，存在M>0使得

‖f(·，h(·))-f(·，hap(·))‖≤M∀t∈R

同时，由条件(H2)，对于ε>0，存在δ>0，使得当x，y∈K且‖x-y‖<δ时，有

其中

M(S，δ，he)={t∈[-S，S]： ‖he(t)‖≥δ}

又因为

‖h(t)-hap(t)‖=‖he(t)‖<δt∈QS/M(S，δ，he)

所以

由平移不变性可得，对S>S0，有

因为f=fap+fe，且当t∈R时，fap(t，·)在R(hap)上是一致连续的．那么由条件(H2)可知，fe(t，x)=f(t，x)-fap(t，x)关于t在x∈R(hap)上是一致连续的．即对于ε>0，存在δ>0，使得当x，y∈R(hap)且‖x-y‖<δ时，有

‖fe(t，x)-fe(t，y)‖<εt∈R

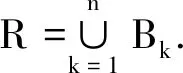
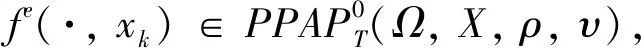
因此对于S>S0，有

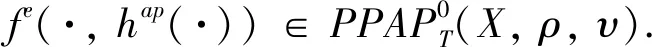
2 双加权伪概周期序列

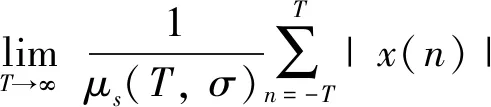
那么序列{x(n)}被称为σ，ϑ-PAP0序列，我们用PAP0S(X，σ，ϑ)来标记．

类似于文献[12]中引理2.1的证明，可以得到下面的引理：

引理1令σ，ϑ∈Vs∞．如果

定义

那么

类似于文献[12]中引理2.6和定理2.5的证明，容易得到下面的两个引理：

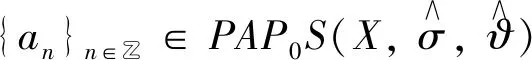
(H4) {Ii(u)：n∈Z，u∈K}在每个子集K⊆Ω上是有界的；

(H5) 当i∈Z时，Ii(u)在u∈Ω处一致连续．

那么

Ii(u(ti))=P1(i)+P2(i)i∈Z

注意到{u(ti)}和uap(ti)是有界的．令K⊂Ω是有界的，使得u(ti)，uap(ti)⊂K，i∈Z．由条件(H5)，对∀ε>0，存在δ1>0使得

由于K1是相对紧的，则存在x1，…，xm∈K1使得对每个i，有

‖uap(ti)-xk‖<δ1≤k≤m

此外，对于S>0，有

因此