级联失效下非对称依赖网络鲁棒性研究*
2021-02-01刘凤增刘俊杰王昊冉
刘凤增,肖 兵,刘俊杰,王昊冉
(1.空军预警学院 预警情报系,湖北 武汉 430019;2.国防科技大学 信息通信学院,湖北 武汉 430010;3.国防科技大学 系统工程学院,湖南 长沙 410073)
现代社会中,通信网、国际互联网、电网、交通网等网络化的信息物理系统与人们的生活息息相关[1]。这些信息物理系统通过相互依赖和协作发挥功能作用,单个系统中发生的故障可能引起其他系统故障,发生级联失效,严重时导致整个信息物理系统崩溃。例如2003年发生在意大利的大停电事故[2],首先是电力节点发生故障,依赖其供电的控制系统节点继而失效,控制系统节点失效导致无法进行正常调度,从而引发更多电力节点失效,级联失效不断传播,最终导致发生大规模停电。因此,具有依赖关系的信息物理系统安全性问题引起了广泛关注[3-4]。
2010年,Buldyrev等[5]在《Nature》杂志上发表文章,针对具有依赖关系的系统提出了相依网络级联失效模型,开启了相依网络鲁棒性研究的热潮。随后,学者们分别从子网类型、子网数量、相依模式、耦合强度等角度构建了多种相依网络模型,研究了相依网络在不同攻击方式下的鲁棒性问题[6-8]。其中,相依关系对相依网络的鲁棒性有着重要影响。Buldyrev[5]发现,在面对级联失效时,具有双向依赖关系的完全相依网络会发生一阶渗流相变,而在单个网络中是二阶相变,说明相依网络比单个网络更为脆弱。Parshani等[9]通过降低相依节点的比例,使渗流相变从一阶转换为二阶,从而提高了网络的鲁棒性。Zhong等[10]发现,在进行网络修复时,修复效果会随着相依节点比例上升而变差。Wang等[11]考虑依赖边两边节点的属性,提出同配相依、异配相依和随机相依等模式,发现同配相依的网络鲁棒性更强。Wang等[12]基于临近节点优先连接的原则提出了一种新的相依模式,在鲁棒性方面优于三种经典的相依模式。不同于上述固定相依模式,高彦丽等[13]提出了一种全局同质化的网络相依模式,可以动态地建立子网络之间的依赖边。通过研究相依节点间的对应关系,Shao等[14]发现多重相依关系使网络渗流相变从一阶转为二阶,显著增强了网络的鲁棒性。陈世明等[15]定义了相依冗余度来表示一个节点所拥有的相依节点数量,发现相依网络的鲁棒性随着相依冗余度的增加而增强。
上述工作深入地研究了相依关系对网络鲁棒性的影响,但大多数模型中的依赖关系为无向的。Fu等[16]研究了依赖边为有向的相依系统,由于存在较长的依赖链路,有向相依网络比无向相依网络的鲁棒性更差。在文献[16]的模型中,子网络间仍是相互依赖的关系。现实中有不少信息物理系统是单向依赖的。目前,学者们对这类系统的鲁棒性关注较少。因此,本文针对具有单向依赖关系的信息物理系统建立非对称依赖网络模型,通过调整子网参数和依赖关系可生成多种结构的实例网络。同时考虑网络结构和网络上的动力学过程,设计了包含相依失效和过载失效的级联失效模型。在随机攻击和蓄意攻击方式的基础上提出了一种非对称攻击方式,并设计了一种资源限制下的容量分配方式。通过仿真实验分析了子网结构、依赖模式、容量分配方式、攻击方式等因素与网络鲁棒性之间的关系,发现了影响网络鲁棒性的部分规律,总结了提高非对称依赖网络鲁棒性的方法。
1 双层非对称依赖网络模型
1.1 模型定义
现实中存在一类具有单向依赖关系的信息物理系统,如在作战体系中,指挥网依赖于通信网,而通信网一般不依赖于指挥网发挥功能。当一个通信节点失效,依赖其的指挥节点由于无法发送指挥信息而发生失效;当一个指挥节点失效,所依赖的通信节点并不会受到影响。针对这一类系统,将组分系统或网络抽象为子网络,将依赖关系抽象为子网间的单向依赖边,可基于相依网络理论定义非对称依赖网络模型如下:
定义1:当子网络A中的节点单向依赖于子网络B中的节点,且子网络B中的节点不依赖于子网络A中的节点,则称由子网络A和子网络B构成的相依网络为双层非对称依赖网络。
相应地,称子网络A为依赖子网,称子网络B为被依赖子网。子网络的内部边称为连接边(connectivity links),子网络间表示依赖关系的连边称为依赖边(dependency links)。一个节点拥有连接边的数量称为该节点的内部度,拥有依赖边的数量称为外部度。
模型示意如图1所示,可用图G=(V,E)表示,其中V=VA∪VB表示子网络A和子网络B中节点的并集;E=Econnectivity∪Edependency表示连接边和依赖边的集合。
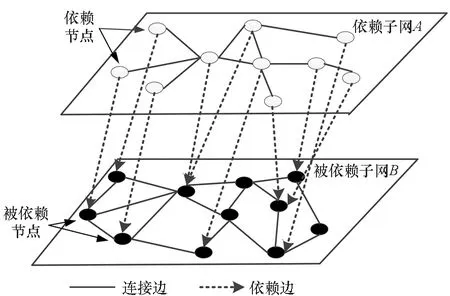
图1 双层非对称依赖网络模型Fig.1 Double-layer asymmetric network model
可用邻接矩阵W表示G:
(1)
式中:wij∈{0,1}表示节点间的连接关系;wij=wji=1表示节点vi和vj之间存在连边,且是无向的;wij=1,wji=0表示存在节点vi指向vj的有向边;wij=wji=0表示节点vi和vj之间不存在连边。WA表示子网络A的邻接矩阵,WB表示子网络B的邻接矩阵。WBA和WAB分别表示子网络A和子网络B的依赖关系。由于是单向依赖关系,WBA=0。当wij∈WAB且wij=1时,表示子网络A中的节点vi依赖于子网络B中的节点vj。
1.2 网络生成
为生成双层非对称依赖网络实例,在给定子网络规模NA和NB后,需选定子网络的类型和确定子网间的依赖关系。
1.2.1 子网类型
任意类型的网络都可作为子网络,现有研究中使用的模型网络主要有:随机网络(Erdös Rényi,ER)、随机规则网络(Random Regular,RR)、无标度网络(Scale Free,SF)、小世界网络(Watts-Strogatz,WS)等[11]。现实中一些复杂系统具有无标度特性[17],这里选用无标度网络模型生成子网A和子网B,利用Goh提出的可调参数无标度网络模型[18]进行生成。设初始网络中包含NA(NB)个孤立节点,给每个节点分别编号为1,2,…,NA,对第i个节点赋权重值为:
pi=i-θ
(2)
式中,0<θ≤1为控制参数。将权值归一化为:
(3)

(4)
可知γ≥2。因此通过调节θ和m可生成不同度指数和平均度的无标度网络。
1.2.2 依赖关系
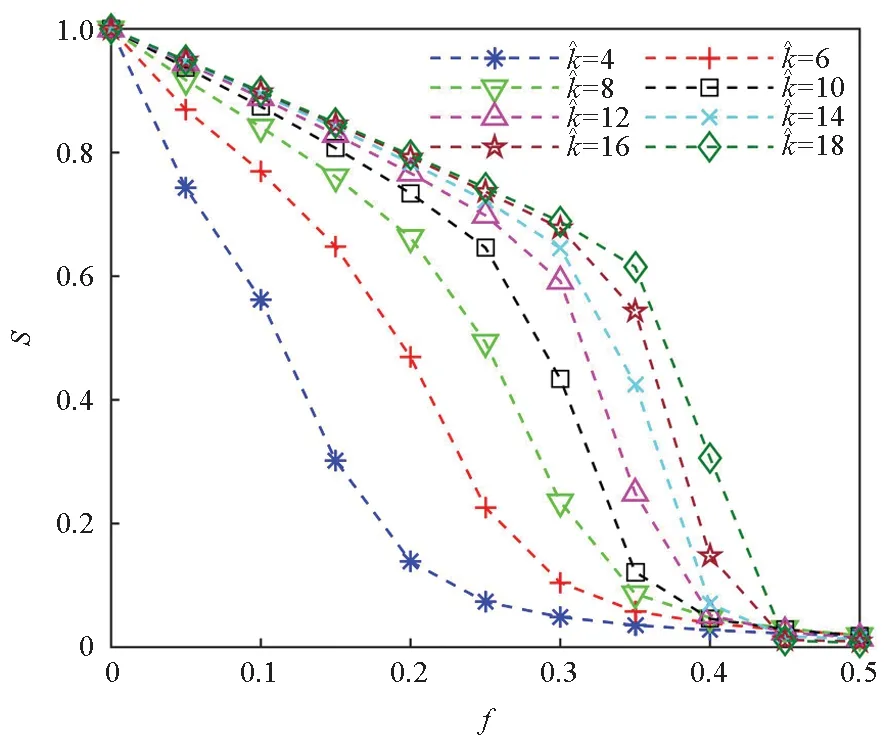
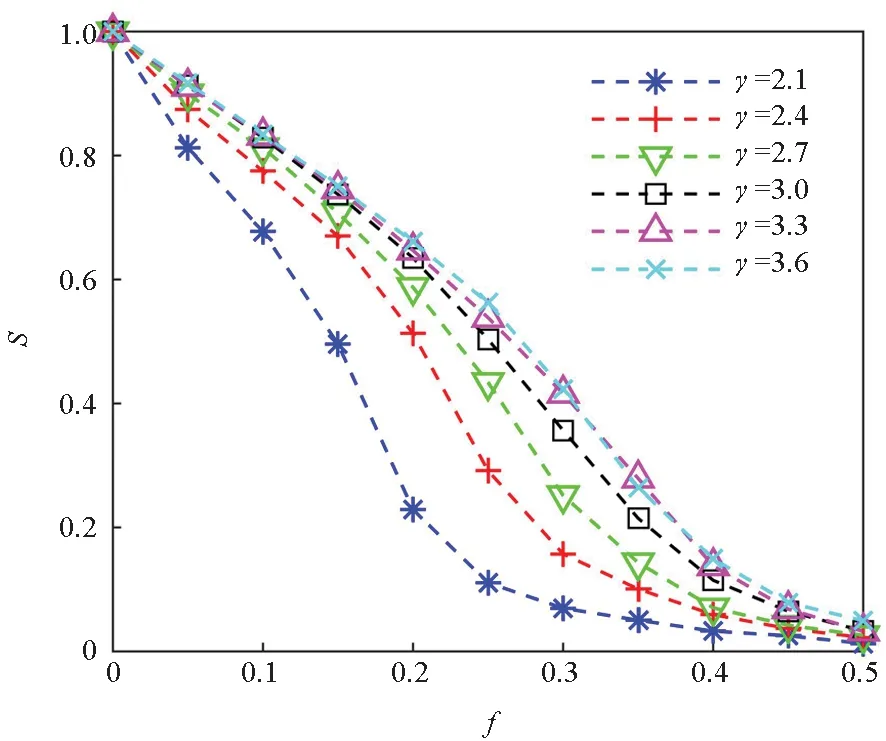
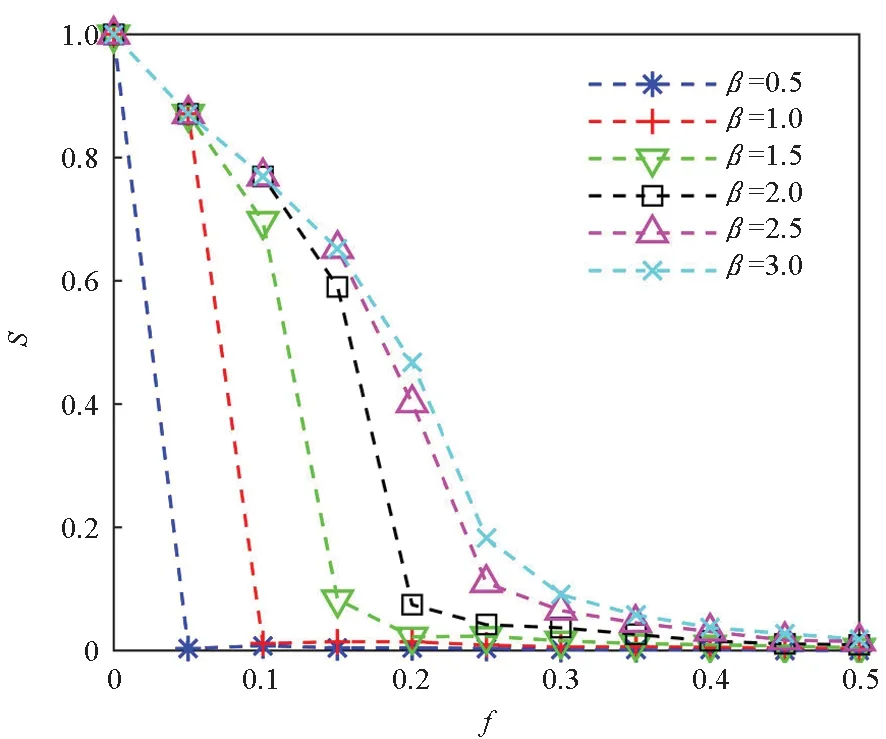
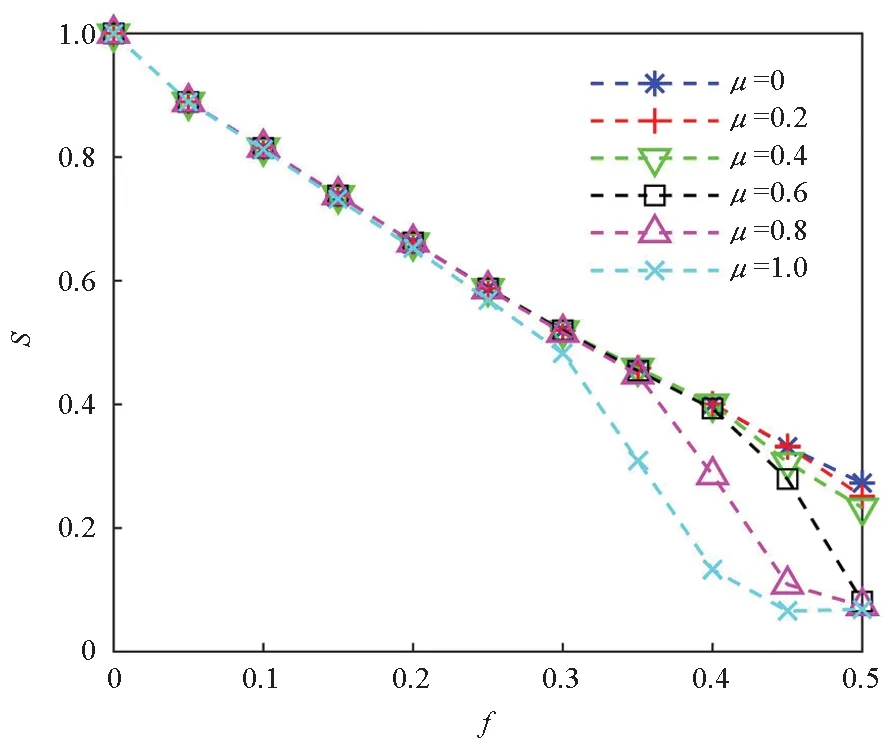
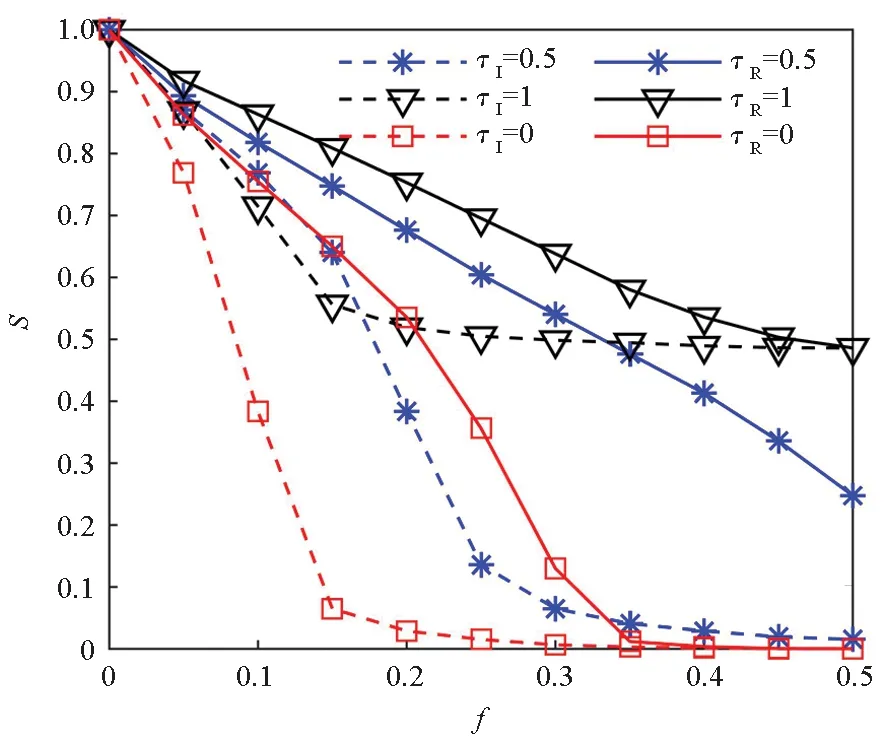
子网络A与子网络B的依赖关系包括依赖节点比例、对应关系和依赖模式。子网中依赖节点与该子网中节点总数的比例称为依赖节点比例,也有文献[19-20]称为耦合强度,用q表示。q=1时表示完全依赖,0 图2 三种依赖模式Fig.2 Three dependent modes 信息物理系统运行时可能会遭遇故障或攻击,一般用随机攻击和蓄意攻击来对攻击方式进行描述[20]。随机攻击是指不加区别地随机移除网络中的节点,蓄意攻击是指按照节点的重要度依次移除网络中的节点。衡量节点重要性的指标有度、介数、接近度、PageRank、特征向量等,这里使用度指标对节点进行排序[21]。已有研究大多是按照攻击方式等比例选择各子网节点进行移除。在现实中由于各子网的特性不同,遭受攻击时也存在不对称性。为描述这一情况,假设失效节点比例(又称攻击强度)为f,初始失效节点总数F=f(NA+NB)保持不变,子网A中的失效节点数为: FA=2τfNA (5) 子网B中的失效节点数为: FB=2(1-τ)fNB (6) 其中τ∈[0,1],用来调节各子网中初始失效节点的数量。τ=1表示仅攻击子网A中的节点;τ=0.5表示等比例攻击各子网中的节点;τ=0表示仅攻击子网B中的节点。用τI表示非对称蓄意攻击,初始阶段从子网络A和子网络B中分别选取排序靠前的FA和FB个节点进行移除;用τR表示非对称随机攻击,从子网络A和子网络B中分别随机选取FA和FB个节点进行移除。 依赖网络在遭受攻击后部分节点失效,引发其他节点失效,发生级联失效。结合文献[5]提出的相依失效模式,这里给定双层非对称依赖网络的依赖失效的规则:当节点不属于子网最大连通分支或者其依赖的全部节点发生失效时,则该节点发生失效。如图3所示,当子网B中的节点B1遭受攻击发生失效后,与节点B1相连的依赖边和连接边均被移除;在第二步,仅依赖于节点B1的节点A1和A3接着发生失效,节点B4因不再属于网络B中的最大连通分支而发生失效,失效节点的边均被移除;在第三步,节点A4和A6不再属于子网A的最大连通分支而发生失效;节点A2与节点B4的依赖边虽然被移除,但还存在与B3相连的另一条依赖边,因此节点A2不发生失效。当网络中没有满足失效规则的节点时,失效终止,网络进入稳定状态。 图3 双层非对称依赖网络依赖失效过程示意Fig.3 Cascading failure process of double-layer asymmetric network 依赖失效规则仅关注网络结构,而没有考虑网络上的负载,这与通信网等实际系统是不相符的。文献[22]结合容量-负载模型[23]定义了负载作用下的级联失效模型,在依赖失效的基础上增加了过载失效规则。在非对称依赖的信息物理系统中,并不是每个子系统上都存在过载失效,如位于信息域的指挥网很难发生过载现象,而位于物理域的通信网则可能由于流量过大发生过载失效。因此在双层非对称依赖网络模型中,假设仅在被依赖网络上存在过载失效。子网络B上过载失效的过程为:节点在初始正常工作状态下的负载为初始负载,当某一节点失效后,负载重分配到其他节点;其他节点获得负载后,如果总负载超过其容量,则导致该节点失效,引起新一轮的负载传播和节点失效。 2.3.1 容量-负载模型 (7) 式中,ki表示节点i的内部度,α是控制度对初始负载影响程度的参数。 在已有模型中,一般认为节点的容量Ci与初始负载呈正相关关系,定义为: (8) 式中,β是容忍系数。 当节点i失效后,其上的负载采取局部重分配的方式向邻居节点进行分配,邻居节点j获得的负载为: (9) 式中,Γi为节点i的邻居节点集合。获得负载后,节点j的总负载如果超过其容量,即 Lj+L′j>Cj (10) 此时,节点j发生过载失效。 2.3.2 容量分配方式 在实际信息物理系统中,增加节点的容量意味着花费成本和耗费资源。当成本一定时,能增加的节点容量也是一定的,此时如何分配容量成为提升网络鲁棒性的关键。假设在初始负载基础上增加的总容量为βL(L为初始总负载),则每个节点分配的冗余容量为: (11) 其中:μ为容量分配因子,当μ=0时,表示以节点初始负载为权重分配容量;当μ=1时,表示平均分配容量,即每个节点获得的新增容量是一样的;当0<μ<1时,表示上述两种方式的混合状态。 (12) 为消除随机因素的影响,一般按照同一生成规则产生M个网络进行仿真,得到一组留存节点比例s1,s2,…,sM,取其平均值: (13) 称S为平均留存节点比例。在遭遇攻击后,网络的S越大,说明网络的鲁棒性越好。 (14) 图4 不同子网络平均度下网络的鲁棒性Fig.4 Network robustness under different average degree of subnet 从图4可以看到,随着平均度提高,平均留存节点比例S也在不断增大,说明网络鲁棒性与子网络平均度呈正相关关系。从表1可发现,网络的鲁棒性增幅存在边际递减现象,即随着平均度的递增,网络的鲁棒性增幅逐渐变小。以上结果说明,通过提高子网络平均度可改善网络鲁棒性,在子网络平均度越低时改善效果越明显。 表1 不同子网络平均度下网络鲁棒性增幅Tab.1 Network robustness increase under different average degree of subnet 图5 不同子网络度指数下网络的鲁棒性Fig.5 Network robustness under different degree exponents of subnet 在子网络结构一致的基础上,针对同配依赖、异配依赖、随机依赖三种模式,分别生成网络并进行蓄意攻击和随机攻击实验。实验结果如图6所示,其中AD-IA和AD-RA表示分别对同配依赖网络进行蓄意和随机攻击;DD-IA和DD-RA表示分别对异配依赖网络进行蓄意和随机攻击;RD-IA和RD-RA表示分别对随机依赖网络进行蓄意和随机攻击。由图6可以看到,面对蓄意攻击且f<0.3时,同配依赖网络比异配依赖网络的S值略大,但明显比随机依赖网络的S值大;面对随机攻击且f>0.3时,同配依赖网络与随机依赖网络的S值差异较小,明显大于异配依赖网络的S值。这说明,不管面对哪种攻击方式,同配依赖网络的鲁棒性都是更好的。 图6 不同依赖模式下网络的鲁棒性Fig.6 Network robustness under different dependent modes 为考察节点容量对网络鲁棒性的影响,针对不同的容忍系数和容量分配因子进行网络毁伤实验。在默认实验参数的基础上,容忍系数β分别取0.5、1.0、1.5、2.0、2.5、3.0,实验结果如图7所示。 图7 不同容忍系数下网络的鲁棒性Fig.7 Network robustness under different tolerance coefficients 由图7可以看到,容忍系数对网络的鲁棒性影响比较大,当β=0.5时,移除5%的节点就可使整个网络崩溃;平均留存节点比例S随着容忍系数β的增大而提高,提升幅度随着容忍系数β的增大而呈现边际递减现象。这说明网络鲁棒性与节点容量呈正相关关系,在节点容量较小时,提高节点容量能够更有效地提升网络鲁棒性。 固定容忍系数为β=3,容量分配因子μ取0到1.0,分别进行网络蓄意攻击和随机攻击实验。在蓄意攻击实验中,针对各容量分配因子,平均留存节点比例S差异较小。在随机打击实验中,实验结果如图8所示,在初始损毁30%以下的节点时,平均留存节点比例S几乎没有差异;当f>0.3时,S随着容量分配因子μ的提高而减小。这说明按度值分配容量比平均分配容量方式更能提高网络抵御随机攻击的能力。 图8 不同容量分配因子下网络的鲁棒性Fig.8 Network robustness under different capacity allocation factors 为了分析非对称攻击方式对网络鲁棒性的影响,对生成的网络分别进行非对称蓄意攻击和非对称随机攻击实验。令τI的取值为0.5、1、0,分别表示同时蓄意攻击子网A和子网B、仅蓄意攻击子网A、仅蓄意攻击子网B;令τR的取值为0.5、1、0,分别表示同时随机攻击子网A和子网B、仅随机攻击子网A、仅随机攻击子网B。实验结果如图9所示,可以看到:蓄意攻击总是比随机攻击造成的损伤大;仅攻击子网B总是比仅攻击子网络A造成更大的毁伤。在蓄意攻击中,f≤0.15时,仅攻击子网A比同时攻击两子网的平均留存节点比例S更小,f≥0.2时情况则相反。在随机攻击时,仅攻击子网B可导致网络完全崩溃,而其他两种方式则不会。这说明,在攻击资源一定的情况下,仅攻击被依赖子网能够取得更大的攻击效果;在攻击资源较少(f≤0.15)时,仅蓄意攻击依赖子网也比同时攻击两子网的毁伤效果好。 图9 不同攻击方式下网络的鲁棒性Fig.9 Network robustness under different attack modes 信息物理系统中存在的级联失效现象可能使系统在遭受小部分节点毁伤后发生完全崩溃,研究发现影响系统鲁棒性的规律对于阻止系统崩溃具有重要意义。本文针对具有单向依赖关系的信息物理系统构建了双层非对称依赖网络模型,通过调整子网参数和依赖关系可生成不同结构的实例网络。同时考虑依赖失效和过载失效,设计了非对称依赖网络上的级联失效模型。为了更贴近实际情况,在随机攻击和蓄意攻击方式的基础上提出了非对称攻击方式,并给出了一种资源限制下的节点容量分配方式。仿真实验发现,通过提高子网的平均度和度指数、提高节点的容量等方式能够有效地改善网络的鲁棒性;同配依赖网络比异配依赖网络和随机依赖网络具有更高的鲁棒性;在总的容量增量不变的情况下,按度值分配比平均分配节点容量的网络鲁棒性更好;由无标度子网构成的非对称依赖网络面对蓄意攻击时具有脆弱性,在同样的攻击力度下,仅攻击被依赖子网时网络遭受的损伤更大,因此重要节点和被依赖子网络应得到更多的防护。实验结果对于设计更高鲁棒性的网络以及维护网络的正常运行具有一定的参考价值。 本文通过仿真实验发现了影响非对称依赖网络鲁棒性的部分规律,但还存在以下问题:生成的网络实例仅考虑了一对一完全依赖关系,没有考虑多重依赖、部分依赖、子网规模不对等的情况;实验中仅考察了单个因素对网络鲁棒性的影响,而没有考虑两个或多个因素的联合影响。这些将是下一步研究的重点。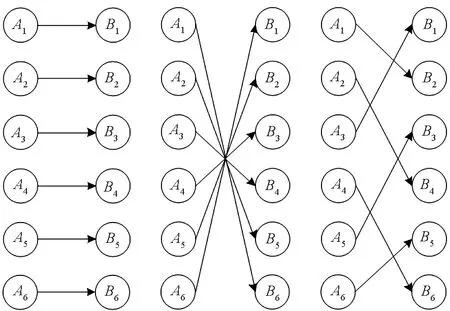
2 级联失效模型
2.1 攻击方式
2.2 依赖失效

2.3 过载失效
2.4 网络鲁棒性测度指标

3 仿真实验及结果分析

3.1 子网络结构对网络鲁棒性的影响

3.2 依赖模式对网络鲁棒性的影响

3.3 节点容量对网络鲁棒性的影响
3.4 攻击方式对网络鲁棒性的影响
4 结论
