改进Dijkstra算法在大型城市轨道交通网计价系统中的应用*
2021-02-01谢建平陈治亚邓连波谢宜斌
谢建平,陈治亚,邓连波,谢宜斌,杨 坤
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.长沙市轨道交通集团有限公司,湖南 长沙 410133)
随着城市地铁建设的迅猛发展,国内外众多城市地铁线路均已达到网络化运营规模。这将使得两个站点间存在多条行走路径,以哪条路径作为计价路径,才能确保其计价的科学性、合理性,是当前轨道交通行业研究的热点课题之一。
针对地铁两个站点间距离的长短对轨道交通计价的影响,国内外许多专家学者对此进行了深入的研究。文献[1]通过构建城市客运系统整体出行时间最小的双层规划模型,研究了城市轨道交通系统在城市客运结构中的作用。文献[2-6]通过建立模型对票价策略进行了优化,但未对轨道交通成网后各车站间票价计算方式进行深入探讨。文献[7-18]分别就节点约束型、改进的Dijkstra算法的最短路程计算,基于结合 Dijkstra算法的信息素递减蚁群( Dijkstra and Ant Colony Optimization based on Pheromone Declining,Dijkstra-PD-ACO)算法的大城市公交线路优化等方面进行研究和探讨,而对于Dijkstra算法优化,并将其应用于城市轨道交通各车站票价计算方面未做详细且深入的研究。文献[19-20]通过建立两种定价方式的双层规划模型对影响票价的因素进行研究,研究结果表明对价格的敏感度是影响两种定价的主要因素。
尽管有众多的专家学者针对Dijkstra算法在大型城市轨道交通线网计价系统中的应用进行了深入研究,但是到目前为止,对Dijkstra算法进行改进并将其应用在大型城市轨道交通线网计价系统中的研究很少。因此,对Dijkstra算法进行改进并将其应用在大型城市轨道交通线网计价系统中具有非常重要的意义。本文对传统的Dijkstra算法进行了改进,使用传统的Dijkstra算法和改进的Dijkstra算法计算分析了长沙地铁罐子岭站至毛竹塘站间的最短距离,并对结果进行了分析。为进一步研究Dijkstra算法在大型城市轨道交通线网计价系统中的应用提供了参考。
1 改进Dijkstra算法的实现
1.1 改进Dijkstra算法的主要思想
本算法主要根据地铁线网规划、建设规划、线路里程表等相关资料,提取线网各车站的里程标,绘制出地铁线网示意图,再筛选出线网所有换乘站,且对于同一线路中两换乘站之间无其他换乘站可认定为相邻换乘站。根据换乘站之间的关系及换乘站的中心线里程标,使用传统的Dijkstra算法计算各换乘站之间的最短距离。算法详细思路如图1所示。
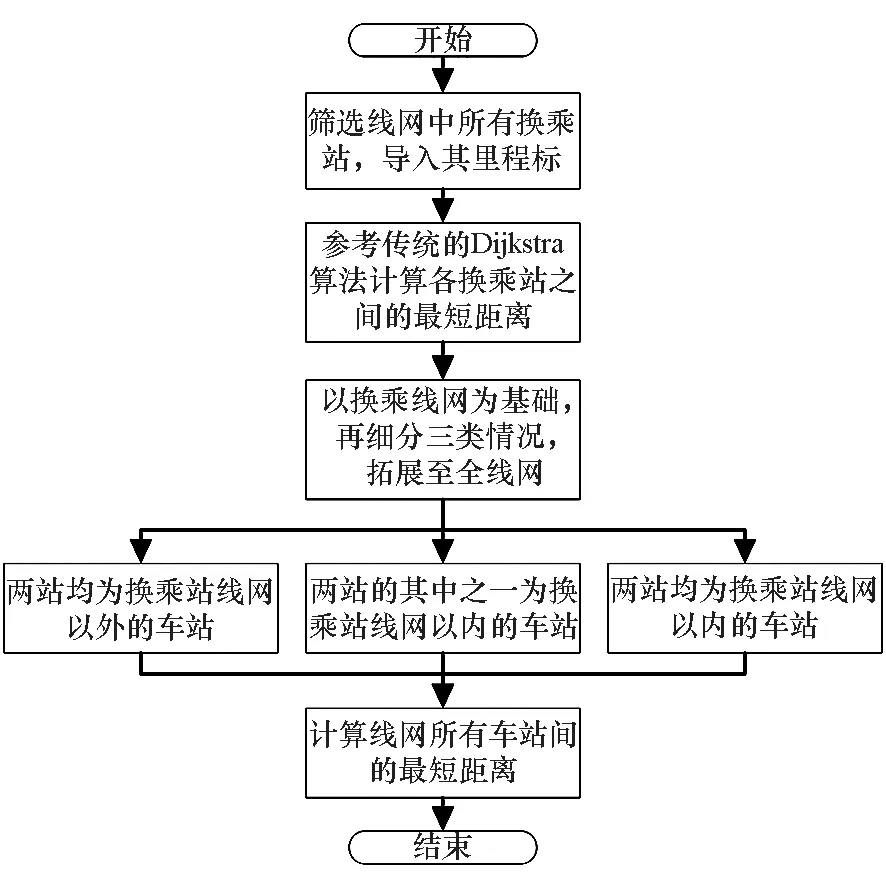
图1 改进Dijkstra算法流程图Fig.1 Improved Dijkstra algorithm flow chart
1.2 传统的Dijkstra算法计算换乘站间最短距离
假定地铁线网有n个换乘站,首先参照传统的Dijkstra算法计算出线网所有换乘站之间的最短距离,算法实现如图2所示。
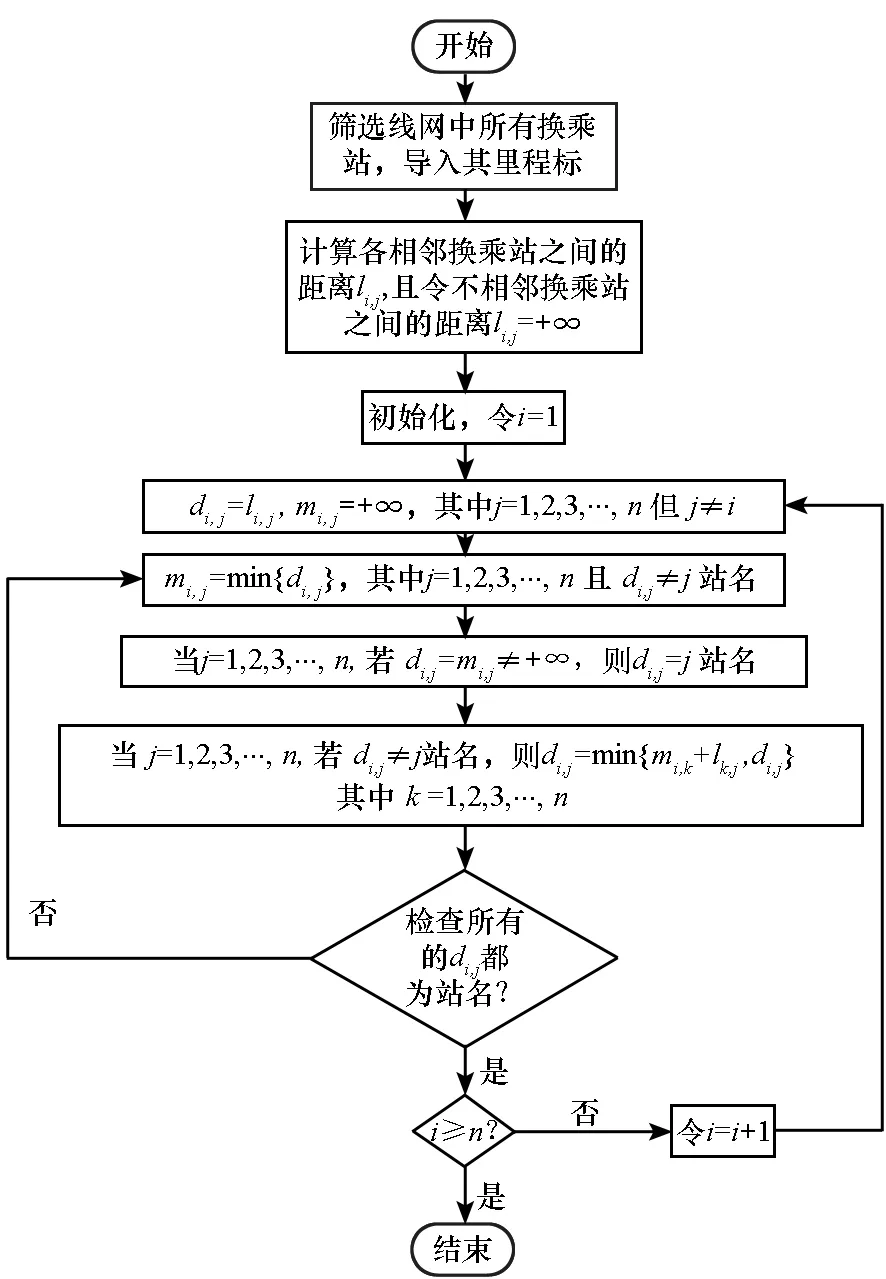
图2 传统的Dijkstra算法计算换乘站间最短距离流程图Fig.2 Traditional Dijkstra algorithm to calculate the shortest distance flow chart between transfer stations
算法详细描述如下:
Step1:筛选出线网中所有换乘站,导入其里程标。
Step2:计算所有相邻换乘站之间的距离li,j,令本站的li,i=0且不相邻换乘站之间的距离li,j=+∞,其中i=1,2,3,…,n。
Step3:初始化,令i=1。
Step4:初始化,令di,j=li,j,mi,j=+∞,其中j=1,2,3,…,n且j≠i。
Step5:比较所有新解且不为站名的di,j大小,即令mi,j=min{di,j},其中j=1,2,3,…,n且di,j≠j站名。
Step6:对于所有j=1,2,3,…,n,当di,j=mi,j≠+∞时,则令di,j=j站名。
Step7:对于所有j=1,2,3,…,n,若di,j≠j站名,则令di,j=min{mi,k+lk,j,di,j},其中k=1,2,3,…,n。
Step8:检查是否所有j的di,j=j站名,其中j=1,2,3,…,n,若为否,则跳至Step 5,若为是,则跳至下一步。
Step9:检查i是否大于等于n,若为否,则令i=i+1且跳至Step 4,若为是,则该算法结束。
其中:i,j表示换乘站线网中第i或j个换乘站;n表示换乘站线网总计有n个换乘站;li,j表示两相邻换乘站i和j之间的距离,若不相邻,其取值为+∞;mi,j表示换乘站i与换乘站j之间的最短距离;di,j表示换乘站i与换乘站j之间的最短距离求值过程中经历的中间值。
1.3 改进的Dijkstra算法计算线网各车站间最短距离
参考如上算法,计算出各换乘站之间最短距离表,再参考图2流程图中算法的主要思想,细分三个部分对线路各车站间最短距离进行计算,其具体的算法实现如图3所示。
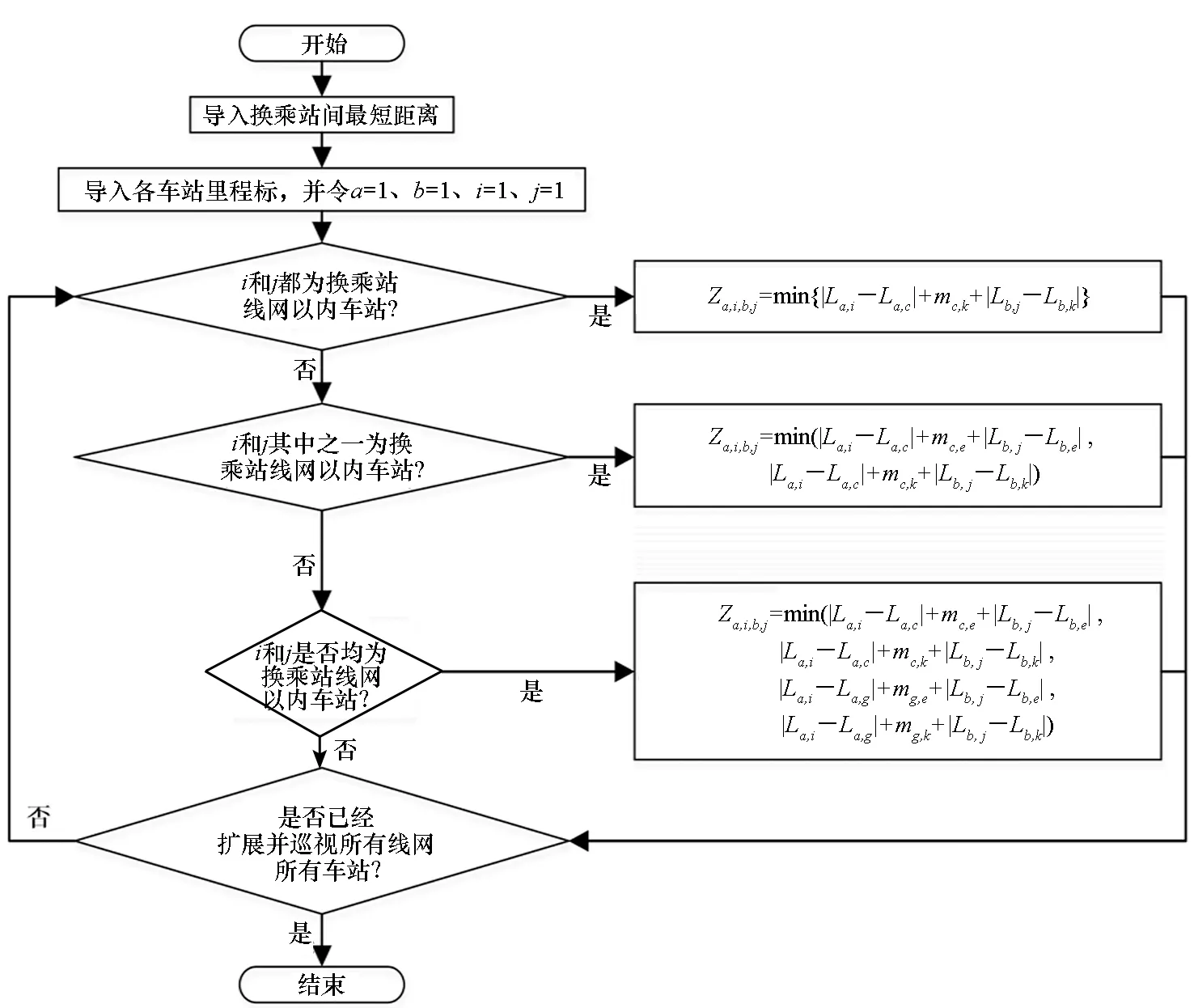
图3 改进的Dijkstra算法计算换乘站间最短距离流程图Fig.3 Flow chart which used the improved Dijkstra algorithm to calculate the shortest distance between the stations
算法详细描述如下:
Step1:导入换乘站间的最短距离即图2算法的结果,并参考换乘站在线网中的实际位置对算法结果进行适当的调整。
Step2:导入线网中各车站的线路里程标,并令a=1、b=1、i=1、j=1。
Step3:检查i和j是否为换乘站线网以内的车站,若为否,则跳至下一步,若为是,则令:
Za,i,b,j=min{|La,i-La,c|+mc,k+|Lb,j-Lb,k|}
(1)
Step4:检查i和j其中之一是否为换乘站线网以内的车站,若为否,则跳至下一步,若为是,则令:
Za,i,b,j=min(|La,i-La,c|+mc,e+|Lb,j-Lb,e|,
|La,i-La,c|+mc,k+|Lb,j-Lb,k|)
(2)
Step5:检查i和j是否均为换乘站线网以内的车站,若为否,则跳至下一步,若为是,则令:
Za,i,b,j=min(|La,i-La,c|+mc,e+|Lb,j-Lb,e|,
|La,i-La,c|+mc,k+|Lb,j-Lb,k|,
|La,i-La,g|+mg,e+|Lb,j-Lb,e|,
|La,i-La,g|+mg,k+|Lb,j-Lb,k|)
(3)
Step6:判断是否已经扩展并巡视所有线网所有车站,若为否,则跳至Step 3,若为是,则该算法结束。
其中:a、b表示线路编号,当算法巡视所有车站时,a和b均等于线路总数;i表示第a条线路中第i个车站,i不大于第a条线路车站总数;j表示第b条线路中第j个车站,j不大于第b条线路车站总数;La,i表示线路a中第i个车站的中心线里程标;Lb,j表示线路b中第j个车站的中心线里程标;Za,i,b,j表示第a条线路中第i个车站与第b条线路中第j个车站的最短距离;c、g表示为图3中离线路a第i个车站最近的换乘站,是线路a上的第c和g个车站;e、k表示为图3中离线路b第j个车站最近的换乘站,是线路b上的第e和k个车站;mc,e、mc,k表示换乘站c与换乘站e或k的最短距离,是根据图2算法求出的结果。
1.4 线网各车站间票价计算算法
根据图3中算法求出线网各车站之间最短距离Za,i,b,j,再参考如图4所示算法,核算线网各车站之间的票价。
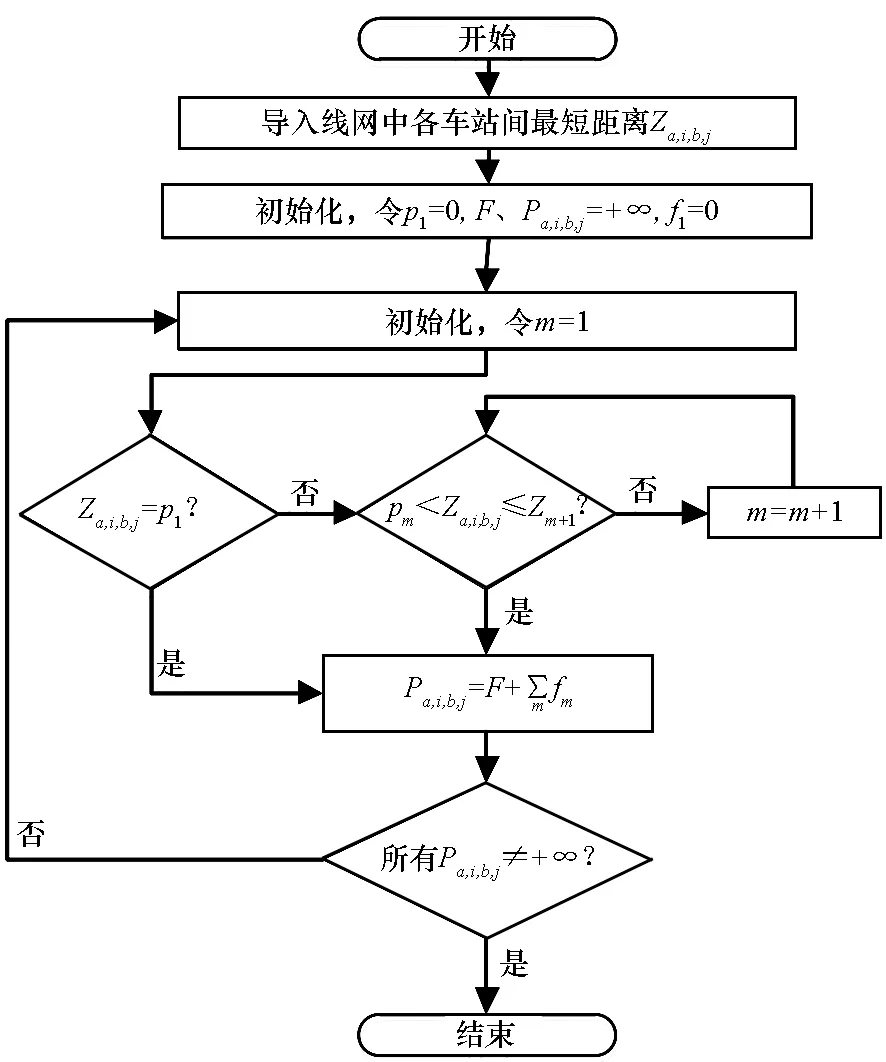
图4 线网各车站间票价计算算法Fig.4 Algorithm flow chart of ticket price between stations in line network
算法详细描述如下:
Step1:导入线网各车站间最短距离Za,i,b,j,即图3的计算结果。
Step2:初始化,令p1=0,F、Pa,i,b,j均为+∞,f1=0。
Step3:初始化,令m=1。
Step4:判断第a条线路第i个车站与第b条线路第j个车站之间的最短距离Za,i,b,j是否等于p1,即Za,i,b,j=p1,若为是,则跳至Step 6,若为否,则跳至Step 5。
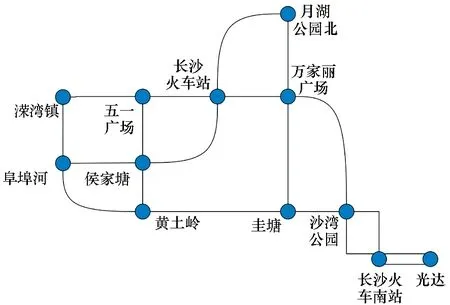
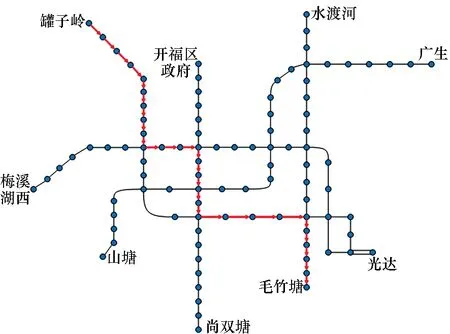
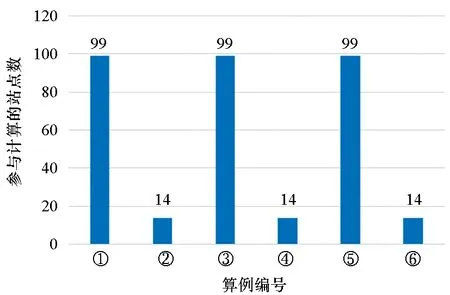
Step5:判断第a条线路第i个车站与第b条线路第j个车站之间的最短距离Za,i,b,j属于哪个计价区间,即检查pm Step7:检查所有Pa,i,b,j是否不等于+∞,即Pa,i,b,j≠+∞,若为否,则跳至Step 3,若为是,则该算法结束。 其中:m表示城市地铁第m个计价区间;pm表示在第m个计价区间乘客可乘坐的距离,F表示城市地铁起步票价;Pa,i,b,j表示第a条线路中第i个车站与第b条线路中第j个车站的票价,fm表示第m个计价区间较第m-1个计价区间需要调整的票价。 以长沙地铁罐子岭站至毛竹塘站、罐子岭站至赤岗岭站、湖南师大站至赤岗岭站的最短距离计算为例。对于传统算法需要根据长沙地铁1~5号线线网布局及各车站的中心线里程标,计算线网中各相邻车站之间的距离,以罐子岭站(或湖南师大站)为目标节点,并建立集合1,开始遍历长沙地铁1~5号线线网各车站,逐步将计算出最短距离的车站纳入集合1,算法在完成长沙地铁线网99个车站间最短距离的计算后结束,并根据要求提取出罐子岭站至毛竹塘站(或罐子岭站至赤岗岭站,或湖南师大站至赤岗岭站)的最短距离。改进的Dijkstra算法需根据长沙地铁1~5号线线网布局及各车站里程标,将线路中换乘站筛选出来,根据长沙地铁1~5号线线网布局,共计有12个换乘站,若任意两个换乘站在同一线路且其之间无其他换乘站,则认定其为相邻换乘站,将相邻换乘站连接起来,形成换乘站线网(如图5所示),并计算相邻换乘站之间的距离;再根据传统Dijkstra算法,计算各换乘站之间最短距离,而长沙地铁的换乘站线网图只有12个换乘站,较线网99个车站,计算难度及消耗时间大大缩减;再详细按照图3将线网各车站细分为三类,计算罐子岭站至毛竹塘站、罐子岭站至赤岗岭站,湖南师大站至赤岗岭站的最短距离,如罐子岭站和毛竹塘站均为换乘站线网以外的车站,则罐子岭站至毛竹塘站的计算方法可参考图3中第一种情况,对于罐子岭站至赤岗岭站而言,其中赤岗岭站为换乘站线网以内车站,则罐子岭站至赤岗岭站的计算方法可参考图3中第二种情况,湖南师大站和赤岗岭站均为换乘站线网以内车站,则湖南师大站至赤岗岭站的计算方法可参考图3中第三种情况。图6和图7以罐子岭站至毛竹塘站为例,使用两种算法时所涉及的站点及最短距离行走路径标记如下所示。 图5 长沙地铁1~5号线换乘站线网图Fig.5 Transfer station network of Changsha metro line 1~5 图6 传统Dijkstra算法计算罐子岭站至毛竹塘站最短距离时行走路径Fig.6 Traditional Dijkstra algorithm to calculate the shortest walking path between Guanziling station and Maozhutang station 由图6和图7可知,使用传统Dijkstra算法计算罐子岭站至毛竹塘站间最短距离时,参与计算的站点数为99,使用改进的Dijkstra算法计算罐子岭站至毛竹塘站间最短距离时,参与计算的站点数为14。具体情况如表1和图8~10所示,图中①~⑥与表1中标号相对应。 图7 改进Dijkstra算法计算罐子岭站至毛竹塘站最短距离时行走路径Fig.7 Improved Dijkstra algorithm to calculate the shortest walking path between Guanziling station and Maozhutang station 图8 参与计算的站点数比较图Fig.8 Comparison chart of the number of stations participating in calculation 由表1可知,传统Dijkstra算法与改进的Dijkstra算法的行走路径和最短距离大致相同,但在参与计算的站点数、计算次数、数据存储及运行时间方面,改进的Dijkstra算法都进行了大量缩减。 表1 传统Dijkstra算法和改进Dijkstra算法的算例比较Tab.1 Example compared with traditional Dijkstra algorithm and improved Dijkstra algorithm 注:目前长沙地铁票价政策是“起步价2元可乘坐6 km(含6 km),超过6 km采用‘递远递减’的计价原则,6~16 km(含16 km)范围每递增5 km加1元,16~30 km(含30 km)范围内每递增7 km加1元,30 km以上每递增9 km加1元”,参考表1可知,罐子岭站至毛竹塘站的最短距离为31.349 km,属于30 km以上范围,票价为7元,罐子岭站至赤岗岭站的最短距离为21.673 km,属于16~23 km(含23 km)范围,票价为5元,湖南师大站至赤岗岭站的最短距离为8.607 km,属于6~11 km(含11 km)范围,票价为3元。 图9 计算次数比较图Fig.9 Comparison chart of calculation times 图10 数据存储比较图Fig.10 Data storage comparison chart 当使用传统Dijkstra算法和改进的Dijkstra算法求任意两车站之间最短距离时,所需参与计算的站点数、计算次数及数据存储比较如表2所示。 表2 传统Dijkstra算法和改进Dijkstra算法比较Tab.2 Comparison between original Dijkstra algorithm and improved Dijkstra algorithm 表2中,S为地铁线网站点总数;n为地铁线网中换乘站总数;x为已经寻找出最短路径的站点,初始值为1;t为固定参数值,当两车站均为换乘站线网(含换乘站)以外车站时t取1,其中之一为换乘站线网以内车站时t取3,两个均为换乘站线网(含换乘站)以内车站时t取5。 在计算过程中,使用传统Dijkstra算法计算某两个站点的最短距离时,就需要先根据里程表计算各站点之间的距离初始值,相邻站点之间的距离为|La,i-La,i+1|,非相邻车站之间的距离为+∞,其计算次数为S2。而改进的算法中,需要先筛选相应换乘站,并根据换乘站之间的关系,求出各换乘站之间的距离初始值,其计算次数为n2。 在计算过程中,传统的Dijkstra算法需要的第一个数组,大小为S2,存储所有车站的初始距离值,并可以用来存储计算中间值;第一个数组,大小为S,存储起点至所有车站的最短距离;第三个数组,大小为S,存储所有节点里程标。而改进的Dijkstra算法,需要存储的换乘站数组及参与计算车站里程表的数组总数为n2+2n+2,此外,还需要一个变量存储起点至要求节点的最短距离。 以长沙地铁1号线北延线一期为例,假定La,i表示线路a中第i个车站的中心线里程标,Lb,j表示线路b中第j个车站的中心线里程标,使用改进Dijkstra算法求解如下: Step1:当i,j均为1号线北延线一期车站,则最短距离Z1,i,1,j=|L1,i-L1,j|。 Step2:当i或j之一为1号线北延线一期车站,假定i为1号线北延线一期车站,则最短距离Z1,i,b,j=|L1,i-L1,1|+Z1,1,b,j,由于i车站为1号线北延线一期车站,离其最近的车站为1号线第1个车站。 Step3:当i和j均非1号线北延线一期车站,则最短距离Za,i,b,j=Za,i,b,j。 算法实例如表3所示。 表3 改进的Dijkstra算法的延展性算例Tab.3 Example of extension of improved Dijkstra algorithm 由于长沙地铁1号线北延线为1号线新增车站,若按照传统的Dijkstra算法的原理计算线网中所有车站(含新增车站)间最短距离,需遍历线网所有车站进行求解,计算烦琐性增加,显然其延展性较改进的Dijkstra算法差。 1)改进后的Dijkstra算法克服了传统算法时间冗长的缺陷,创新地将换乘站从线网中独立出来,再通过换乘站线网拓展至线网各站,实际中,换乘站数量远远小于线网车站总数,这就减少了节点遍历数和查询时间,增强了设计的可行性; 2)若需知道线网各车站间最短距离,无须逐一核算各相邻车站之间的距离,减少了产生误差的可能性; 3)在换乘站不变,但有新线开通时,只需将车站里程标导入,便可直接计算出该站至其他车站的最短距离,可延展性更强。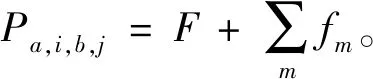
2 改进Dijkstra算法实例与分析
2.1 算法实例


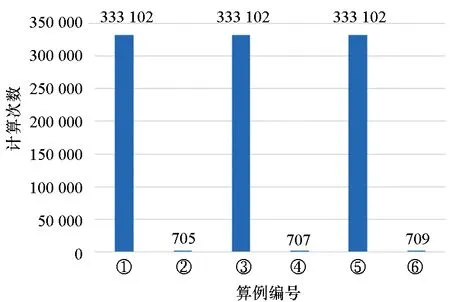
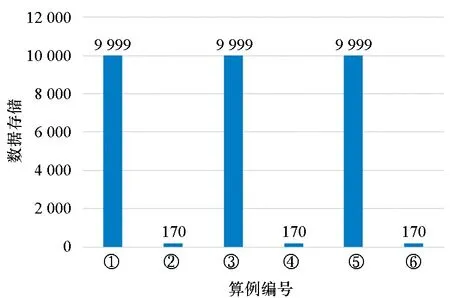
2.2 比较分析

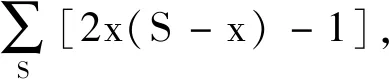
2.3 算法延展

3 结论
