复杂建筑结构环境下冲击波超压的快速估算方法
2021-02-01陈鑫高轩能付诗琦
陈鑫, 高轩能, 付诗琦
(1. 华侨大学 土木工程学院, 福建 厦门 361021; 2. 福建农林大学 交通与土木工程学院, 福建 福州 350002)
爆炸荷载的破坏力巨大,快速评估爆炸袭击或意外爆炸对建筑结构及人员安全的影响具有重要的意义.以往的研究已经总结了无约束环境下的爆炸冲击波超压的经验公式,但当在城市街区中或大型结构内等复杂三维环境下发生爆炸时,爆炸点高度、地面刚度、地面成坑情况、建筑表面形状、墙面和窗户的刚度和破损程度等诸多不确定因素都使爆炸荷载变得极为复杂,经验公式无法适用.因此,必须寻求一种在复杂建筑结构环境下,爆炸冲击波超压荷载分布的快速计算方法.
杨亚东等[1]以结构壁面作为镜面,把反射波按镜像爆炸源的入射波计算,并叠加各壁面的镜像入射波,快速获得了长方体房间内的内爆炸冲击波.但这一计算方法必须将壁面假设为刚性,且适用于较为简单的几何空间区域.另外,由于进行足尺模型爆炸试验的成本昂贵,而缩尺模型试验受到材料的高应变率效应的影响,存在不完全相似关系,与实际情况存在偏差[2].因此,采用数值方法建立流固耦合模型模拟,是目前分析复杂环境内超压荷载分布的主要手段.
为了获得较高的计算精度,流固耦合模型需要大量精细的任意拉格朗日欧拉(ALE)网格[3],计算成本高.LS-DYNA有限元软件提供的ALE与LBE相结合的方法[4-5],以及AUTODYN软件提供的重映射(REMAP)技术[6],都是将爆炸荷载分成简单自由场传播和流固耦合两阶段计算,节约了计算成本.这两种方法适用于爆炸源周围空旷无干扰,需要流固耦合分析的目标区域小的情况,若要对较大的耦合场进行分析时,依然需要大量的ALE网格.鉴于降低计算成本和提高计算精度的矛盾,本文提出采用粗网格进行低成本的流固耦合模拟,初步获得爆炸荷载场,再利用基于经验公式拟合的修正公式进行修正,获得精度较高的超压估算方法.
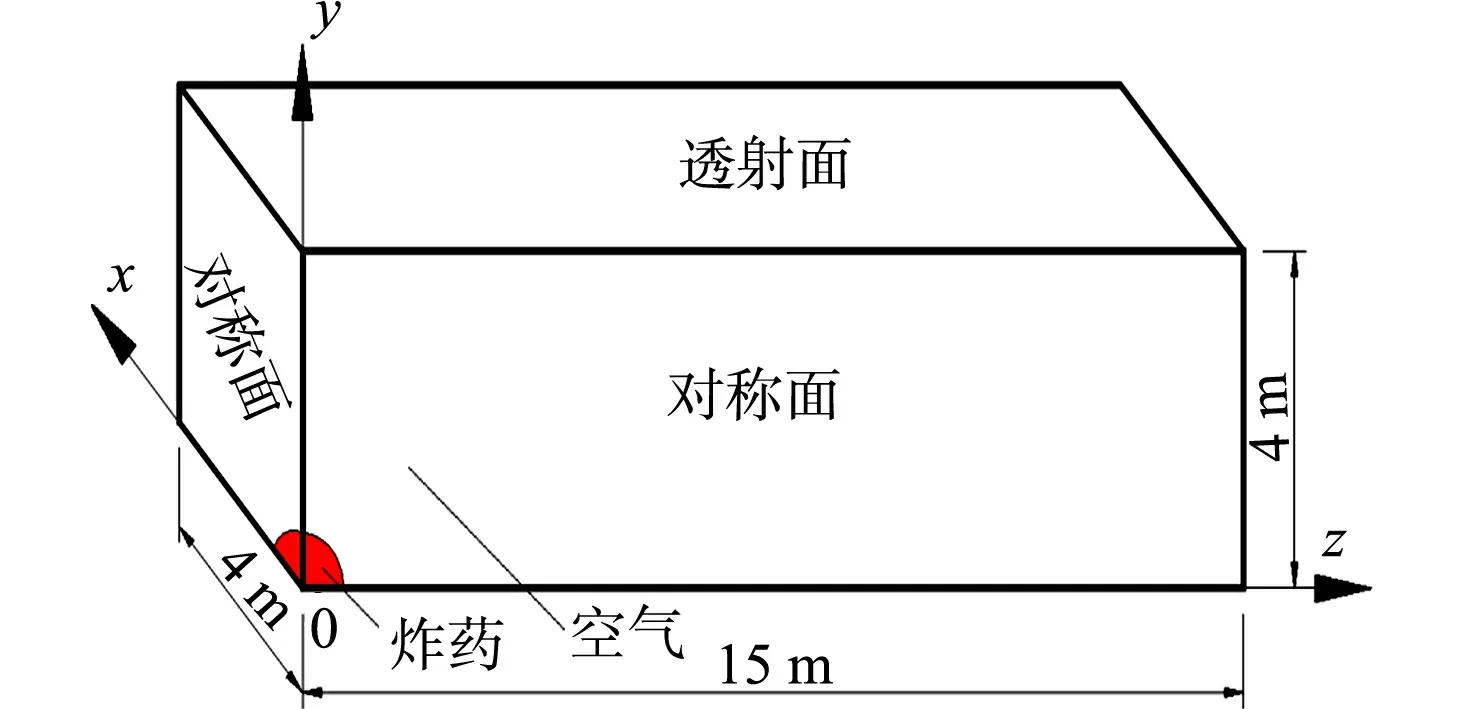
图1 自由场空爆模型Fig.1 Model of free-field explosion
1 有限元模型与材料参数
估算方法的核心在于拟合出超压修正公式,为确定超压修正公式的适用范围,利用LS-DYNA有限元软件,建立自由场空爆ALE模型,根据对称性建立1/8模型.模型的计算空间尺寸为4 m×4 m×15 m(长×宽×高)的空气域,如图1所示.利用“体积分数”语句在空气域中分割一个球形的区域,用以填充炸药材料.在模型的3个对称面上施加对称约束,其余表面均采用透射边界以模拟无限空气域.
炸药选用*MAT_HIGH_EXPLOSIVE_BURN材料模型,并用Jones-Wilkins-Lee状态方程描述爆炸物的特性,表达式为
(1)
式(1)中:P为压力;V为体积;A,B,R1,R2,ω为状态方程参数,通过试验确定参数的取值;E0为炸药的单位体积初始内能.炸药的材料参数[7],如表1所示.表1中:v为爆速;PCJ为爆压.炸药密度ρ取1 630 kg·m-3.

表1 炸药的材料参数Tab.1 Material parameters of explosive
空气选用*MAT_NULL材料模型,方程选用*EOS_LINEAR_POLYNOMIAL,即
P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)Ea.
(2)
式(2)中:μ=ρa/ρa0-1,ρa0为空气的参考质量密度,ρa为空气密度,取1.290 kg·m-3;单位体积内能Ea取2.5×105J·m-3;实常数C0=C1=C2=C3=C6=0,C4=C5=0.4.
2 超压误差和网格尺寸经济性分析
利用节1中自由场空爆模型对超压模拟误差进行分析,并进一步定义网格尺寸的粗细程度.为了便于分析,引入网格密度λ,即
λ=r/b.
(3)
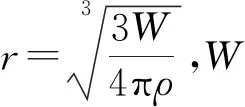
2.1 冲击波超压的误差分析
取b=0.05 m,W=100 kg进行计算,易得炸药半径r=0.245 m,网格密度λ=4.90.将文中模拟得到的爆炸冲击波超压峰值ΔPM与文献[8-11]中的入射超压经验公式计算值进行对比,结果如表2所示.表2中:ΔPH为根据Henrych等[8]的试验公式计算出的超压值,有
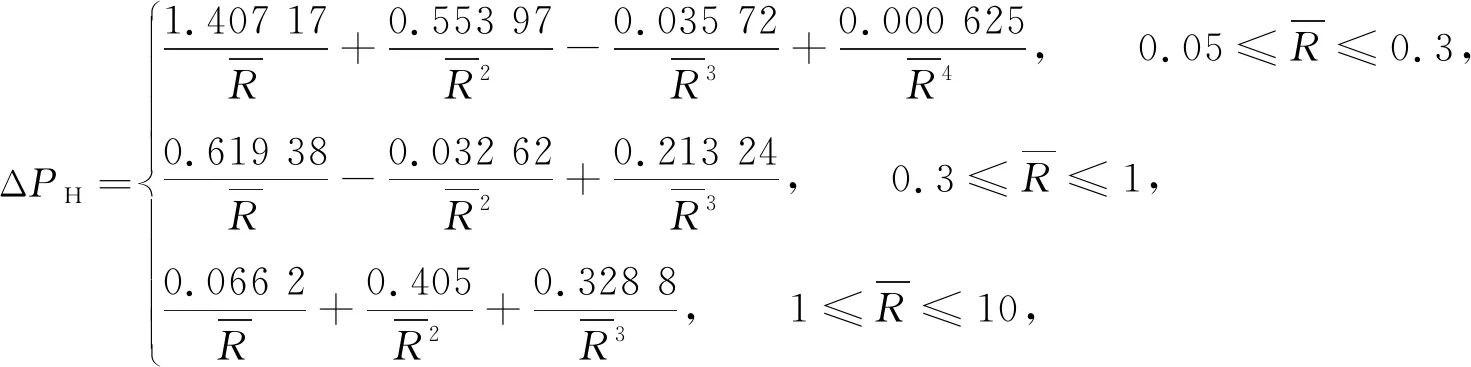
(4)
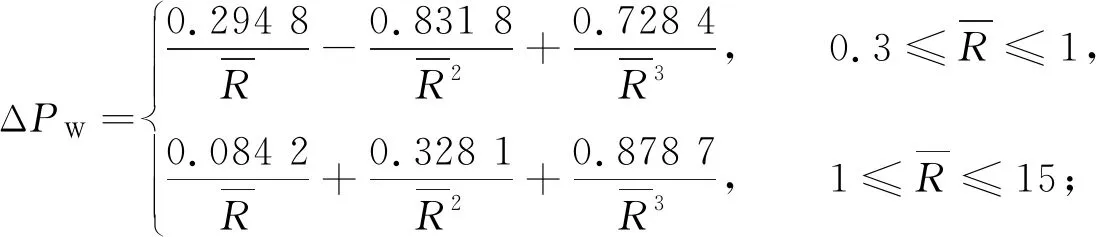
(5)
ΔPY为杨涛春等[10]统计18组入射波超压公式获得的回归公式计算值;ΔPB为根据GB 6722—2014《爆破安全规程》[11]公式计算的超压值.
由表2可知:在4组经验公式中,ΔPH的数值最小,且与ΔPM最为接近,ΔPW最为保守.

表2 文中模拟值与经验公式计算值的对比Tab.2 Comparison of overpressure values by numerical simulation and empirical formula
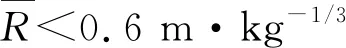
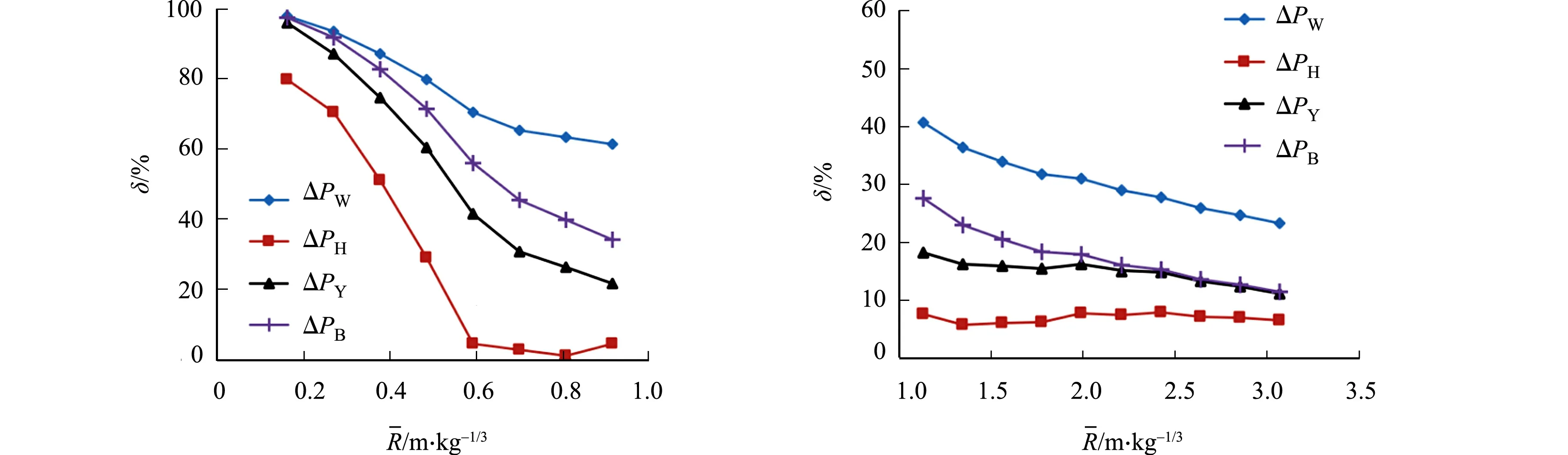
图2 比例距离与超压模拟误差曲线(λ=4.90)Fig.2 Curves of scale distance and overpressure simulation error (λ=4.90)
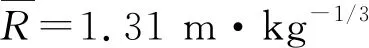
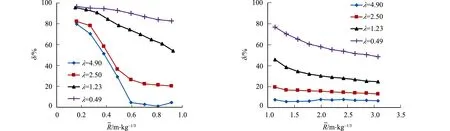
图3 网格密度对超压模拟误差的影响Fig.3 Influence of mesh density on overpressure simulation error
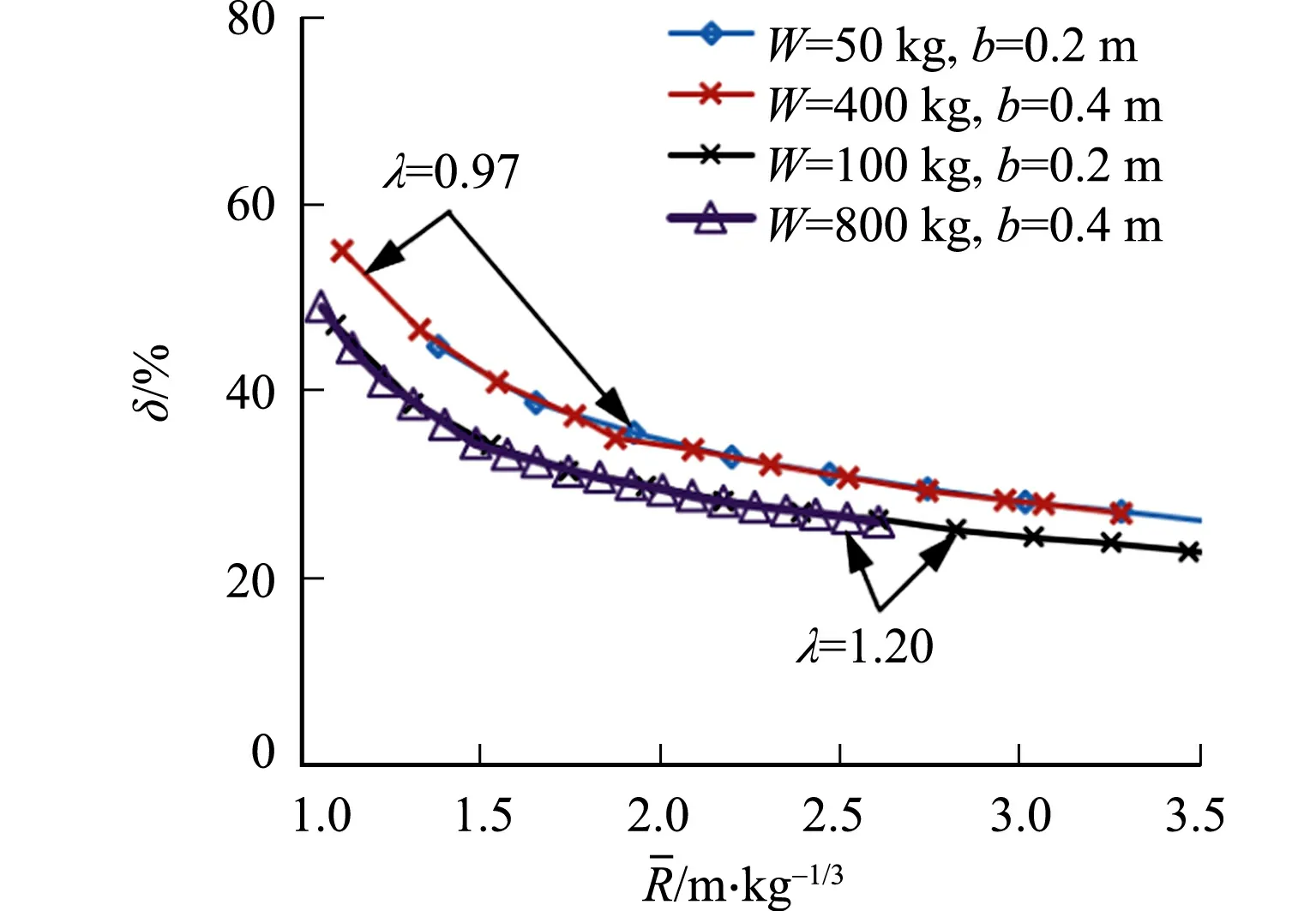
图4 炸药质量对超压模拟误差的影响Fig.4 Influence of explosive weight on overpressure simulation error
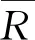
对于相同的网格尺寸,炸药质量W的变化会改变网格密度λ,从而影响超压误差δ.分析炸药质量W对δ的影响,结果如图4所示.由图4可知:不同炸药质量下,相同网格密度的超压误差曲线基本重合,说明只要保证相同的网格密度,可以忽略炸药质量对超压误差的影响.
2.2 网格尺寸经济性分析
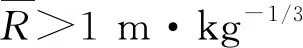
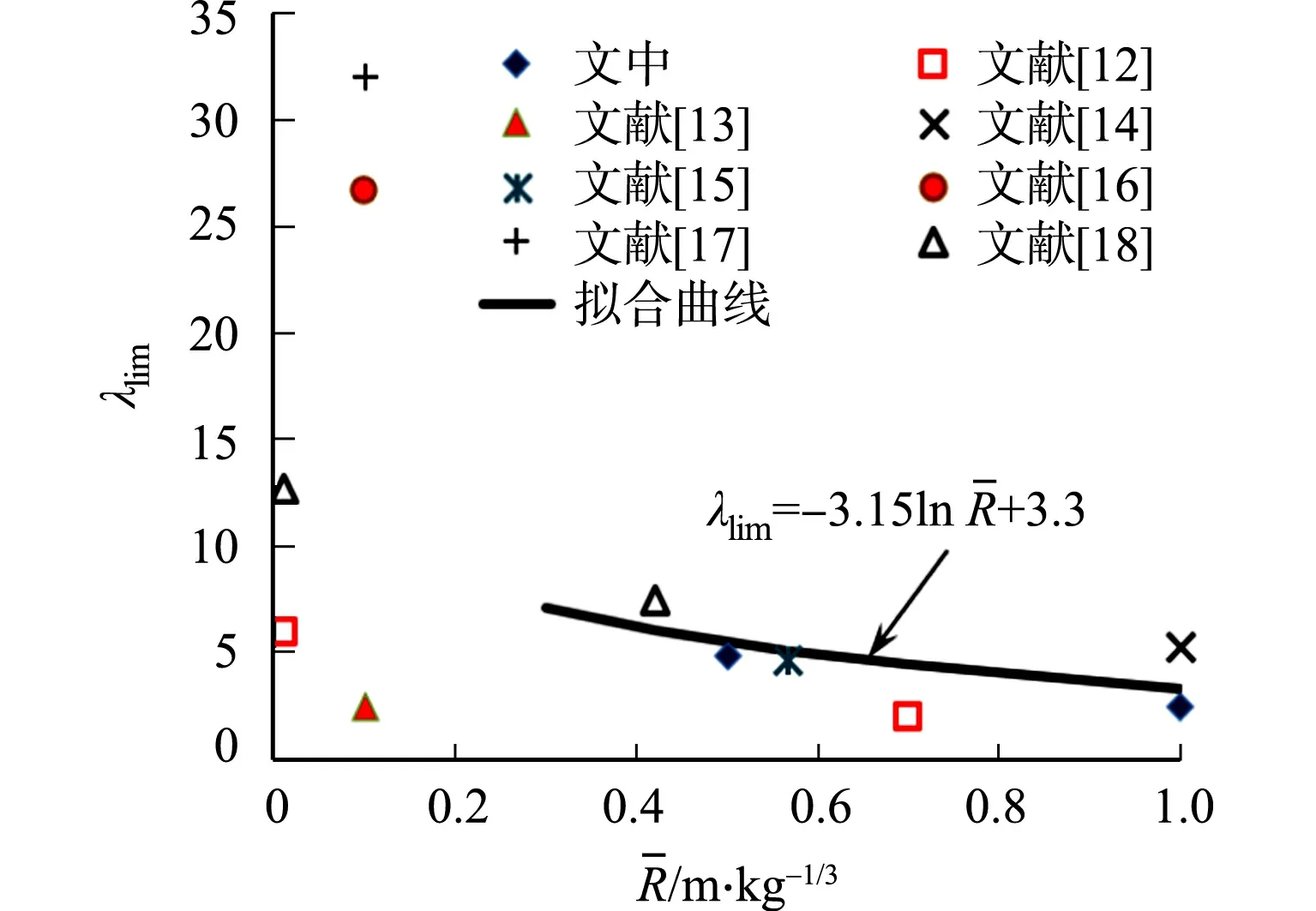
图5 网格密度限值与比例距离的拟合曲线Fig.5 Fitting curve of mesh density limit and scale distance
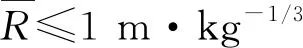
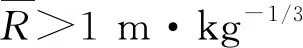
(6)
由此,定义λ<λlim的网格尺寸为粗网格;反之,则为细网格.采用细网格对3D环境进行模拟,所需要的单元数量十分巨大.以装药量860 kg的“飞毛腿B”导弹为例,杀伤半径达到150 m.若建立尺寸为300 m×300 m×150 m(长×宽×高)的爆炸区域,采用由λlim计算的0.2 m细网格,至少需要16.875亿个单元,还未计入城市建筑模型的单元数量.由于细网格的计算成本极高,在计算资源有限的情况下,可以采用粗网格模拟计算,并通过修正获得更精确的冲击波超压.
3 冲击波超压的快速估算
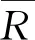
(7)
式(7)中:D1,D2和D3均为无量纲的拟合系数.
3.1 修正系数式1
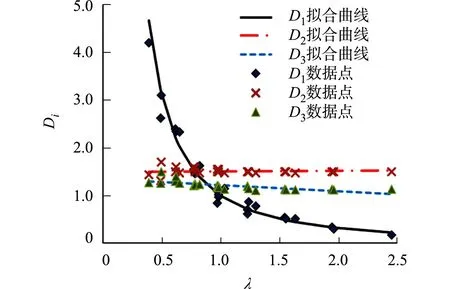
图6 网格密度与拟合系数曲线Fig.6 Curves of mesh density and fitting coefficient
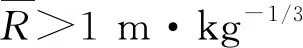
(8)
式(8)中:D1=2.34;D2=1.475;D3=1.265.
提取不同网格密度下的D1,D2和D3,得到网格密度与拟合系数曲线,如图6所示.根据各数据点的分布规律,将D1,D2和D3拟合为与网格密度λ相关的函数,即
(9)
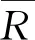
(10)
(11)
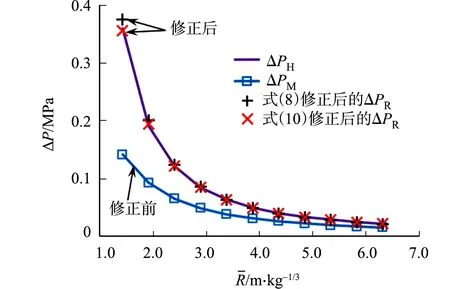
图7 修正前、后超压的对比Fig.7 Comparison of overpressure before and after correction
利用式(10),(11)或式(8)的修正系数,可以快速修正数值模拟的ΔPM,修正后的冲击波超压ΔPR表达式为
ΔPR=η×ΔPM.
(12)
以λ=0.65的算例为例,提取11个测点,将修正后的ΔPR与ΔPH进行对比.修正前、后超压的对比,如图7所示.由图7可知:修正后的超压值与经验公式计算值ΔPH吻合良好;分析11个测点的数据,按式(8)或式(10)修正后,ΔPR相对于ΔPH的最大误差分别为4.2%和1.8%,误差较小.
3.2 修正系数式2
由节2.1的分析可知,根据Henrych的经验公式(式(4))计算出的超压峰值偏小,存在低估爆炸冲击波荷载的风险;而吴彦捷等[9]综合21组经验公式的超压平均值,拟合获得的超压计算公式(式(5))更具有参考意义,计算出的超压ΔPW也更为安全.因此,以ΔPW作为修正目标,再次进行模拟超压ΔPM的修正拟合.与式(10),(11)的拟合方法相同,先计算并拟合出不同网格密度λ下的D1,D2和D3,再将D1,D2和D3拟合为与λ相关的函数,最终获得修正系数式为
(13)
(14)
3.3 理想刚性墙面反射超压的估算与验证
在获得修正系数η之后,即可按照式(12)修正低成本粗网格模型的模拟超压,获得较为精确的估算超压值.为了检验估算超压的准确性,模拟计算刚性墙面的反射超压,并与理论值进行对比.对于无限大的理想刚性墙面,李翼祺等[19]给出了正反射超压ΔP2与入射超压ΔP1之间的关系式,即
(15)
式(15)中:P0为标准大气压,取0.1 MPa.以W=100 kg为例,根据式(4)计算得到入射超压ΔP1=0.078 4 MPa,代入式(15),即可算得的理论上的ΔP2=0.204 MPa.
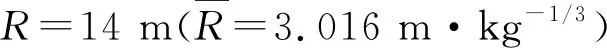

表3 理想刚性墙面反射超压估算Tab.3 Estimation of reflection overpressure on ideal rigid wall
由表3可知:经过超压修正后,超压误差δ明显减小,修正效果良好.利用粗网格(λ为0.49,1.23)模拟并修正后的ΔPR-H,可以获得与细网格(λ为2.50,4.90)的ΔPM相当的模拟精度,且只需要细网格模型的1/125,甚至更少的单元数量,极大地降低了计算成本.
3.4 封闭空间内爆炸的超压估算与验证
为进一步验证文中估算方法的有效性和准确性,对试验模型进行超压估算.文献[20]中进行的封闭空间内爆炸试验示意图,如图8所示.试验模型采用150 mm厚的钢筋混凝土制成,内壁布置了5个超压测点(1#~5#).试验分别进行多个炸药量(W分别为75,150,200,300,500 g)的内爆炸,起爆点均设在模型的几何中心处.根据对称性,建立1/8模型,空气域尺寸(长×宽×高)为0.8 m×0.8 m×1.6 m,以b=0.025 m进行网格划分,同时,按照图8布置刚性墙面,建模方式同节3.3.封闭空间内爆炸数值模型示意图,如图9所示.
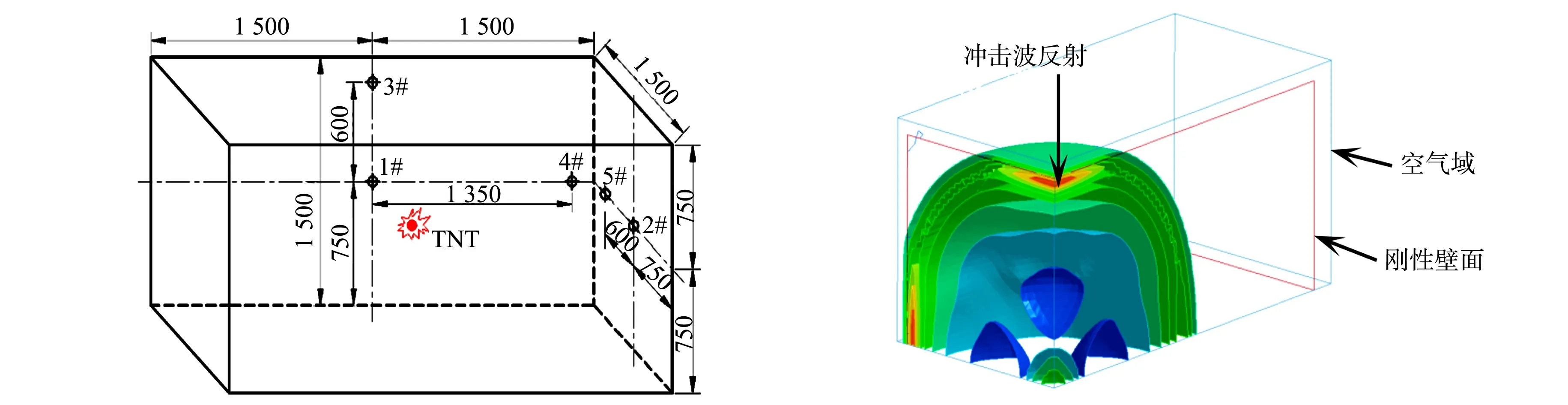
图8 封闭空间内爆炸试验示意图(单位:mm) 图9 封闭空间内爆炸数值模型示意图 Fig.8 Schematic of explosion test Fig.9 Schematic of explosion numerical in closed space (unit: mm) model in closed space
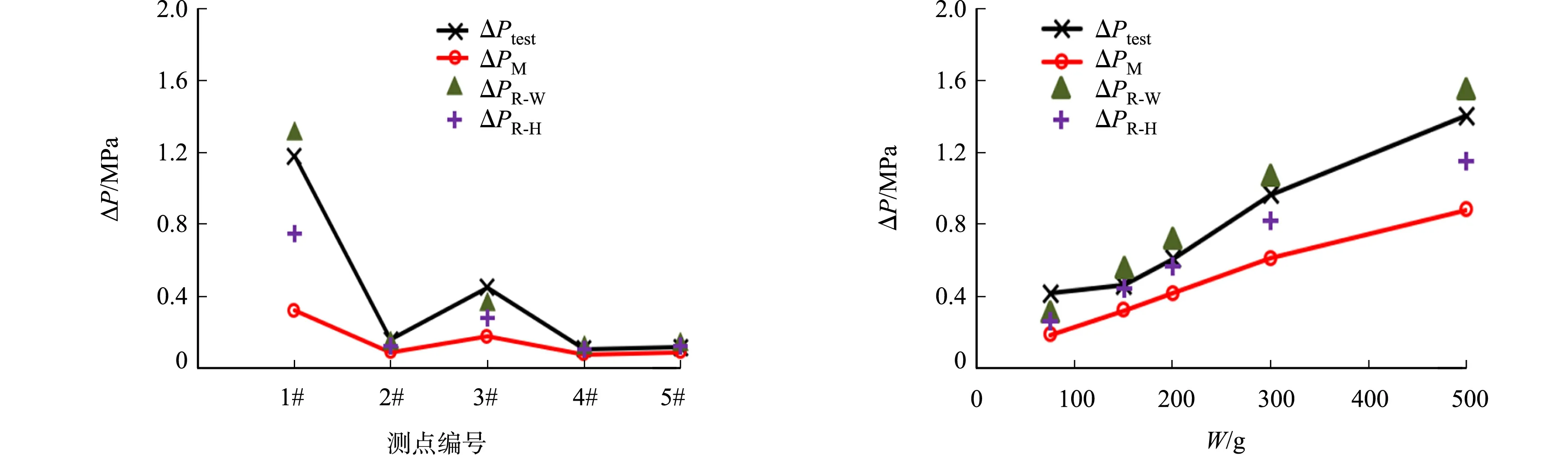
(a) 第一峰值(W=75 g) (b) 最大峰值(2#测点)图10 超压实测值与估算值的对比Fig.10 Comparison of overpressure test values and estimated values
取W=75 g(λ=0.89)进行模拟,并提取各测点超压时程曲线的第一次峰值(ΔPM),再分别利用式(10),(11)和式(13),(14),计算修正后的超压ΔPR-H和ΔPR-W,结果如图10(a)所示.图10(a)中:ΔPtest为实测超压.由图10(a)可知:修正结果明显降低了超压误差,各测点的修正超压与实测超压吻合较好;仅1#测点和3#测点的ΔPR-H偏小,正如节3.2所述,ΔPR-H存在低估超压的风险.将1#,3#测点的ΔPM按照式(13),(14)进行修正后,两个测点的ΔPR-W与ΔPtest的误差仅为11.6%和17.2%,与细网格的模拟精度相当,说明通过两组修正公式的互补可以较好地控制误差.
封闭空间内爆炸的超压曲线具有多峰值的特点,2#测点实测超压时程曲线的最大峰值均大于第一次峰值.因此,进一步模拟并提取不同W下,2#测点的超压最大峰值,将修正超压与实测超压进行对比,如图10(b)所示.由图10(b)可知:除W=75 g的工况外,其他弹药量下的ΔPtest均介于ΔPR-H和ΔPR-W之间,且误差基本控制在20%以下,达到细网格的模拟精度要求.
综上所述,利用文中估算方法获得的修正超压与理论值和试验实测值吻合良好.限于篇幅,文中仅验证了刚性壁面环境下的模拟超压值.对于考虑壁面刚度和壁面破坏等更为复杂情况下的超压场,修正公式的准确性还有待进一步验证.将实际壁面假设为刚性壁面进行模拟,由于未考虑壁面的耦合吸能,会使反射超压偏大,计算获得的超压场偏保守,因此,可以将其作为实际壁面环境下超压场的上限值.
4 结论
为了确定复杂环境下的爆炸超压场,提出利用粗网格建立低成本模型,再对模拟超压进行修正,以获得高精度超压的快速估算方法,得到以下3点结论.
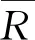
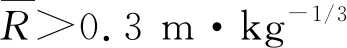
3) 利用拟合的冲击波超压修正系数公式,能够有效地对网格密度小于λlim的粗网格模型进行超压修正,获得较为精确的估算超压.通过估算超压与理论值、试验实测值的对比,验证提出的超压估算方法是可行的,且可以大幅度降低计算成本,为复杂环境下的超压荷载计算提供参考.
