连续微线段柔性加减速自适应前瞻规划算法
2021-02-01叶衡谢明红
叶衡, 谢明红
(华侨大学 机电及自动化学院, 福建 厦门361021)
大多数数控机床只具有直线和圆弧插补功能,随着加工零件曲面曲线的日益复杂,直接描述零件轮廓已不太可能.目前,数控机床在加工零件时,先由计算机辅助制造(CAM)软件将工件的复杂轮廓曲线逼近成大量连续且短小的微线段,这些线段的长度通常为0.1~1.0 mm.采用传统的加减速与插补算法时,数控机床将每段微线段内独立加减速,起始点速度设置为零,机床在每段加工轨迹内频繁启停,极大限制了机床能达到的进给速度,使机床各轴的加减速能力无法得到充分利用,同时,机床的频繁启停会造成震动与冲击,降低工件的加工质量.为了解决这些问题,国内外学者进行了大量的研究[1-3].较为常用的前瞻算法的核心是加减速算法和拐点处的速度约束.王耀庭等[4]提出一种基于直线加减速方式的高速嵌入式数控系统速度前瞻算法,但直线加减速方式柔性差,对机床仍有冲击.钟前进等[5]研究S曲线加减速,并将其用于数控系统,提高了数控加工的速度和柔性,但该方法计算复杂,不利于实时处理.司慧晓等[6]将完整的S曲线加减速进行简化.
目前,具有前瞻功能的数控机床大多采用固定段数的前瞻方式,前瞻段数达数千甚至上万,极大地占用数控系统的内存资源,降低处理效率.因此,王海涛[7]根据加工轨迹拐角的大小区分前瞻区间,自适应地调整前瞻段数[7],但其速度敏感点的识别方式仍可能使前瞻段数过多.许东伟[8]提出一种以最大速度减速至零走过的段数区分前瞻区间的方法,可缩短前瞻区间,但在敏感点为零时,该方法的速度规划无法达到最优.基于此,本文提出一种连续微线段柔性加减速自适应前瞻规划算法.
1 S曲线加减速
1.1 加减速原理
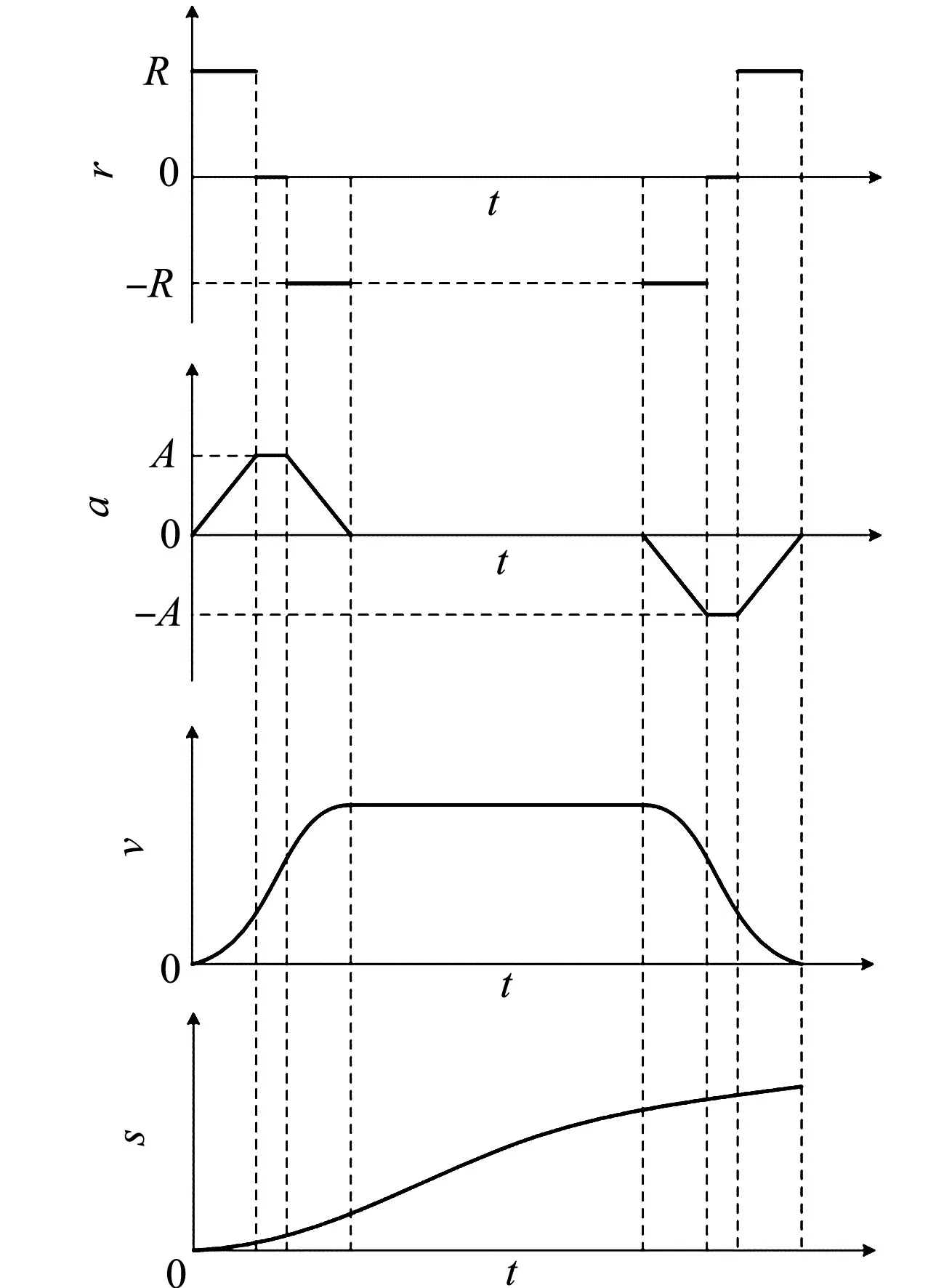
图1 简化的S曲线加减速Fig.1 Simplified S-curve acceleration and deceleration
直线加减速[9]柔性较差,而完整的S曲线加减速则计算复杂[10].简化的S曲线加减速,如图1所示.图1中:s为位移;v为进给速度;a为加速度;r为加加速度;R为加加速度最大值;-A为系统允许反向进给加速度的最大值;A为系统允许进给加速度的最大值.简化的S曲线加减速分为加加速段T1、减加速段T2、匀速段T3、加减速段T4、减减速段T5等5个时间段[11].
由于电机在加加速段与减加速段的加加速度绝对值相等,故有
T1=T2=R/A.
(1)
同理,有
T4=T5=R/A.
(2)
故有
T1=T2=T4=T5.
(3)
数控系统允许进给速度最大值vmax及R,A是确定的,故S曲线加减速过程可确定.在完整的S曲线加减速中,加加速度r为
(4)
式(4)中:t1~t5为各阶段的时间节点.
加速度函数a(t)、进给速度函数v(t)和位移函数s(t)可通过积分得到,即

(5)

(6)

(7)
式(5)~(7)中:ti为时间节点;τi表示以ti-1为起点的时间.
刀具起始点速度均为0(图1),可以达到系统允许的加速度和速度,其加加速度r越大,达到系统允许最大加速度的时间T1越小,柔性越差;反之,柔性越好.
1.2 段内加减速等效模型
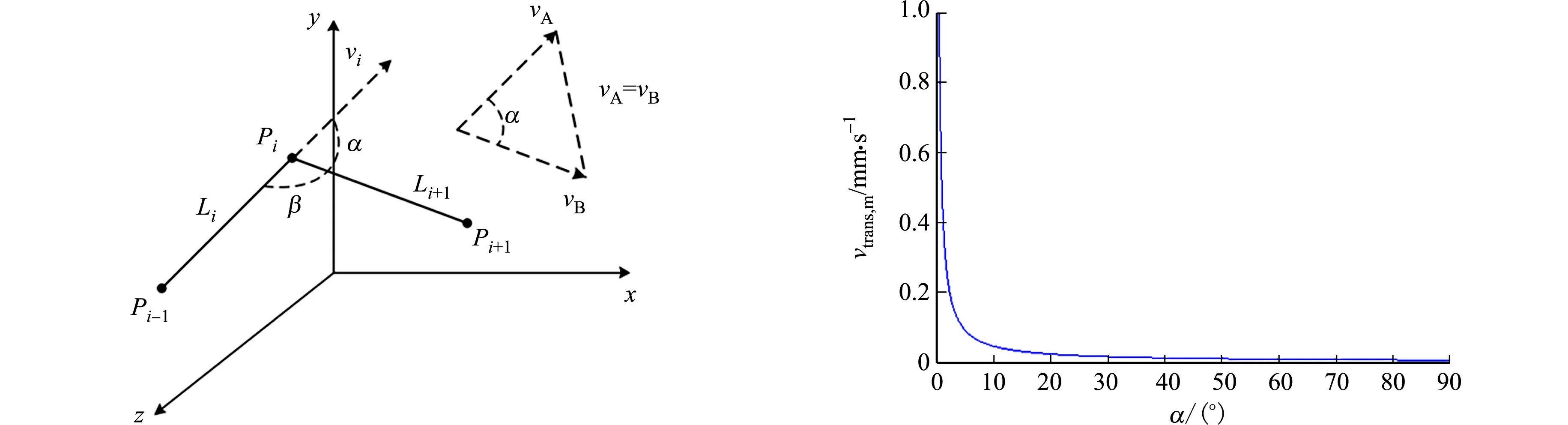
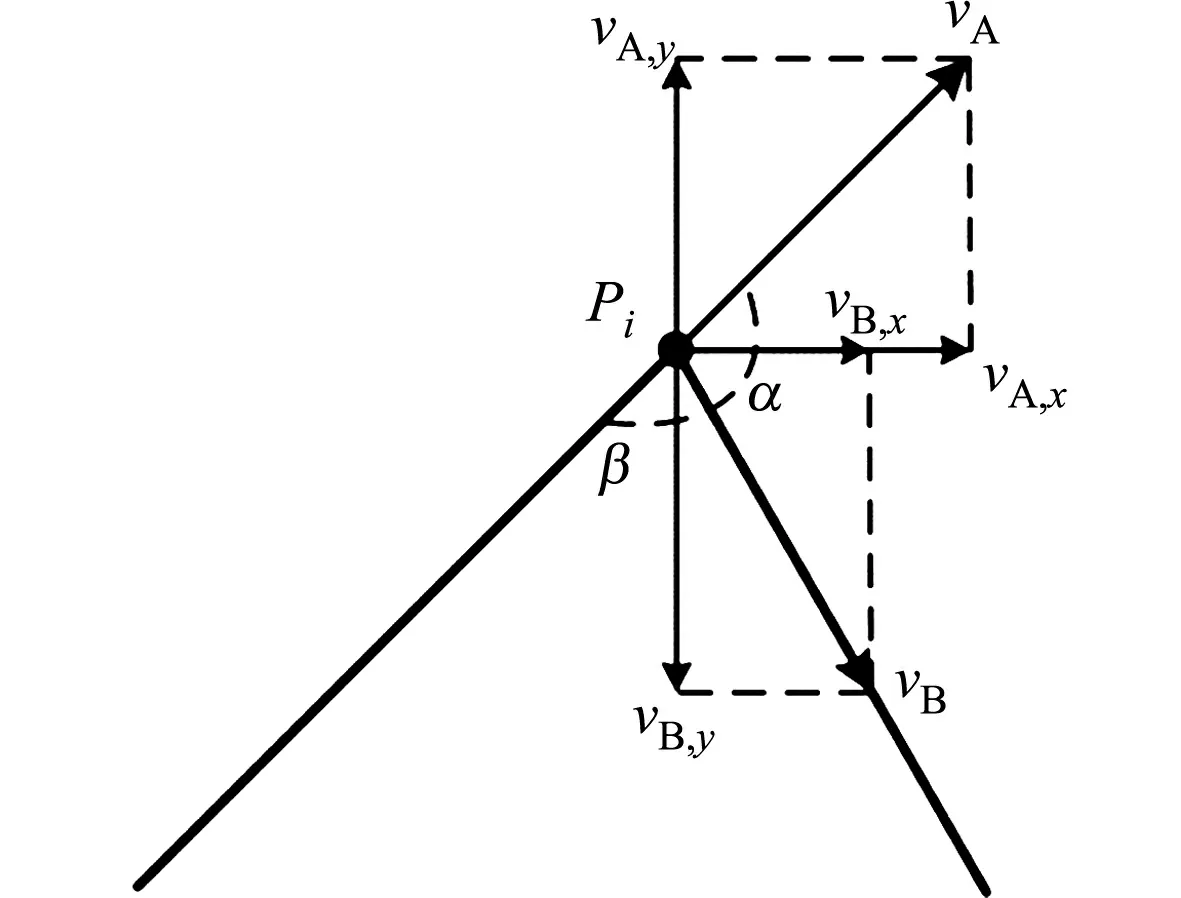
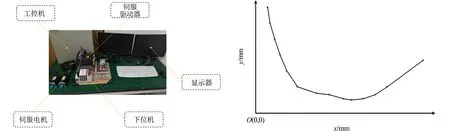
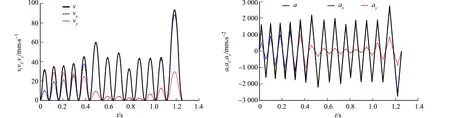
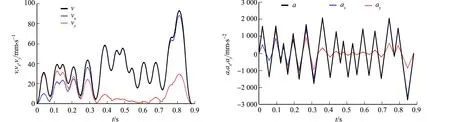
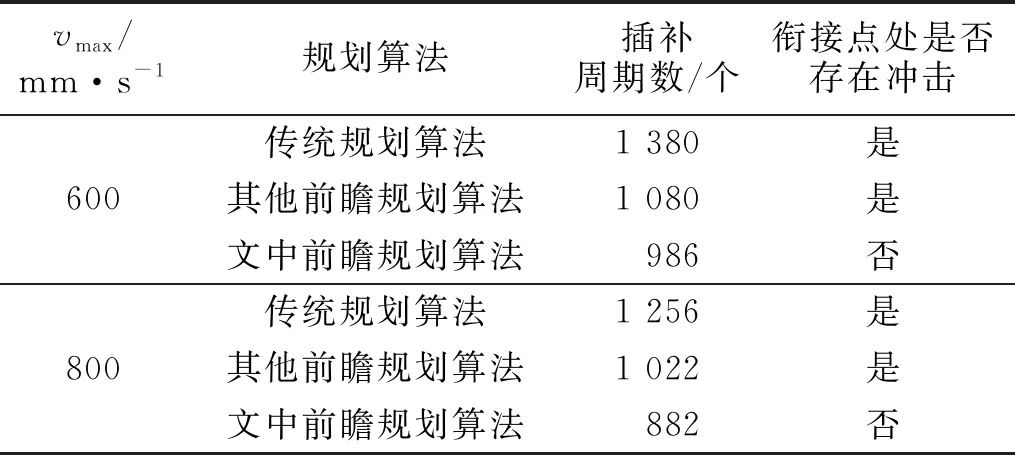
在实际加工中,因各段轨迹长度限制,进给速度不一定可以达到vmax,且电机在加工轨迹的起始点速度不一定为0.设起始速度为vs,终点速度为ve,可达到的最大速度为vm.当vs 1) 2段加减速(图2(a)).只有T1,T2或T4,T5段;vs>ve同理. 2) 完整加减速(图2(b)).当vm=vmax时,具有完整的加减速过程,T1=T2,T4=T5;vs>ve同理. 3) 4段加减速(图2(c)).当vm (a) 2段加减速 (b) 完整加减速 (c) 4段加减速图2 段内实际加减速情况Fig.2 Actual acceleration and deceleration within segment 设轨迹长度为L;电机从vs加速到vmax,刀具所走过的位移为Lac;电机从vmax减速到ve,刀具所走过的位移为Lde;电机从vs加速或减速到ve,刀具所走过的位移为l.由式(4)~(7)可得 (8) (9) 假设vs>ve(vs (10) 当L>Lac+Lde时,加工轨迹长度足够电机加速到vmax;当l (11) 传统方法无法精确求解vm,有的文献采用牛顿迭代法,但该法迭代次数过多,计算过程相对耗时.因此,采用二分法求解,设定误差范围为0.1,则有 (12) Li段与Li+1段的交点为Pi,刀具的运动方向为Pi-1→Pi→Pi+1.刀具在Pi-1的速度为vi-1,在Pi的速度为vi,在Pi+1的速度为vi+1.在Li段,刀具在点Pi的进给速度为vA,方向由Pi-1指向Pi;在Li+1段,刀具在点Pi的进给速度为vB,方向由Pi指向Pi+1.在机床加工中,设定刀具在Pi处的速度大小相等,方向发生了改变,|vA|=|vB|;vA与vB的夹角为α,线段Li与Li+1的夹角为β.拐点示意图,如图3所示. 1) 拐角角度对速度的约束.因为刀具在点Pi的速度发生变化,且速度改变发生在1个插补周期内,所以刀具在拐点Pi处产生加速度atrans.为避免对机床产生冲击,应使atrans不超过机床允许的最大加速度amax. 设插补周期为Ts,则atrans满足 (13) 由此可得 (14) 式(13),(14)中:Δv为速度变化量;vtrans为拐角角度的约束速度. 拐角角度的速度约束,如图4所示.图4中:vtrans,m拐角角度的最大约束速度. 图3 拐点示意图 图4 拐角角度的速度约束Fig.3 Diagram of corner point Fig.4 Speed constraint of corner angle 2) 微线段长度对速度的约束.刀具运动的方向为Pi-1→Pi→Pi+1,vi-1 Ⅰ)vi受Li长度的影响.若Li>Lac,则刀具有足够的加工长度,刀具在点Pi的速度不受Li长度的限制,即 vi=vmax. (15) 若Li (16) 刀具由vi-1加速到vi的过程由T1,T2组成,令T1=T2=tm.由式(4)~(7)可得 (17) 通过卡丹公式求解一元三次方程,可得 (18) 式(18)中:p=2vi-1/R;q=-Li-1/R. 由式(4)~(7)可得 (19) 由此可得 (20) Ⅱ)vi受Li+1长度的影响.同理可得 (21) 式(21)中:p=2vi+1/R;q=-Li+1/R. 图5 拐角速度突变示意图Fig.5 Diagram of abrupt change of corner speed 前瞻的主要任务是预先获取一定数量的加工轨迹信息,并对其进行速度规划.当其他条件不变时,前瞻段数越多,则速度规划效果越优.目前,具有前瞻功能的机床常用的方式是每次前瞻一定数量的轨迹段或规划所有的轨迹段,但这种做法缓冲区占用的内存较大,且固定段数的前瞻不适应加工轨迹间速度变化的要求.此外,因为拐角角度的限制,有些拐角处的速度极低,甚至减速为0,这些拐角两端加工轨迹处的速度不会相互影响,所以将两端处轨迹结合前瞻没有意义.为解决这些问题,采用识别速度敏感点的方法分割前瞻区间,实现自适应动态前瞻. 拐角速度突变示意图,如图5所示.图5中:vA,x,vB,x分别为vA,vB在x轴上的分量;vA,y,vB,y分别为vA,vB在y轴上的分量.当拐角β<90°时,刀具在拐点Pi的速度在y轴的分量方向在一个周期内发生逆向突变,此时,y轴电机需要在非0速度下进行反转,对电机冲击较大,故此点速度极低.将此点设为速度敏感点,相邻敏感点之间的加工轨迹为一个独立前瞻区间. 传统的前瞻算法将敏感点的速度设置为0,这种做法虽然可避免电机在非0速度下进行反转,但会降低加工效率,且造成机床频繁启停,从而引入其他加工误差.因此,假定刀具从敏感点运动到下一点时,其速度可以减小为0,根据拐角角度和敏感点后一段加工轨迹长度的限制,计算敏感点安全加工速度,可得 (22) 式(22)中:vlim为敏感点的安全过渡速度;Lnext为敏感点后一段加工轨迹长度. 完成对加工轨迹的独立前瞻区间分段后,需要对区间内的轨迹段进行速度规划,结合前推法和回溯法[12-18]提出前瞻规划策略.设现有一个独立前瞻区间,拐点分别为Pi-1~Pi+5;轨迹段分别为Li~Li+5;设αn为点Pn处拐角,n=i-1,i,…,i+5;由Sif判断点Pn是否敏感点,若为Y,表示是敏感点,若为N,表示非敏感点;vtrans_n为点Pn处拐角限制的最大速度(式(14));vpre_n为点Pn前一段加工轨迹长度限制的最大速度(式(20));vnext_n为点Pn后一段加工轨迹长度限制的最大速度(式(21));vn为点Pn的最优最大速度.前瞻前将每点的速度初始化,即vn=0,Sif为N.前瞻规划策略有以下6个步骤. 步骤1从插补轨迹第1段开始,依次计算每个拐角αn.当αn<90°时,将Sif设置为Y;否则,设置为N.将2个相邻Sif标志为Y的点之间的轨迹段设置为1个独立区间.从第1个独立前瞻区间开始前瞻. 步骤2根据式(22)计算终点Pn处的最优最大速度vn=vlim,n=i+5. 步骤3令n=n-1,若n=i-1,开始步骤5;否则,向前读取下一点Pn,分别计算vtrans_n,vnext_n.如果vtrans_n>vnext_n,则vn=vnext_n,重复该步骤;如果vtrans_n 步骤4若vi>vi+1,结束该步骤;否则,计算vpre_i+1.判断是否vpre_i+1>vi+1,若是,则结束该步骤;否则,vi+1=vpre_i+1且i=i+1,重复该步骤,直至vpre_i+1>vi+1,开始步骤3. 步骤5令n=n+1,若n=i+5,结束该步骤;否则,向后读取下一点Pn,计算vpre_n.若vpre_n>vnext_n,结束该步骤;若vpre_n 步骤6该前瞻区间结束,判断是否前瞻完成,若完成,则结束前瞻;否则,读取下一前瞻区间,转入步骤2. 适用于连续微线段加工的新型前瞻规划算法(文中前瞻规划算法)采用先回溯再前推的方法,避免前瞻缓冲区过大的问题,且进一步优化敏感点的速度,使其不为0,可提高加工效率. 实验平台包括硬件平台和软件平台.硬件平台由空气开关、电源、工控机(上位机)、CX5020型下位机(德国倍福自动化有限公司)、伺服电机、伺服驱动器等通过导线和通信线(双绞线)进行连接.实验硬件平台,如图6所示.软件平台的开发环境采用基于Windows系统的Visual Studio,编程语言采用面向Windows的Visial C++.采用EtherCAT总线技术实现与伺服驱动器的实时通信,由数控系统计算插补点,发送插补周期给伺服驱动器,进而驱动电机,通过编码器采集速度. 微线段的加工轨迹,如图7所示.设机床最大允许加速度为8 000 mm·s-2,最大允许加加速度为80 000 mm·s-3,插补周期Ts=1 ms.在不同机床允许的最大速度(vmax分别为600,800 mm·s-1)下,分别采用传统规划算法、其他前瞻规划算法和文中前瞻规划算法进行对比实验.其他前瞻规划算法与文中前瞻规划算法衔接点(拐角点)的速度,如表1所示. 图6 实验硬件平台 图7 微线段的加工轨迹Fig.6 Experimental hardware platform Fig.7 Machining trace of micro line 表1 前瞻规划算法衔接点的速度Tab.1 Junction points speed of look-ahead planning algorithm 当vmax=800 mm·s-1时,传统规划算法的插补输出情况,如图8所示.图8中:v,vx,vy分别为传统规划算法的插补输出速度(进给速度)及其在x,y轴上的分量;a,ax,ay分别为插补输出加速度(进给加速度)及其在x,y轴上的分量. (a) 插补输出速度及其分量 (b) 插补输出加速度及其分量图8 传统规划算法的插补输出情况Fig.8 Interpolation output situation of traditional planning algorithm 由图8可知:采用传统规划算法进行加减速插补时,刀具在各衔接点的速度降为0,各微线段内独立加减速.因为微线段长度限制,刀具在各段内可达到的最大进给速度很小,加速度波动较大,机床加工效率低下,电机在拐角处频繁启停造成机床震动,影响工件加工质量. 当vmax=800 mm·s-1时,其他前瞻规划算法的插补输出情况,如图9所示.由图9可知:其他前瞻规划算法通过设置拐点,将加工轨迹分为独立区间,并在独立区间内独立加减速,相较于传统规划算法,可实现独立区间内的连续速度规划,提高加工效率,减少电机启停的次数,提高机床的加工精度,但仍不能保证在衔接点处的速度均大于0.电机对机床仍有冲击,不利于机床进一步提高速度和精度. (a) 插补输出速度及其分量 (b) 插补输出加速度及其分量图9 其他前瞻规划算法的插补输出情况Fig.9 Interpolation output situation of other look-ahead planning algorithm 当vmax=800 mm·s-1时,文中前瞻规划算法的插补输出情况,如图10所示.由图10可知:采用文中前瞻规划算法对加工轨迹进行规划时,除起点和终点外,衔接点速度均大于0,且段内可达到的进给速度明显增大,加工效率较高,加速度波动小,机床不容易产生冲击. (a) 插补输出速度及其分量 (b) 插补输出加速度及其分量图10 文中前瞻规划算法的插补输出情况Fig.10 Interpolation output situation of proposed look-ahead planning algorithm 表2 3种规划算法的输出结果Tab.2 Output results of three algorithms 3种规划算法的输出结果,如表2所示.由表2可知:相较于传统规划算法和其他前瞻规划算法,文中前瞻规划算法可以缩短加工时间.当vmax=600 mm·s-1时,文中前瞻规划算法的加工效率比传统规划算法提高了28.6%,比其他前瞻规划算法提高了8.7%;当vmax=800 mm·s-1时,文中前瞻规划算法的加工效率比传统规划算法提高了29.8%,比其他前瞻规划算法提高了13.7%. 提出一种适用于连续微线段加工的新型前瞻规划算法,采用简化的S曲线加减速,减少计算时间,通过识别速度敏感点自适应调整前瞻区间,解决了传统前瞻算法前瞻段数过多的问题;进一步优化前瞻区间的终点速度,使其大于0.相较于其他算法,文中前瞻规划算法可进一步提高衔接点速度、加工平稳性及加工效率.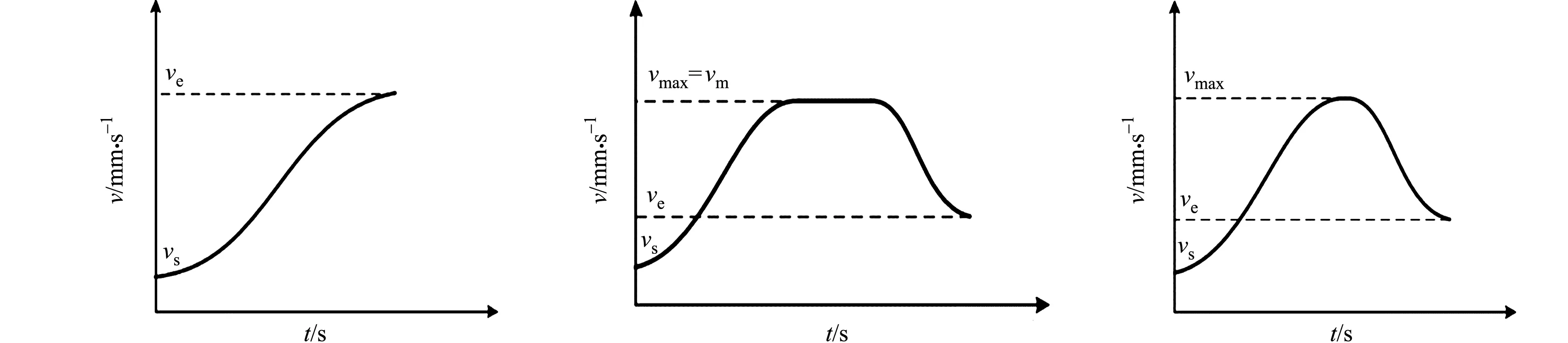
2 自适应前瞻速度规划
2.1 拐点处速度约束
2.2 自适应前瞻分段规划
2.3 前瞻速度规划
3 实验验证
3.1 实验平台的搭建
3.2 连续微线段的取样验证


4 结束语
