复杂环境下移动机器人路径规划算法

贾丙佳， 李平

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

随着科学技术的发展和生活水平的提高，智能移动对象(移动机器人)逐渐融入人们的日常生活中，如家庭扫地机器人[1]、商场导购机器人[2]等.智能移动对象能在工作空间中按照一定的性能指标，如花费的时间最少、所走的路径最短等，从起始点到目标点搜索一条最优或次优的无碰路径[3-4].路径规划是研究这类机器人的核心，众多研究者对移动机器人路径规划展开大量的研究.根据移动对象对环境的掌握程度，移动机器人路径规划问题可分为两个分支：1) 静态全局路径规划， 在环境信息已知的情况下，根据给定的起始点和目标点，机器人能够搜索出一条最优路径，这要求当前环境必须和机器人所掌握的环境一致，且没有移动障碍物；2) 动态局部路径规划，对于部分环境信息无法获取或环境中出现移动物体的情况，机器人需要自行探测环境信息，对将要行走的路径实时做出调整，以确保机器人和其他移动物体的安全[5-6].

目前，解决静态全局路径规划的算法有栅格法[7]、可视图法[8]、自由空间法[9]和A star(A*)搜索算法[10]等.栅格法将地图划分成一个个单元格，根据单元格的信息对环境进行感知，单元格的大小会影响路径规划的精度与效率；可视图法和自由空间法的共同缺点是对环境中的所有障碍物均做连线处理，对机器人行走不到的无效区域的处理暴露了算法的冗余性；A*搜索算法根据节点代价值的高低进行扩展，具有较好的实时性，但不能保证搜索的路径全局最优.然而，智能移动对象所处的环境不能满足静态的需求，而且随着移动机器人技术的发展和应用领域的扩大，迫切要求机器人能够适应动态、复杂多变的环境[11-12].因此，在局部动态环境下，要求机器人能够利用自身携带的测量装置，实时探测周围变化的环境信息.动态局部路径规划算法有人工势场法[13-14]、遗传算法[15]、神经网络法[16]和模糊逻辑法[17]等.人工势场法存在局部极小值和目标不可达的问题.郜辉等[18]、韩知玖等[19]和徐飞[20]通过增加中间子目标的方法解决局部极小值问题；Lee等[21]改进选择算子解决遗传算法收敛速度慢的问题，并提出快速遗传算法.神经网络法通过对环境地图的学习，能够实现对机器人的自主导航，但对动态变化的现实环境，需要重新学习.模糊逻辑法并不需要对环境中的障碍物信息进行精确计算，但当环境中的障碍物数量过多，建立模糊规则时的复杂度将显著增加，降低了动态路径规划的效率.这些方法对解决路径规划问题起到一定的作用，但均存在不足之处.本文针对移动机器人所处的复杂环境，提出一种全局-局部混合模式的路径规划方法.

1 全局路径规划问题

图1 工作模式转换图Fig.1 Working mode conversion diagram

在全局环境下，自主移动机器人利用事先存储的全局静态环境信息，从指定的起始点到目标点规划出一条时间最短的无碰路径.此时，机器人工作在全局规划模式下，工作模式转换图，如图1所示.机器人工作在全局规划模式下，在安全区内探测到移动物体时，机器人进行一系列计算，判断是否应该转换工作模式；当机器人通过碰撞区，且安全区内没有其他移动物体时，则再次回到全局规划模式.

1.1 静态环境建模

根据事先存储的全局环境地图，机器人规划出一条从指定起始点到目标点的最优无碰路径.为简化分析，以质点表示障碍物的中心，以半径为ρobs的圆形表示障碍物的影响范围.

首先，读取环境地图，找出障碍物密集分布的区域，具体有以下3个步骤.

步骤1计算障碍物之间的距离.障碍物距离计算示意图，如图2所示.图2中：虚线圆表示障碍物的影响范围.距离d1，2的计算公式为

(1)

式(1)中：x1,x2为障碍物的横坐标；y1,y2为障碍物的纵坐标.

步骤2划分密集区域.运用阈值法对步骤1计算出的距离数据进行分类，找出邻近障碍物，划分出不同的密集邻近障碍物区域.密集障碍物区域划分结果，如图3所示.图3的阈值为2ρobs，如果距离数据小于等于2ρobs，则认为是相邻障碍物.

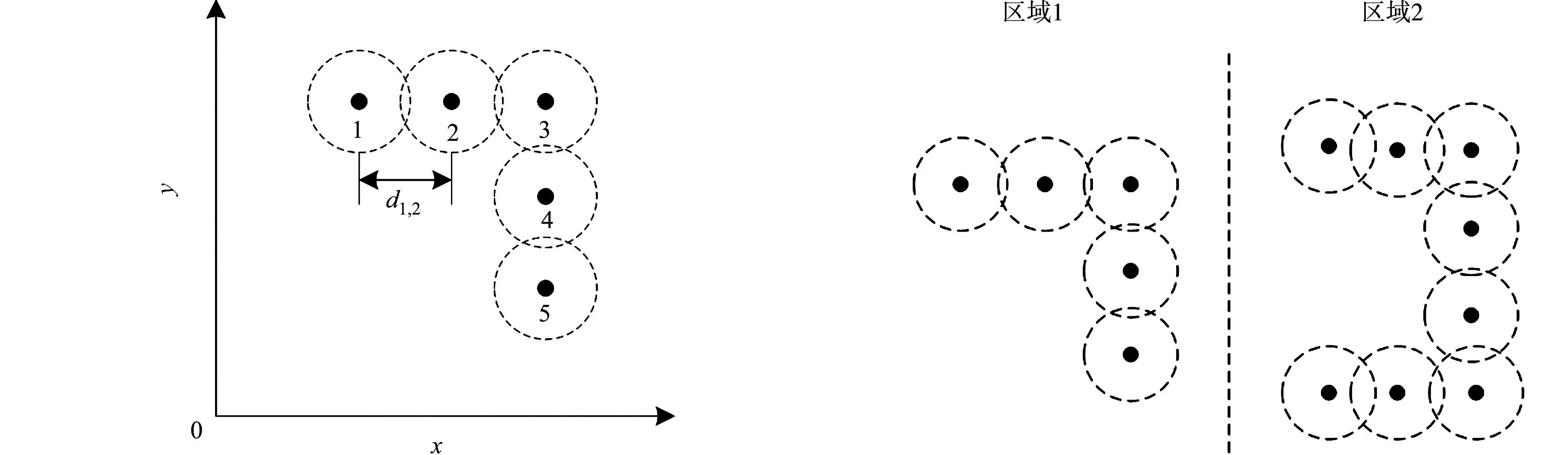
图2 障碍物距离计算示意图 图3 密集障碍物区域划分结果Fig.2 Schematic diagram of obstacle distance calculation Fig.3 Result of dense obstacle area division

步骤3整体化区域.首先，对每一个密集区域计算其最小包围矩形，矩形中心的计算公式为

(2)

式(2)中：x′，y′分别为矩形中心坐标；xmax，xmin分别为矩形横坐标的最大值和最小值；ymax，ymin分别为矩形纵坐标的最大值和最小值.

(3)

图4 障碍物整体化Fig.4 Integration of obstacles

1.2 全局路径规划

对建模环境进行处理，首先，画出起始点(xs,ys)到目标点(xg,yg)的连线，该连线为理想的最短路径.建立直线方程L1，有

(4)

然后，计算各个障碍物质心到直线L1的垂直距离d，密集区域的障碍物按照整体化后的中心进行计算，有

(5)

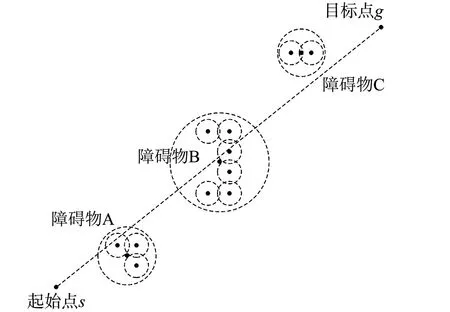
图5 路径简图Fig.5 Path sketch

式(5)中：A1，B1，C1均为直线方程L1的系数，A1=(yg-ys)/(xg-xs)，B1=-1，C1=(xgys-xsyg)/(xg-xs)；x0，y0为障碍物的横、纵坐标.

最后，进行垂直距离d和障碍物影响范围ρobs的比较.如果d≥ρobs，说明该障碍物附近的路径为有效路径；反之，则说明L1穿过障碍物区域，该区域内的路径为无效路径.

路径简图，如图5所示.图5中：障碍物C处为有效路径区域，障碍物A，B处为无效路径区域.无效路径的处理有以下3个步骤.

步骤1以起始点s为端点，计算出距离起始点最近的障碍物.在障碍物A处，以目标点为方向，画出与障碍物影响范围相切的两条射线，障碍物A处有两个交点(图6(a))，采用优先选择偏离目标方向较小角度的方法，确定角α，最终确定交点a.

步骤2以a为端点，画出其与目标点g的连接线，用步骤1的方法画出与障碍物B处相交的两条射线，获得点b(图6(b)).

步骤3以b为端点，画出其与目标点g的连接线，此时，障碍物C处变为无效路径区域，采用步骤1的方法，可获得点c.点c之后的路径全为有效路径，此时，直接连接目标点g(图6(c)).

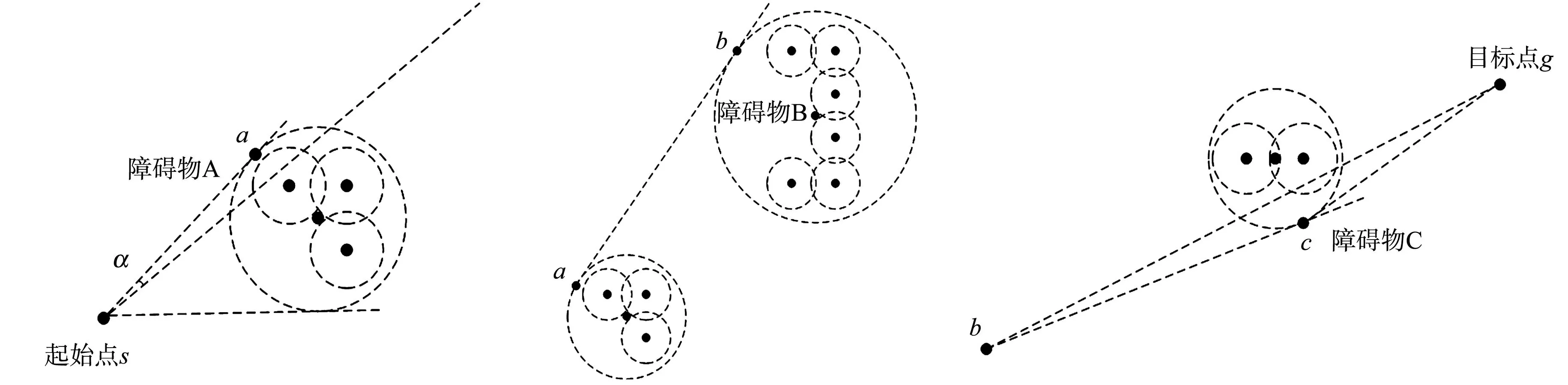
(a) 无效路径区域A (b) 无效路径区域B (c) 无效路径区域C 图6 子目标点分析Fig.6 Sub target point analysis

连接最初的点s，a，b，c,g，即可规划出一条全局路径.机器人从起始点s出发，依次沿直线通过子目标点a～c，最终到达目标点g.

图7 全局路径规划图Fig.7 Global path planning diagram

对静态环境进行处理时，将距离较近的多个障碍物视为一个整体，可减少密集障碍物区域路径规划的时间，也可减少极端情况下的迂回、循环路径.

最终的全局路径规划图，如图7所示.图7中：O1～O3为障碍物整体化之后的中心点；实线为规划出的全局路径；路径上的黑点为子目标点.在获得一系列子目标点及局部动态环境下的路径规划均采用人工势场法[11]驱动机器人向目标点移动.

2 局部路径规划问题

现实环境中有很多移动的物体，如环境中行走的人，且移动物体大都遵循恒定最大运行速度的直线运动，不会主动避开其他障碍物，当机器人探测到安全范围内有移动物体时，会对其运动路径进行预判，例如，对其速度、方向和未来移动路径进行计算，并根据计算结果选择合适的工作模式.

2.1 碰撞点检测

碰撞点检测，如图8所示.图8中:L1，L2分别表示机器人和物体的运动轨迹；v0为机器人运行的最大速度；v1为物体的运动速度；实线圆表示可能存在的碰撞点P; 实线箭头方向表示机器人和物体的移动方向;虚线表示机器人和物体的运动路径;小虚线圆表示移动物体的影响范围；大虚线圆表示机器人的安全范围；α′表示移动物体在机器人运动方向上的夹角.

(a) 无效碰撞点1 (b) 潜在碰撞点1 (c) 潜在碰撞点2 (d) 无效碰撞点2 (e) 无效碰撞点3 图8 碰撞点检测Fig.8 Collision point detection

机器人沿全局模式规划出的路径前进，在安全范围内探测到移动物体，假设移动物体朝着目标做匀速直线运动，正常情况下，机器人以最大速度v0恒速运行.机器人对移动物体进行计算，进而判断碰撞点是否有效(图8(a)～(c)).

通过检测装置测量出移动物体在相近时刻的两个位置点，便可获得移动物体速度的大小和方向，进而画出移动路径，计算该路径和机器人路径的交点，并判断交点处是否发生碰撞.由于障碍物正在进入或已经进入机器人探测范围(图8(d)，(e))，移动物体运动的路径和机器人的历史路径相交，交点不再对机器人产生影响.

2.2 碰撞点计算

移动物体的计算，如图9所示.图9中：D1，D2分别为ta到tb时间段内，机器人和物体的移动距离；D3，D4分别表示ta,tb时刻机器人距物体的距离；D5，D6分别表示在tb时刻，机器人和物体距离点P的距离；P为潜在碰撞点；P1，P3分别表示机器人和移动物体在ta时刻的位置；P2，P4分别表示机器人和移动物体在tb时刻的位置；αa，αb分别表示机器人在P1，P2位置时运动方向与物体的夹角.

图9 移动物体的计算Fig.9 Moving object calculation

机器人在地图中的运动位置已知，在没有探测到移动物体和进行移动物体分析时，机器人均保持最大速度v0匀速运行，即在D1段匀速运行.P3处的物体沿v1方向运动，P1处的机器人沿v0方向运动，在ta时刻测得物体到机器人的距离为D3，角度为αa，推算出P3的具体坐标为(x3,y3)；tb时刻物体运动到位置P4，机器人运动到位置P2，测得物体到机器人的距离为D4，角度为αb，推算出P4的具体坐标为(x4,y4).由式(1)可计算出D2，位置P1到P2的用时t1为

t1=ta-tb，

(6)

进而计算出物体的运动速度v1，即

(7)

机器人从位置P1运行到P2，路径线段L1已由全局路径规划给出，而物体运行到P3，P4可由机器人对应位置点推测得出，根据两点确定一条直线的原理(式(4))，确定物体的运行路径L2.然后，对L1，L2的交点P进行求解，求出点P的坐标为(xP,yP)；根据式(1)算出P到P4的距离D6，以及P到P2的距离D5.由此，可分别计算出点P2，P4到P的用时t2，t3，即

(8)

由D4～D6可计算出物体运动方向和机器人运动方向的夹角αP，即

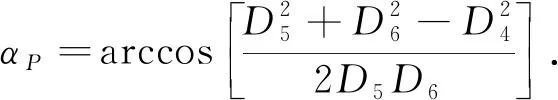
(9)

2.3 用时和速度分析

移动物体分析图，如图10所示.图10中：S1为临界位置；横向的3条虚线表示物体的移动区域，倾斜的3条虚线表示机器人前进路径的安全区域.当机器人以最大速度恒定运行时，t2为一确定值.移动物体存在以下3种情况.

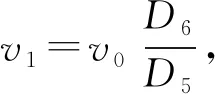
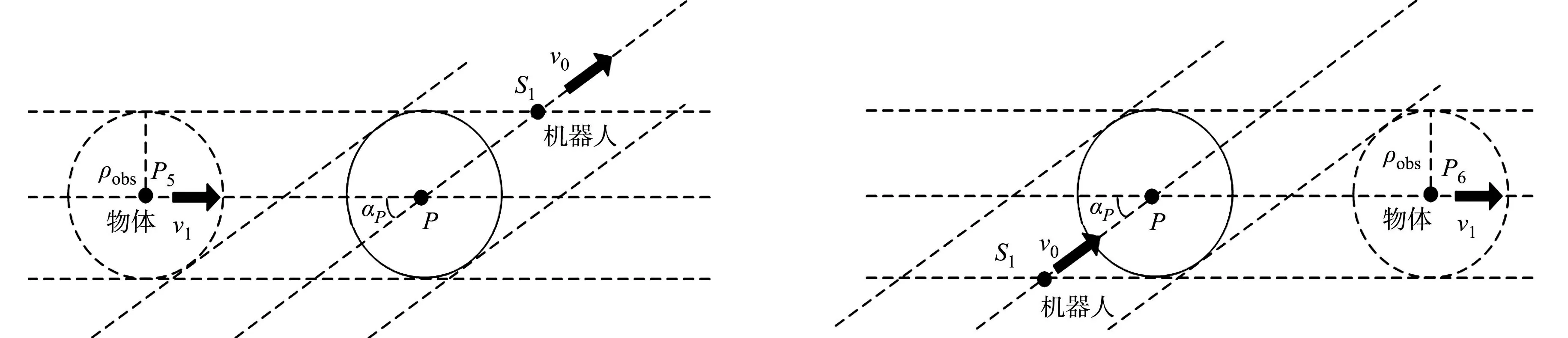
(a) 临界位置1 (b) 临界位置2 图10 移动物体分析Fig.10 Moving object analysis

情况1的机器人必须进行局部路径规划，而在情况2，3中，当机器人以v0运行到相应的位置S1，移动物体的速度没有超过上述的速度值时，均不会出现在碰撞区域内，则机器人可以按照全局规划的路径继续前行.

2.4 局部路径规划

情况2，3无需局部路径规划，情况1和除此以外的其他情况均需要进行局部路径规划.局部分析图，如图11所示.局部路径规划有以下3种方案.

(10)

由式(10)可得机器人减速为

(11)

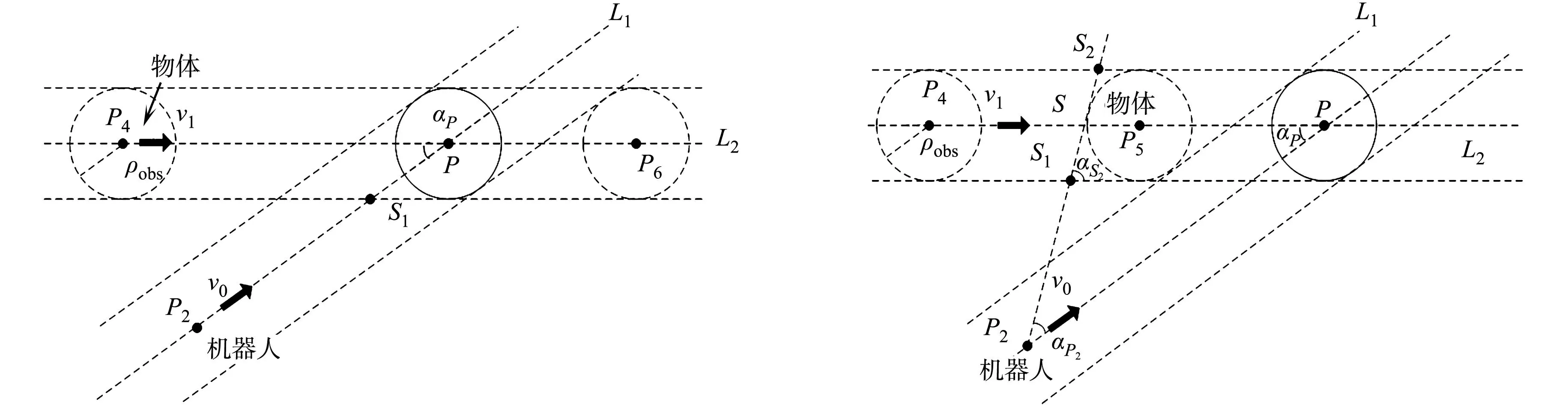
(a) 右范围处理 (b) 左范围处理图11 局部分析图Fig.11 Local analysis diagram

(12)

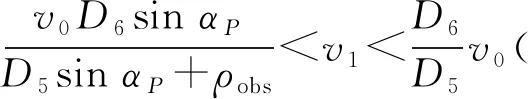
(13)

计算αP2，有

(14)

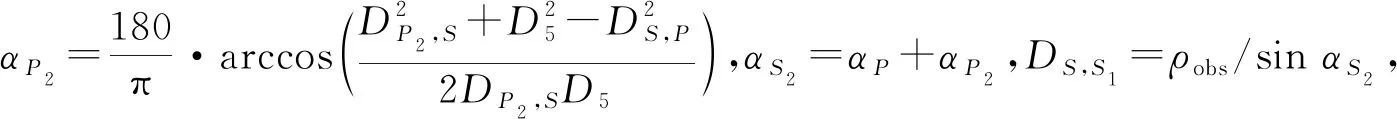
DP2，S1=DP2，S-DS，S1.

(15)

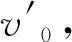
(16)

假设在该区间内物体以最慢速度移动到位置P5，为确保机器人不与物体发生碰撞，其减速且至多移动到位置S1，之后以同样的速度通过路径L2，到达位置S2时，若探测范围内没有其他移动物体，则以该点为新的起始点，重新规划一条到达目标点的路径，至此完成动态局部路径规划.

3 仿真与分析

为了验证所提方法的可行性和有效性，在MATLAB平台上进行仿真,将文中方法与经典人工势场法、改进人工势场法进行对比实验.设置移动机器人的工作空间为二维16 m×16 m的范围，空间中有11个静态障碍物和1个动态障碍物，设置障碍物的影响范围ρobs为0.5，整体化障碍物需按文中方法重新计算影响范围.以(0，0)为机器人起始点，(15，15)为目标点，机器人的最大速度v0=0.2 m·s-1，机器人有效探测范围为4 m.引用人工势场法作为机器人的引导和避障机制.

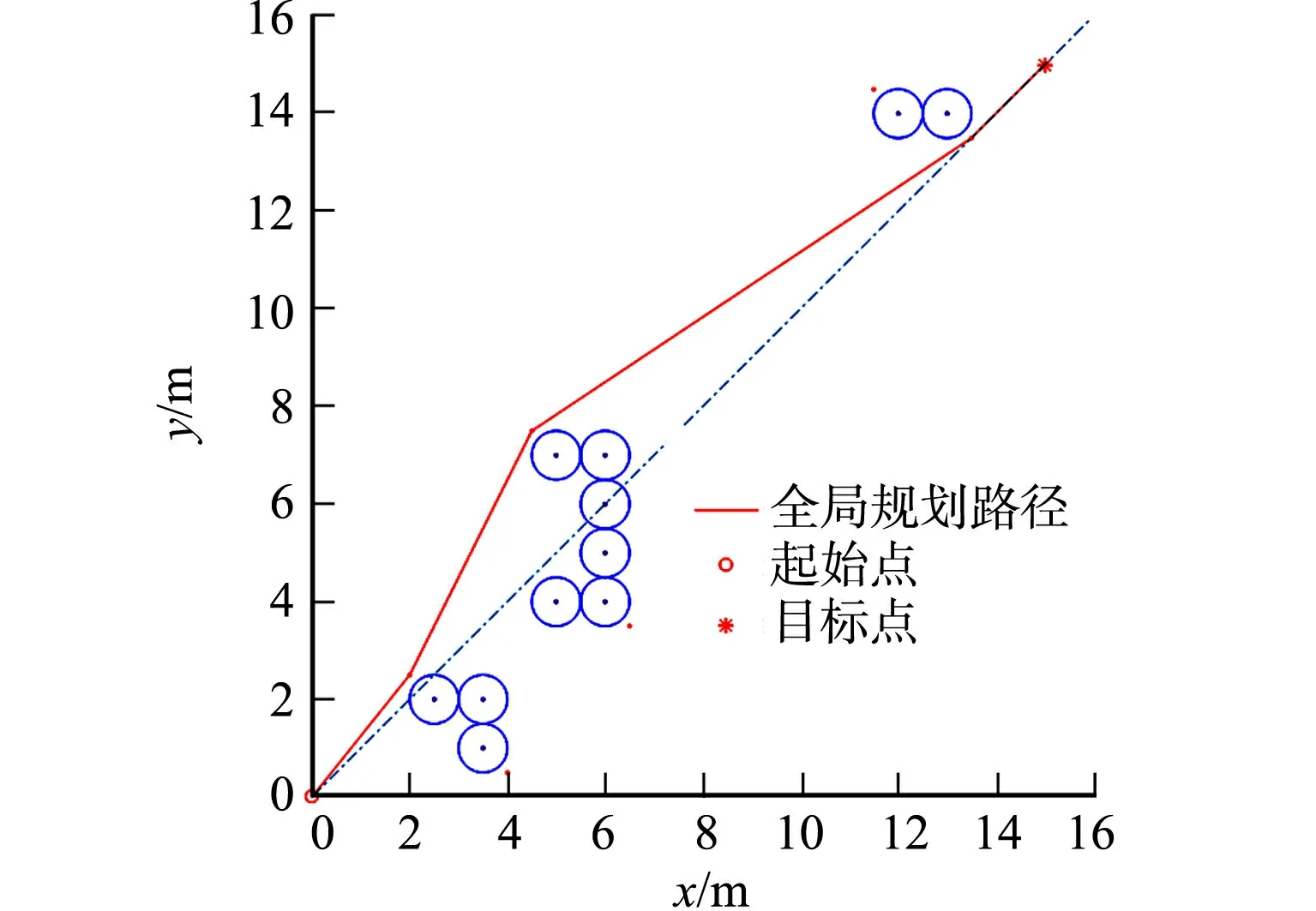
图12 全局路径规划示意图Fig.12 Schematic diagram of global path planning

3.1 全局路径规划仿真

全局路径规划示意图，如图12所示.图12中：全局路径规划没有移动的物体；虚线表示起始点到目标点的连线；全局规划路径上的点表示一系列子目标点；折线之外的点是依据节2.2原理被舍弃的点；圆圈中的圆点表示障碍物质心；圆圈表示障碍物影响范围.机器人以最大速度v0向一系列子目标移动，最终到达目标位置.

采用圆形区域对邻近密集分布的障碍物进行区域融合、替换，填补密集障碍物形成的凹陷区域，避免机器人陷入其中迂回、循环不前.同时，用圆形进行区域融合，具有后续计算便捷的优点.然而，圆形区域在一定情况下会损失部分可行路径，这是该方法的不足之处，将在今后的研究中解决.

3.2 局部路径规划仿真

机器人沿全局规划路径向前移动，假定开始移动时，在安全范围内没有移动物体.如果前进过程中，在安全范围内探测到移动物体，则根据计算结果决定是否进行局部路径规划，仿真结果如图13所示.图13中：动态障碍物由左向右移动，右上方倾斜和右下方倾斜的条形区域即为物体和机器人的移动区域，条形区域交叉形成的菱形区域表示移动物体和机器人的潜在碰撞区域.

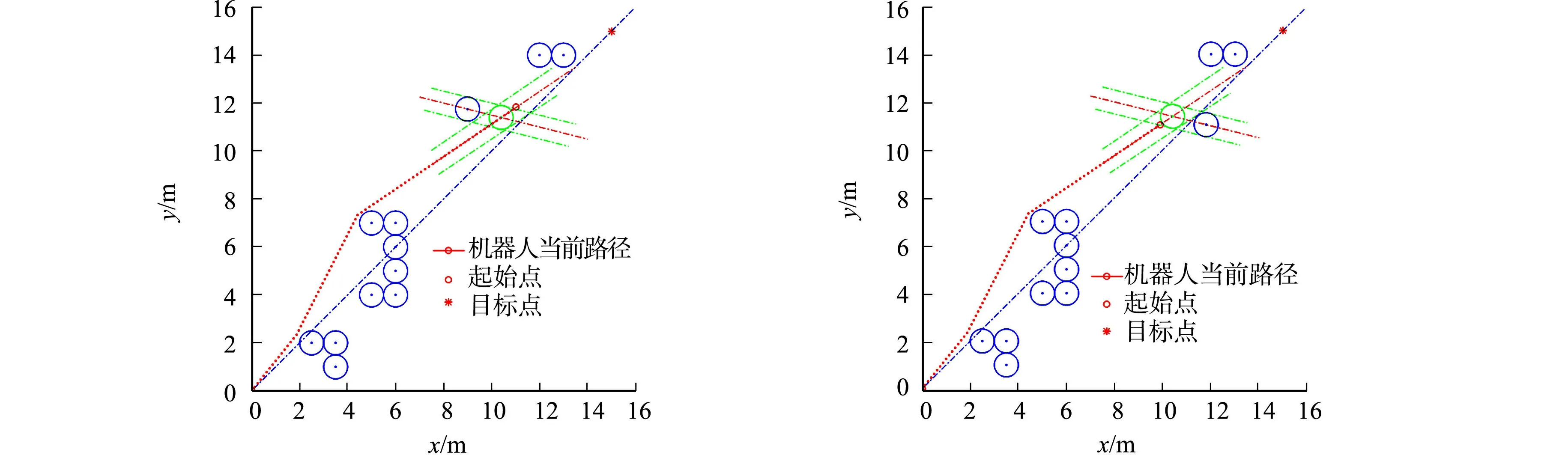
(a) 临界位置1 (b) 临界位置2

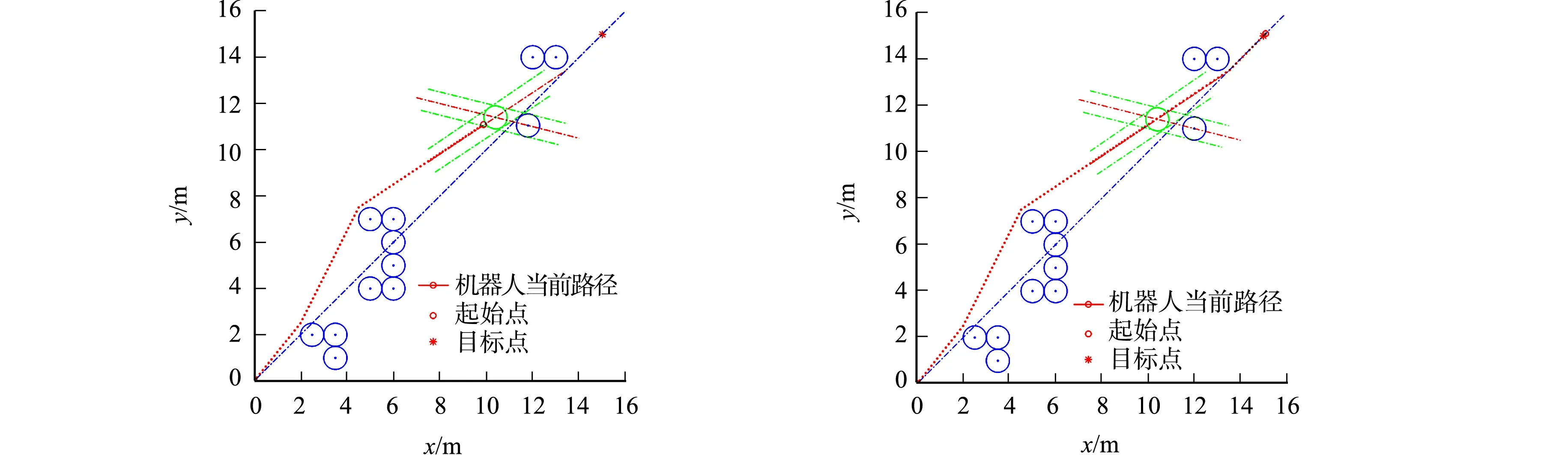
(c) 右范围减速 (d) 右范围全局-局部路径

(e) 左范围减速 (f) 左范围全局-局部路径

(g) 经典人工势场法 (h) 改进人工势场法 图13 局部路径规划示意图Fig.13 Schematic diagram of local path planning

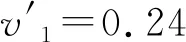
由图13(a)可知：当机器人运动到图中位置时，移动物体刚好运动到碰撞区.由图13(b)可知：当移动物体刚好运行出碰撞区时，机器人可以按照全局规划路径继续向前移动.

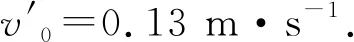
为了进一步验证文中方法的有效性，将文中方法与经典人工势场法和改进人工势场法[14]进行比较实验，经典人工势场法和改进人工势场法是目前已经成功应用于复杂环境下移动机器人路径规划的有效方法.经典人工势场法中机器人仅受障碍物的斥力和目标点的引力作用，机器人容易陷入局部极值，规划结果如图13(g)所示.图13(g)中：某几个时刻机器人和移动物体的运动方向、运行步长相同，导致机器人和移动物体同向运行一段距离，极大降低了路径规划的效率.改进人工势场法的实验结果，如图13(h)所示.改进人工势场法是在人工势场法的基础上，判断出机器人陷入局部极值时，增设子目标点使机器人摆脱局部极值，但该方法子目标点选择具有一定的盲目性，并且是障碍物陷入局部极值后才进行操作，在有移动物体的环境中甚至会出现路径震荡的现象，路径规划效率也较低.文中方法是在计算出移动物体的速度和运行方向后，提前减速或避开障碍物重新规划路径，可提高路径规划效率.

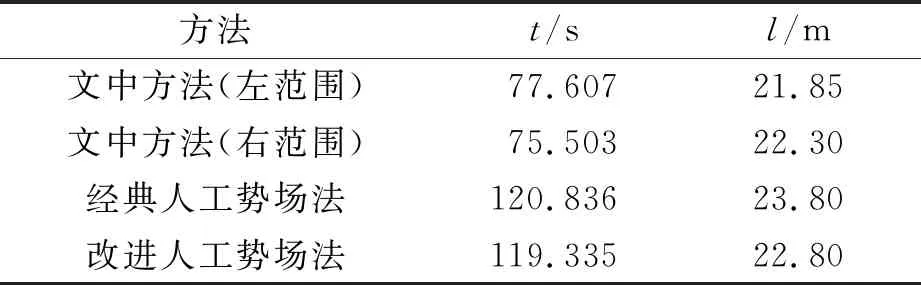
表1 不同方法的路径规划总时长与总长度的对比Tab.1 Comparison of total time and total length of different methods of path planning

文中方法与上述两种方法的路径规划任务的总时长和总长度的对比，如表1所示.表1中：t为整个路径总时长；l为整个路径总长度.由表1可知：在总时长和总长度两个方面，文中方法优于经典人工势场法和改进人工势场法，可提高整个路径规划任务的效率，因此，文中方法具有可行性和稳定性.此外，文中方法适用于匀速直线运动的情况，由于在正常情况下从某一起始点到某一目标点的行走遵循一定的习惯，即以一个最佳适应速度按照局部最短直线路径，向着目标点移动，这种运动行为可以近似为一系列匀速直线运动的组合.因此，文中方法在正常情况下均适用，但对于突发状况，如速度或方向上发生突变时，文中方法则不适用.

4 结束语

提出一种混合模式路径规划算法，使机器人能够在不同情况下确定通往目标点的最佳路径.在全局模式下，机器人利用事先存储的地图，进行环境建模，根据距离阈值对密集邻近的障碍物进行融合，形成一个整体，减少不必要的迂回循环路径，最终规划出全局路径.在局部模型下，对移动物体运用位置速度法分析运行路径，使机器人不仅在时间和距离上获得最佳路径，而且可以预判机器人可能被阻塞的情况，并选择避免此类情况的新路径，以当前位置为新的起始点向目标点重新规划出一条路径，如果在安全范围内探测到新的移动物体时，则继续进行局部规划.将文中方法与经典人工势场法和改进人工势场法进行比较实验，文中方法在机器人完成整个路径任务的总时长和总长度两个方面均获得较优的结果，因此，文中方法具有可行性和稳定性.