磁流变弹性体及其隔震(振)应用研究进展

雷 拓，郭绪新，刘伯权，王沁怡，孙向梅，邓煜生

(长安大学建筑工程学院，陕西西安 710061)

0 引 言

中国是地震频发国家，因地震造成的损失相当惨重，如唐山地震、汶川地震等。传统的抗震设计是基于保证结构具有足够的强度和延性来抵抗地震作用，该方法虽能实现结构“大震不倒”，但结构局部破坏在所难免且往往不易修复。隔震技术因其减震概念明确、技术成熟及减震效果显著而在工程中得到广泛应用[1]。然而，从结构振动控制方式看，目前的隔震技术仍属被动控制范畴，其减震效果直接与地震动特性相关。随着材料科学的发展，以智能材料为驱动的现代隔震技术为工程结构减震控制提供了新的思路。

磁流变材料因其能对外界磁激励做出响应而归为智能材料，包括磁流变液(Magnetorheological Fluid,MRF)[2-5]、磁流变弹性体(Magnetorheological Elastomer,MRE)[2,6-8]等。磁流变效应最早在20世纪40年代由Rabinow[5]发现。Shiga等[9]提出MRE的概念，MRE是将微米级磁性颗粒分散于固态基体材料中，在磁场作用下能够改变自身力学性能，且克服了MRF易沉降、稳定性差、环境污染等不足[10-12]。MRE基体材料主要有硅橡胶、天然橡胶、聚氨酯橡胶等高分子材料。在制备过程中对MRE施加磁场，使磁性颗粒取向的过程称为预结构化，经预结构化的MRE为各向异性材料，而无预结构化MRE则为各向同性，2种材料在力学性能方面差异较大。MRE具有可控性、可逆性以及响应速度快等特点，在医学[13]、汽车制造[14-15]、机械设备[16-19]等方面已有广泛应用。中国在磁流变材料及应用方面的研究起步较晚，但在一些高校及科研院所的努力下取得了一定成果[20-24]。在土木工程信息化、智能化的发展趋势下，MRE具有广阔的应用前景。本文综述了近年来MRE在隔震(振)应用方面的新进展，以期能够对土木工程领域MRE智能隔震方面的研究和应用提供参考。

1 MRE研究进展

1.1 MRE组成

MRE主要由基体材料、微米级的导磁性颗粒及辅助添加剂组成。

1.1.1 基体材料

硅橡胶较为柔软，在固化成型前黏度较低，有利于磁性颗粒在基体中均匀分散，或在磁场中形成有序的链状、簇状结构，如图1所示[25]。

聚氨酯橡胶因其较好的力学性能、较低的黏度及良好的热稳定性而备受关注[26]。天然橡胶等材料制备的MRE磁流变效应相对较低，部分学者研制了混合橡胶体系MRE。Zhang等[27]将磁流变液或磁流变胶注入MRE孔洞中，让MRE发挥“骨架作用”，结果表明混合型材料比原MRE具有更高的初始模量和磁流变效应。Hu等[28]通过调整聚氨酯与硅橡胶比例，使基体内部形成互穿结构，改善聚氨酯与硅橡胶的相容性，提高了磁流变效应。Zhang等[29]使用顺丁橡胶和天然橡胶制备不同混合比例的MRE，研究材料的耐久性问题，分析了耐久性与循环荷载和老化条件的关系。表1汇总了以不同基体材料制备的MRE。与硅橡胶相比，天然橡胶、顺丁橡胶等具有更好的弹性、力学性能，在土木工程领域更具有潜力。此外，还有学者利用废旧轮胎橡胶颗粒制备MRE，对MRE进行了物理表征，以探索其微观结构和磁性能，并进行了热分析[53]。Liao等[38]研究了γ辐射对MRE剪切模量的影响,结果表明，初始剪切模量和磁致剪切模量均随γ辐射的增大呈先增大后减小的趋势，辐射诱导的交联和降解反应影响MRE聚合物基体的剪切模量。基体材料作为磁性颗粒的载体，本身不具有磁性，但对磁流变效应具有显著影响。一般规律是，在较软的基体材料中，磁性粒子可发生较大位移，形成有序排列的颗粒链，并产生较大磁致模量；较硬基体材料对磁性颗粒的“禁锢”作用更强，其力学性能主要建立于基体材料之上，磁致性能相对较弱。

表1 不同基体材料制备的MRETab.1 MRE Prepared from Different Matrix Materials

1.1.2 磁性粒子

制备MRE的磁性粒子应具有高磁导率、高饱和磁化强度及低剩磁和低矫顽力的特点[54]。由表1可见，磁性颗粒多用微米级的羰基铁粉，除此之外还有铁粉、镍粉[55]等。Koo等[56]研究了含有4种硬磁性粒子(BaFe12O19,SrFe12O19,SmCo5,Nd2Fe14B)MRE在磁场下的位移响应，发现每一类型粒子产生的位移与磁场强度正线性相关。

Tian等[44]将包覆硅烷偶联剂的SrFe12O19纳米粒子掺入丁腈橡胶基体中，通过扫描电镜和X射线光谱对其进行表征，结果表明，SrFe12O19纳米粒子在橡胶基体中具有良好的分散性。Behrooz等[57]研究了氧化对MRE剪切模量的影响，结果表明，氧化作用主要影响基体材料，铁粒子经聚合物处理后有助于减小MRE剪切模量的损失。Padalka等[58]分别以Fe，Ni，Co合成的纳米线作为磁性填料，制备了硅橡胶基MRE，结果表明填充镍纳米线MRE的动态刚度最大，填充铁纳米线MRE的最小。粒子形状对MRE性能有显著影响，Hapipi等[59]比较了片状和球状羰基铁粉粒子的MRE性能，发现磁性颗粒含量相同时，MRE-P(片状羰基铁粉MRE)的初始模量高于MRE-S(球状羰基铁粉MRE)，但MRE-P相对磁流变效应却低于MRE-S。一方面由于MRE-P中基体与颗粒的相互作用较强，能量耗散小，初始模量较高；另一方面是MRE-P中磁性颗粒形成“纸牌屋”结构，这些链结构连接较弱，在较大应变时易于断裂。磁性颗粒粒径也会影响MRE的磁流变效应。Winger等[60]对4种不同粒径铁颗粒进行测试，显示磁流变效应对颗粒粒径有明显依赖性。通常认为，在一定的粒径范围内，磁流变效应随磁性粒子粒径的增大而增大。

磁性粒子是橡胶智能化的驱动材料。含有硬磁性粒子的MRE会形成磁极，类似于柔性永磁体，可用于执行器或驱动器。含羰基铁粉的MRE在隔震(振)器件中的效果更好，且高饱和磁化强度、低剩磁的粒子使得隔震(振)器件刚度变化更大，可调节范围更广。

1.1.3 辅助添加剂

除基体材料和磁粉外，添加剂也是制备MRE的重要成分。硅油加入硅橡胶中可使基体分子间间隙增大，分子间凝集减少。添加剂可提高基体的塑性和流动性，还可以平均材料内应力分布，使MRE具有稳定的材料性能[12]。

炭黑作为高温硫化型橡胶(如天然橡胶、丁腈橡胶、顺丁橡胶)的补强剂，可极大提高橡胶的机械性能和耐热性能，因其种类、粒径、结构等不同，硫化胶性能也有所差异。Rajhan等[39]研究了天然橡胶基MRE的拉伸强度、硬度、回弹率等与炭黑含量的关系。试验表明，硬度随炭黑含量的增加而增加，回弹率随炭黑含量的增加呈下降趋势。Chen等[61]通过试验发现MRE的零场模量和相对磁流变效应均随炭黑含量的增加而增加，阻尼比随炭黑含量的增加而减小，拉伸强度随炭黑含量增加而增大。炭黑含量(质量分数)从0%增加至7%时，抗拉强度提高了48.5%。

Aziz等[62]研究了不同类型多壁碳纳米管(Multiwall Carbon Nanotubes,MWCNT)对MRE形态、磁性和黏弹性的影响。结果表明，羧基化多壁碳纳米管(Carboxylated Multiwall Carbon Nanotubes,COOH-MWCNT)和羰基铁粉有较好的相容性，形成相互连接的网络，通过加入COOH-MWCNT，饱和磁化强度比原有MWCNT增加5%。同时还发现，环氧化棕榈油(Epoxidised Palm Oil,EPO)有助于分散MWCNT和羰基铁粉，增强磁流变效应。与传统MRE相比，添加COOH-MWCNT有助于提高MRE的初始模量、磁致模量和阻尼性能[63]。

1.1.4 MRE制备方法

因基体材料不同，MRE制备方法也有差异。研究人员尝试了多种MRE制备方法，包括人工模塑MRE[64]、真空辅助注射成型[65]。以室温硫化硅橡胶为基体材料的MRE一般制备方法如下：首先按设计比例将磁性颗粒、硅橡胶及其他添加剂混合均匀，再将混合物注入模具，放入真空箱排除混合物中气泡，最后混合物在室温下即可固化(硫化)。制备各向异性MRE时，需将试样放置在定向磁场中进行预结构化。与硅橡胶不同，天然橡胶、丁腈橡胶等需经过塑炼，将橡胶高分子剪切断链，降低分子量，以获得更好的可加工性和操作性，最后在硫化温度和压力下使橡胶线性高分子交联，形成网状高分子。

Bastola等[66]使用3D打印技术开发了一种混合型MRE，通过3D打印机将一定体积的MRF逐层封装至弹性体中，成品如图2所示。

在打印过程中会出现MRF不连续、形状和尺寸不易控制、层厚不稳定等问题。通过对不同材料流变性能的测定，发现挤出压力、初始高度和加料速度等打印参数对打印质量影响显著[67]。Bastola等[68]研究了MRF图形化和不同磁场方向对混合型MRE磁流变效应的影响，测试了挤压模式下混合型MRE的动态特性。Bastola等[69]进一步发现，3D打印MRE的磁流变效应与打印图案和外加磁场方向有关，表明3D打印具有制备各向异性或特殊结构MRE的潜力。将MRF分割成较小的点，可使磁流变效应保持一定的水平并减少磁性颗粒的沉降和MRF的渗漏。3D打印技术的应用，不仅实现了MRE制备方法的革新，也是对MRE材料结构上的创新。

1.2 MRE磁致力学性能

MRE力学性能在外部磁场作用下发生改变是其重要特征，如弹性模量、阻尼等，其中磁流变效应备受关注。相对磁流变效应反映了MRE在磁场下的变化能力，在实际工程应用中有重要意义。相对磁流变效应MR按下式定义

(1)

式中：Gmax为磁场作用下的最大剪切模量；G0为零磁场下的剪切模量。

影响MRE力学性能的自身因素主要有基体材料的种类、磁性粒子的含量、基体材料与磁性粒子界面的结合能力等。由表2可见，硅橡胶基MRE的剪切模量普遍低于天然橡胶或顺丁橡胶制成MRE的剪切模量。另外，磁性粒子含量越高，MRE的剪切模量越高[75,82]。

Davis[83]通过理论计算得出，剪切模量变化最大时，磁性颗粒最佳体积分数为27%。尹兵雪等[84]通过试验得出，有磁场下制备的MRE具有更高的磁致剪切模量和高磁流变效应。此外，添加剂对基体材料与磁性粒子的界面结合也有影响，合适的添加剂可使基体材料与磁性粒子有效结合，不仅提高MRE的剪切模量，还可提高磁流变效应[31,61,63]。

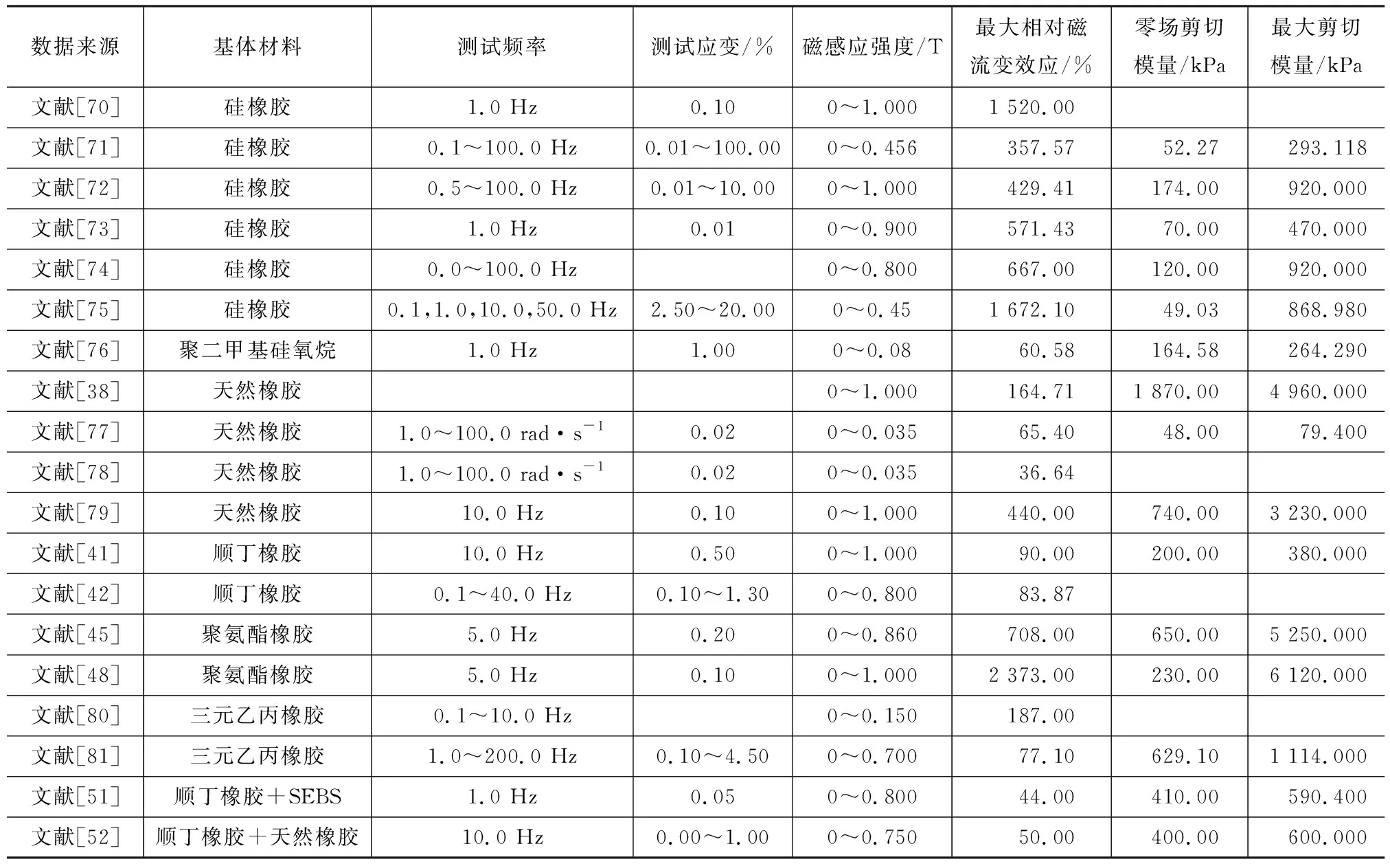
表2 MRE试验条件及磁流变效应Tab.2 Experimental Conditions of MRE and Magnetorheological Effect

MRE的磁致力学性能与相对磁流变效应存在一定的相互制约性，较高的相对磁流变效应往往基于较低的零场模量，但在工程应用中有较大的局限性。MRE虽解决了MRF的沉降问题，但也降低了磁场调控的灵活性。制备具有良好磁致力学性能和相对磁流变效应的MRE，需要在材料设计和研发方面开辟新思路。

MRE的剪切模量随磁通密度的增大而增大，当磁通密度达到600～800 mT时，磁流变效应达到平台期，即MRE进入磁饱和阶段，剪切模量不再增加。随着剪切应变的增加，存储模量与损耗模量均呈下降趋势[71-72,75]。这是由于基体中分子链断开，磁性粒子间的距离增大，引力减小，呈现出宏观的模量减小。存储模量、损耗模量均随激励频率的增加而增大，对频率有较强的依赖性[72,75]。

另外，研究人员通过损耗因子评估MRE的阻尼特性。MRE的阻尼DMRE为[85]

DMRE=DC+Dl+DM

(2)

式中：DC为基体阻尼；DI为界面阻尼；DM为磁力阻尼。

随着应变幅值增大，颗粒与基体材料之间的界面摩擦增大，由于颗粒与基体运动不同步，使颗粒与基体材料之间的弱物理键断裂。在磁场作用下，粒子间相互挤压，增加了粒子和基体之间的摩擦，从而消耗更多能量。颗粒与橡胶基体之间的强相互作用能减小滑动位移，使能量耗散减小，当磁场进一步增大时，损耗系数减小。这是因为在较强的磁场作用下，磁性颗粒之间相互作用，橡胶受到更大的约束，降低了橡胶分子的能量耗散，从而降低了损耗系数。随着磁通密度增大，MRE损耗因子呈现先增大后减小的趋势[72]。当磁场较低时，粒子间作用力增加了由界面滑移引起的能量耗散，对能量损失起关键作用；另外，基体与粒子的相互作用也较弱；在剪切应力作用下容易产生滑移能量耗散[74]。

1.3 MRE本构模型

1.3.1 磁偶极子模型

Jolly等[86]研究平行链中球形颗粒的磁力学特性，通过磁偶极子间能量相互作用关系，推导出小剪切应变γ(<0.1)下的磁致剪切模量G，即

(3)

式中：Φ为颗粒体积分数；Jp为单位颗粒体积磁偶极矩；μ0，μ1分别为真空磁导率和介质相对磁导率；d0为链中相邻颗粒中心距；d为颗粒直径。

Zhu等[87]分析了由柱状结构组成MRE的力学性能，考虑了颗粒所在链和相邻链的影响，建立体心四方结构模型对MRE的磁偶极子模型进行修正，计算了含有柱状结构MRE的磁致剪切模量ΔG，即

(4)

式中：τ为剪切应力；m为磁偶极矩；λ=D0/d0，D0为相邻链间距；R为球状颗粒半径；k，l，n分别为模型长、宽、高方向颗粒的数量。

结果表明，传统磁偶极子模型高估了MRE磁致剪切模量。从增加磁致剪切模量角度看，当颗粒体积分数较小时，链状结构比柱状结构表现更好，但当颗粒体积分数较大时，柱状结构更好。

Li等[88]提出了MRE双模态粒子链模型，即

(5)

式中：H0为磁场强度；s为小颗粒体积在颗粒总体积中的占比。

通过理论和试验研究了大颗粒与小颗粒混合制备MRE的力学模型和磁流变效应，计算表明s=23.2%时，磁致模量达到最大值，将试验结果与模型结果进行比较，发现模型结果准确地预测了大颗粒和小颗粒的最佳配比，但低估了MRE的磁致模量。

Ivaneyko等[89]提出了一个正则矩形晶格模型，即

(6)

考虑基体内部粒子的不同空间分布：各向同性分布(α=1)、链状分布(α<1)和平面片状分布(α>1)，研究了小变形、考虑磁致伸缩情况下，剪切模量与磁场的关系。Ivaneyko等[90]在文献[89]基础上进行了拓展，剪切模量随磁化强度的增大而增大，对磁颗粒的所有分布都具有相同的趋势，对剪切模量的预测与试验数据进行比较，两者有很好的一致性。

1.3.2 宏观力学模型

MRE是一种典型的黏弹性材料，实际应用中需建立数学模型对其复杂的力学行为进行表征，通过弹性元件和黏性元件的不同组合来反映应力-应变关系。Li等[91]提出了MRE四参数模型，即

τ=Gγ=(G1+iG2)γ

(7)

G1={(k1kb+k2kb+k1k2)[(k1+k2)2+c1ω2]+

(8)

(9)

式中：k1，k2，kb均为弹性元件刚度系数，kb反映模量对磁场的依赖性；c1为黏性元件黏度系数；ω1为激励频率。

通过MATLAB优化算法对不同工况下4个参数进行了识别。经试验与模型预测结果比较可知，四参数黏弹性模型在10%应变内能较好地预测MRE性能。

王奇等[92]考虑MRE的松弛行为，建立了五参数广义Maxwell模型，总结了模量与参数和时间t的函数关系，即

(10)

式中：k3为弹性元件的刚度系数；c2为黏性元件的黏度系数。

Chen等[93]采用流变模型来研究MRE动态力学行为，推导了流变模型的本构关系，通过模拟具有多种内在特性和受外部激励的MRE特性，验证了该模型的有效性。朱俊涛等[94]根据MRE基体黏弹性行为和磁致模量的变化，引入黏弹性分数阶导数模型(VFD)，给出了MRE磁参数模型的复数模量Y(ω)，即

Y1(ω)+iY2(ω)

(11)

(12)

(13)

式中：Y1(ω)，Y2(ω)分别为存储模量和损耗模量；σ(ω)为应力；ε(ω)为应变；ω为角频率；Em为非线性弹簧元件的磁致模量；E0为弹簧元件的弹性模量；T为VFD元件中表征特征时间的参数；β为分数阶导数；iβ=cos(βπ/2)+isin(βπ/2)，β∈(0,1)。

分析了MRE磁参数模型复数模量、力学损耗等动态特性与频率、外加磁场及分数阶导数的关系，结果表明，采用VFD模型能够在较宽频率范围内较好地模拟试验性能。

Guo等[95]建立了基于分数阶的参数化本构模型，MRE的Y(ω)为

(14)

在耦合场基础上，提出了一种在压应力作用下的颗粒链剪切模型，用于研究MRE的磁流变效应，即

(15)

式中：χ为颗粒磁化率；k0=d0/R；当颗粒足够多时A≈1.202；εmatrix为基体压缩应变；η为Abel黏壶的黏度系数。

当颗粒体积分数较小时，建立的模型与试验数据吻合较好，该模型能较好地描述MRE的动态模量与频率和变化磁场的关系；当Φ=46%时，拟合结果与试验结果的差距变大。文献[94]，[95]虽都采用分数阶的参数化模型，但二者的模型建立方式不同。

Eem等[96]提出一种结合Rambere-Osgood模型和Maxwell模型的动态模型，用来描述MRE的力和位移关系。式(16)为Rambere-Osgood模型的表达式，式(17)为模型卸载情况。

(16)

(17)

式中：FR为加载力；x为位移；K0为剪切刚度；Fy为屈服力；Fi，xi分别为加载、卸载转换点时的力和位移；r为黏弹比例，r由滞回环形状决定。

进而可得Maxwell模型

(18)

F=FR+FM

(19)

式中：FM为作用在Maxwell模型上的力。

通过试验和模型仿真结果比较，较好地描述MRE的力-位移关系，验证了所提动态模型的有效性。

由于MRE应用时磁力耦合的复杂性，本构模型仍需深入研究。MRE在磁、力共同作用下，磁性粒子位置、相互作用力的变化非常复杂，MRE的材料、制备方法的差异导致试验结果的离散性较大，也使MRE本构模型研究难度增加。此外，还需在试验基础上，通过微观模型揭示MRE内部结构在外界磁场下的流变机理和主要影响因素，进一步建立合理的宏观力学模型和参数表征MRE宏观力学行为。显然，MRE本构模型研究是MRE器件产品开发应用的基础。

2 MRE隔震(振)应用研究进展

2.1 MRE隔震(振)应用类型

目前，多数MRE隔震支座是基于传统叠层橡胶支座研发的，将MRE片(块)与钢板结合形成叠层结构，该结构形式可使隔震支座在发生较大水平位移时，能够承担较大竖向荷载。Wahab等[97]制作了天然橡胶基MRE全尺寸隔震支座，如图3(a)所示。Li等[98]设计了大容量叠层MRE隔震装置，如图3(b)所示，并在振动台上进行试验，以评估该装置的性能，其竖向荷载超过2 744 N，最大为3 626 N。Yarra等[99]制作了基于MRE的高速公路桥自适应隔震支座，每个支座配有4组叠层MRE-钢板，有8个电磁铁，电磁铁形成闭环磁场，如图3(c)所示，评估了支座在不同磁场、剪切应变、激励频率下的性能。Gu等[100]提出智能基础隔震策略，通过3层建筑模型，比较了地震激励下不同隔震方案的有效性，结果表明被动隔震系统性能有限，智能隔震策略的适用性得到试验验证，MRE隔震支座如图3(d)所示。

MRE-钢板叠层结构隔震(振)支座能够有效隔离水平方向振动，但给隔震(振)支座设计带来挑战。线圈外置式设计将MRE-钢板叠层结构置于线圈内部，如图4(a)所示。该设计可为MRE提供较为稳定的匀强磁场，外侧钢轭一方面可使隔震(振)支座形成完整磁路，减小磁损耗，另一方面可为电磁线圈和叠层结构提供保护作用，但该线圈布置形式在工作时产生的热量不易散除，对MRE性能有一定影响。此外，考虑到隔震(振)支座在极限工况下水平变形的要求，线圈和外侧钢轭与叠层结构要留有一定安全距离，因此隔震(振)支座直径较大。线圈端部式设计如图4(b)所示，线圈位于MRE-钢板叠层结构的端部，该设计为保证足够磁场强度，通常会在叠层结构两端布置线圈，或布置多组MRE-钢板叠层结构形成闭合磁路，如图3(c)所示。Sun等[101]通过软件模拟发现多组MRE-钢板叠层结构中的磁通密度要高于单组MRE-钢板叠层结构，线圈端部设计有利于减小隔震(振)支座直径，但需要考虑磁路的完整性。

除了典型的叠层MRE隔震支座外，还有按剪-压工作模式设计的隔振器。隔振器水平刚度调节范围较大，但由于重力作用，存在竖向预应变，导致竖向刚度调节范围变小，限制了其应用范围[102]。Yang等[102]提出了MRE剪切-压缩混合模式，在混合MRE隔振器中嵌入2个MRE块，一个用于剪切模式，另一个用于压缩模式，如图5(a)所示。Leng等[103]也研发了混合模式MRE隔振器，如图5(b)所示，并对其进行试验测试，通过数值模拟验证该装置能有效减轻波浪荷载对海洋结构工程的振动。剪-压模式隔振器能够对水平和竖直2个方向的振动进行控制，但各方向的变形控制范围均有所限制。因此，该类型隔振器尚有优化空间，若各MRE能够受独立电磁线圈控制且互不影响，则MRE可调控范围能得到较大改善。

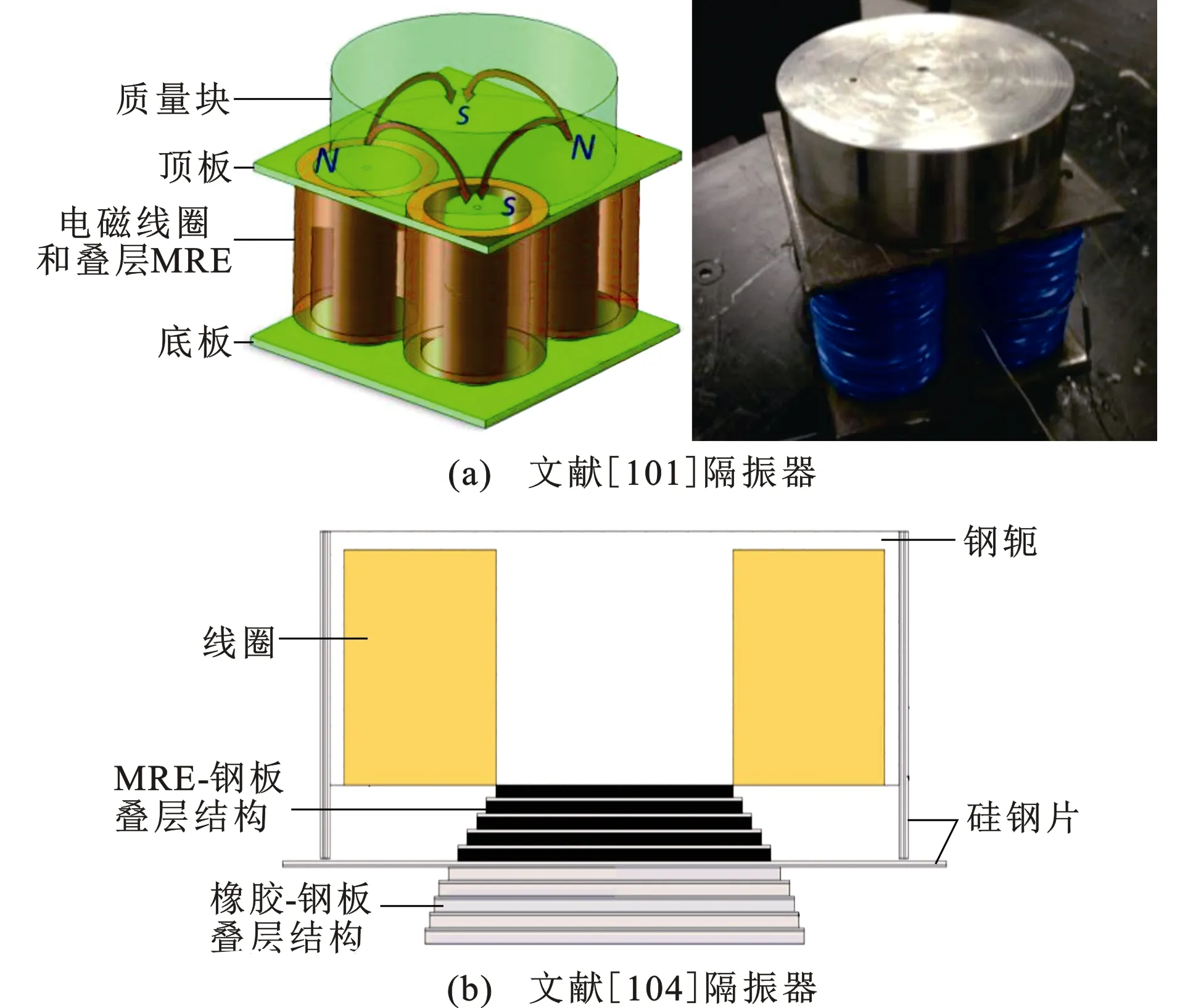
Sun等[101]研究并评估了一种半主动调谐质量阻尼器，该阻尼器由4组MRE-钢板叠层结构组成，4组叠层结构形成正方形，用于调节刚度，如图6(a)所示。该设计不仅增加了调谐质量阻尼器的稳定性，而且消除了设计中的磁路间隙。Wang等[104]提出了一种基于锥形MRE隔振器的变刚度调谐质量阻尼器系统，介绍了锥形隔振器的设计，并与传统圆柱形隔振器进行了比较。在此基础上，制作了MRE调谐质量阻尼器，如图6(b)所示，在谐波荷载作用下进行试验。结果表明，该MRE调谐质量阻尼器系统能有效控制结构振动。

2.2 MRE隔震(振)支座试验研究

研究人员对MRE隔震(振)支座的试验可分为以下2类。

第一类试验是对隔震(振)支座性能进行测试，测试条件及隔震(振)支座的刚度、阻尼变化情况如表3所示。从试验结果看，当隔震(振)支座通电后，刚度和阻尼发生明显变化，说明MRE发挥作用。Xing等[107]所做试验中，隔震支座的刚度、阻尼变化特别突出，究其原因，一是制备MRE的磁性颗粒含量较高，通入电流较大所得磁场较高；二是激励频率较大，MRE剪切模量与频率呈正相关。Li等[98]在试验中发现，隔震支座的磁场强度远未达到MRE磁饱和场强，其主要原因是隔震支座存在空气间隙导致漏磁和MRE与钢板黏结较差、存在气泡等。Yarra等[99]进行了隔震支座破坏形式的试验，结果表明该支座破坏是因为MRE与钢板的黏结失效，这与文献[98]情况相似。

第二类试验是将MRE隔震(振)支座安置在缩尺框架模型中，在振动台上输入地震激励，并通过相应控制算法来实现对隔震(振)支座的智能控制，试验情况如表4所示。从采用的控制算法看，模糊逻辑控制可以提供一个简单且稳健的框架来指定非线性控制，以适应不确定性和不精确性[115-116]。此外，模糊控制器不依赖于数学模型的分析过程，与经典控制理论相比，模糊控制器更容易处理来自外部荷载和结构响应的不确定性[111]。Gu等[114]使用2种控制算法对4种地震波(按震级的20%输入)进行了比较，结果发现遗传算法(Genetic Algorithm,GA)优化的模糊逻辑控制明显优于基于广义回归神经网络(General Regression Neural Network,GRNN)逆模型LQ调节器(LQR)控制，表明模糊逻辑控制算法可以更好地应对MRE隔震支座控制系统的高非线性、滞后性。Gu等[100]使用滑模控制(SMC)衍生的Bang-Bang控制作为基准控制算法进行试验。Bang-Bang控制系统能较好地限制底层位移，但在El Centro和Northridge地震波下，Bang-Bang控制系统的层间位移明显大于被动控制系统的隔震支座。Chen等[113]为解决结构控制系统的时滞问题，提出了一种双循环自适应控制器。内循环用来补偿MR器件引起的响应时间延迟，外循环则采用一个类似李雅普诺夫函数的自适应控制算法。该算法使结构位移主要控制在隔震系统中，而上部结构仅有少量层间位移，实现了上部结构近似刚体的平动，结果表明新型双循环控制策略能够提供令人满意的性能，减轻建筑物和其他结构由于地震引起的结构振动。通过试验对比发现，有源控制的结构响应明显低于无源被动控制，有源控制隔震支座的隔震效果更优。各控制算法所优化控制的目标量不同，同时考虑到隔震支座的设计、试验装置不同，隔震效果差异较大。进一步对比文献[100]和文献[114]，Bang-Bang控制对于底层位移的控制要优于LQR控制和模糊逻辑控制，但对于相对位移，模糊逻辑控制算法更优。

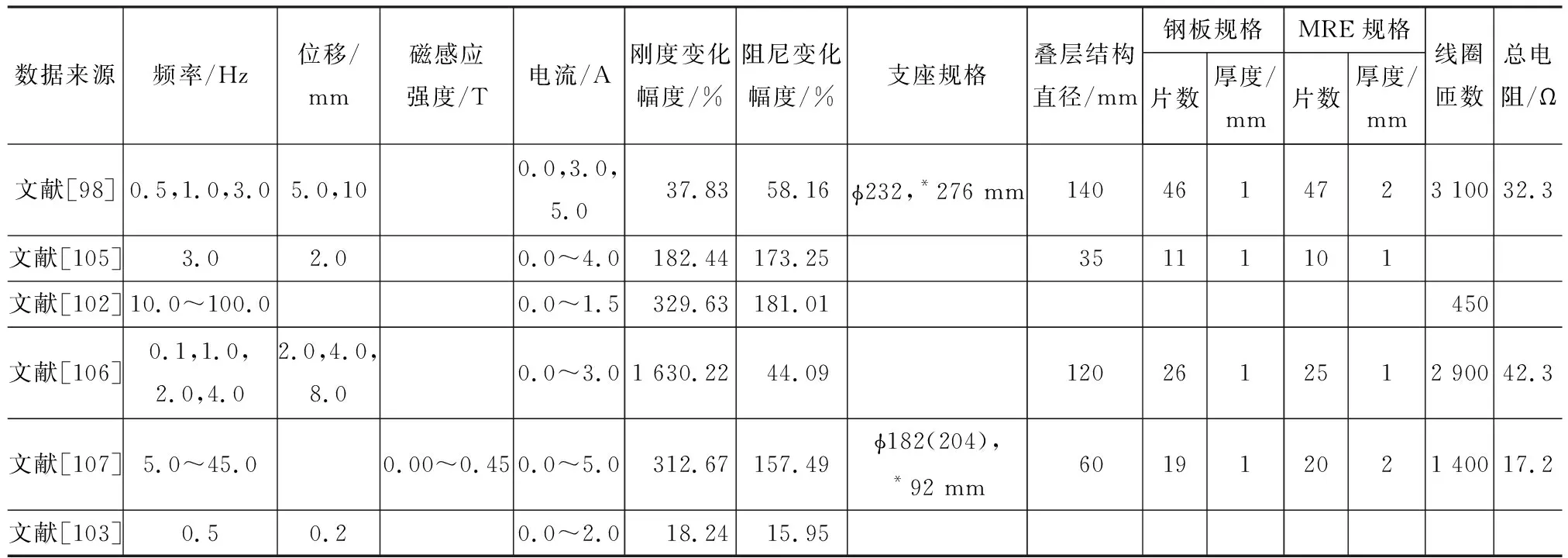
表3 MRE隔震(振)支座试验条件及性能Tab.3 Experimental Conditions and Properties of MRE Isolation Bearing

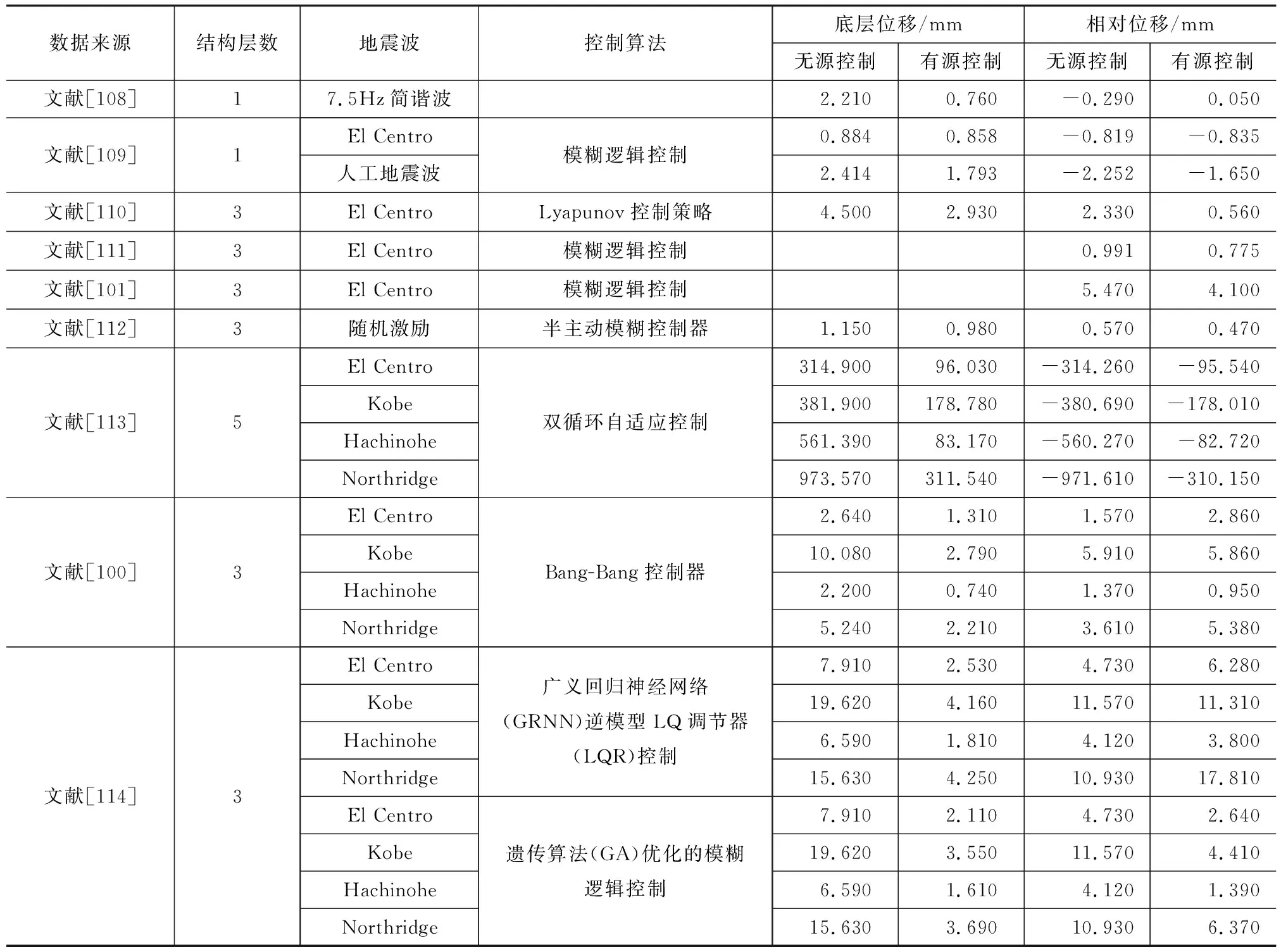
表4 MRE隔震(振)支座隔震(振)性能试验Tab.4 Isolation Performance Test of MRE Isolation Bearing

2.3 MRE隔震(振)支座力学模型

为了模拟隔震(振)支座的动力性能，研究人员建立了不同的力学模型，如表5所示。Bouc-Wen模型是一种经典的迟滞模型，可用于修正MRE隔震(振)器的性能，Yang等[117]提出了唯象学模型，该模型是由Bouc-Wen模型与Voigt模型并联组成，用来描述MRE隔震支座的磁致阻尼、刚度变化。试验证明，该模型预测隔震支座的力-位移关系与电流恒定时的试验测量数据相吻合。MRE隔震支座与传统叠层橡胶支座相似，而当剪切变形超过临界剪切应变时，自适应隔振器会出现应变硬化现象。为此，Li等[118]提出了一种新的模型，在该模型中，上支路为标准三参数实体模型，下支路为修正的Maxwell模型，包含一个应变硬化弹簧单元和一个阻尼单元串联。结果表明，该模型能较好地描述自适应隔震支座力-位移、力-速度滞回行为，当剪切变形超过临界应变时，该模型可描述隔震支座的应变硬化现象。Nguyen等[112]为了描述MRE在剪切方向变形的动力学特性，建立了动力学模型，并将模型及相关仿真结果与谐波激励下的试验结果进行比较。结果表明，大多数情况下，模型适应度高于90%，平均适应度约为93%。在频率3～30 Hz、剪切应变6%～14%的范围内，MRE模型可以很好地工作，但在低频、小幅值激励情况下，模型预测结果不够精确。

3 结 语

(1)MRE经过多年发展，日益成熟，基体材料可根据磁致力学性能、相对磁流变效应等因素综合考虑，磁性粒子根据功能化需求选择软磁性粒子或硬磁性粒子。基体材料、磁性粒子种类繁多，各有优劣，需结合具体应用环境选择合适配方。MRE在制备、测试等方面尚未建立起统一标准，不同测试方法导致数据差异较大，无法直接比较。现阶段鲜有能投入土木工程领域进行应用的MRE，天然橡胶基MRE具有较好的力学性能，但还需提高相对磁流变效应，才能有效扩大隔震(振)支座刚度变化范围。对于材料制备，可结合新兴技术，如3D打印等，从MRE结构、制备方法进行革新，解决MRE力学性能和相对磁流变效应相互影响的问题，使MRE能够广泛应用。

表5 MRE隔震(振)支座力学模型Tab.5 Mechanical Models of MRE Isolation Bearing

(2)基于磁偶极子的力学模型经不断完善，从仅考虑单一链模型发展至考虑多链相互作用、不同链形态的影响，但模型均引入大量假设，而实际颗粒分布更为复杂。宏观上，MRE的性态和弹性体相似，但在磁场作用下，磁性粒子的相互作用、基体材料与磁性粒子的相互作用使得MRE力学行为变得复杂。可通过先进技术如CT、电镜扫描等，结合多尺度MRE计算模型，经试验数据校验，完善MRE本构模型。

(3)MRE智能隔震(振)支座的研发取得了一定进展，已设计出多种用于土木工程领域的智能隔震支座，但还需进一步优化设计。隔震(振)支座在承受较大竖向荷载同时还需满足较大剪切变形，而现有试验中的应变鲜有超过10%，并且钢板与MRE存在黏结失效的问题。隔震(振)支座在极限使用状态下须保证能输出稳定磁场，不断优化磁路，合理控制器件尺寸以满足工程需要；同时，还需减小电磁线圈发热对MRE性能的影响，综合考虑各种因素优化智能隔震(振)支座的结构设计。

(4)控制算法是控制智能隔震(振)支座的“中枢大脑”。通过试验发现，经历相同地震动时，不同算法得到的结构响应存在差异。因此，还需不断优化算法、深度学习，以适应不同类型地震动。控制算法的混合使用也是一个发展方向，但要考虑算法复杂化带来“时滞”的不利影响，在实现控制要求的同时，应尽量简化。