开洞对RC框架填充墙平面外受力性能的影响

杨春侠，吴艳谋，梅 艺，蒋耀华，徐凌浩

(1. 长沙理工大学土木工程学院,湖南长沙 410114；2. 中机国际工程设计研究院有限责任公司，湖南长沙 410007)

0 引 言

在现实生活之中为了满足建筑的使用要求，通常会在框架填充墙纵墙上开设门洞和窗洞。由于填充墙开洞的存在，填充墙开洞的四角是裂缝出现的薄弱位置，在平面外位移作用和平面内剪切作用下，开洞墙体四角容易出现向四周发散的裂缝。张荣[1]通过有限元计算分析,初步探讨了开洞位置对墙体刚度的影响,并建议对现有开洞墙抗侧刚度计算方法进行修正。吴会阁等[2]运用ABAQUS有限元分析软件对设窗洞的蒸压加气混凝土砌块砌体承重墙进行了非线性分析，研究表明增大开洞水平尺寸导致极限承载力明显降低，而对相应位移的影响则小得多。

对于开设开洞的填充墙框架结构，在平面内荷载作用下的研究已经比较成熟，但是对于开洞率、开洞数量、开洞位置、开洞形状、墙体高宽比、墙体高厚比等影响因素在平面外位移作用下的分析还不够完善。本文建立不同开洞率、开洞位置、开洞形状的RC框架填充墙模型，根据填充墙的等效应力云图和等效塑性应变云图，对模型的受力情况和填充墙的破坏形式进行详细分析，总结了开洞对填充墙平面外单调加载的影响。

1 框架填充墙有限元模型建立

1.1 有限元模型的选取

1.1.1 钢筋混凝土模型

本文在分析中考虑到钢筋是一种细长的轴向受力构件，故采用桁架单元来模拟钢筋的轴向力学性能。由于本文重点研究的是框架填充墙的平面外受力性能，对于钢筋和混凝土的相互作用不做重点分析，因此在后续的分析当中，假定钢筋和混凝土不产生相对滑移。利用ABAQUS“相互作用”功能模块中的嵌入指令，将钢筋单元嵌入到混凝土单元内部，用混凝土主单元来约束嵌入钢筋单元的节点平移自由度。

1.1.2 砌体填充墙模型

整体式模型是忽略砂浆和块体之间界面的力学行为，将砌体看成单一均匀连续的材料来建立模型。通过一个本构关系来表达其力学性能，由于已有大量试验进行了验证，整体式模型进行模拟论证的文献也很丰富，整体式建模方法比较成熟，因此，本文采用整体式模型对砌体填充墙进行模拟。

1.2 单元类型的选取

1.2.1 混凝土单元

本文主要是分析构件的受弯问题，因8节点可以较好地承受扭曲变形，减少自由度，能够节省计算的时间，并且能够获得较为精确的结果，所以本文对混凝土的模拟采用二次缩减积分单元C3D8R。

1.2.2 钢筋单元

桁架单元用于只承受拉伸和压缩作用而不能承受弯矩作用的杆件。本文不考虑其横向抗剪作用及自身的抗弯能力，因此采用桁架单元来模拟钢筋。

1.2.3 砌体填充墙单元

本文对砌体填充墙建立整体式模型，将砌体填充墙看作一种连续均质的材料，因为砌体和混凝土的力学性能类似，受压强度高，受拉强度低，并且存在明显的脆性，所以本文参照混凝土选取二次缩减积分单元C3D8R来模拟砌体填充墙。

1.3 材料本构关系

1.3.1 混凝土本构关系的选取

刚度恢复系数ω分为受压刚度恢复系数ωc和受拉刚度恢复系数ωt，用来模拟混凝土拉、压作用相互转化时的刚度恢复。本文ωc=1,ωt=0,这表明混凝土从受压变成受拉时刚度不能恢复，而从受拉变成受压时刚度可全部恢复。结合材料的本构关系方程可以算得材料在受拉和受压时的损伤因子d。损伤因子d取值在0～1之间，越接近1表明结构损伤越严重，考虑到计算条件，本文损伤因子最大取值为0.95。

本文使用规范[3]附录C中的混凝土单轴受压本构关系，其表达式如式(1)所示

(1)

式中：ac为混凝土单轴受压本构关系曲线下降段参数；fc,r为混凝土单轴抗压强度代表值；εc,r为与单轴抗压强度fc,r相对应的混凝土峰值压应变；Ec为混凝土的弹性模量；ε为应变；σ为应力。

使用规范[3]附录C中的混凝土单轴受拉本构关系，其表达式如式(2)所示

(2)

式中：at为混凝土单轴受拉本构关系曲线下降段的参数。

1.3.2 砌体本构关系的选取

本文采用整体式方法建立砌体填充墙有限元模型，在模型建立时只需将墙建立成一个单一均质连续的整体墙板。由于砌体墙板和混凝土具有相似的材料性能，因此在对砌体墙板进行属性定义时仍然使用混凝土塑性损伤模型去分析，本文砌体填充墙选用文献[4]的砌体本构关系，参考《砌体结构理论与设计》[5]。

1.3.3 钢筋本构关系的选取

因为考虑包辛格效应的钢筋本构模型不易采用公式表达，所以本文选用二折线钢筋本构模型。在钢筋达到屈服点之前将钢筋看作线弹性材料，而在达到屈服点之后则看作完全塑性材料。

1.4 平面外受力RC框架填充墙模型的建立

构件参照文献[6]的试验进行装配，有限元分析的加载制度参照试验，试验加载至完全冲击破坏，在有限元分析时，平面外单调递增荷载最高加载至50 kN。

网格划分的方法参照平面内分析模型，将混凝土框架、砌体填充墙统一划分为六面体网格，全局尺寸为0.1；钢筋采用桁架单元划分。通过以上步骤建立好的框架填充墙模型及其网格划分如图1所示。

1.5 RC框架填充墙平面外受力结果拟合

对于平面外模型的拟合，参考文献[6]的填充墙平面外加载试验。本文选用其中的K-Q1墙片进行ABAQUS有限元模拟，对比其试验结果，验证本文平面外模型的正确性。

试验中当试件加载至13 kN时，位移为1.712 mm，裂缝开始出现在填充墙背立面的中轴线位置，由顶层砌块的灰缝垂直向下发展；随着荷载的不断增加，填充墙的正立面上出现了2条斜裂缝，由墙柱的连接处斜向向下发展，随着荷载的不断增加，斜裂缝发展到墙体底部。试验裂缝的发展见图2。当荷载增加至41.4 kN时，位移为34.695 mm，填充墙由于平面外的局部承载能力不足，加载处的四周墙体出现大面积的破坏[7-8]。填充墙破坏时，框架完好，墙体与框架柱之间的刚性连接基本完好。

在模拟中由于砌体的平面外破坏主要以受拉为主，因此采用Mises准则进行判别，当模型某一点的应力达到材料的极限应力值时，则可判断材料失效破坏。填充墙的应力及位移云图见图3。

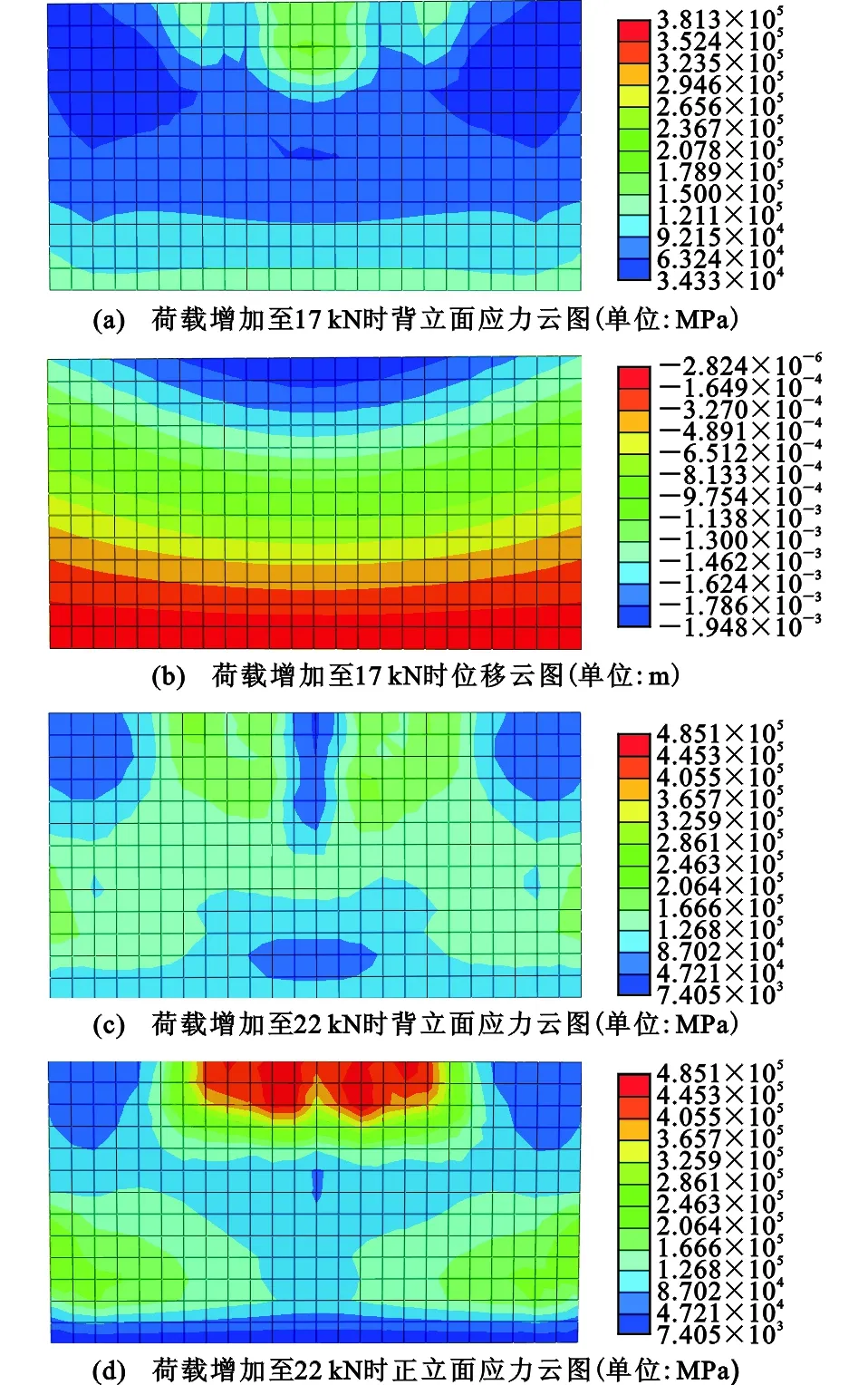
当荷载为17 kN，此时墙体的加载处位移为1.948 mm，填充墙背立面出现最大应力；当荷载增加至22 kN时，填充墙背立面中轴线处的垂直裂缝向下发展，并且在其两边分别出现2条裂缝，并随着荷载的增加向下发展。在填充墙的正立面，墙柱连接处出现了2条斜裂缝；当荷载增加至42 kN时，填充墙加载处的位移达到34.85 mm。

通过对平面外试验的数值模拟和对拟合结果的分析可知[9-10]，平面外墙体的建模方式、本构参数、边界约束等都是可行的，分析得出的结果与试验结果差别不大，数值模拟得到的开裂荷载和极限荷载相比于试验数值稍微偏大。试验的挠度曲线和数值模拟的挠度曲线见图4，有少量的误差，总结为如下几点原因[11]：①在模型建立时，本文采用的是整体式模型，跟实际情况有一定的差别；②人为因素的存在，可能导致试验模型的强度偏低；③试验中加载后期挠度曲线斜率有轻微增长而数值模拟没有出现，这是因为在试验中填充墙破坏后出现了一定的拱效应，而在模拟时无法模拟填充墙真实裂缝的发展而无法产生拱效应。

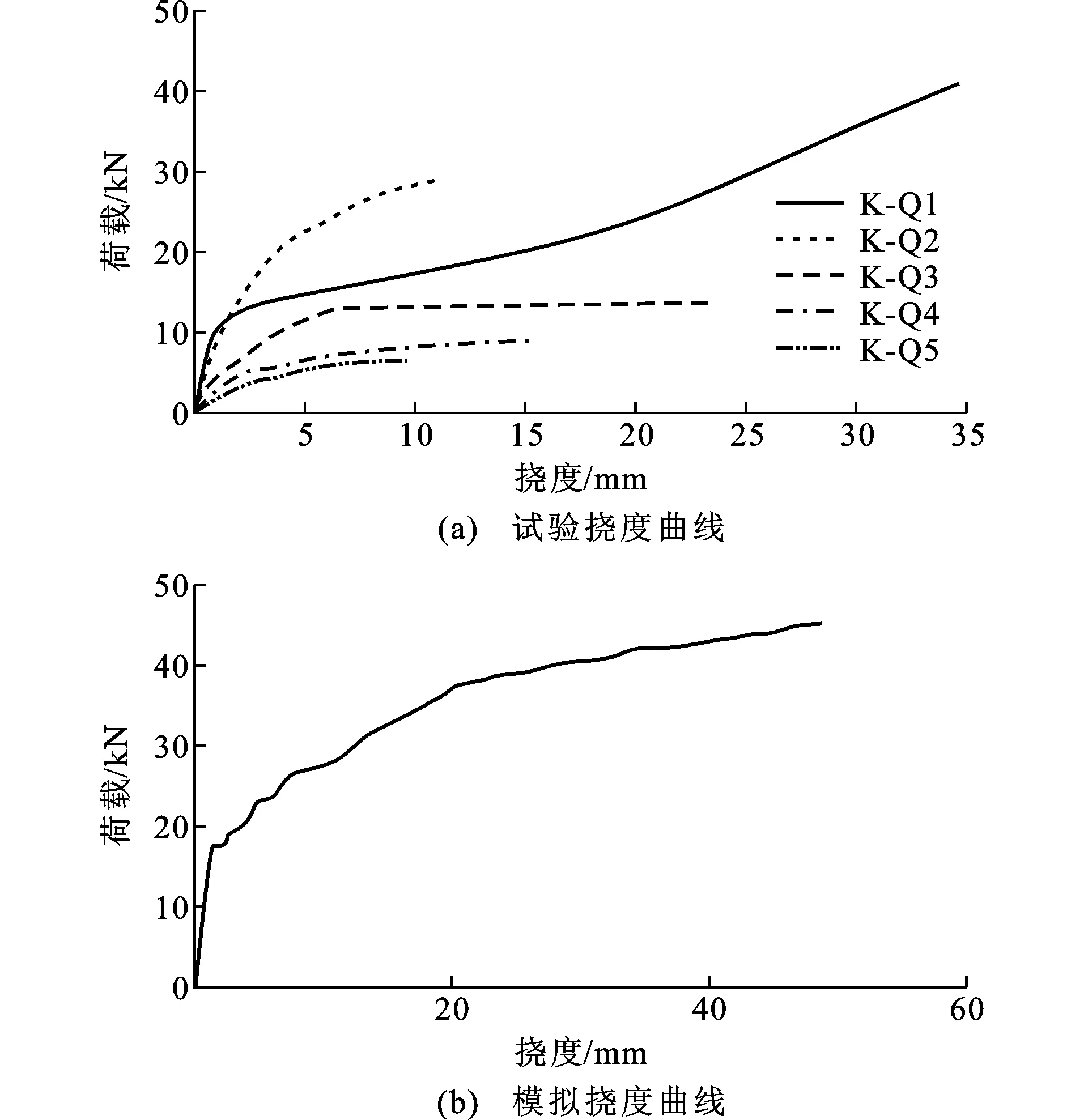
采用所建模型对框架填充墙的试验墙体破坏全过程进行模拟，验证了所建模型的可靠性[12]。对文献[6]中框架填充墙试验模型的开裂荷载、极限位移、挠度曲线等重要参数进行了拟合。对结构的裂缝发展与分布做了全过程的拟合，结果比较理想，验证了本文建立模型的可行性及参数选取的正确性。

2 开洞率对RC框架填充墙平面外单调加载的影响

2.1 不同开洞率的填充墙应力云图分析

分别建立开洞率为10%，20%，30%，40%的中心开洞框架填充墙模型，并进行平面外受力性能分析，详细的开洞尺寸及开洞率见表1，框架尺寸为2 250 mm×1 375 mm，对不同开洞率的框架填充墙进行平面外位移作用下的应力分析[13]。由于有限元模拟涉及到的云图较多，故本文仅对部分云图进行分析。

当平面外层间位移角达到1/1 000时，在此循环中每个模型都出现了不同程度的应力集中现象，在填充墙两底角的边界处每个模型都出现了应力集中，并且应力大小已达到材料的极限受拉值。与KD1模型不同的是KD2，KD3，KD4模型在两侧出现的应力集中区域较大，而且都在开洞下侧出现了不同程度的应力集中。其中KD2的应力集中区域最大，几乎包含了整个开洞下方的区域，而且KD2在开洞下方的应力值最大；KD3应力集中区域相对较小，覆盖开洞正下方1/3的区域，其应力值相比于前者较小；KD4开洞正下方应力集中区域最小，其应力值也是最小。

当平面外层间位移角达到1/700时，在此循环中每个模型都出现了不同程度的应力下降，而且在两侧底角边界应力集中的区域出现了明显的上移。KD1的应力集中区域也开始向开洞下方发展，KD1和KD2在上一步加载中的应力集中区域出现了应力下降，相比之下KD3的应力下降较为缓慢；KD4的应力集中区域出现了小幅度的上移。

表1 不同开洞率的框架填充墙模型Tab.1 Frame Filled Wall Models with Different Opening Ratios

当平面外层间位移角达到1/500时，相比于上一个加载循环，所有模型的应力下降区域都产生了明显的扩大。KD1中边界处的应力下降区域明显增大，应力集中区域向开洞方向发展；KD2和KD4中边界处的应力也出现了明显的下降，同时在填充墙中下方1/4处出现了明显的横向应力下降区段；KD3的边界没有出现明显的应力下降区域，其他2个模型一样，也出现了明显的横向应力下降段。

当平面外层间位移角达到1/300时，每个模型的边界处都出现了不同程度的应力下降。KD1的边界应力下降区域迅速扩大，出现了水平下降区段，应力在开洞下方集中；KD2，KD3，KD4的边界下降区域都出现了小幅增长，应力集中区域小幅上移，应力大小没有明显的变化。

当平面外层间位移角达到1/200时，填充墙两侧中部边界处都出现了明显的应力下降区域，其中KD4边界处应力下降区域面积最大。

当平面外层间位移角达到1/150时，模型墙体都出现了大面积的应力下降区域。KD1和KD4在填充墙中部出现了水平应力下降段；KD2和KD3在填充墙中部有出现水平应力下降段的趋势。

通过以上的云图分析，对框架填充墙的纵墙平面外破坏特征点进行了总结，对应的位移角见表2。

通过对每一级加载情况的分析可以看出：在加载初期KD2和KD3的应力发展十分迅速，首先出现明显的水平应力下降段，而KD1和KD4的应力发展相对缓慢；加载中后期KD1和KD4的应力发展十分迅速，先于KD2和KD3出现2条贯通的水平应力下降段；KD2出现边界开裂和水平横缝的位移角都相对较小。通过以上分析可以判断开洞率对模型初裂时的位移角没有太大的影响；开洞率越大的模型，边界开裂时的位移角越大，其出现水平横缝时的位移角越小。

表2 墙体平面外破坏特征点的位移角1Tab.2 Displacement Angle 1 of Failure Feature Points Outside Wall Plane

2.2 不同开洞率的填充墙等效塑性应变云图分析

分别选取层间位移角为1/700，1/200，1/100，1/65，1/35，1/25时的应变云图对墙体破坏形式进行分析[14-15]。层间位移角为1/25的等效塑性应变云图如图6所示。

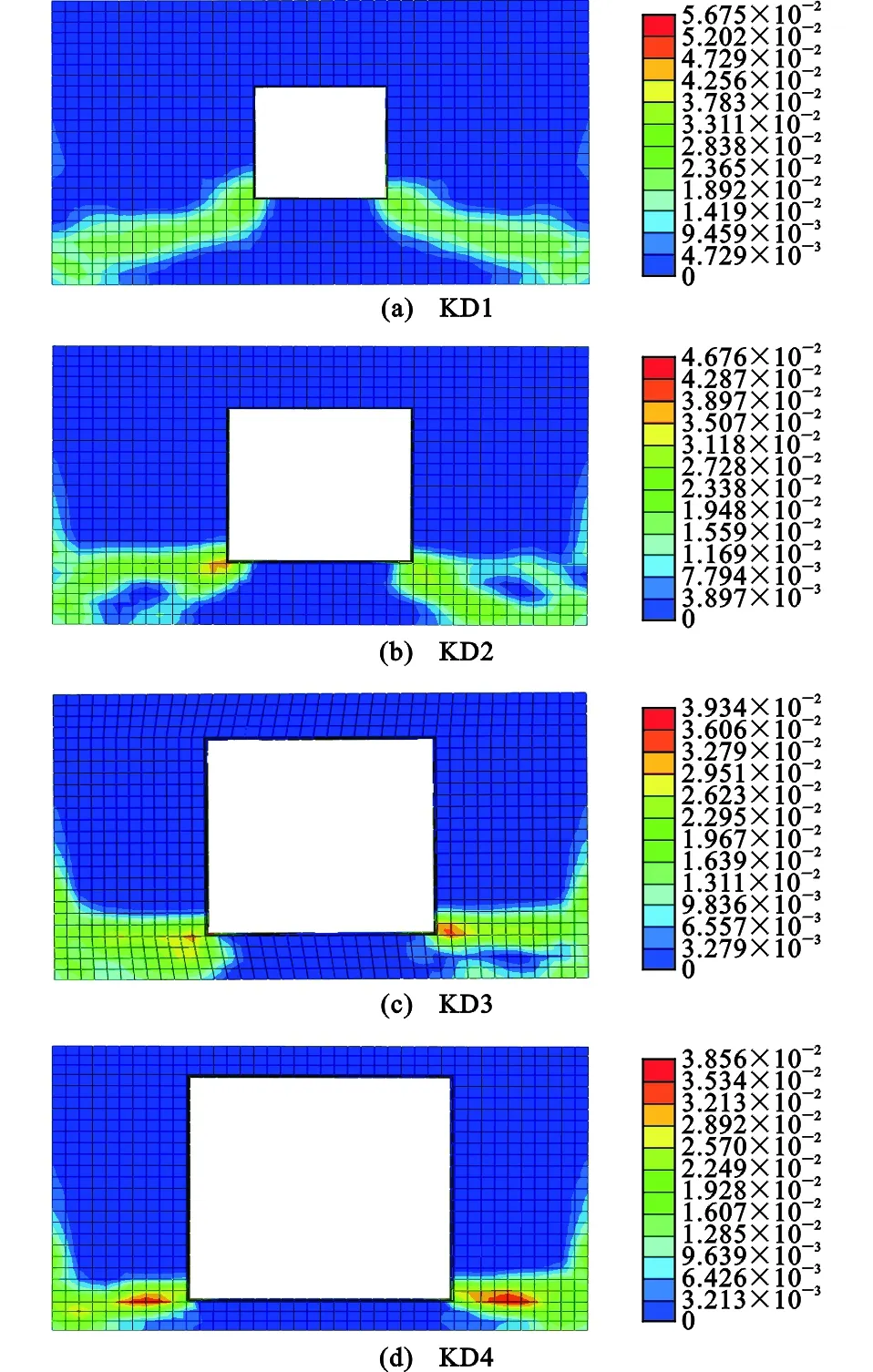
通过4组模型的等效塑性应变云图可以看出，所有模型墙体破坏最严重的部位都是墙体的下半区域，它们的破坏模式基本相同，都是在填充墙与框架柱的下半部分连接处出现破坏，裂缝向中部发展，最终与开洞的2个底角贯通。开洞底角处的破坏也十分严重。

等效塑性应变发展图可以一定程度上反映模型的破坏速度，将每个时刻模型中的最大等效塑性应变绘制成曲线，见图7。

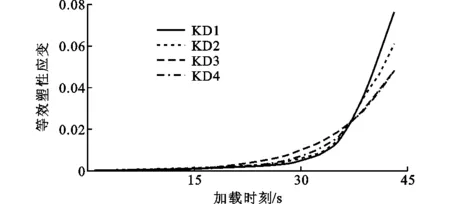
加载前期，所有模型的等效塑性应变增长都相对缓慢(图8)，其中KD1的增长速度最快，在同一个循环内的等效塑性应变不增长；KD2和KD4的增长速度基本相同，在同一个循环内的等效塑性应变几乎不增长；KD3的的增长速度最慢，在同一循环内的等效塑性应变有轻微增长。此时KD1的等效塑性应变累积最大。

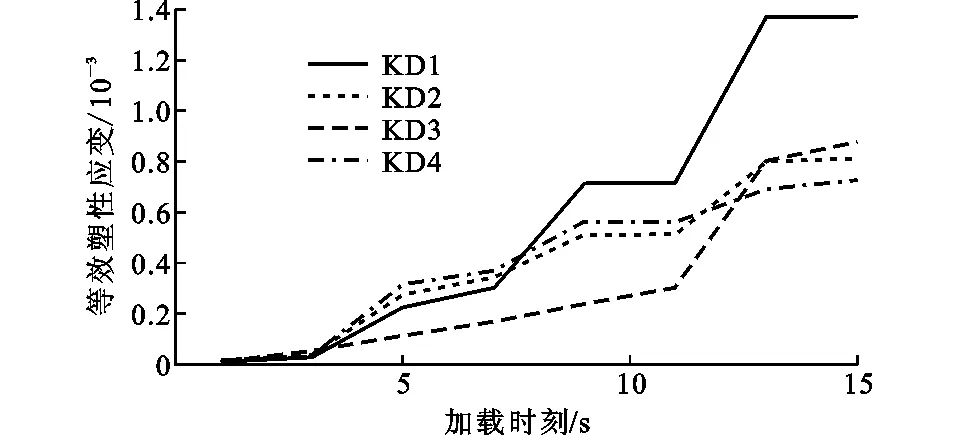
加载中期，所有模型的等效塑性应变增长有小幅度的提升(图9)，其中KD3的增长速度最快，KD4的增长速度次之，曲线斜率不断增加，等效塑性应变在同一个循环内有明显的增加；KD1和KD2的增长速度相对较慢，等效塑性应变在同一个循环内有小幅增加。此时的等效塑性应变累积量由大到小依次为KD3，KD4，KD2，KD1。

加载后期，所有模型等效塑性应变增长均有大幅度的提升(图10)，曲线的斜率都在不断增加，其中KD1的增长速度最快，KD2次之，KD3和KD4的增长速度相当。在这个阶段，每个模型在同一循环中的等效塑性应变均有大量的增加。此时等效塑性应变累积量KD1最大。

本节通过对框架结构外纵墙不同开洞率的数值模拟，可以看到以下现象：在平面位移作用下，框架填充墙的破坏都集中在填充墙的下半部分；墙体的裂缝开始于墙体的底角，容易与在开洞底角产生的裂缝贯通；墙体开洞率对墙体的破坏模式有很大影响，墙体的开洞率越大，开洞下方的墙体破坏面积就越大，开洞侧边与墙体之间的结构破坏面积就越小。墙体的开洞率与结构的破坏过程有关，墙体的开洞率越小，产生的破坏就越突然，在加载后期出现突然猛增，类似于结构的脆性破坏，在实际结构中更容易产生严重的后果。

3 开洞位置对RC框架填充墙平面外受力性能的影响

在本节中将研究开洞位置对纵墙平面外受力性能的影响[16]。选取开洞率为10%的200 mm厚填充墙为基础，框架尺寸不变，具体如表3所示。

表3 不同开洞位置的框架填充墙模型Tab.3 Frame Filled Wall Models with Different Opening Positions

3.1 不同开洞位置的填充墙应力云图分析

对不同开洞位置的框架填充墙平面外位移荷载作用下的应力云图进行详细分析[17-18]。随着位移荷载增加，填充墙的应力发展见图11。

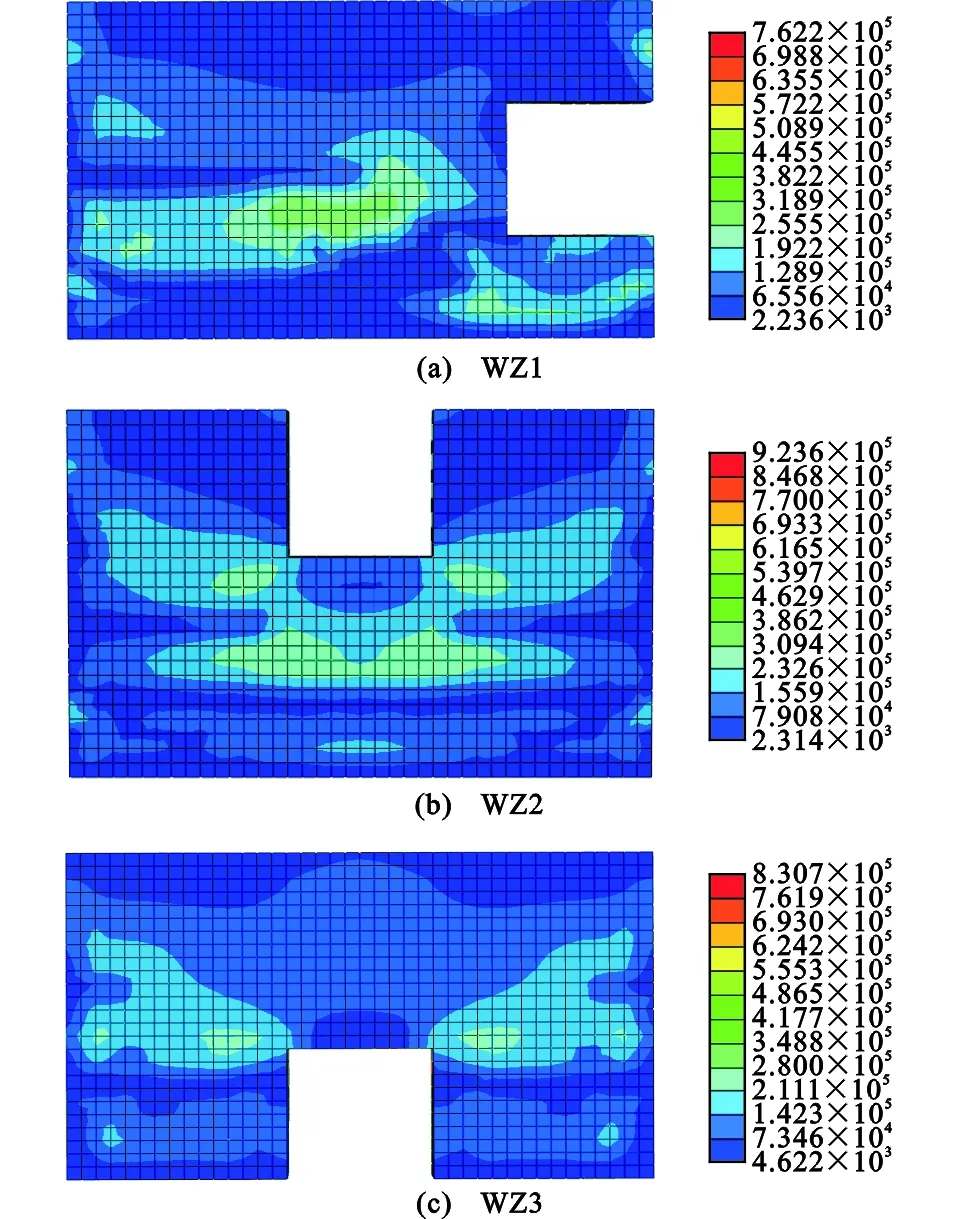
当平面外层间位移角达到1/1 000时，在此循环中，填充墙的底角边界处都出现了应力集中，并且已经达到材料的抗拉极限应力，与之前的模型类似。当平面外层间位移角达到1/700时，每个模型边界处的应力集中区域开始沿边界向上移动。当平面外层间位移角达到1/500时，在先前2个循环中边界处应力集中的位置出现了明显的应力下降。当平面外层间位移角达到1/300时，在此循环中每个模型的应力下降段都出现了不同程度的发展。当平面外层间位移角达到1/200时，所有模型都出现了应力下降贯通区域。当平面外层间位移角达到1/150时，所有模型都出现了大面积的应力下降区域，其中WZ1的左侧边界处应力下降区域还在不断向上发展，几乎贯通了整个边界，在填充墙中部也出现了一个横向发展的应力下降区域，此时应力集中在填充墙的中部；WZ3边界处的应力下降区域有小部分的增长。

通过以上的云图分析，对框架填充墙的纵墙平面外受力特征点相对应的层间位移角进行了总结，见表4。

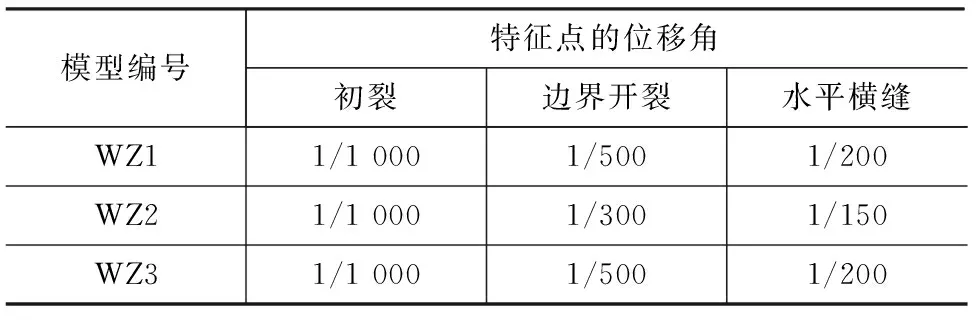
表4 墙体平面外破坏特征点的位移角2Tab.4 Displacement Angle 2 of Failure Feature Points Outside Wall Plane

通过以上的数据整理可以大致推测，开洞的位置对于墙体的初裂没有太大影响；开洞位置越靠近底部，边界开裂时位移角越小，其出现水平横缝的位移角也越小。

3.2 不同开洞位置的填充墙等效塑性应变云图分析

本节选取层间位移角为1/700，1/200，1/100，1/65，1/35，1/25时的等效塑性应变云图进行分析[19-20]，见图12。通过对3组模型的等效塑性应变云图分析可以看出，所有模型的破坏都集中在填充墙的下半部分，主要是填充墙两侧底角和框架处的界面出现破坏以及填充墙开洞周围破坏。

等效塑性应变发展图可以一定程度上反映模型的破坏速度，将每个时刻模型中的最大等效塑性应变绘制成曲线，见图13。

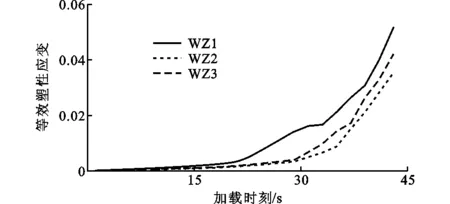
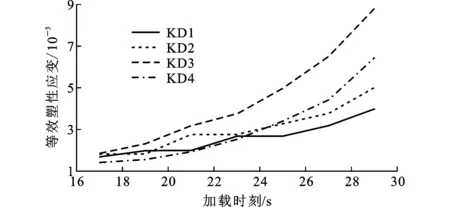
加载前期，所有模型的等效塑性应变增长速度都相对平缓(图14)，其中WZ1的增长速度最快，在同一个位移循环中等效塑性应变有小幅增加；WZ3增长速度次之，在同一个循环中等效塑性应变有小幅增长；WZ2的增长速度最慢，在同一个循环中等效塑性应变几乎不增加。此时等效塑性应变累积量由大到小依次为WZ1，WZ3，WZ2。

加载中期，等效塑性应变的增长速度出现了明显的差异(图15)，其中WZ1的增长速度最快，斜率突然变大，在同一循环中出现了等效塑性应变大幅增长；WZ2和WZ3的增长相对平缓很多，在同一循环中等效塑性应变有小幅增长。这个阶段WZ1的等效塑性应变累积量远大于其他2个模型，WZ3略大于WZ2。

加载后期，所有模型的等效塑性应变都出现了大幅的上涨(图16)，曲线的斜率基本相近，等效塑性应变累积量从大到小依次为WZ1，WZ3，WZ2，每个模型在同一循环中的等效塑性应变都出现了大幅增长。

通过对框架结构外纵墙不同开洞位置的数值模拟可以看出，开洞的位置对结构的破坏形式影响很大。在平面外位移作用下，开洞的位置与整体结构不是几何对称时更容易造成结构应力和应变的集中；开洞接近墙底部的结构比开洞接近墙体顶部的模型破坏更加严重；开洞位于顶部的结构破坏模式与满布填充墙类似；开洞位于中间时在开洞的底角出现了明显的破坏，开洞位于下方时开洞的4个角均出现了明显的破坏。开洞的位置与结构的破坏过程有关，开洞位置不规则时填充墙的破坏层间位移角更小，最终产生的等效塑性应变最大。

4 开洞形状对RC填充墙平面外受力性能的影响

取开洞率为20%的200 mm厚外纵墙为基础，框架尺寸不变，建立开洞高宽比为1/4，1/2，2/1，3/1四种不同形状的长方形开洞进行模拟分析(表5)。

4.1 不同开洞形状的填充墙应力云图分析

对不同开洞率的框架填充墙平面外位移荷载作

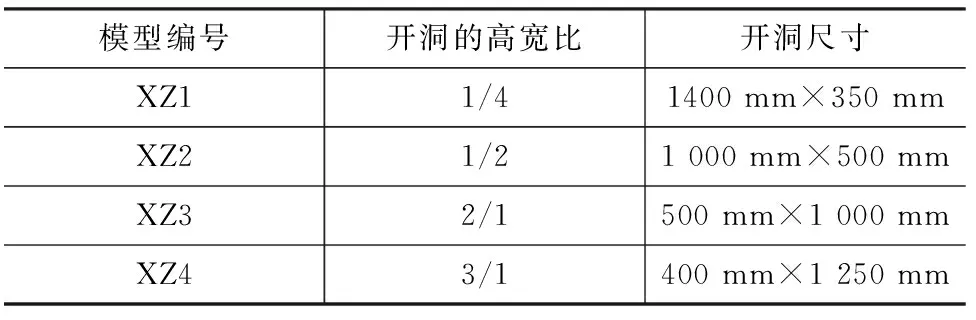
表5 不同开洞形状的框架填充墙模型Tab.5 Frame Filled Wall Models with Different Opening Shapes

用下的应力云图进行详细分析。随着位移荷载增加，填充墙的应力发展见图17。

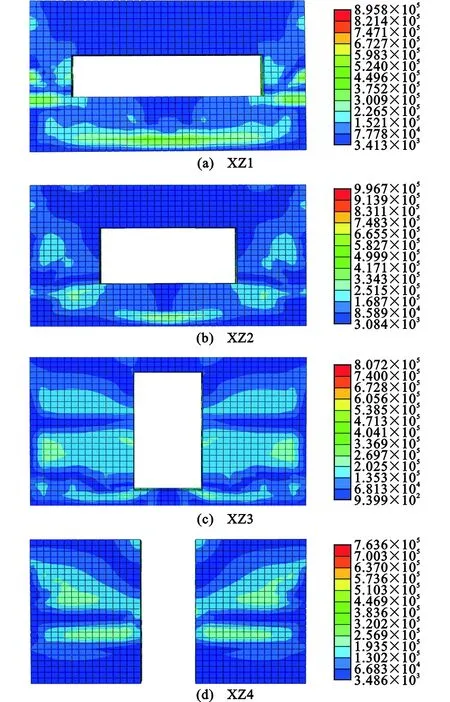
当平面外层间位移角达到1/1 000时，4个模型都在填充墙两侧底角边界处出现了明显的应力集中，并且应力大小均已经达到了材料的抗拉极限。结构模型在开洞的下方均出现了不同程度的应力分布，其中XZ1的分布比例最大，XZ2次之，XZ3最小；当平面外层间位移角达到1/700时，4个模型的应力分布区域都出现了不同程度的减小，减小程度从大到小依次为XZ1，XZ2，XZ3，XZ4。当平面外层间位移角达到1/500时，在这个循环中，之前加载步中应力集中的位置此时都出现了明显的应力下降区域。当平面外层间位移角达到1/300时，4个模型都出现了明显的应力下降区域。当平面外层间位移角达到1/200时，XZ1和XZ2的应力大小分布及下降区域的分布都没有明显变化，XZ3和XZ4在填充墙中部有1条横向的应力下降区域正在发展。当平面外层间位移角达到1/150时，XZ1和XZ2边界处出现了大部分的应力下降；XZ3和XZ4填充墙中部发展的应力下降区域已经贯通，边界处也出现了大跨度的应力下降区域，此时XZ4的结构底部出现了大面积的应力下降区域。

通过以上的云图分析，对框架填充墙纵墙平面外受力特征点对应的层间位移角进行总结，如表6所示。

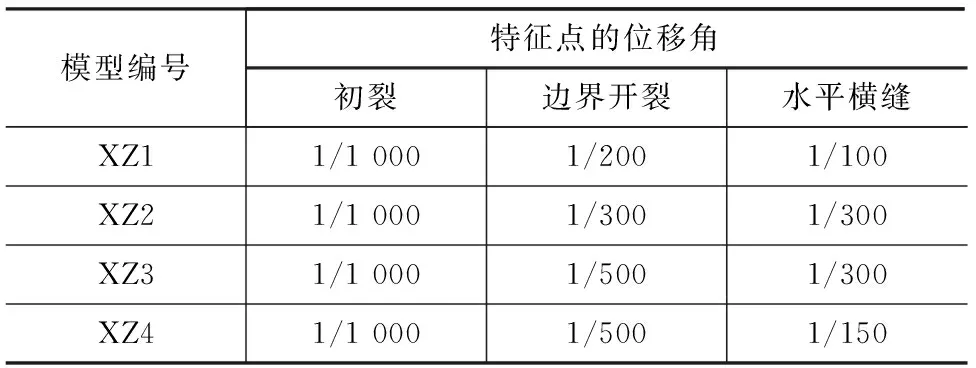
表6 墙体平面外破坏特征点的位移角3Tab.6 Displacement Angle 3 of Failure Feature Points Outside Wall Plane

通过对不同开洞高宽比的模型分析，可以看到XZ1和XZ2在加载的最后阶段应力分布没有特别明显的变化，XZ3和XZ4在加载的最后阶段应力下降十分迅速。根据以上可以初步推测，开洞形状对于结构的初裂没有太大影响，模型开洞的高宽比越大，模型边界产生开裂的层间位移角越小。开洞的高宽比越小，边界开裂和水平横缝出现的层间位移角越大，结构的平面外受力性能就越好。

4.2 不同开洞形状的填充墙等效塑性应变云图分析

选取层间位移角为1/700，1/500，1/200，1/65，1/35，1/25时的4组不同开洞形状模型的等效塑性应变云图进行详细分析(图18)。可以看出，所有模型的破坏均是由填充墙底角发生应变集中，随着荷载循环的增加开洞底角也出现应变集中，随之裂缝贯通，填充墙破坏。

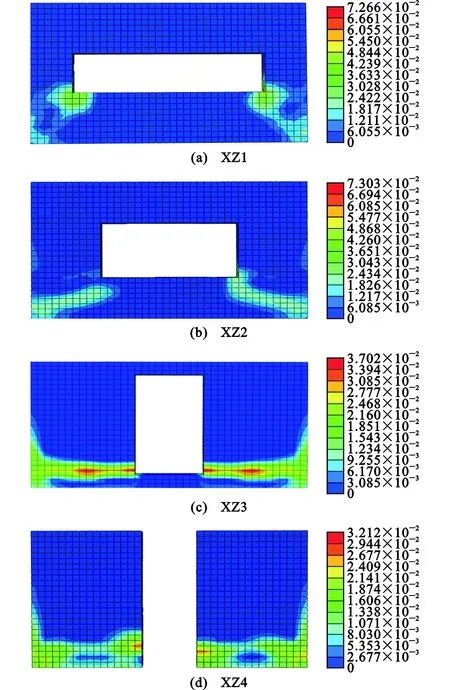
等效塑性应变发展图可以一定程度上反映模型的破坏速度，将每个时刻模型中的最大等效塑性应变绘制成曲线，见图19。

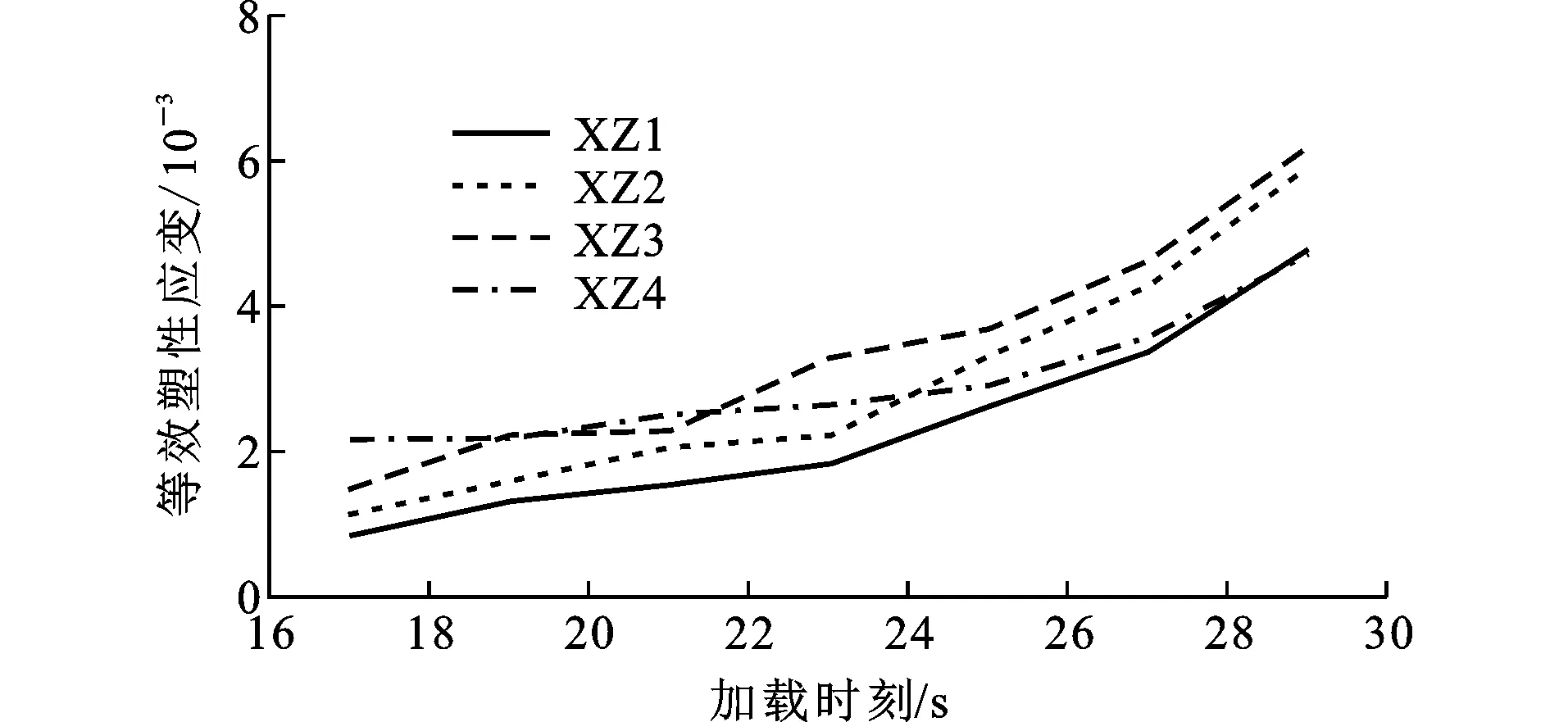
加载前期，所有模型的等效塑性应变都在缓慢增长(图20)，其中XZ1和XZ2的增长速度最缓慢，曲线的斜率最小，在同一个循环内应变相对增长；XZ3的增长速度较快，在同一个荷载循环内应变小幅增长；XZ4的应变速度增长最快，在同一个循环内应变的增长相对不明显。

加载中期，XZ1和XZ2的应变增长速度明显加快，曲线斜率迅速增长，XZ4的应变增长速度相对变小，曲线斜率增长缓慢；其中XZ1，XZ2和XZ3曲线的斜率都接近，此时应变累积量XZ3最大，XZ4应变累积最小。在同一个循环内等效塑性应变除XZ4增长不明显外，其余均有明显的增长(图21)。

加载后期，XZ1和XZ2的应变迅速增长，结构的等效塑性应变由大到小依次为XZ1，XZ2，XZ3，XZ4，等效塑性应变在同一个循环内均有明显的增长，其中XZ1的增长量最大，XZ4的增长量最小。加载最后阶段的等效塑性应变累积量XZ1，XZ2约为XZ3，XZ4的2倍(图22)。

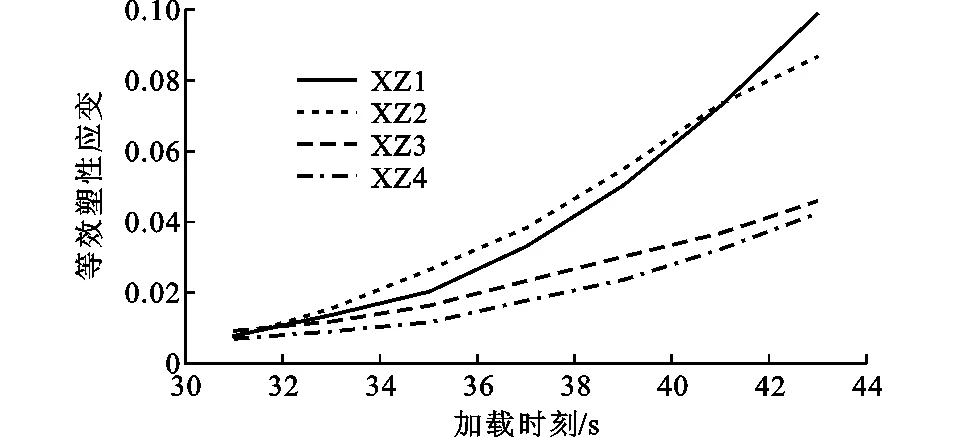
本节通过对框架结构纵墙不同开洞形状的数值模拟，可以看到以下几种现象：开洞高宽比越小，加载前期的应变越小，加载后期开洞应变的发展越快，应变累积量越大。开洞形状对纵墙的破坏形式有很大的影响，开洞高宽比小于1的结构破坏形式都是由填充墙两侧底角至开洞底角产生破坏，最终是斜向的破坏。开洞高宽比大于1的结构破坏形式都是填充墙两侧底角处的边界破坏，然后横向发展，最终破坏是整个填充墙底部都产生破坏。

5 结 语

(1)在平面外单调加载作用下，纵墙的开洞率、开洞位置、开洞形状对结构的初始破坏没有太大影响，墙体的初始破坏都出现在填充墙两侧底角处。在RC框架填充墙开设相同开洞条件下，相比于框架填充墙单调加载，反复加载作用下框架填充墙的承载力、刚度和延性比都降低了。

(2)当纵墙的开洞率不同，墙体开洞率较大时，最终结构破坏形态是底部横向破坏，反之是边界底角到开洞底角的斜向破坏。开洞率越大，边界出现裂缝层间位移角越大，出现水平通缝的层间位移角越小，加载最后的等效塑性应变累积量越小。因此，建议采用开洞率20%较为合理。

(3)当纵墙的开洞位置不同，开洞与结构几何对称时，结构的受力性能更好。开洞越接近结构底部，模型边界出现裂缝的层间位移角越小，结构出现水平横缝的层间位移角也越小，结构发生大面积破坏的层间位移角越小，最终结构的应变累积越大。因此，开洞大小一定时，建议开洞边缘靠近底梁，横向居中。

(4)当纵墙的开洞形状不同时，开洞高宽比越小，模型边界开裂的层间位移角越大，水平横缝出现的层间位移角越大，模型最终的应变累积越大。开洞高宽比小于1时，模型的破坏形式都是由填充墙两侧底角至开洞底角产生破坏，最终是斜向破坏；开洞高宽比大于1时，模型的最终破坏形式为墙体底角至开洞边缘的横向破坏。在开洞面积一定时，开洞的高宽比越小，结构的平面外受力性能就越好。因此，建议采用开洞高宽比较小值。