整体桥预应力桩-土相互作用试验
2021-01-29黄福云何凌峰单玉麟王静杰
黄福云,何凌峰,单玉麟,王静杰,张 峰
(1. 福州大学土木工程学院,福建福州 350108; 2. 福州大学福建省土木工程多灾害防治重点实验室,福建福州 350108)
0 引 言
整体式桥台无缝桥(简称整体桥)取消了桥台处的伸缩缝和伸缩装置,从而避免了设置伸缩缝导致的养护维修问题,提高了桥梁结构的安全性和耐久性,在欧洲和北美得到了大量推广应用[1-2]。由于整体桥上部结构与桥台桩基固接,上部结构在昼夜及季节性温度循环作用下产生的纵桥向变形需通过桥台的往复运动和桩基的水平变形来吸纳,产生复杂的结构-土相互作用[3-5]。因此,为保证整体桥桩基具有较好的变形能力,常采用柔性桩[6]。不过,对于这类桥桩基的选用、设计以及相关构造细节目前并不统一,也存在着较大的差异。
Dunker等[7]对美国整体式桥台桩基类型进行了调查,结果表明整体式桥台桩基类型主要有H型钢桩、混凝土(RC)桩、预应力混凝土(PC)桩、预应高强混凝土(PHC)管桩、钢管混凝土(CFST)桩、木桩等,其中70%的桩基采用了H型钢桩[8]。不过,虽然H型钢桩在水平变形和强度方面有明显的优势,但在土质较差的环境中容易受到腐蚀且经济性较差,在打桩过程中也经常发生屈曲现象[9-10]。因此,混凝土桩在国内外无缝桥中具有一定的应用,且由于经济条件和工程习惯,中国已建的无缝桥大都采用混凝土桩。Gama等[11]对混凝土桩支承的整体桥进行了有限元参数分析,分析结果表明只要设计合理,完全可以克服混凝土桩开裂的问题,在水平位移荷载作用下往往需要通过复杂的构造措施才能保证混凝土不发生开裂[12]。为解决混凝土桩的开裂问题,采用施加预应力的方法改善其水平变形能力和受力特性是一种可行的方法。
一些研究表明,PC桩桩基并不适用于无缝桥[13-14]。不过,国外已有一些整体桥应用了PC桩的工程实例。为明确PC桩的适用性,Burdette等[15]开展了4根预应力桩的试验,结果表明:当桩头水平位移减小到0时,桩中的预应力有效地闭合了裂缝;循环荷载下,桩的刚度只有很小的降低,证明了预应力桩具有良好的工作性能,可用于整体桥桥台桩基。Joen等[16]进行了螺旋箍筋对PC桩延性性能的影响研究,结果表明,预应力混凝土桩在采用合理的螺旋箍筋设计下具有良好的延性。Kamel等[17]对预应力桩的刚度进行了研究,结果表明预应力对桩的刚度有较大影响。Harries等[18]开展了预应力桩与桩帽连接节点的承载力试验研究,结果表明当桩端嵌入长度足够长时,可以有效地传递弯矩且不会破坏连接节点。Kong等[19]对一座采用预应力方桩的整体桥进行了实桥检测,结果表明预应力桩的最大微应变未超过混凝土的开裂应变,其工作性能良好。
总体来说,整体桥预应力桩-土相互作用与受力性能的研究还不深入,其是否适用于该类型桥梁还不明确,中国在该方面的研究工作开展较少。为此,本文进行了3根预应力混凝土PC桩在砂土中的低周往复拟静力试验,从桩-土相互作用的破坏模式、桩身应变、桩身位移、桩身弯矩以及PC桩抗震性能等角度,探究了预应力对其水平受荷性能的影响。同时,通过与埋深不同且未施加预应力的混凝土桩对比,进一步说明预应力对柔性桩变形能力的影响,为整体桥在中国的推广应用提供理论依据和技术支撑。
1 模型试验
1.1 模型桩设计
本试验设计制作了3根模型桩,编号分别为PC-1,PC-2和PC-3。桩径均为155 mm,相似比为0.31。3根模型桩均采用C40混凝土,具体参数见表1。根据文献[20]所述,《公路桥涵地基与基础设计规范》(JTG D63—2007)中对于柔性桩的判断方法偏不安全,而Broms的判别方法更为合理。根据Broms法计算得到横向刚度系数为0.77,则桩长大于3.08 m可判断为柔性长桩。考虑场地及土箱尺寸等试验条件,本试验桩长取为3.5 m。
定义预应力度β为预应力与混凝土抗压强度的比值。PC-1,PC-2和PC-3的预应力度分别取为0.0%,12.5%和25.0%。预应力筋采用公称直径为15.2 mm的7股标准预应力钢绞线,并通过油压千斤顶对预应力筋进行张拉。在张拉过程中通过力传感器严格控制PC桩的有效预应力值,根据设计的预应力度,最终PC-2和PC-3模型桩的张拉控制力分别为45,90 kN。具体参数见表2。

表1 模型桩混凝土参数Tab.1 Concrete Parameters of Model Pile
1.2 土箱和试验土
试验土箱需满足土的边界条件要求,通常取5倍桩径的距离即可满足要求[21]。综合考虑试验成本,土箱的尺寸选取3 m×2 m×4 m,如图1所示。

本试验砂土采用闽江河砂,具体砂土参数见表3,砂土颗粒级配曲线见图2。经过标准贯入试验测得模型砂土平均贯击数为11,根据《岩土工程勘察规范》(GB 50021—2001)可知,本试验砂土属于稍密砂,相对密实度为53%。在砂土装箱过程中,每装25 cm厚就对砂土进行压实,以此保证其均匀性。
1.3 测点布置
本次试验选用了位移计、混凝土应变片、钢筋应变片以及土压力盒。为了测得桩身拉、压应变变化历程,分别在混凝土表面和纵筋处布置了应变片,每根桩各布置44个应变片,其中混凝土和钢筋各22个应变片。应变片由桩顶至桩底编号,其中,混凝土应变片受力方向两侧的编号分别为C1~C11和C12~C22;钢筋应变片受力方向两侧的编号分别为S1~S11和S12~S22,等间距布置,间距为350 mm。考虑到一般在3倍~5倍桩径的埋深处桩身弯矩达到最大[21],因此对该区域进行了加密。同时,为了测得水平荷载作用下,桩周土抗力沿桩身的分布情况及变化历程,分别在桩侧混凝土表面布置了16个土压力计,受力方向两侧各8个,编号分别为T1~T8和T9~T16,等间距布置,间距也为350 mm。本次试验采用了文献[21]中提出的测量桩身位移的方法,文献[20],[22]中试验也采用该方法测量桩身位移,结果精准可靠。共安装12个位移计,由桩顶至桩底编号依次为D1~D12。除最底下的D12间距为600 mm外,其余位移计间距均为200 mm。各测点布置如图3所示。

表3 砂土的物理力学参数Tab.3 Physical and Mechanical Parameters of Sand


1.4 试验装置与加载制度
试验采用MTS电液伺服加载系统在桩顶施加往复水平位移。具体加载方案为:加载初期按2,5,8,10 mm进行位移加载;10~30 mm范围内,每级位移荷载增量为5 mm;30 mm以后每级位移增量为10 mm,加载历程如图4所示。
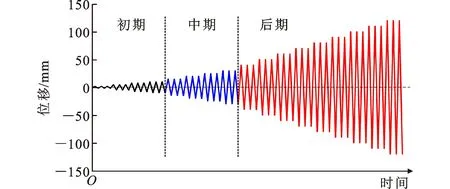
根据《建筑抗震试验规程》(JGJ/T 101—2015),当模型桩水平承载力下降到极限承载力的85%时,认为模型桩破坏并停止加载。试验时的加载速度为1.0 mm·s-1,每级荷载循环3次。
2 模型试验结果
2.1 破坏形态
试验加载结束后,首先将砂土从预留的出砂口卸出,然后再将桩取出,观察其破坏情况。图5给出了3根模型桩的破坏照片,并将破坏情况列于表4。

由图5和表4可知,PC-1,PC-2均有3道比较明显的裂缝,PC-1的破坏位置主要集中在3.2D,4.0D,5.0D处,其中主要裂缝在4.0D处,裂缝贯通整个截面,纵筋裸露在外但没有发生明显的屈服,3.2D,5.0D处混凝土仅发生轻微的开裂,如图5(a)所示。PC-2的破坏程度和PC-1相似,破坏位置集中在3.6D,4.4D,5.3D处,其中4.4D处的裂缝最为明显,混凝土裂缝贯通截面,但两侧纵筋同样没有发生明显屈服,3.6D,5.3D处混凝土表面仅有轻微的开裂,如图5(b)所示。PC-3只有1道明显的主要裂缝,破坏集中在4.6D处,塑性铰区两侧纵筋明显屈服且混凝土被严重压碎,如图5(c)所示,其他位置裂缝较细微。
3根模型桩主要裂缝出现位置及钢筋屈服情况存在差异,表明预应力对混凝土桩的破坏模式有较大的影响。文献[20]对3根桩长不同且未施加预应力的混凝土桩进行了拟静力试验,桩编号分别为RC-1,RC-2,RC-3,均采用C40混凝土,配筋率及桩径均与本试验中模型桩一致。为了进一步说明预应力对桩身破坏的影响,将本试验结果与文献[20]进行对比。模型桩主要破坏位置埋深及影响因素见表5。

表4 模型桩破坏情况Tab.4 Damage of Model Pile

表5 主要破坏位置及影响因素Tab.5 Main Damage Positions and Influencing Factors
对比可知,在未施加预应力的情况下,RC-1和PC-1主要破坏位置埋深相近,但小于RC-2和RC-3,表明增大埋深在一定程度上可增大桩-土相互作用区域,改善桩身变形能力。施加预应力后,虽然PC-2的埋置深度小于RC-3,但其主要破坏位置埋深大于RC-3,表明在配筋率一致的情况,相对于增大桩的埋深,增大预应力度能够更有效地提高混凝土柔性桩的变形能力。对比PC-2和PC-3的破坏情况可知,随着预应力的进一步提高,桩身破坏模式由1道主要裂缝伴随多条微裂缝向仅有1道主要裂缝转变,同时钢筋发生屈服。这表明预应力增加使得桩基所受土压力也进一步提高,桩-土相互作用更加显著,桩基变形能力得到更加充分的发挥。
2.2 桩身应变
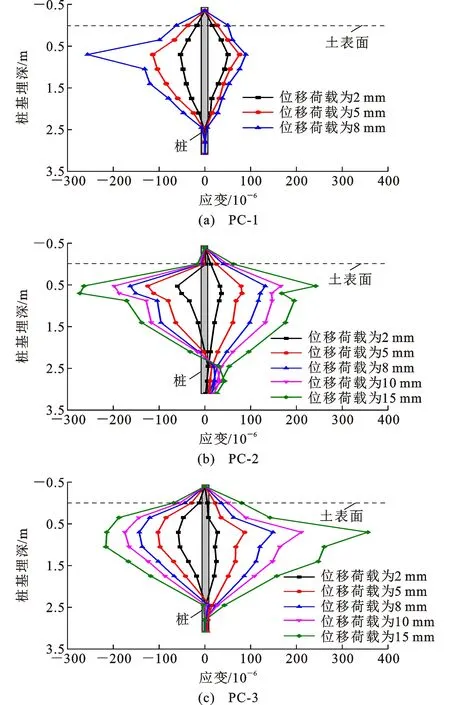
本试验通过模型桩两侧应变片的应变分布规律来大致判断模型桩的开裂位移和开裂荷载。由于测点位置与桩身开裂位置接近,当混凝土达到开裂荷载时,混凝土应变片损坏。因此,桩身应变分布只给出了初期加载结果,如图6所示。由图6可知,当加载位移较小时,各试件的拉、压应变分布较为对称。当加载位移达到8 mm时,PC-1拉、压应变开始出现不对称,压应变迅速增加而拉应变增加较小,表明此时混凝土桩已经开裂。因此,可认为PC-1的开裂位移为8 mm,这与文献[20]中RC-2的开裂位移一致;对于PC-2和PC-3,当加载位移达到15 mm时,拉、压应变分布仍较对称,说明混凝土桩仍处于弹性受力状态。因此,可认为其开裂位移大于15 mm,同时也大于文献[20]中RC-3的开裂位移(10 mm)。上述现象表明,相较于增大桩基埋深,施加预应力可更为有效地增大混凝土桩基的弹性工作范围,提高桩基的整体性和抗开裂能力。
2.3 桩身弯矩
当模型桩处于弹性范围内时,可以基于平截面假定,近似地通过两侧的应变值换算得到沿桩深方向的弯矩分布规律,如公式(1)所示
(1)
式中:M为桩身弯矩;εt为拉应变;εc为压应变;E为桩身混凝土弹性模量;I为截面惯性矩。
图7给出了各试件的桩身弯矩分布规律。由图7可知,不同位移荷载作用下,3根模型桩的桩身弯矩分布趋势相同,呈现为中间大两端小的抛物线型,最大弯矩值基本位于4.0D~5.0D处,与第2.1节模型桩的破坏位置相接近。3根模型桩的最大弯矩值分别为1.65,2.03,2.24 kN·m,PC-2和PC-3分别较PC-1提高了23%和36%。说明预应力增加,弯矩承载力也明显增加,在进行相关设计和计算时应考虑预应力对水平受荷桩受力性能的影响。
为评估桩-土相互作用效果,文献[22]定义了桩基弯矩承载比例系数γp,γp来反映桩基在桩-土体系中的承载力大小,其计算公式如下
γp=MT/ML
(2)
式中:MT为考虑桩-土相互作用的试验弯矩;ML为忽略土体作用的计算弯矩。
ML可由式(3)计算
ML=Fl
(3)
式中:F为MTS对桩基施加的外力;l为外力臂臂长,即外力作用点至最大弯矩处的距离,取0.7 m。
MT和ML满足式(4),其中MS为土抗力作用产生的弯矩。
ML=MT+MS
(4)
表6给出了PC-2和PC-3加载至5 mm和10 mm位移荷载时,在0.7 m埋深处的实测弯矩、桩顶外力矩及其比值。由于PC-1开裂较早,混凝土应变片发生损坏,因此仅给出加载至5 mm和8 mm时的计算结果。同时将文献[20]中3根模型桩在加载至5 mm和8 mm时的桩基承载比列于表6。由于文献[20]中并未给出具体弯矩值,因此表6也未列出。
由表6可知,位移荷载为5 mm时,6根模型桩的承载比均超过了50%,可见此时桩-土体系荷载主要由桩身提供。随着位移荷载增加,3根模型桩的桩基承载比均呈下降趋势。未施加预应力的4根模型桩(RC-1,RC-2,RC-3和PC-1)及施加部分预应力的模型桩(PC-2)桩基承载比始终大于50%。预应力较大的PC-3在加载至8 mm时桩基承载比就降至50%以下。说明随着位移的增加,桩侧土体承担了更多荷载,并随着预应力的增加进一步增大。
对比各加载位移下的桩基承载比可以发现,未施加预应力的4根模型桩(RC-1,RC-2,RC-3和PC-1)的桩基承载比随着桩基埋深的增大而减小,符合文献[20]中的规律。同时,还可发现PC-2的桩基承载比小于RC-3,说明相较于增大桩基埋深,施加预应力能够更加有效地增加土体参与受力,改善桩身变形能力。对比PC-2和PC-3可知,预应力越高,桩基承载比越低,桩基变形性能越好。
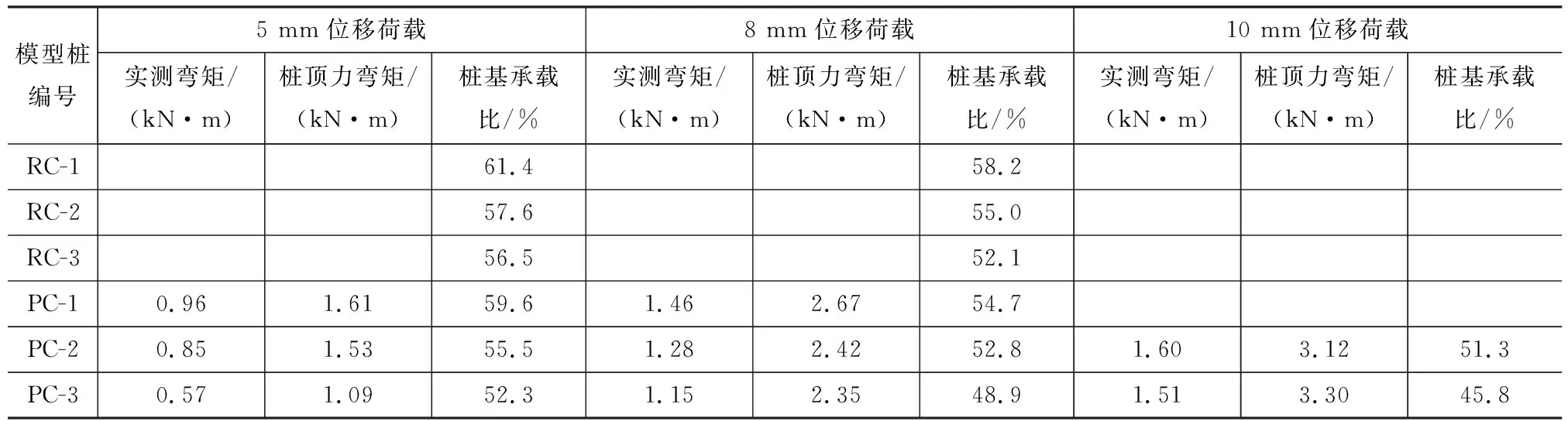
表6 模型桩弹性阶段水平力承载比Tab.6 Horizontal Load-bearing Ratio at Elastic Stage of Model Pile
2.4 桩身位移
加载位移较小(2~15 mm)时,各模型桩在相同的位移荷载作用下桩身位移曲线总体趋势基本相同,仅在较深的位置桩身位移有所差异。限于篇幅,图8仅给出了正向100 mm位移荷载作用下各模型桩沿桩深方向的桩身位移曲线对比。

从图8可知,3根模型桩的位移反弯点位置分别在埋深4.2D,5.3D,5.4D处。该现象表明,预应力度的提高使得临界位移点沿桩身向下发展,增大了桩-土相互作用区域。当达到临界位移之后,PC-1,PC-2和PC-3的最大反向位移分别为-2.0,-2.4,-2.6 mm,说明预应力的提高也增大了埋深较大处的桩-土相互作用。由第2.3节可知,加载后期,桩身承载力达到极限之后不再增加,水平承载力主要由桩周土水平抗力提供。因此,桩-土相互作用区域的增加可进一步发挥桩周土的束缚作用,有助于提高桩-土体系的水平承载能力。
2.5 骨架曲线
取各级位移荷载所对应的峰值荷载,绘制得到各模型桩-土体系的骨架曲线,如图9所示。

由图9可知:PC-1,PC-2和PC-3骨架曲线变化发展规律基本一致。位移荷载较小时,骨架曲线基本呈线性;随着位移荷载增加,桩-土体系发生塑性变形,桩-土体系开始分离,模型桩产生裂缝并屈服,骨架曲线开始出现非线性,斜率逐渐减小;达到极限承载力之后,桩-土体系进入破坏阶段,骨架曲线开始下降,模型桩损坏严重,承载力下降明显。
2.5.1 临界荷载
通过骨架曲线可进一步得到加载桩顶荷载-位移梯度曲线[23]。位移梯度通过ΔY0/ΔP(ΔY0,ΔP分别为骨架曲线相邻点的位移差值和荷载差值)计算得到,即骨架曲线相邻两点连线斜率的倒数。由于骨架曲线正向、反向较为对称,限于篇幅,图10仅给出正向计算结果,正向、反向具体计算结果见表7。通过荷载-位移梯度曲线可看出,桩身受力可分为3个阶段,分别为弹性变形阶段、弹塑性变形阶段和破坏阶段。ΔY0/ΔP曲线上第一拐点对应弹性阶段的终点,其对应的水平荷载值和位移为临界荷载Pcr和临界位移Ycr。

从图10和表7可知,PC-1,PC-2,PC-3的临界荷载和临界位移分别为4.39 kN和9.02 mm,6.02 kN和17.53 mm,7.86 kN和22.54 mm。这表明预应力度的增加可显著提升桩土体系的临界荷载和
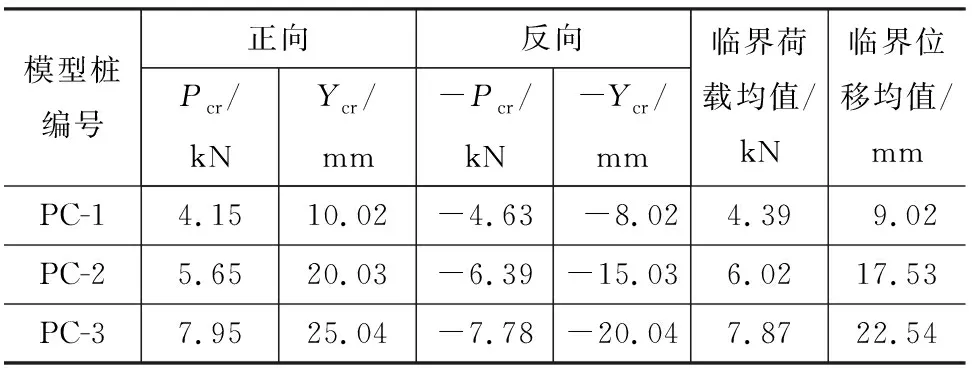
表7 模型桩临界荷载Tab.7 Critical Load of Model Pile
临界位移,即可提高其弹性工作范围。
2.5.2 屈服荷载和峰值荷载
通过能量等效法[24]可得到骨架曲线的屈服荷载和峰值荷载特征值,由于骨架曲线正向、反向较为对称,限于篇幅,图11仅给出正向计算结果,屈服荷载Py和屈服位移Yy计算结果见表8。
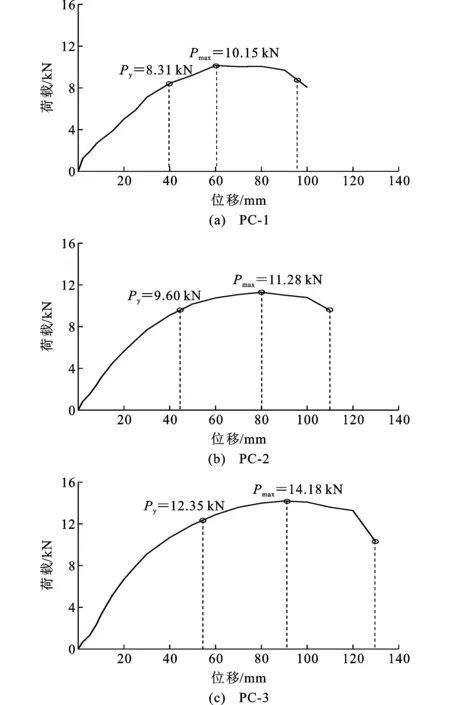
由图11和表8可知,随着预应力的增加,模型桩的屈服荷载、峰值荷载Pmax及其对应的位移均有所提高。PC-2和PC-3的屈服荷载分别比PC-1的提高了17.8%和42.3%,峰值荷载分别提高了11.1%和39.7%,屈服位移分别提高了12.0%和33.0%,峰值荷载对应的位移分别提高了33.3%和50%。
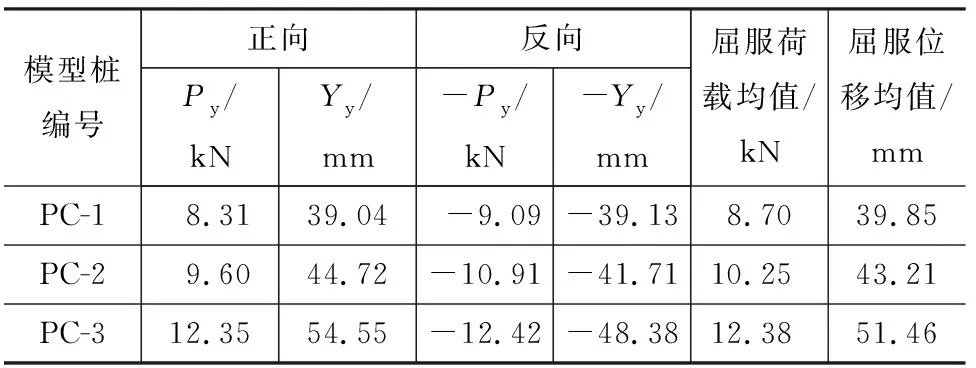
表8 模型桩屈服荷载Tab.8 Yield Load of Model Pile
2.6 等效刚度
根据《建筑抗震试验规程》,模型桩-土体系的等效刚度Ki可按下式计算
(5)
式中:±Pi,max分别为第i次循环正向、反向加载时对应的峰值点荷载;±Yi,max分别为第i次循环正向、反向加载时对应的峰值点位移。
从图12可知,模型桩-土体系的等效刚度变化趋势基本一致。相同位移荷载作用下,预应力大的模型桩其桩-土体系等效刚度要稍大一些。在0~20 mm加载位移时,PC-1率先开裂,等效刚度的退化速率要明显快于PC-2和PC-3。

文献[21]给出了PHC管桩等效刚度Kq的简化计算公式,即
Kq=f(y)Ke
(6)
式中:f(y)为与桩顶位移相关的系数;y为桩顶水平位移;Ke为模型桩弹性极限抗弯刚度。
Ke可根据下式计算得到
Ke=Pcr/Ycr
(7)
根据上式计算得到PC-2的弹性极限抗弯刚度为0.34 kN·mm-1。f(y)计算公式为
(8)
式中:ycr为弹性极限位移;ys为屈服极限位移。
PC-2的等效刚度如图13所示。

由图13可知,采用文献[22]的等效刚度退化公式计算得到的刚度退化曲线可以较好地反映预应力混凝土桩的刚度退化规律。不过,在20~60 mm加载位移内还是有较大的误差,但考虑到偏安全,可以采用公式(7)评估桩的刚度退化。
3 结 语
(1)随着预应力度的提高,桩身初始开裂位置沿桩身下移,桩身位移反弯点沿桩身下移,桩土作用区域增加。与不同埋深的未施加预应力的混凝土桩对比发现,在配筋率一致的情况下,相比于增大桩基埋深,增大预应力度能够更有效地提高混凝土柔性桩的变形能力。
(2)加载初期模型桩的拉、压应变较为对称。随着位移荷载的增加,PC-1的桩身拉、压应变分布率先出现不对称,而PC-2和PC-3在更大位移荷载时仍保持对称。通过与不同埋深的未施加预应力的混凝土桩对比发现,相较于增大桩基埋深,施加预应力可以更为显著地提高桩基的弹性工作范围及桩身的整体性和抗开裂能力。
(3)通过分析比较模型桩的桩身承载比可知,提高预应力度可改善桩身受力性能,更充分发挥桩周土的承载能力。
(4)随着预应力度的增加,模型桩-土体系的临界荷载、屈服荷载、峰值荷载均有所提高。屈服荷载分别较PC-1提高了17.8%和42.3%,说明预应力度可以增大混凝土桩的弹性工作范围,提高变形能力。
(5)预应力的提高减缓了模型桩等效刚度退化速率。采用PHC管桩等效刚度计算方法可较好地反映PC桩的刚度退化规律,且计算结果偏安全,可用于PC桩的等效刚度计算。
