Feistel结构的8比特轻量化S盒

董新锋，张文政，许春香

(1.电子科技大学 计算机科学与工程学院，四川 成都 611731；2.保密通信重点实验室，四川 成都 610041)

国内外现有的对称密码算法设计仍然沿用香农1949年提出的“混淆”、“扩散”思想[1]，通过对称密码算法的“混淆”和“扩散”部件使得明文、密文和密钥之间的关系异常复杂，以至于攻击者无法从密文得到明文的任何信息或者从明文密文对得到密钥的任何信息。“混淆”部件普遍采用非线性置换S盒(Substitution Box)。S盒首次出现在分组密码算法LUCIFER中，随着美国标准化技术研究机构(National Institute of Standard Technology，NIST)在1977年发布的数据加密算法标准(Data Encryption Standard，DES)的使用而广为流行[2]。S盒是绝大多数密码算法中唯一的非线性部件，如AES、CAMELLIA、ARIA、CLEFIA等[3-6]。S盒的密码性质极大影响整个算法的“混淆”效果，也几乎决定了整个密码算法的安全强度。

自2004年之后，针对物联网中RFID类资源受限设备的安全保密需求，密码算法设计时不仅要考虑密码算法及部件的安全性，同时要兼顾算法实现的硬件门数等资源指标。目前适用于RFID类资源受限设备的轻量级密码算法其硬件实现等效门一般不超过2000 GATE[7]，使用传统查表方式实现的S盒难以满足轻量级密码算法的硬件实现资源小等要求，特别是使用8比特S盒的情形。基于代数结构的S盒的轻量化实现、基于简单逻辑运算的S盒的轻量化设计等是当前国内外密码领域的研究热点问题之一，也取得了一些研究进展，如：对具有最优密码学性质的4比特S盒的16个等价类划分[8]，这类S盒已成功应用于设计PRINCE、MIDORI、SKINNY等轻量级分组密码算法[9-11]；NBC、SPRING等分组密码算法提出了16比特、32比特S盒的轻量化设计思路，但基于该设计思路的S盒需要迭代20轮或32轮，其实现方式具有较大的时延，32比特S盒目前仍难以完全刻画其差分均匀度和非线性度等密码性质[12-13]；在SKINNY-128分组密码算法中，设计者提出一种基于2个4比特S盒并置构成1个新的8比特S盒的设计思路[10]，但基于该设计思路的8比特S盒的差分均匀度和非线性度等密码性质较弱，会导致密码算法的整体迭代轮数较大，影响密码算法实现性能；美国标准化组织NIST先后启动了认证加密方面的CAESAR竞赛、轻量级AEAD和杂凑算法征集等活动，提交的密码算法方案中也对轻量化密码部件及其实现性能进行了一些研究[14-19]。

笔者提出一种新的8比特轻量化S盒设计方法，其单轮逻辑运算仅涉及4个单比特与运算和4个单比特异或运算，迭代4轮后差分均匀度为16(差分概率为2-4)、非线性度为96(线性概率为2-4)、分量函数代数次数可以达到6。与已有研究结果相比，设计的8比特轻量化S盒需要较少的硬件实现资源，同时达到了8比特轻量化S盒的已知最优差分均匀度和非线性度等密码性质，解决了之前8比特轻量化S盒差分均匀度和非线性度等密码性质较弱的问题。

1 S盒及其主要密码学性质

1.1 符号与定义

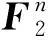
1.1.1S盒

n比特输入m比特输出的S盒(简称为n×m的S盒)定义如下：

1.1.2 布尔函数的代数正规型、项数和代数次数

每一个n元布尔函数f都可以唯一地表示为F2上关于n个变元x1，x2，…，xn的多项式，即

上式称为布尔函数f的代数正规型，其中a0，ai，aij，…，a12…n∈F2，⊕为F2上的加法运算。f的代数正规型中非零单项式的个数称为f的项数，所有非零单项式中变元个数的最大值称为布尔函数f的代数次数。

1.1.3 汉明重量

n维向量c=(c1，c2，…，cn)的汉明重量定义为此向量中非零元的个数，记为wt(c)，即wt(c)=#{ci|ci≠0}。

1.2 S盒主要密码学性质

1.2.1S盒平衡性

1.2.2S盒的非线性度、线性概率

1.2.3S盒的差分均匀度、差分概率

1.2.4CCZ等价

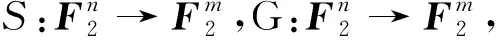
S盒一般以表的形式存储，通过查表实现调用。如果参数n和m过大，将给S盒的设计以及密码算法的实现带来困难。目前绝大多数密码算法采用8×8的S盒，简称8比特S盒。

S盒的其他密码学性质还包括：代数免疫阶、分支数、透明阶等。针对差分攻击和线性攻击这两类重要的分析方法，密码算法设计者主要考虑S盒的差分均匀度和非线性度。

2 Feistel结构的8比特S盒

目前已知硬件门数最少的8比特轻量化S盒构造方法，是SKINNY-128算法中直接基于2个4比特S盒并置构成1个新的8比特S盒[11](构造方法的结构图如图1所示)。其单轮逻辑运算涉及2个单比特或运算、2个单比特取反运算和2个单比特异或运算，迭代4轮后其差分均匀度为64、非线性度为64(即差分概率为2-2、线性概率为2-2)，与随机方式产生的8×8的S盒的差分均匀度16和非线性度96(即差分概率为2-4、线性概率为2-4)相比，差距较大。

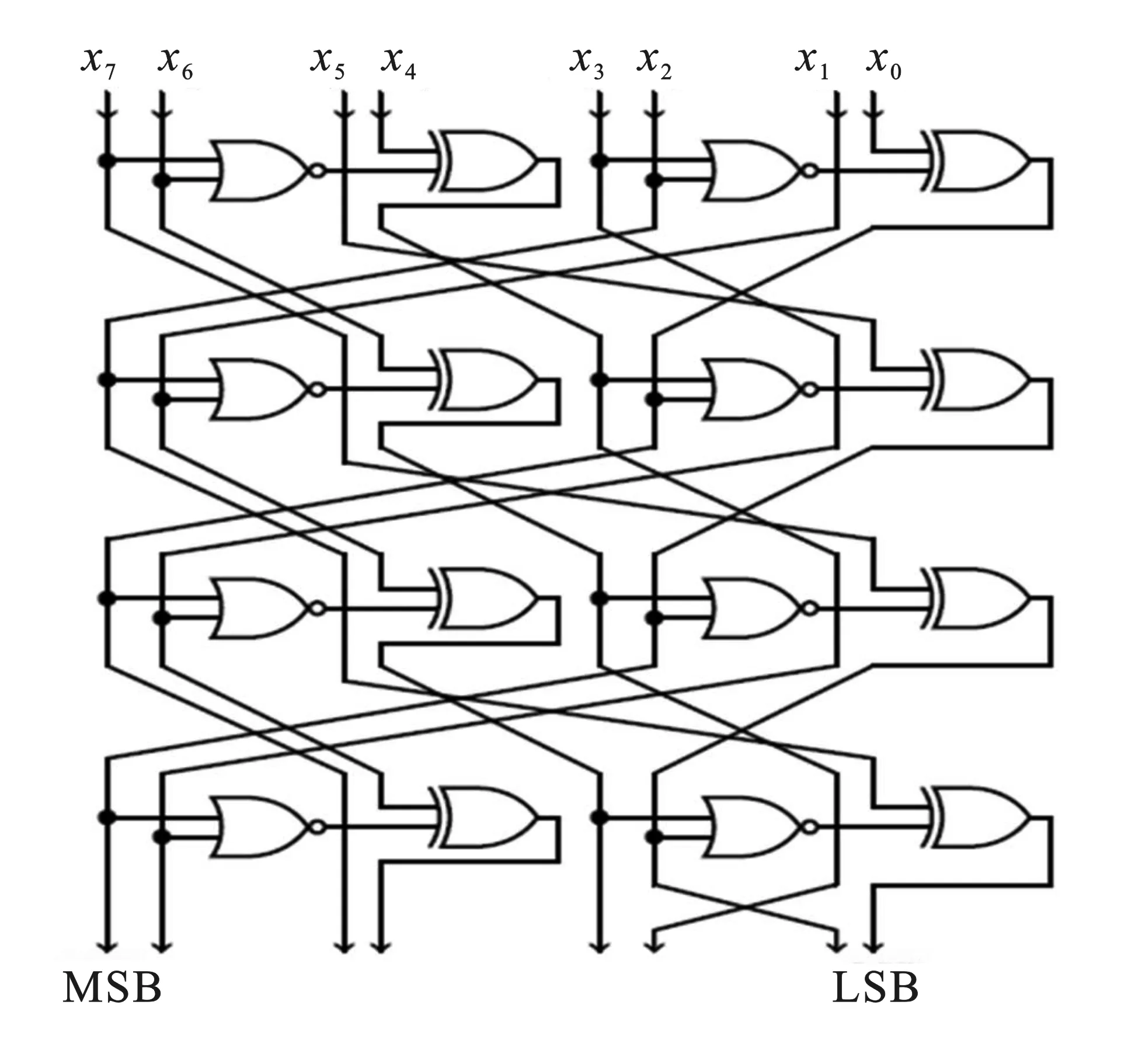
图1 SKINNY-128分组密码算法中的 8×8轻量化S盒的逻辑结构图

在图1中，SKINNY-128分组密码算法中的8比特轻量化S盒的单轮逻辑运算为

(x7，x6，x5，x4，x3，x2，x1，x0)→(x2，x1，x7，x6，x4⊕(～(x7|x6))，x0⊕(～(x3|x2))，x3，x5) ，

其中，逻辑运算符号“～”表示比特取反运算，逻辑运算符号“|”表示比特或运算。

下面介绍文中提出的一种新的8比特轻量化S盒设计方法，其单轮逻辑运算仅涉及4个比特与运算和4个比特异或运算，迭代4轮后差分均匀度为16、非线性度为96(即差分概率为2-4、线性概率为2-4)。

2.1 Feistel结构的8比特S盒设计方法

基于八分支Feistel结构的8比特轻量化S盒设计方法，其运算过程的结构图如图2所示。

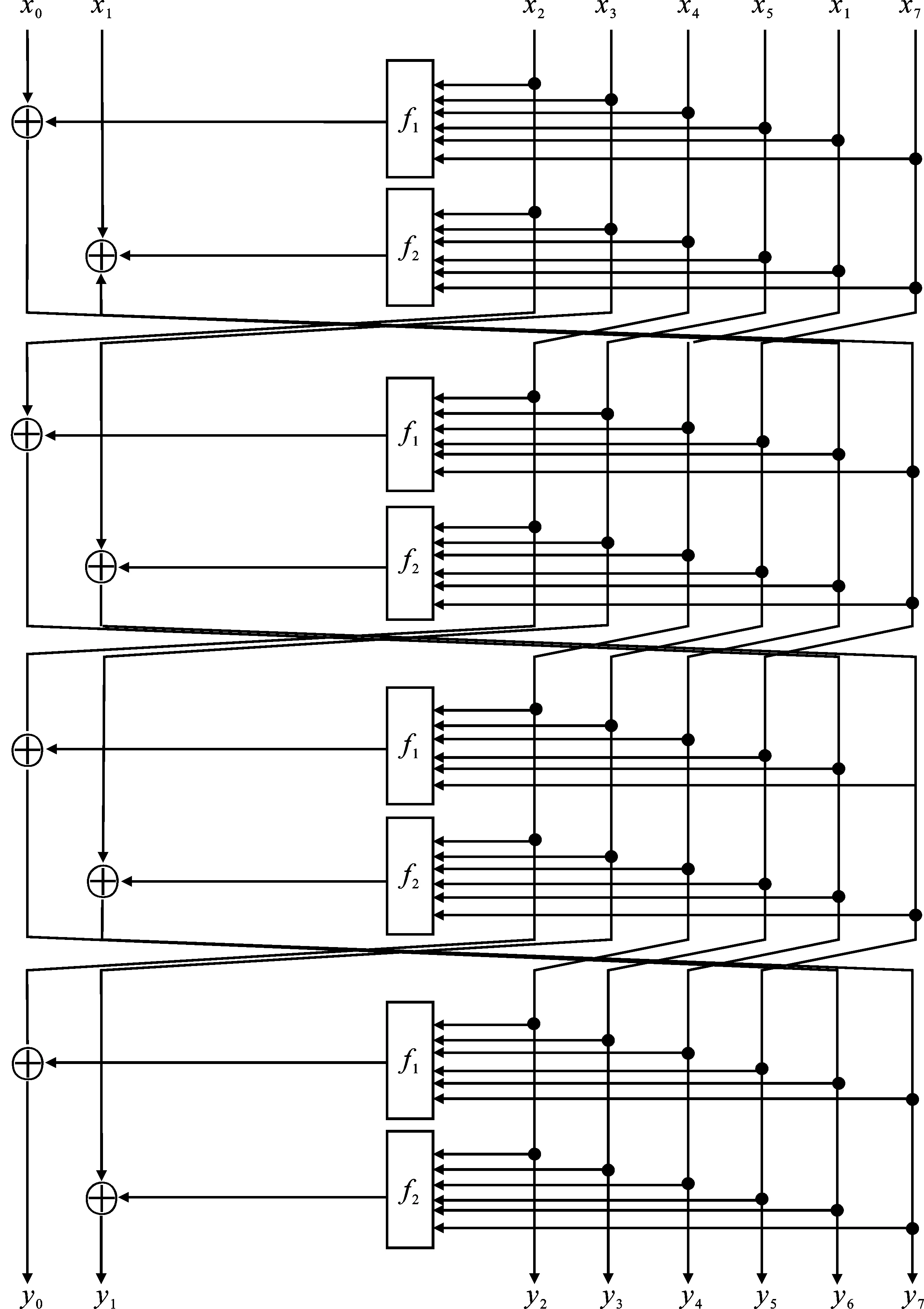
图2 基于八分支Feistel结构的8比特轻量化S盒设计方法结构图

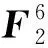
将基于八分支Feistel结构的8比特S盒设计方法记为算法1，具体运算过程如下。

算法1 S盒的8比特输入数据记为(x0，x1，x2，x3，x4，x5，x6，x7)，S盒的8比特输出数据记为(y0，y1，y2，y3，y4，y5，y6，y7)，8比特中间变量记为(t0，t1，t2，t3，t4，t5，t6，t7)，2比特中间变量记为(T0，T1)，包括步骤QS1至QS3。

QS2 对S盒的8比特输入数据(x0，x1，x2，x3，x4，x5，x6，x7)，依次遍历{0，1，…，255}所有整数值对应的8比特二元向量{(0，0，0，0，0，0，0，0)，(0，0，0，0，0，0，0，1)，…，(1，1，1，1，1，1，1，1)}，对任意整数值i∈{0，1，…，255}对应的8比特二元向量(x0，x1，x2，x3，x4，x5，x6，x7)，依次计算步骤QS21至QS25。

QS21 对输入的8比特二元向量(x0，x1，x2，x3，x4，x5，x6，x7)计算第1轮8支Feistel结构的轮变换，即t6=x0⊕f1(x2，x3，x4，x5，x6，x7)，t7=x1⊕f2(x2，x3，x4，x5，x6，x7)，t0=x2，t1=x3，t2=x4，t3=x5，t4=x6，t5=x7；

QS22 对QS21的运算结果8比特二元向量(t0，t1，t2，t3，t4，t5，t6，t7)计算第2轮8支Feistel结构的轮变换，即T0=t0⊕f1(t2，t3，t4，t5，t6，t7)，T1=t1⊕f2(t2，t3，t4，t5，t6，t7)，t0=t2，t1=t3，t2=t4，t3=t5，t4=t6，t5=t7，t6=T0，t7=T1；

QS23 对QS22的运算结果8比特二元向量(t0，t1，t2，t3，t4，t5，t6，t7)计算第3轮8支Feistel结构的轮变换，即T0=t0⊕f1(t2，t3，t4，t5，t6，t7)，T1=t1⊕f2(t2，t3，t4，t5，t6，t7)，t0=t2，t1=t3，t2=t4，t3=t5，t4=t6，t5=t7，t6=T0，t7=T1；

QS24 对QS23的运算结果8比特二元向量(t0，t1，t2，t3，t4，t5，t6，t7)计算第4轮非线性变换，即T0=t0⊕f1(t2，t3，t4，t5，t6，t7)，T1=t1⊕f2(t2，t3，t4，t5，t6，t7)；

QS25 对QS24的运算结果8比特二元向量(T0，T1，t2，t3，t4，t5，t6，t7)进行比特组合，得到8比特S盒Sbox在整数i的数值，即：y0=T0，y1=T1，y2=t2，y3=t3，y4=t4，y5=t5，y6=t6，y7=t7，Sbox(i)=y0‖y1‖y2‖y3‖y4‖y5‖y6‖y7。

QS3 输出8比特S盒Sbox，其真值表为{Sbox(0)，Sbox(1)，…，Sbox(254)，Sbox(255)}。

结论1设8比特S盒SB是由算法1产生的S盒，则SB是平衡的。

由八分支广义Feistel结构的单轮变换是置换，易知，迭代4轮后得到的SB依然是置换，即SB是平衡的。

结论2设8比特S盒SB是由算法1产生的S盒，则SB分量函数的代数次数大于等于2。

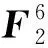
结论3设8比特S盒SB是由算法1产生的S盒，则与SB对应的f1与f2组合形式共有2114-258+1种。

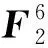
2.2 轻量化8比特S盒设计方法

考虑到适用于RFID类资源受限设备的轻量级密码算法其硬件实现资源(如等效门等)的轻量化要求，本小节对算法1中使用的f1、f2做如下限定：f1、f2的代数正规型仅包含2个2次项。

在上述限定条件下，f1共包含105种满足限定条件的可选布尔函数，f2共包含105种满足限定条件的可选布尔函数，f1与f2按照算法1中的组合情形共有11 025种。具体地，f1与f2经限定后具有如下形式：

f1(x2，x3，x4，x5，x6，x7)=(C0&x2&x3)⊕ (C1&x2&x4)⊕ (C2&x2&x5)⊕ (C3&x2&x6)⊕ (C4&x2&x7)⊕ (C5&x3&x4)⊕ (C6&x3&x5)⊕ (C7&x3&x6)⊕ (C8&x3&x7)⊕ (C9&x4&x5)⊕ (C10&x4&x6)⊕ (C11&x4&x7)⊕ (C12&x5&x6)⊕ (C13&x5&x7)⊕ (C14&x6&x7)；

f2(x2，x3，x4，x5，x6，x7)=(D0&x2&x3)⊕(D1&x2&x4)⊕(D2&x2&x5)⊕(D3&x2&x6)⊕(D4&x2&x7)⊕(D5&x3&x4)⊕(D6&x3&x5)⊕(D7&x3&x6)⊕ (D8&x3&x7)⊕ (D9&x4&x5)⊕ (D10&x4&x6)⊕ (D11&x4&x7)⊕ (D12&x5&x6)⊕ (D13&x5&x7)⊕ (D14&x6&x7)；

通过计算机程序搜索，在f1、f2的代数正规型仅包含2个2次项的限定条件下，根据算法1共找到了52个新的8比特轻量化S盒，其单轮逻辑运算仅涉及4个与运算(单比特)和4个异或运算(单比特)，经过4轮迭代后，这52个新的8比特S盒的差分均匀度为16、非线性度为96(即差分概率为2-4、线性概率为2-4)。f1、f2代数正规型仅包含2个2次项时，密码性质好的52个8比特S盒对应的向量C、D的具体结果如表1所示。

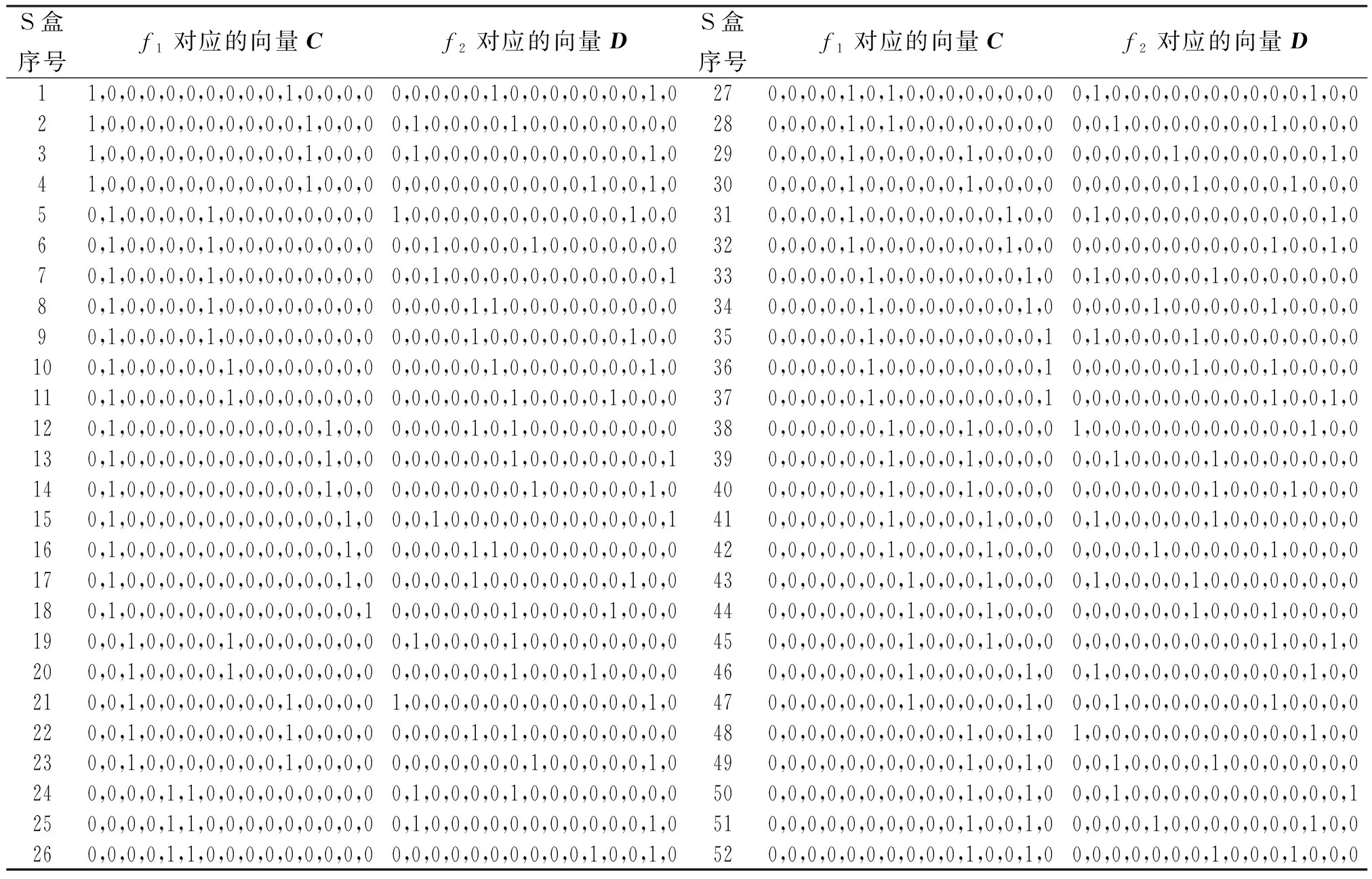
表1 52个8比特S盒对应的f1、f2代数正规型

定理1设8比特S盒LW_SB是由算法1产生的表1中的52个S盒中的任意一个，则LW_SB具有如下密码学性质：

(1) LW_SB是平衡的；

(2) LW_SB的分量函数的代数次数至少为2，至多为6；

(3) LW_SB的非线性度大于等于96；

(4) LW_SB的差分均匀度小于等于16。

证明：性质(1)、(2)由结论1、结论2容易得到，性质(2)、性质(3)、性质(4)可通过测试上述52个S盒得到。

8比特S盒LW_SB与目前已知硬件门数最少的8比特轻量化S盒(SKINNY-128算法中基于2个4×4的S盒并置构成的S盒)[11]相比，具有如下显著优势：

(1) 其单轮逻辑运算涉及4个单比特与运算和4个单比特异或运算，与SKINNY-128算法中S盒硬件实现资源相当；

(2) 其差分均匀度为16、非线性度为96，即差分概率为2-4、线性概率为2-4、分量函数代数次数达到6，优于SKINNY-128算法中S盒的密码性质(即差分概率为2-2、线性概率为2-2、分量函数代数次数达到6)。

2.3 轻量化8比特S盒的CCZ等价类分布

利用2.2节轻量化8比特S盒的设计方法，共得到52个新的8比特轻量化S盒，其单轮逻辑运算仅涉及4个单比特与运算和4个单比特异或运算，经过4轮迭代后，这52个新的8比特S盒的差分均匀度为16、非线性度为96。

更进一步，文中研究了表1中52个新的8比特轻量化S盒的CCZ等价类分布。首先将8比特S盒转化为有限域上线性码的生成矩阵，再利用数学软件magma判定不同线性码之间的等价性，从而判定不同8比特S盒之间的CCZ等价性。

研究结果表明，上述52个轻量化S盒属于13个不同的CCZ等价类，每个CCZ等价类包含4个S盒。CCZ等价类分布如表2所示。

表2中S盒序号对应的列(第2列、第4列、第6列和第8列)包含的数字i(i=1，2，…，52)分别表示表1中第i行向量C、D对应的f1、f2通过算法1得到的8比特S盒。

2.4 轻量化8比特S盒的应用

笔者设计的8比特轻量化S盒在硬件实现资源小的条件下达到已知最优的差分均匀度和非线性度，同时适用于BitSlice等运算方式，在8位、16位、32位、64位等不同实现平台上具有良好的兼容性和易移植性，能够广泛应用于对称密码算法设计中。

如果将文中设计的8比特轻量化S盒用于SKINNY-128算法[11]，即直接替换SKINNY-128算法中8比特轻量化S盒，不会增加SKINNY-128算法的硬件实现资源，同时能大幅降低SKINNY-128算法抵抗差分攻击、线性攻击、相关TWEAKEY攻击的安全界轮数，具体为

(1) 抵抗差分攻击与线性攻击的安全界轮数将从15轮降低为8轮；

(2) 对应TWEAKEY比特长度128、256、384三种情况，抵抗相关TWEAKEY攻击的安全界轮数将分别从19轮降低为11轮、从22轮降低为15轮、从26轮降低为18轮。

3 结束语

笔者提出了一种新的8比特轻量化S盒设计方法，其单轮逻辑运算仅涉及4个比特与运算和4个比特异或运算，迭代4轮后得到的S盒其差分均匀度为16、非线性度为96、分量函数的代数次数能达到6且整体平衡。与目前已有的轻量化S盒设计方法相比，笔者设计的8比特轻量化S盒在硬件实现资源小的条件下达到已知最优的差分均匀度和非线性度，同时具有较高的代数次数，特别适用于设计高安全强度的轻量化密码算法。