环LWE上高效的多密钥全同态加密方案

车小亮，周昊楠，杨晓元，周潭平，刘龙飞，李宁波

(1.武警工程大学 密码工程学院，陕西 西安 710086；2.网络和信息安全武警部队重点实验室，陕西 西安710086)

LOPEZ-ALT等[1]首次提出了多密钥全同态加密(Multi-Key Fully Homomorphic Encryption，MKFHE)的概念，它支持对不同用户(不同密钥)的密文进行任意的同态运算，且运算之后的结果由参与计算的所有用户联合解密，可用于安全多方计算[2]、隐私保护[3-4]等场景，具有重要的理论研究价值和应用价值。

LTV12方案是基于NTRU密码体制设计的首个MKFHE方案[1]，之后DORÖZ等对其全同态运算进行了优化，提出了DHS16方案[5]。CHONGCHITMATE等基于此类型的MKFHE构造了具有电路隐私特性的三轮动态安全多方计算协议的CO17方案[6]。CHE等利用比特丢弃技术和密文维度扩展方法构造了一类无需密钥交换的NTRU型多密钥全同态加密方案[7]。这些NTRU型MKFHE方案，密文量和密钥量相对较少，加解密速度快，但其安全性是基于多项式环上的非标准性假设，并且无法构造高效的联合解密协议，实际应用受限。2015年，CLEAR和MCGOLDRICK根据GSW13方案[8]提出了首个基于LWE问题的GSW(Gentry-Sahai-Waters)型MKFHE方案CM15[9]，给出了从GSW型FHE到MKFHE的转化模式。2016年，MUKHERJEE等简化了CM15方案，提出了满足一轮门限解密协议的MW16方案[10]。同年，PEIKERT等提出了满足多跳(multi-hop)功能的PS16方案[11]，BRAKERSHI等进一步缩减了密文的增长规模，提出了全动态(fully dynamic)的BP16方案[12]。这些GSW型MKFHE方案安全性高，运算过程无需进行密钥交换，但密文规模随用户数量增长较快，加解密速度较慢、同态运算效率不高。2016年亚密会上，CHILLOTTI等基于GSW13方案在T=(0，1]环上的变种TGSW，构造了全同态方案CGGI16[13]，具体呈现了全同态方案自举过程的运算效率，并于2017年编写了全同态加密软件库TFHE[14]。2019年，CHEN等将TFHE框架与MKFHE结合，提出了一种TFHE型MKFHE方案CCS19[15]。但该类方案不支持打包技术，从而导致密文扩展率较大。BGV(Brakerski-Gentry-Vaikuntanathan)型MKFHE安全性基于RLWE问题，支持并行加速和密文打包技术，可实现MKFHE的快速运算。2017年，CHEN等利用环上的GSW加密方案来生成密钥转化过程所需的计算密钥，提出了首个BGV型多跳MKFHE方案CZW17[16]。2019年，LI等利用RBGV和RGSW密文之间的混合同态乘法生成计算密钥，将CZW17方案中BGV和GSW扩展密文的尺寸缩减了近一半，设计了层级的BGV型MKFHE方案LZY+19[17]。同年，CHEN等在CKKS17[18]方案和LZY+19方案的基础上，优化了重线性化过程，构造了高效的多密钥同态加密方案CDKS19[19]，并将该方案应用于神经网络的隐私计算。但该类方案的密文规模随用户数量呈线性增长，设计全同态加密方案时生成计算密钥量大，算法效率有待提高。

笔者通过减小密文量和密钥量，简化计算密钥生成过程，来提高BGV型多密钥全同态加密方案同态运算效率。首先，优化了计算密钥的生成算法，降低了公钥尺寸，缩减了生成计算密钥的密文扩展规模；其次，引入了低位比特丢弃技术，降低了因比特分解计算产生的冗余，提高了运算效率；最后，根据优化的算法，结合低位比特丢弃技术，调整公钥和计算密钥的生成方式，构造了高效的BGV型MKFHE方案。

1 相关知识与关键技术

1.1 困难问题

基于环上的误差学习问题(Ring Learning With Errors，RLWE)：对于安全参数λ，定义维度n=n(λ)，d=d(λ)为2的幂次，模数q=q(λ)≥2为素数，定义多项式环R=[X]/xd+1和Rq=R/qR，以及R上的错误分布χ=χ(λ)，环上误差学习问题就是区分以下两个分布是困难的：①均匀选取②选取其中

1.2 关键技术

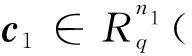
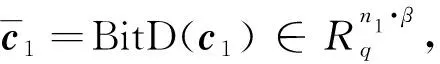
1.3 BGV型多密钥同态加密的密文扩展算法

构造计算密钥生成算法，需要引入BGV型MKFHE密文扩展算法。根据LZY+19方案的定义，BGV型MKFHE的密文扩展算法RBGV简述如下。

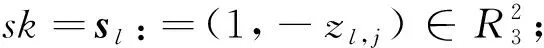
(4) RBGV.CTExt(c，K′)：定义密文组ct={c，K，l}，其中K表示密文c对应的用户集合，l表示密文c对应的电路层级信息。设用户集K={i1，…，ik}和K′={j1，…，jk'}，K⊂K′。

2 计算密钥生成算法的优化

本节通过选取合适的共用随机变量参数，缩减公钥和计算密钥密文的尺寸规模，并利用低位比特丢弃技术，构造一种效率更高的计算密钥生成算法。

2.1 计算密钥密文的生成

2.1.1 生成用户的密钥信息

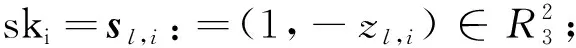
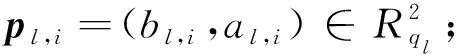
2.1.2 生成计算密钥的密文

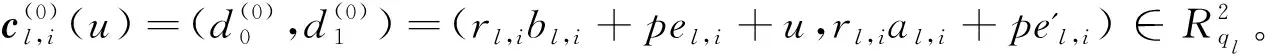
2.1.3 构造辅助密文

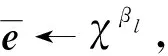
2.2 计算密钥密文的扩展运算

为了降低辅助密文di，1的维度，定义一个检索函数。

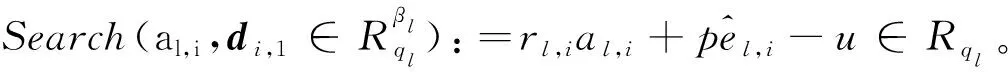
2.2.1 密文扩展运算

对于2个用户i，j而言，使用j的公钥pl，j=(bl，j，al，j)对用户i的计算密钥密文进行扩展运算，具体如下：

步骤1 将用户i的辅助密文di，0附加用户j的部分公钥信息bl，j，得到

步骤3 根据用户j的部分公钥信息al，j，执行检索函数，得到

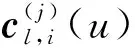
(1)

2.2.2 正确性验证

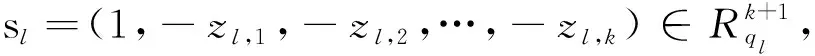
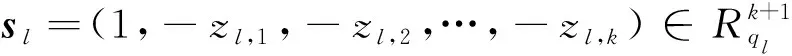
(2)

2.3 低位比特丢弃技术的应用

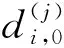
2.3.1 低位比特丢弃技术的正确性

(3)

2.3.2 满足正确性的条件

(4)

根据式(3)和式(4)，满足低位比特丢弃技术应用的正确性，则要使下式成立：

(5)

2.4 计算密钥的生成算法

本节重新设定了初始参数，将低位比特丢弃技术应用于计算密钥的密文扩展运算，构造了基于环上的低维密文扩展算法。并将该算法与RBGV密文算法进行混合同态乘法运算，构造出计算密钥的生成算法。

2.4.1 密文扩展算法

用RLDA表示构造的基于环上的低维密文扩展算法(Ring-based Expansion Algorithm with Low Dimension)，具体如下：

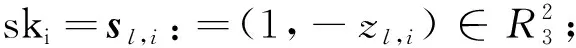
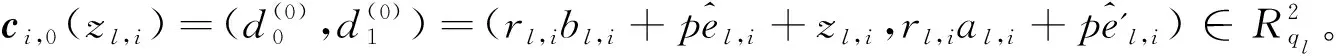
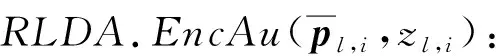
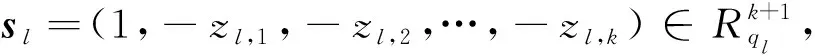
2.4.2 优化的计算密钥生成算法

利用RBGV密文扩展算法和RLDA算法进行混合同态乘法运算，得到优化的计算密钥生成算法。

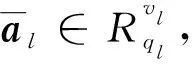
对Φl，j[t]，Ψl，i[t']分别进行密文扩展，可得

(6)

(7)

2.5 算法性能分析

文中构造的计算密钥生成算法，主要是降低了用户的公钥尺寸，缩减了计算密钥的密文扩展维度。相对于LZY+19方案和CDKS19方案中的计算密钥生成算法，其公钥尺寸、计算密钥的密文尺寸和扩展密文尺寸呈倍数降低，具体对比如表1所示。

表1 文中构造的计算密钥生成算法与LZY+19和CDKS19的算法存储开销对比

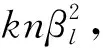
3 高效的BGV型MKFHE方案的构造

根据优化的算法，并结合模交换技术和密钥交换技术，构造了层级的BGV型多密钥全同态加密方案。

3.1 方案构造

(1) MKFHE.Setup(1λ，1K，1L)：安全参数为λ，电路层数为l∈{L，…，0}，用户数集为K，多项式环R=[X]/Φm和Rq=R/(qR)，R上的错误分布χ=χ(λ)的界为B。每一层电路的模数qL≫qL-1≫…≫q0，小整数p与所有的模数互质。令βl=logql+1，设比特丢弃长度为κ<β0，对任意l∈{L，…，0}均满足vl=βl-κ。选择L+1个随机公共向量输出公共参数

(2) MKFHE.KeyGen(pp)：输入公共参数pp，m∈{κ+1，κ+2，…，βl}，生成第j个参与方所需要的密钥(j∈[K])。

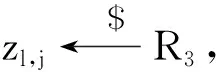
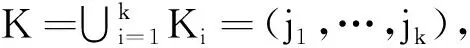
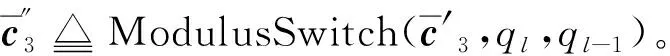
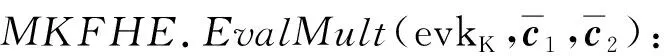
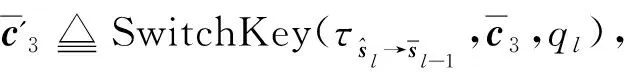
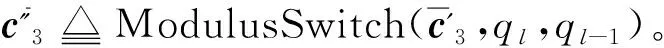
3.2 方案分析

3.2.1 安全性分析

3.2.2 噪声分析

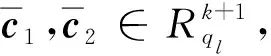
DBitD(ciξ，iξ′)=((ciξ，iξ′)κ+1，(ciξ，iξ′)κ+2，…，(ciξ，iξ′)βl) 。

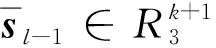
(8)

设比特丢弃长度取最大值κmax，此时因低位比特丢弃技术而产生的噪声值最大。根据式(2)可得‖eM‖

(9)

因为‖eB‖小于‖eM‖，所以

3.2.3 效率分析

因为CDKS19方案是非层级的多密钥全同态加密方案，而笔者构造的方案是层级的多密钥全同态加密方案。在效率分析中，与层级的BGV型MKFHE方案LZY+19进行对比，构造的方案进一步简化了计算密钥的生成过程，并且利用低位比特丢弃技术，降低了计算冗余。以在l层完成一次同态乘法运算为例，文中方案的扩展密文尺寸、公钥尺寸、生成计算密钥的中间密文尺寸和产生的噪声值等参数与LZY+19方案的对比如表2所示。

表2 文中方案与LZY+19方案的参数对比

由表2可知，扩展密文的尺寸相对于LZY+19方案没有改变，但公钥尺寸缩小了至少一半，生成计算密钥的中间密文尺寸约减小为LZY+19方案的1/3，且产生的噪声值是关于n的倍数降低。此外，文中方案引入了比特丢弃技术，计算的复杂性相对较低，所以笔者构造方案的效率高于LZY+19方案的效率。

4 结束语

笔者设计了一种更高效的BGV型MKFHE方案，满足IND-CPA安全。相对于现有的方案，设计的新方案简化了计算密钥的生成过程，缩减了密钥的尺寸，并利用低位比特丢弃技术，减小了计算冗余，使得同态运算效率得到提高。下一步，将针对如何减小方案中密文的尺寸，进一步提高同态运算效率继续展开研究。