低复杂度的增强图像来源检测算法
2021-01-29王俊祥倪江群
王俊祥,黄 霖,张 影,倪江群,林 朗
(1.景德镇陶瓷大学 机械电子工程学院,江西 景德镇 333403;2.中山大学 数据科学与计算机学院,广东 广州 510006;3.东南数字经济发展研究院,浙江 衢州 324000)
随着多媒体技术的飞速发展,数字图像已被广泛运用于人们的生活之中。随之,数字图像处理技术也获得了较好的发展。在此过程中,作为最常规的数字图像处理技术,对比度增强算法常用于改善数字图像的视觉质量,例如增强原本不清晰的图像、凸显图像中感兴趣区域等。与此同时笔者发现,当前很多手机拍摄的图片、美颜照片均在一定程度上进行了图像增强操作,如伽马矫正和滤镜等。目前已有多种图像增强算法[1-2],如冯玉颖等人[1]提出的基于新模型的图像增强新算法更加符合人眼视觉模型,以及当前主流的空域常规对比度增强算法等,如直方图均匀化[3]、伽马矫正等。
近年来WU等人[4-5]提出另一种具有对比度增强效果的可逆信息隐藏算法(Reversible Date Hiding-Contrast Enhancement,RDH_CE)。此类算法在往载体中嵌入一定比例的秘密信息后,可生成与常规图像增强算法视觉效果一致的含密增强图像,如图1所示。此特点为后续不分辨增强图像来源而直接使用的操作带来了巨大安全隐患,例如RDH_CE可嵌入具有隐私窃取功能的代码,并伪装成常规增强图像供用户使用。基于此,设计一种能够有效检测RDH_CE类别图像的增强图像来源检测算法至关重要。
据课题组检索可知,目前的图像检测算法(或称为取证算法)主要分为如下两类:① 基于图像内容基本保持的常规图像检测算法。此类算法主要用于判断图像是否经过具有图像内容保持功能的篡改操作(如重采样[6]、压缩[7-8]、中值滤波[9-10]以及剪切和复制粘贴[11-13]等),以保证对给定图像的安全使用;② 基于图像增强效果的检测算法。目前该类算法[14-19]主要用于鉴别给定图像是否经过了常规增强操作(如直方图均匀化、伽马校正等)的篡改处理,以保证使用图像的真实可靠。文献[14] 通过证明常规对比度增强图像的能量高于原始图像的,且能量主要集中在高频部分的结论,设计了基于高频能量特征的有效检测算法。文献[15]通过分析对比度增强前后像素直方图在最高频率峰值点和零频率点上的区别,给出了简单的基于直方图零点个数的计数特征进行常规增强图像的检测。为进一步提高检测精度,文献[16]提出了基于二阶统计特征——灰度共生矩阵的特征设计思路。实验结果表明,借助该特征可以更好地表征对比度增强操作所留下的痕迹,同时相关痕迹不易被反检测算法去除。然而,此类算法的特征计算复杂度较高。近期,文献[17]在文献[16]的基础上提出了基于灰度共生矩阵的卷积神经网络(Convolutional Neural Networks,CNN)检测框架。该算法一方面借鉴了文献[16]给出的图像灰度共生矩阵在增强图像表征方面的优势,另一方面通过CNN卷积神经网络在特征学习和图像分类方面的强大功能,进一步提升了增强图像的检测能力。但是此类基于神经网络的检测方法需要大量的数据,且计算复杂度偏高。
综上所述,目前的增强图像检测算法主要研究常规对比度增强图像和原始图像间的区别。然而,笔者主要关注RDH_CE与常规增强图像(直方图平移、伽马校正等)的检测。目前,针对此类新场景下的检测算法未有涉及。另外,鉴于常规增强图像检测算法没有考虑到RDH_CE自身的执行特点,因此直接用于RDH_CE新场景时检测效果不佳,尤其是在多种对比度增强图像混合的情况下(即存在RDH_CE和多种常规增强图像混合的场景)。基于此,笔者通过对RDH_CE和常规对比度增强算法执行特点的分析,设计了多个适合于表征其间区别的特征,如直方图的零点个数、零点分布情况和直方图包络线等,并用于新场景下(含RDH_CE图像)的对比度增强图像来源检测。实验结果表明,较之同类其他检测算法,笔者提出的算法不仅能够有效地检测到RDH_CE图像,还能够有效区分多种不同的常规增强图像来源。
1 多种对比度增强图像的执行特点分析
此章节主要分析RDH_CE与多种常规增强图像(如直方图均匀化、伽马矫正)各自的执行特点,并总结其间的区别,用于后续的检测特征设计。
1.1 具有对比度增强效果的可逆信息隐藏算法
笔者以WU等人[5]为例,分析此类具有对比度增强效果的可逆信息隐藏算法的执行特点,具体说明如下。如图2所示,此类算法包含如下几个步骤:
(1)计算图像的像素直方图,记为h(x)。
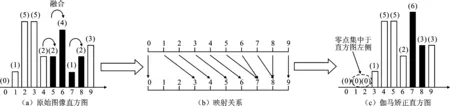
(2)扫描整个直方图,找出直方图中的零点(即频率高度为零的点),并将零点平移到直方图的最外侧。如果没有零点,则通过融合两个相邻且频率高度最低的点来产生新的零点,如图2(a)所示。
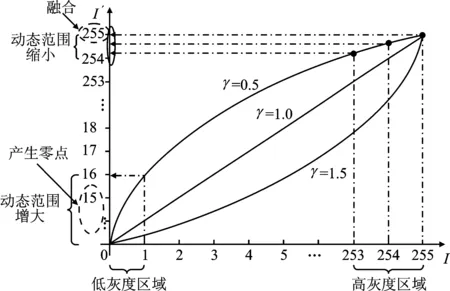
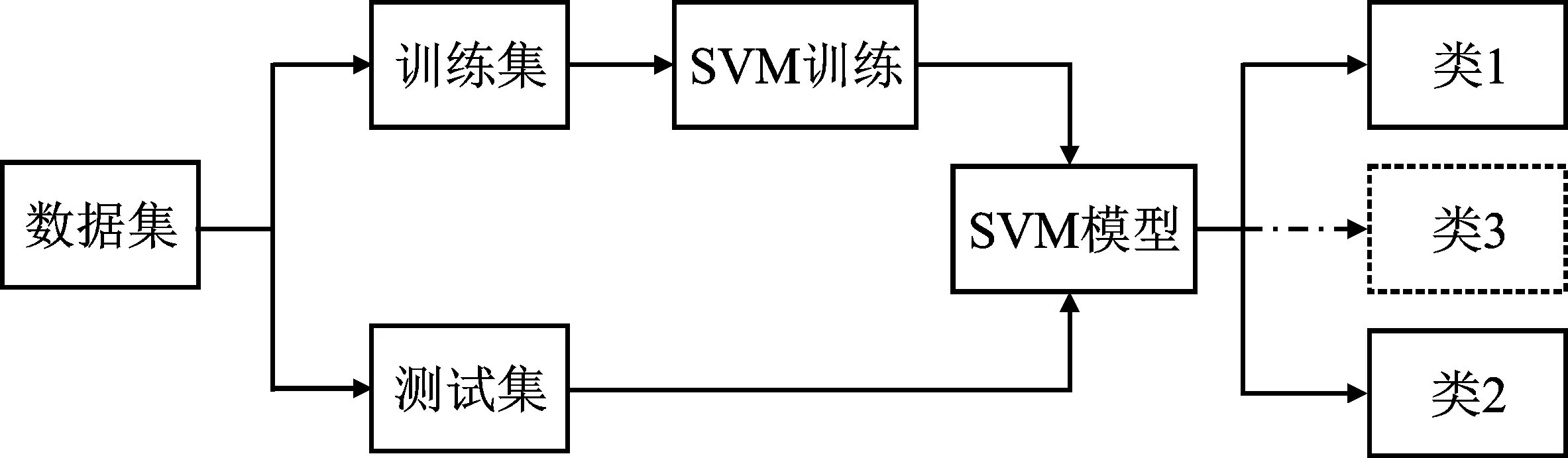
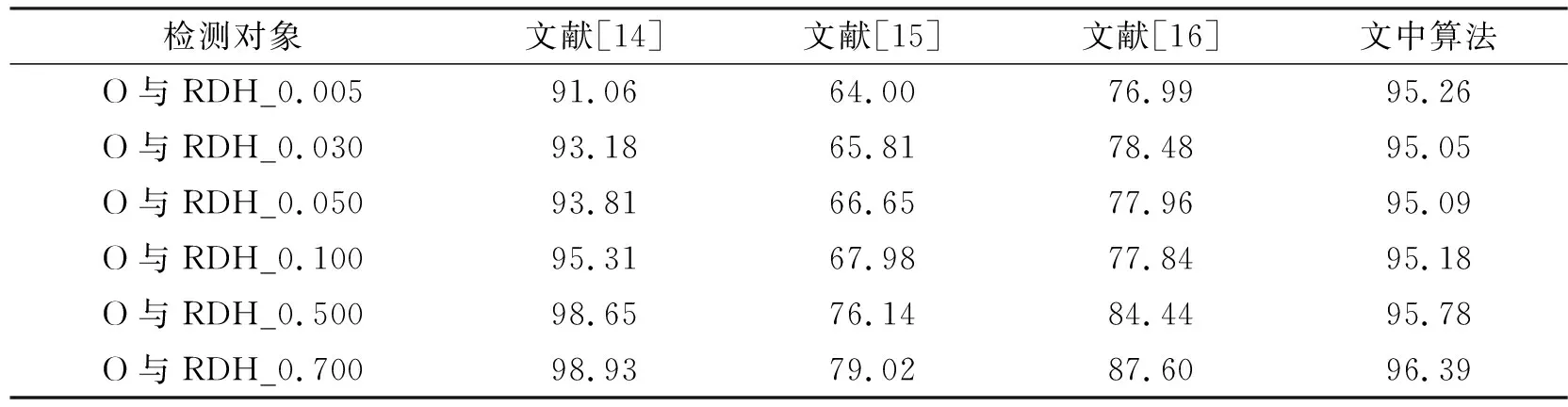
(3)选择两个峰值点(即直方图中最高的点),分别记为Pl和Pr,(其中Pl (1) 其中,x和x′分别表示原始像素和嵌入秘密信息后的含密像素,b表示1 bit嵌入信息。考虑到秘密信息常为0、1均匀分布的比特流,所以生成的直方图柱一般为峰值点柱均匀折半后的效果,如图2(b)和图2(c),以表示分别嵌入0和1。 显然,上述操作一方面不断地消耗直方图中的零点(或低频率点),另一方面信息的嵌入操作会导致对高频率点的折半操作。通过重复上述过程,可使直方图趋向于均匀化,达到对比度增强的效果。 综上所述,可以认为此类RDH_CE算法在实现图像增强的同时具备如下特征:①零点个数逐步减少;②直方图柱的高度逐步降低,使得直方图包络线趋于均匀化。 1.2.1 直方图均匀化 一般直方图均匀化[3]的过程包含如下步骤: (1)计算图片I的像素直方图h(i)。 (2)直方图归一化,并计算累计分布概率。具体计算为 (2) (3) 其中,N表示图像的像素个数,i表示直方图的横坐标即像素的灰度值。 借助直方图累计分布,构建映射关系,可获得均匀化后的直方图。具体可参考文献[3],其中映射关系g即为直方图累计分布概率乘以最大的灰度值,可表示为 g=round(255ha(i)),i∈[0,255] 。 (4) 如图3所示,由上述直方图均匀化操作过程,可以获得一个“多对一”的映射关系如图3(b),即通过对原始直方图中多个低高度直方图柱堆叠(或称融合),以获得一个较之原始直方图(如图3(a))更为均匀的结果(如图3(c)),并以此实现直方图的均匀化和视觉增强效果。 显然,直方图均匀化过程具有如下特点:① 直方图柱融合(多对一的结果)趋向于将高度较低的直方图柱进行堆叠,并生成新的零点,即零点个数增加;② 高直方图柱不存在类似于1.1节中发生的折半情况,所以直方图柱相比原始值不会发生高度降低的现象。 1.2.2 伽马矫正 伽马矫正的原理如下: (1)首先,对图像I进行归一化操作(即每个像素都同时除以255),得到归一化图像IN。 (2)对归一化图像IN进行伽马矫正,公式如下: IE=(IN)γ。 (5) (3)对伽马矫正后的图像IE进行反归一化操作(即每个像素同时乘上255),再四舍五入取整得到最终伽马增强图像I′。 图4给出了伽马矫正参数γ=0.5的示意图。由映射关系可知,在低灰度区域(靠近0值)会增加零点,在高灰度区域存在直方图堆叠现象。 图4 伽马矫正示意图 图5 伽马矫正映射曲线 图5给出了不同γ值下的直方图映射关系说明,用于简单说明直方图的变化特点。显然,当γ=0.5<1.0时,低灰度区域的动态范围增大,而高灰度区域的动态范围变小。在灰度值动态范围增大的情况下,原始像素出现拉伸,因此会生成新的零点。如图5所示,原始灰度值0和1在进行伽马校正过程中分别被映射为0和15.96,经过取整操作转换为0和16,因此伽马校正后的图像会产生15个零点(灰度值分别为1,2,3,…,15);同理,在灰度值动态范围变小的区域,会出现像素值的融合现象,即直方图柱的堆叠融合,并伴随出现直方图包络线的单峰产生。如图5中横坐标显示的灰度值254与255经过映射关系分别转换为纵坐标的254.5和255,伽马矫正会对灰度值进行取整操作,因此254.5映射为255,即原始图像中灰度值为254与255的点经过伽马矫正后均映射为255,出现融合现象。当γ>1时,则恰好相反,低灰度区域动态范围变小,高灰度区域动态范围变大,会出现低灰度区域堆叠,高灰度区域零点现象。 基于此,伽马矫正特点概括如下:① 存在直方图堆叠,直方图零点个数增加的现象;② 零点分布集中于直方图一侧(灰度区域动态范围增大侧),直方图柱包络线出现单峰的现象(靠近灰度区域动态范围减小侧)。 综上所述,3种不同对比度增强算法的执行特点与区别可概括如表1所示。 表1 3种增强方法的执行特点分析 基于上述分析可知,不同类别的增强图像区别集中在:①直方图零点的个数及分布情况;②直方图包络线的变化。基于此,笔者设计了4个有效特征进行表征,记为F={fi|i∈[1,4]}。 (1)特征1直方图的零点个数记为f1。直方图的零点个数表示直方图中频率高度为0的直方图柱个数,即 (6) 其中,C(•)表示计数函数。如果其中h(i)=0为真,则C(h(i)=0)等于1;否则,C(h(i)=0)等于0。 (2)特征2直方图的零点分布记为f2。考虑到不同图像增强算法对零点分布的影响(如直方图均匀化生成的零点分布相对均匀,伽马矫正产生的零点一般集中在直方图单侧,RDH_CE算法通常优先消耗位于直方图中间的零点,并剩余直方图两侧的零点),本部分设计了一个表征直方图零点分布的特征参数如下。 首先,记录直方图中频率高度不为零的直方图柱横坐标位置,得到一个位置数列,记为L=[l1,l2,…,lN];然后,计算相邻元素间的距离,并计算这些距离的平均值表征零点分布情况。具体计算如下: (7) 其中,|•|表示绝对值函数。 (3)特征3直方图中非零点的均值残差标准差记为f3。此特征用于表征直方图包络线的差异,具体计算思路如下。 (8) (4)特征4直方图相邻非零点的标准差记为f4。考虑到不同增强算法导致邻近直方图柱陡峭程度存在区别的情况,此特征作为补充参数,辅助表征直方图包络线的差异。具体计算过程如下。 首先,得到直方图非零点的高度数列H=[h1,h2,…,hK];然后,计算数列H中相邻元素间的差值绝对值,记为数列D_H={d_hi|i∈[i,K-1]},其中d_hi=|h(i+1)-hi|;最后,计算D_H的标准差,即 (9) 基于上述特征,F={fi|i∈[1,4]},笔者采用适合于低维特征的高效分类算法(Support Vector Machine,SVM)进行增强图像的来源检测。如图6所示,首先,将数据集分为训练集与测试集两类;然后,用训练集训练一个SVM分类模型,笔者拟采用LIBSVM[20]进行实现。在训练过程中涉及两个超参数(惩罚因子c和核参数g)的优化问题,其决定了分类器的分类准确率和泛化能力。其中惩罚因子c表征对误差的宽容度,核参数g所选核函数自带的参数。笔者使用交叉验证方法进行上述超参数的优化。在交叉验证中,c和g的范围分别为[2-2,24]和[2-4,24],步长为0.5;最后,将测试集输入到训练好的模型中进行分类检测。另外,需要说明:LIBSVM可以按照二分类和三分类两种模式进行,其中二分类表示仅需要区分RDH_CE图像和常规的图像增强图像。如果需要进一步判断当前常规图像来源于何种常规增强方式,可选择三分类,即增加类3,如图6中虚箭线所示。 图6 SVM流程图 笔者使用BaseBoss数据集(10 000张512×512的8 bit灰度图像)[21]进行测试,并在此基础上生成三类增强图像,即10 000张直方图均匀化增强图像、10 000张伽马矫正增强图像(对应于伽马矫正参数为{0.5,0.7,0.9,1.1,1.3,1.5,2.0}的测试图像分别为1 500张,1 500张,1 500张,1 500张,1 500张,1 500张,1 000张)和给定容量下10 000张RDH_CE增强图像。需要说明,在RDH_CE增强图像构造过程中,如果存在信息无法完全嵌入的情况,则直接删除相关图像。在实验过程中保持测试集与训练集图片数量相等。 实验中原始图像记为“O”;直方图均匀化图像记为“HE”;各个参数下的伽马矫正图像记为“G_i”,其中i代表不同的伽马参数;各个容量下的可逆信息隐藏增强图像记为“RDH_k”,其中k表示嵌入容量。笔者以检测准确率表征算法检测的准确性。具体计算公式为 (10) 其中,n表示测试集中准确分类样本的数量,N表示所有样本的总数量。在三分类时,n表示测试集中每个类别图像都准确检测的总数。 笔者将实验分为:① 测试所设计特征的有效性;② 将笔者提出算法与多种典型算法[14-16]进行综合性能比较,以体现笔者提出算法的优势;③ 给出各种对比算法的计算复杂度分析。 如图7所示,给出了典型的单个特征(特征1和特征2)在检测4种图像来源方面的效果。 由图7可知,单个特征在区分不同种图像来源方面效果显著,不同种类算法出现的区域有明显的层次划分。此外,针对3种典型的对比度增强图像(直方图均匀化图像、伽马矫正图像和RDH_CE图像),表2给出了多特征组合后的检测效果。显然,随着组合特征数量的增加,检测准确率也获得明显提升,验证了笔者设计特征的有效性。后续实验均采用4个特征进行检测。 表2 不同特征组合情况下的检测准确率对比% 文中提出算法关注于多种增强图像(如RDH_CE、直方图均匀化、伽马校正等)的来源鉴别,而传统增强图像检测算法[14-16]侧重于鉴别对比度增强图像和原始图像,因此,这小节给出两种不同场景下的检测准确率对比分析,即场景1:多种增强图像来源的检测;场景2:增强图像与原始图像间的检测。 3.2.1 场景1:多种增强图像来源的检测 此小节给出了笔者提出算法与3种典型算法[14-16]在二分类和三分类情况下的对比实验。其中二分类包含2种增强图像混合来源检测(即检测对象分别为直方图均匀化图像与RDH_CE图像、伽马矫正图像与RDH_CE图像、直方图均匀化图像与伽马矫正图像),并使用ROC曲线[22]表征测试结果(其中ROC曲线右下角包含面积越大,表示性能越好,其详细介绍见文献[22]),如图8~10所示。三分类包含3种增强图像混合来源检测(即检测对象分别为直方图均匀化图像、伽马矫正图像和RDH_CE图像),并用检测准确率表征测试结果。 由图8~10观察可知,多种不同二分类检测场景下,笔者提出算法获得的ROC曲线面积基本接近于1,表明检测准确率近乎于100%。相比之下,其他3种典型算法[14-16]在多个场景下存在检测准确率不高,稳定性较差的情况。例如,在检测直方图均匀化图像与RDH_CE图像时,文献[14]的检测算法效果不佳;在检测伽马矫正图像与RDH_CE图像时,文献[14]、[15]和[16]的检测算法效果不理想;在检测直方图均匀化图像与伽马矫正图像时,文献[14]和文献[15]提出的检测算法不稳定。其原因在于文献[14]、[15]和[16]提出的检测算法均针对常规对比度增强图像和原始图像之间的区别进行设计。如文献[14]作者关注对比度增强图像会产生高频分量,但是常规伽马矫正和直方图均匀化都会导致频域直方图产生高频分量,因此在检测两种增强图像混合情况时,检测效果下降。文献[15]依据对比度增强图像直方图的零点个数比原始图像直方图零点个数多的经验进行检测,但是伽马矫正与直方图均匀化都会导致直方图零点个数增加的现象,因此在两种增强图像混合时检测效果下降。文献[16]通过二阶统计特征灰度共生矩阵来描述对比度增强操作产生的影响,相比于文献[14]和文献[15]的一阶统计特征检测效果更好。但由于文献[16]设计的特征依然是针对原始图像和增强图像间的区别给出,所以对于两种增强图像混合时检测效果低于笔者所述特征。 同理,在3种增强图像混合进行检测时,笔者提出算法检测效果依然优于其他3种典型算法,如表3所示。 图8 检测对象为直方图均匀化图像与RDH_CE图像的4种算法对比度增强检测ROC曲线 图9 检测对象为伽马矫正图像与RDH_CE图像的4种算法对比度增强检测ROC曲线 图10 检测对象为直方图均匀化图像与伽马矫正图像的4种算法对比度增强检测ROC曲线 表3 3种增强图像来源检测准确率对比% 3.2.2 场景2:增强图像与原始图像间的检测 首先,给出笔者提出算法与3种典型方案在RDH_CE与原始图像场景下的检测结果,如表4所示。 表4 原始图像与RDH_CE图像检测准确率对比% 由观察可知:所有的算法检测准确率均随着嵌入容量的提升而增大。其原因在于,随着嵌入容量的提升,导致RDH算法零点消耗增多,并使其与原始图像差距变大,易于检测。另外,不难发现,笔者提出算法在不同情况下均能保持较好的优势,稳定性强,准确率保持在95%以上。相比之下,文献[15]和文献[16]提出的检测方法主要关注常规增强方法在直方图中间产生的零点,而忽略了RDH图像的特殊性,如其直方图中的零点常分布于直方图外侧的事实,所以检测性能较低。相比之下,文献[14]提出的依据高频分量鉴别增强图像与原始图像的作法却能表现出较好的优势,因为当RDH_CE算法嵌入容量变大时,直方图包络线趋于平缓,RDH图像的高频分量会小于原始图像的高频分量,此时RDH与原始图像差距逐渐拉大,进而提升检测准确率。 另外,笔者给出了传统增强图像与原始图像场景下的检测对比实验,如表5所示。在检测直方图均匀化图像与原始图像时,几乎所有算法在此场景下均能取得较好的效果,准确率接近于1。在部分情况下,如在鉴别伽马校正参数接近1的增强图像与原始图像时,由于伽马校正参数接近于1的增强效果不明显,导致其直方图零点与直方图包络线较之原始图像变化较小,因而笔者设计的特征不能很好地描述其间的差别,即在伽马校正参数分别为0.7,0.9,1.1,1.3情况下检测性能略低。相比之下,文献[14]因关注于直方图频域特征,所以其对于伽马校正参数接近于1的微小变化相对敏感,检测效果较好。另外,文献[15]构造的孤立零点特征在个别情况下也能描述其间的差别,但是性能不稳定。 表5 常规对比度增强图像检测准确率对比% 此小节提供了4种检测算法在计算复杂度方面的对比实验。考虑到目前所有算法均可采用类似分类器进行实验的现状,笔者重点给出4种算法在特征计算方面的复杂度对比实验。其中笔者实验平台为主频为2.20 GHz的Intel(R) Core(TM)i7-8750H CPU 、内存为8 GB的PC电脑,使用软件为MATLAB 2016B。如表6所示,笔者提出算法在特征计算方面可以获得一个较低的计算复杂度,优于献[14]和文献[16]提出的算法。其主要取决于笔者设计的4个简单特征计。另外,由于献[15]的算法仅需计算一个特征,所以时间复杂度最低。 表6 特征时间计算复杂度对比 笔者针对目前增强图像来源复杂,通过视觉难以分辨,不利于增强图像安全使用的现状,给出了能够鉴别RDH_CE图像和常规增强图像来源的高效检测算法。通过分析RDH_CE与多种常规增强图像的执行特点及差异,针对性地设计了有效特征,即直方图零点个数、零点分布情况及直方图的包络线等,并借助SVM分类器,可以获得高效、准确的检测结果。实验结果表明,笔者提出的算法较之当前的主流典型方案在多个场景下均可获得较高准确率和较强稳定性,优势明显。后续将关注其他增强图像的来源检测研究。1.2 常规对比度增强算法

2 特征构造及检测框架设计
2.1 特征构造
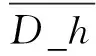
2.2 检测框架设计
3 实验结果
3.1 单特征及组合特征检测结果

3.2 综合性能对比
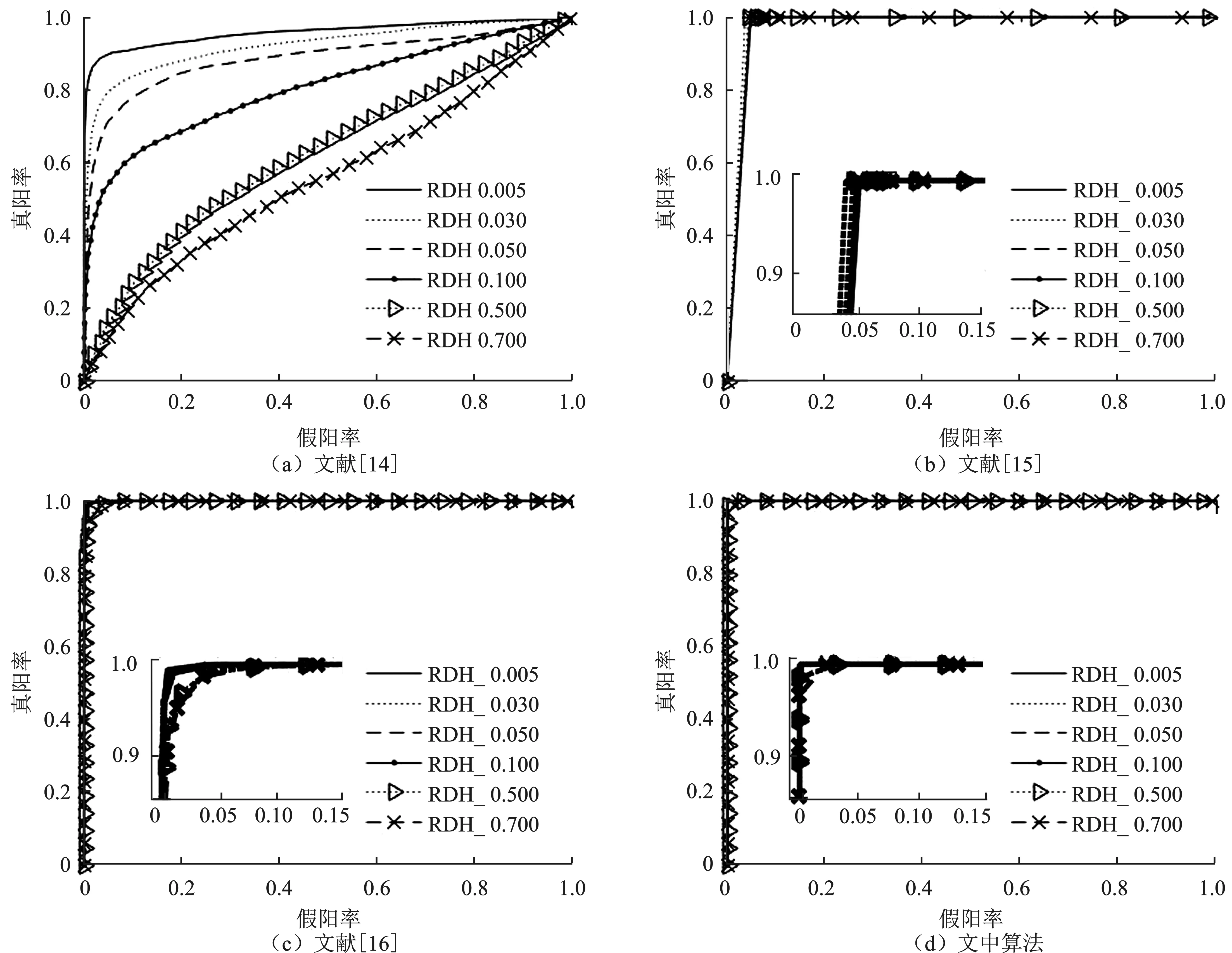


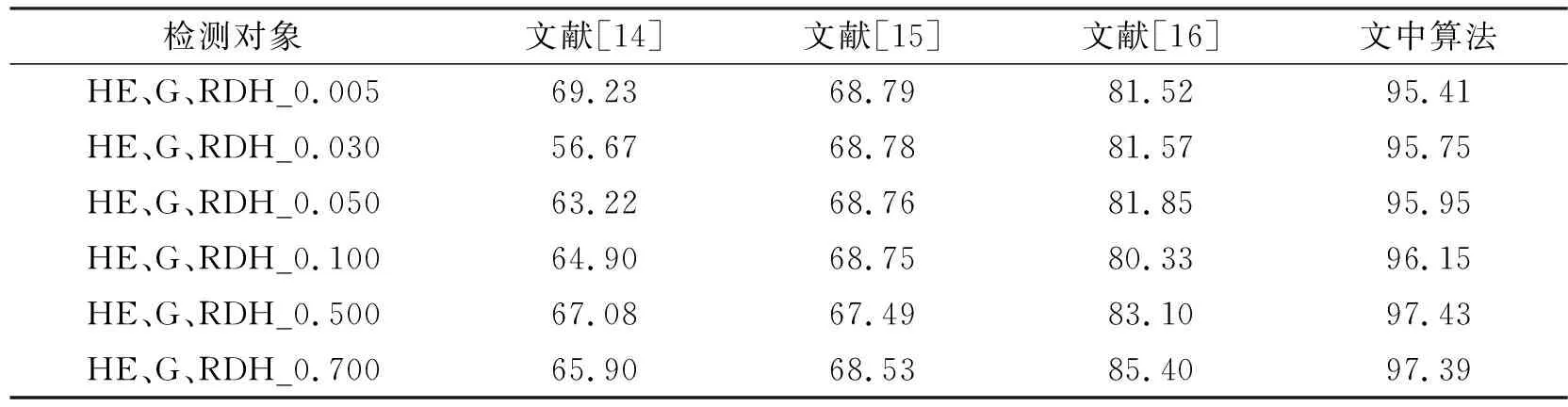

3.3 计算复杂度分析

4 结束语
