轮式移动机器人滑模轨迹跟踪控制＊

靳宇星

（新疆交通职业技术学院，新疆 乌鲁木齐 830001）

随着人工智能在21 世纪的飞速发展，越来越多的智能化机器人开始在各行各业中被应用，代替人类完成一些具有重复性、危险性的工作。其中轮式移动机器人，因其操作方便、便于运输和携带等优点在海底探测、抗震救灾、矿井勘探等领域具有广泛的应用[1]。由于其长期工作在条件较差、环境因素多变的工况下，因此对其控制性能的可靠性有较高的要求，对其控制策略的研究也一直是中外学者研究的热门话题。

轮式移动机器人传统的控制策略主要有PID 控制[2]、模糊控制[3]、反演控制[4]、非线性状态反馈控制[5]等控制策略。其中PID 控制因其算法简单易于实现等特点在工业应用中广泛存在，也是目前移动机器人应用最多的控制策略，但这种线性控制方法，在处理欠驱动问题时往往会出现响应不够快速、抗干扰能力弱的问题。因此后面的学者都将目光转向了非线性的控制策略，如滑模控制、模型预测控制等。其中滑模变结构控制具有响应快速、抗干扰能力强、对系统参数依赖性小的优点，被广泛应用在控制器的设计中，本文选取滑模控制来设计系统的控制律。

1 轮式移动机器人建模

轮式机器人的结构为前后各两个轮子，两个后轮是驱动轮为机器人本体提供动力来源，两个前轮为从动轮，为机器人本体提供支撑作用[6]。驱动轮各有一个电机，用来提供动力，当两个电机转速一致时实现前后运动，当两个电机转速存在偏差时，由于“差速”的存在从而实现机器人的转弯运动。在二维平面下其运行轨迹如图1 所示。

图1 中，X、Y代表二维平面的坐标轴，x0、y0表示移动机器人的初始位置，xd、yd表示移动机器人的给定参考位置，M为其质心位置。为了更加清晰地分析其运动轨迹，通过数学建模的方法建立其坐标轴下的数学模型。

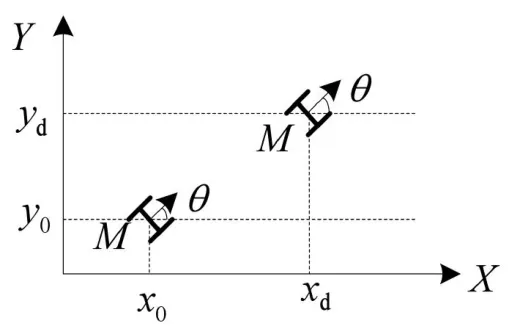
图1 轮式移动机器人的运动轨迹图

假设移动机器人的质心与其几何中心在同一点上，选取相量P=[x，y，θ]T，其中x、y分别表示机器人在X、Y轴方向的位置，θ为机器人前方向同X轴方向的夹角。选取相量W=[v，m]T，其中v、m分别表示机器人的线速度和角速度作为运动学模型的输入。由此可以将移动机器人建模如下：

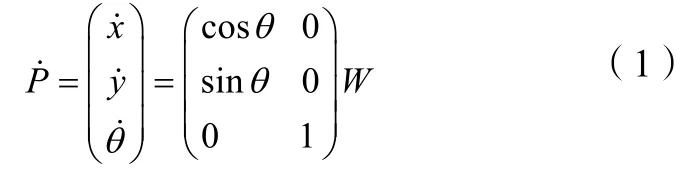
为了确保控制系统准确可靠，本文采用内外环的结构，将系统分为了位置子系统（外环）和姿态子系统（内环）的结构来分别设计控制律，系统的整体控制结构如图2 所示。

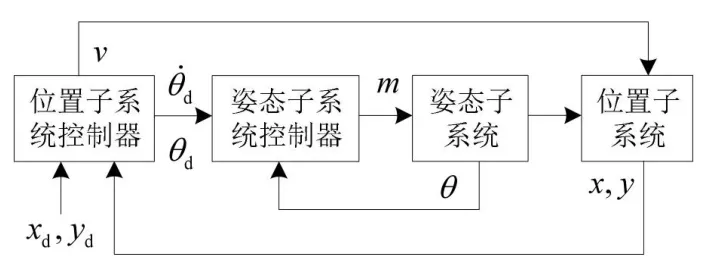
图2 基于内外环结构的控制系统框图

2 轮式移动机器人位置控制律设计

位置控制律的设计目标是使得移动机器人在二维平面的X、Y轴方向能够快速地到达给定参考点。通过设计的位置控制律，实现X、Y轴方向准确及时的跟踪，并保证前进角度θ的稳定。

则可由此设计控制律为：

根据李亚普洛夫方程可以验证系统是稳定的，跟踪误差呈指数形式收敛于0。

由vcosθ=u1、vsinθ=u2可得u1/u2=tanθ，可以看出系统机器人的前进角θ取值范围为（-90°，90°）。则可以得到满足理想跟踪轨迹的θ值为θ=arctan（u1/u2）。该角度值即为满足控制律式（3）所需要的角度。

在实际运行过程中这一角度无法满足与给定角度值完全一致，尤其在控制初始阶段，具有较大的偏差，可能会造成系统不稳定，因此在位置系统的输出时刻将所求得的角度θ当成给定的理想值作为内环姿态控制律的输入。为了保证系统的稳定性和跟踪误差的收敛性，在姿态子系统中设计控制的律时应当使其收敛速度大于位置子系统。

3 轮式移动机器人姿态控制律设计

通过位置控制律的设计实现了对位置方向的跟踪，并获得了满足给定位置点的跟踪角度θd，此时需要对系统的姿态也采用滑模控制算法实现θ跟踪到θd。

同样选取θ的跟踪误差θe=θ－θd，选取滑模函数为则有：

为了确保其误差收敛速度大于位置子系统，可以选取收敛速度较快的指数趋近律来设计，并采用饱和函数代替开关函数以减小滑模控制中产生的抖振现象。则可由此设计控制律为：

同样可根据李亚普洛夫方程验证系统是稳定的，姿态误差呈指数形式快速收敛为0。

4 仿真实验

为验证本文设计的正确性，本文在MATLAB 仿真软件下搭建了轮式移动机器人的仿真模型进行仿真验证。运行过程中给定相关的仿真参数如下。

位置指令[xd，yd]T=[t，sin（2x）+x+1]T，取控制器参数C1=C1=C1=0.1，k1=k2=0.2，k3=3，k4=2。移动机器人初始位置位于[0，0，0]。

仿真实验的目标是通过姿态控制器和位置控制器，使得移动机器人能够在短时间内从初始位置以最小的误差跟踪到给定的参考点，并能够保证稳定运行，图3、图4 给出了系统运行30 s 时间后，相应的被控对象的输出响应曲线。

图3 给出了移动机器人在仿真软件中的二维平面轨迹跟踪曲线，虚线代表期望的移动轨迹，实线代表机器人实际的运行轨迹。由图3 可以看出，在仿真开始阶段机器人运行轨迹同期望值存在偏差并在逐步缩小，到仿真进行至10 s之后，机器人运行轨迹同期望轨迹完全一致，说明系统能够满足控制要求。

图3 移动机器人在二维平面的轨迹跟踪仿真图

图4 给出了移动机器人在仿真软件中的x、y和θ的跟踪曲线，由图4 可以看出所设计的位置控制器和姿态控制器控制器能够快速准确地跟踪上两个位置方向和一个角度方向的自由移动轨迹，确保系统稳定运行。

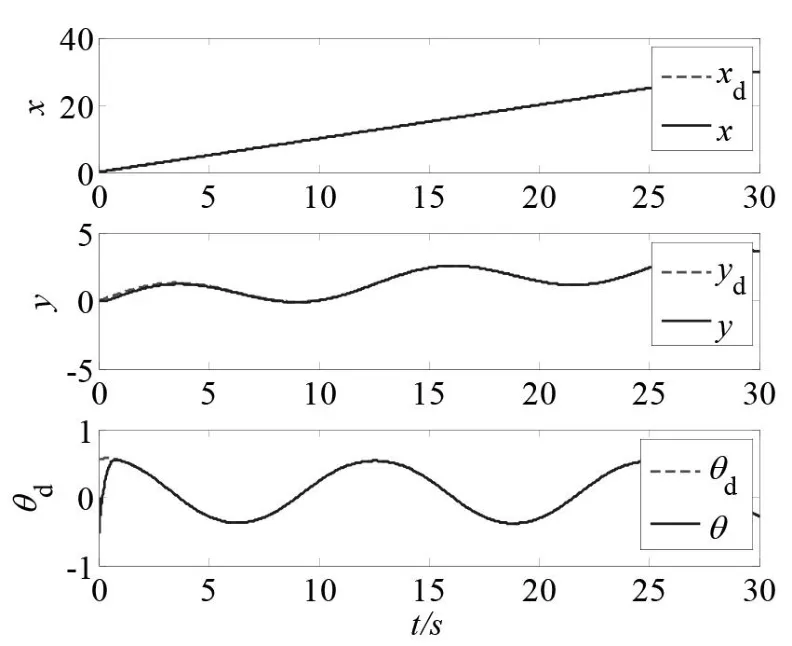
图4 移动机器人在位置和角度的轨迹跟踪仿真图

5 结论

本文针对轮式移动机器人轨迹跟踪系统，采用滑模控制技术，将被控系统分为姿态子系统和位置子系统的机构分别设计了相应的滑模控器，实现了轮式移动机器人在二维平面的轨迹跟踪控制，具有控制响应速度快、精确性高的特点。最后进行仿真实验，验证了设计的正确性和可靠性。